Синусоида вокруг нас

• Название: Синусоида вокруг нас
• Дата: 17.03.2023
• Размер: 0.6 Mb.
• Имя файла: Ministerstvo_obrazovanii_i_nauki_Permskogo_kraya.docx
• Тип: Реферат; #996987

Министерство образовании и науки Пермского края

Государственное бюджетное профессиональное образовательное учреждение

«Пермский колледж транспорта и сервиса»


ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по дисциплине____________________
ТЕМА «Синусоида вокруг нас»

Выполнил студент
Пирожников Игорь Андреевич

Группы СВ-21-1
Дата сдачи______________________
Руководитель:

Кондрякова Мария Александровна
Подпись________________________

г. Пермь,
2022г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 2

Глава 1. Основные понятия 3

1.1 Особенности построения 5

1.2 Тригонометрия в медицине 7

1.3 Тригонометрия в искусстве и архитектуре 10

1.4 Тригонометрия в астрономии 11

1.5 Тригонометрия в природе 13

ЗАКЛЮЧЕНИЕ 15

СПИСОК ЛИТЕРАТУРЫ 16

ВВЕДЕНИЕ

В данной работе я рассмотрю историю возникновения синусоида, изучу разные области, в которых используется тригонометрия. Данная работа будет полезна для учащихся старших классов, которые ещё не увидели всю красоту тригонометрии и не знакомы с областями её применения в окружающей жизни. Моя работа может расширить кругозор в области тригонометрии и ее использовании в разных областях нашей жизни. Ведь многие явления, происходящие в природе периодичны, а периодичность является одним из свойств тригонометрических функций. Такие явления можно наблюдать в биологии, в физике, медицине. Помимо периодичности она обладает вертикальной симметрией, а значит, тригонометрические функции имеют место и в практической деятельности – в архитектуре и искусстве. Для лучшего понимания материала, я использовал разные рисунки.

Актуальность темы «Синусоида вокруг нас»: развитие интереса к изучению темы «Тригонометрия» в курсе математики, расширение графических представлений.

Объект исследования: тригонометрические функции;

Предмет исследования: области их практического применения.

Цель: Раскрыть красоту и многообразие тригонометрии через явления окружающего мира, различные области деятельности человека

Задачи:

1. 
   изучить литературу по данной теме.
   
2. 
   выяснить, какие законы природы выражаются тригонометрической функцией.
   
3. 
   найти примеры применения тригонометрических функций в деятельности человека.
   
4. 
   проанализировать и систематизировать имеющийся материал.
   

Глава 1. Основные понятия

Синусоида — плоская кривая, задаваемая в прямоугольных координатах уравнением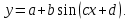



График уравнения [косинусоиды] вида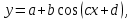



также зачастую называется синусоидой. Данный график получается из синусоидального сдвигом на 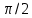в отрицательном направлении оси абсцисс. Термин «косинусоида» практически отсутствует в официальной литературе, поскольку является излишним.

В приведённых формулах a, b, c, d — постоянные;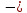

a характеризует сдвиг графика по оси Oy. Чем больше a, тем выше поднимается график;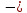

b характеризует растяжение графика по оси Oy. Чем больше увеличивается b, тем сильнее возрастает амплитуда колебаний;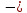

с характеризует растяжение графика по оси Ox. При увеличении c частота колебаний повышается ;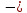

d характеризует сдвиг графика по оси Ox. При увеличении d график двигается в отрицательном направлении оси абсцисс.

Синусоидальное изменение какой-либо величины называется гармоническим колебанием. Примерами могут являться любые колебательные процессы начиная от качания маятника и кончая звуковыми волнами (гармонические колебания воздуха) — колебания напряжения в электрической сети переменного тока, изменение тока и напряжения в колебательном контуре и др. Также синусоида — проекция на плоскость винтовой линии, например, скрученного провода; рулон бумаги разрезанный наискось (косо усечённый цилиндр) и развернутый — край бумаги оказывается разрезанным по синусоиде.

1.1 Особенности построения

Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности (рис. 1):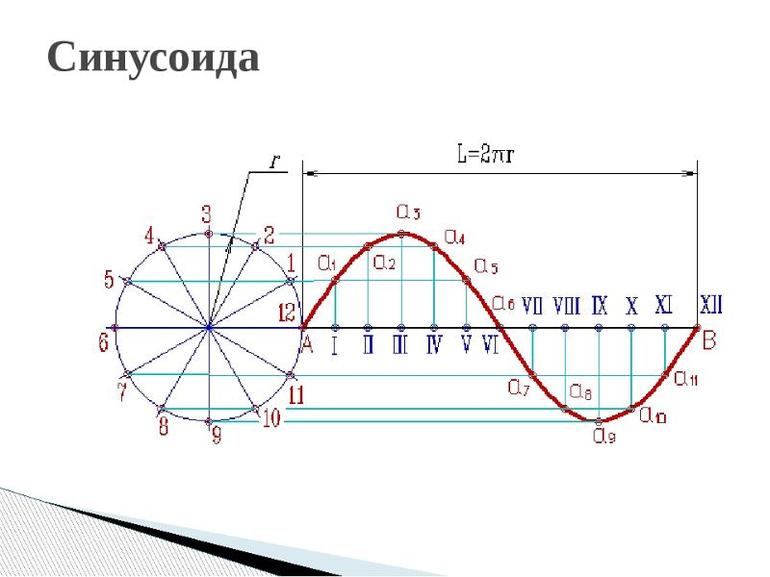



Рис. 1

• 
  проводится горизонтальная ось, на которой откладывается заданная длина волны;
  
• 
  отрезок делится на равные части;
  
• 
  слева чертится окружность с радиусом, равным величине амплитуды;
  
• 
  окружность делится на 12 одинаковых частей;
  
• 
  через полученные точки проводятся прямые;
  
• 
  из точек проводятся перпендикуляры к оси.
  

График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.

Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:

• 
  размах;
  
• 
  растяжение/сжатие;
  
• 
  фазовые колебания;
  
• 
  круговая частота.
  

При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:

• 
  А (а) — модуль неизвестной (расстояние от начала координат до точки А);
  
• 
  w — угловая частота;
  
• 
  t — время.
  

1.2 Тригонометрия в медицине

Человек со дня рождения находится в трех, биоритмах: физическом, эмоциональном и интеллектуальном.

Физический цикл равен 23 дням. Он определяет энергию человека, его силу, выносливость, координацию движения.

Эмоциональный цикл (28 дня) обусловливает состояние нервной системы и настроение.

Интеллектуальный цикл (33 дня) определяет творческую способность личности.

Любой из циклов состоит из двух полупериодов, положительного и отрицательного.

В течение первой половины физического цикла человек энергичен и достигает лучших результатов в своей деятельности; во второй половине цикла энергичность уступает лености.

В первой половине эмоционального цикла человек весел, агрессивен, оптимистичен, переоценивает свои возможности, во второй половине - раздражителен, легко возбудим, недооценивает свои возможности, пессимистичен, все критически анализирует.

Первая половина интеллектуального цикла характеризуется творческой активностью; во второй половине происходит творческий спад.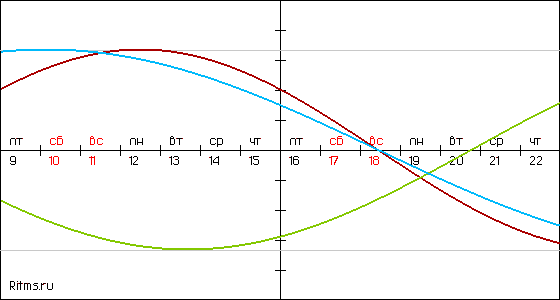



Рис. 2 Биоритмы

Модель биоритмов строят с помощью графиков тригонометрических функций. В интернете находится огромное количество сайтов, которые занимаются расчетом биоритмов. Для этого необходимо ввести дату рождения человека (день, месяц, год) и длительность прогноза.

В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрокардиографии.

Формула, получившая название тегеранской, представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, постановку диагноза и начало лечения .

На данный момент не известна точная информация касающегося вопроса, ведутся активные работы и исследования по данной теме.

Российские ученые вывели математическую формулу сердца. Благодаря этим уравнениям можно высчитать, спрогнозировать и предотвратить любое сердечное заболевание. Единственная в России лаборатория математической физиологии действует при Екатеринбургском Институте иммунологии и физиологии.

Проблема математических описаний физиологических функций организма – вторая по значимости проблема после проблемы ДНК человека. В будущем будут вычислены формулы других органов человека, и медики с помощью элементарных уравнений смогут прогнозировать и лечить любую болезнь.

Человек - сложнейший механизм, в котором непрерывно происходят физические и химические процессы. Если все процессы, перевести на язык уравнений, то можно будет вывести единую формулу человека.

Математики создали модель сердечной мышцы, которую биологи виртуально соединили с настоящей живой тканью. В компьютерной программе ученые задают сердцу различные нагрузки и наблюдают, как оно ведет себя. Изучив всевозможные алгоритмы, имитирующие деятельность сердца, ученые смогут делать реальные прогнозы.

Примененный в практических целях в 70-х годах 19 века англичанином А.Уоллером аппарат, записывающий электрическую активность сердца, электрокардиограмма, продолжает служить человеку и по сей день. Электрокардиограф позволяет выявить явные отклонения от нормального ритма сердца, такие как Инфаркт миокарда, Ийшемическая болезнь сердца, синусовая брадикардия, тахекардия,аритмия, синдром слабости синусового узла и т.п.

1.3 Тригонометрия в искусстве и архитектуре

С того времени как человек стал существовать на земле, основой улучшения быта и других сфер жизни стала наука. Основы всего, что создано человеком – это различные направления в естественных и математических науках. Одна из них – геометрия. Архитектура не единственная сфера науки, в которой используются тригонометрические формулы. Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Рассмотрим пример на построение одной скульптуры французского мастера Золотого века искусства.

Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу. Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы, тем самым найдем точку зрения.

Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий: Детская школа Гауди в Барселоне, Небоскрёб Мэри-Экс в Лондоне, Винодельня «Бодегас Исиос» в Испании,Ресторан в Лос-Манантиалесе в Аргентине. При проектировании этих зданий не обошлось без тригонометрии.

1.4 Тригонометрия в астрономии

Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры. Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно вычислению значения sin угла 3. По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны; на самом деле Солнце почти в 400 раз дальше, чем Луна, ошибка возникла из-за неточности в измерении угла.

Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.

В общем, можно сказать, что тригонометрия использовалась для:

• 
  точного определения времени суток;
  
• 
  вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;
  
• 
  нахождения географических координат текущего места;
  
• 
  вычисления расстояния между городами с известными географическими координатами.
  

1.5 Тригонометрия в природе

Тригонометрия встречается и в природе. При полёте птицы траектория взмаха крыльев образует синусоиду (рис. 3)





Рис. 3 Траектория взмаха крыльев птицы

Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.

Северное сияние, всеми знакомое нам явление, также связано с синусоидальным законом:

Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

Сила, действующая на движущуюся в магнитном поле заряженную частицу, называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.

Поворот на 360° вокруг Солнца Земля совершает за 365 дней. Движение Земли вокруг Солнца иллюстрирует «движение» точки тригонометрической окружности (рис. 4)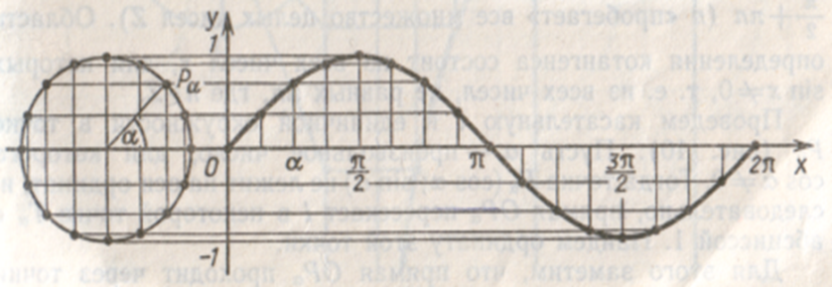



Рис. 4 «Движение» точки тригонометрической окружности

ЗАКЛЮЧЕНИЕ

Изучив тему своей работы, я понял, что данная отрасль тесно связана со многими науками.

Тригонометрия тесно связана с физикой, встречается в природе, архитектуре, медицине, биологии, и строительстве.

Тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться, поэтому знание её законов необходимо каждому.

Благодаря этой области был изобретен Электрокардиограф позволяющий выявить явные отклонения от нормального ритма сердца. Данное открытие помогает врачам выполнять более квалифицированно и качественно медицинскую помощь.

Отметим также, что , знакомясь с ее влиянием в других областях, мы можем сделать вывод о том, что тригонометрия активно влияет на жизнедеятельность человека

Цель моего проекта выполнена успешна.

СПИСОК ЛИТЕРАТУРЫ

1. 
   Алимов Ш.А.и др. "Алгебра и начала анализа" Учебник для 10-11 классов общеобразовательных учреждений, М., Просвещение, 2010.
   
2. 
   Виленкин Н.Я. Функции в природе и техники: Кн. для внеклас. чтения IX-XX кл. – 2-е изд., испр. - М: Просвещение, 1985.
   
3. 
   История математики с Древнейших времен до начала XIX столетия в 3-х томах// под ред. А. П. Юшкевича. Москва, 1970г. – том 1-3 Э. Т. Бэлл Творцы математики.
   
4. 
   Маслова Т.Н. «Справочник школьника по математике»
   
5. 
   Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.