отчет. Систем управления и радиоэлектроники

• Название: Систем управления и радиоэлектроники
• Дата: 14.05.2023
• Размер: 82.57 Kb.
• Имя файла: отчет.docx
• Тип: Отчет; #1128742

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР)

Кафедра компьютерных систем в управлении и проектировании
(КСУП)


Отчёт по контрольной работе № 1

по дисциплине

«Искусственный интеллект»

Вариант 3

Томск – 2021

1. 
   Напишите предикат p(+L, -S) - истинный тогда и только тогда, когда L - список списков, а S
   

- список, объединяющий все эти списки в один.
% на входе список списков - на выходе результат их конкатенации p(L, S):-

% если на входе пустой список - вернем пустой список L = [], !, S = [];

% если на входе список из одного элемента - вернем его значение

% потому что для [[1,2,3]] надо вернуть [1,2,3] L = [H], !, S = H;

% если на входе список из двух элементов - то соединяю их

% для соединения использую функцию append (встроенную)

% потому что для [[1,2,3],[4,5,6]] надо вернуть [1,2,3,4,5,6] L = [First, Second], !, append(First, Second, S);

% иначе - в списке более двух элементов

% запомним первый элемент (head), а остальные - обработаем рекурсивно

% в итоге получится TailResult, к нему остается добавить Head

% добавить можно с помощью того же append L = [Head|Tail], !, p(Tail, TailResult), append(Head, TailResult, S).
% таким образом, список из трех элементов будет обработан так:

%% последнее правило отделит от него первый элемент

%% остальные обработает рекурсивно

%%% рекурсивный вызов произойдет над списком из двух элементов

%%% поэтому ответ будет найден по предпоследнему правилу

%% ответ вернется в правило над тремя элементами, там к нему

%% "приделается" первый элемент
% если элементов больше (N) - работает также,

% но последнее правило вызовется N-2 раза...

/**

?- p([[1,2,3]], S).

?- p([[1,2,3],[4,5,6],[8],[1,2]], S).

?- p([[1,2,3],[4,5,6]], S).

*/

2. 
   Напишите предикат p(+L, -S) - истинный тогда и только тогда, когда список S есть циклическая перестановка элементов списка L, например, p([f, g, h, j], [g, h, j, f]) -истина.
   

% надо проверить является ли S циклической

% перестановкой элементов списка L

% например... L = [1,2,3,4,5,6,7]

% если S = [5,6,7,1,2,3,4] - то является

% если же S = [5,6,7,1,2,4,3] - то НЕ является
% несложно заметить, что циклические перестановки получаются

% путем разбиения L на два подсписка, которые слепляются в ином порядке

% убедиться в этом можно просто попереберав

% по очереди циклические перестановки... например для L:

% S = [7, 1,2,3,4,5,6]

% S = [6,7, 1,2,3,4,5]

% S = [5,6,7, 1,2,3,4]

% S = [4,5,6,7, 1,2,3]

% ...
% то-есть правило такое...

% если список L можно разбить на два подсписка (A и B)

% так, что при их соединении в порядке (B + A) получится S

% то S является перестановкой L
% разбить на подсписки можно все тем же append, который использовался

% в предыдущей работе для соединения списков

% вызов

% ?- append(-A, -B, +L)

% разобьет список L на все возможные подсписки

% вызов

% ?- append(+B, +A, -S)

% соединит списки B + A p(L, S):-

append(A, B, L),

append(B, A, S), !.

/**

?- p([1,2,3],[3,2,1]).

?- p([1,2,3,4,5,6,7],[5,6,7,1,2,3,4]).

*/

3. 
   Напишите предикат p(+L, -N) - истинный тогда и только тогда, когда N - количество различных элементов списка L.
   

% чтобы посчитать количество различных элементов

% в списке можно поступить по-разному...

%

% например, можно удалить все повторяющиеся элементы,

% а потом определить длину.

% Это удобно, ведь для определения

% длины есть встроенный предикат length

% ?- length([1,2,3], X). % X = 3

%

% можно каждым элементом делить список на правую и левую части

% например для [1,2,3,4,5,6] число 3 делит список на

% [1,2] и [4,5,6]

% чтобы посчитать каждое число всего один раз - счетчик надо

% увеличивать если числа нет в левой части

% (такое число раньше не встречалось)

%

% реализуется второй вариант, так как первый сложен

% ведь удалить повторы из списка не проще чем решить исходную задачу
% основной предикат будет вызывать вспомогательный, который

% принимает дополнительным аргументом "левую" часть списка

% изначально она пустая, ведь никакие элементы еще не обработаны p(L, N):-

helper(L, [], N).
helper(L, LeftPart, N):-

% если исходный список пуст - вернуть надо ноль, это просто L = [], !, N is 0;

% иначе разделяем список на первый и остальные элементы

% и ищем элемент в левой части. если он там есть то

% ... то member(Head, LeftPart) завершится успешно

% тогда счетчик увеличивать не нужно, элемент уже был посчитан

% значит вызываем функцию рекурсивно,

% полученный (от вызова) результат вернем без изменений

% еще стоит обратить внимание, что при выполнении рекурсивного вызова

% надо добавить Head к левой части,

% ведь обработанный элемент должен туда попадать L = [Head|Tail],

member(Head, LeftPart), !, helper(Tail, [Head|LeftPart], N);

% иначе - попадаем в последнее правило.

% мы никак не попадем сюда если список пуст

% или Head встретился в LeftPart, так как в правила выше расставлены

% отчечения (оператор "!").

% поэтому тут проверку на счет того, встречается элмент или нет

% можно не делать.

% итак... мы сюда попали потому что элемент Head не был посчитан ранее

% значит надо выполнить рекурсивный вызов (как выше) и к полученному результату

% добавить единицу L = [Head|Tail],

helper(Tail, [Head|LeftPart], TailN), N is TailN + 1.
/**

?- p([1,2,3,4,5,6,7], N).

?- p([1,2,3,4,3,2,1], N).

*/

4. 
   Напишите предикат p(+X, +Y, -Z) - истинный тогда и только тогда, когда Z есть "пересечение" списков X и Y, т.е. список, содержащий их общие элементы, причем кратность каждого элемента в списке Z равняется миимуму из его кратностей в списках X и Y.
   

Решение:

На входе 2 списка (X, Y) - на входе результат их пересечения (Z) под пересечением имеется ввиду что-то похожее на пересечение множеств, но элементы в исходных списках и результирующем могут дублироваться. Причем


Алгоритм может быть таким:

1. 
   перебираем элементы (E) списка X
   
2. 
   
   % member(E, X), member(E, Y)
   для каждого из них проверяем принадлежность списку Y Перебрать и проверить принадлежность можно с помощью member: в итоге мы получим элементы, принадлежащие обоим спискам.
   
3. 
   для каждого E определить сколько раз он входит в X, сколько в Y и столько раз добавить его в Z.
   

Однако, оказывается, что этого мало. Приведенный выше фрагмент первых двух пунктов работает не так как хотелось бы если элементы в списках повторяются: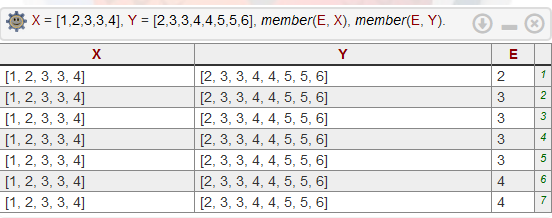





Каждый элемент E будет перебран столько раз: count(Zi, X) * count(Zi, Y)

Поэтому число 3 в этом примере возвращается 4 раза. Поэтому дополнительно надо учитывать "был ли этот элемент обработан ранее".
Чтобы посчитать сколько раз элемент входит в список был написан такой предикат:


% если список пустой - то вернуть 0 для любого E count([], _E, 0):-!.

% разделить список на H и Tail, если H = E - то:

% Tail Обрабатываем рекурсивно, а к полученному результату добавляем единицу count([H|Tail], E, Count):-

H = E, !, count(Tail, E, CountTail), Count is CountTail + 1;

% иначе - просто обрабатываем Tail и полученному результату ничего не добавляем count(Tail, E, Count).



Также, понадобится вспомогательный предикат для добавления элемента в список N

раз.
Для реализации описанного выше алгоритма надо хранить "уже обработанные" элементы, для этого можно использовать дополнительный аргумент функции. При этом оказывается неудобным показанный выше способ перебора элементов с помощью member.

Основная функция вызывает вспомогательную, передавая туда пустой список в качестве значения этого аргумента, так как в начальный момент никакие элементы еще не обработаны:



Функция helper перебирает элементы списка X по очереди: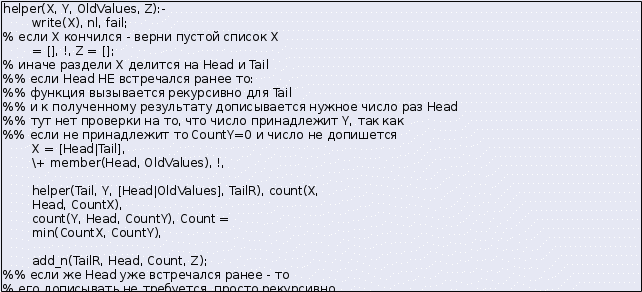



Исходный код программы целиком:

5. 
   Определите отношение ordered(+Tree), выполненное, если дерево Tree является упорядоченным деревом целых чисел, т. е. число, стоящее в любой вершине дерева, больше любого элемента в левом поддереве и меньше любого элемента в правом поддереве. Указание. Можно использовать вспомогательные предикаты ordered_left(+X, +Tree) и ordered_right(+X, +Tree), которые проверяют, что X меньше (больше) всех чисел в вершинах левого (правого) поддерева дерева Tree и дерево Tree - упорядочено.
   

Решение:


% проверяет что число X меньше всех элементов в Tree ordered_left(X, Tree):-

% если дерево пустое - то умловие выполнено Tree = empty, !;

% иначе проверяем что X больше корня

% и всех элементов справа и слева (рекурсивно) Tree = tree(Root, Left, Right),

X > Root, ordered_left(X, Left), ordered_left(X, Right).
% проверяет что число X больше всех элементов в Tree

% работает точно как ordered_left но оператор сравнения другой ordered_right(X, Tree):-

Tree = empty, !;

Tree = tree(Root, Left, Right), X < Root,

ordered_right(X, Left), ordered_right(X, Right).
ordered(Tree):-

%

Tree = empty, !;

% тут для правого поддерева применяется right,

% а для левого left

Tree = tree(Root, Left, Right), ordered_right(Root, Right), ordered_left(Root, Left), !.




Для тестирования были описаны такие деревья: 1)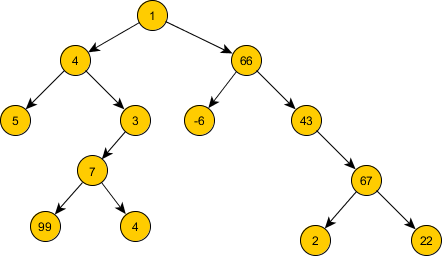




?- Tree = tree(1, tree(4,

tree(5, empty, empty), tree(3,

tree(7,

tree(99, empty, empty), tree(4, empty, empty)

),

empty

)

),

tree(66,

tree(-6, empty, empty), tree(43,

empty, tree(67,

tree(2, empty, empty), tree(22, empty, empty)

)

)

)

),

ordered(Tree).



Это дерево не упорядочено - это очевидно.

2)


?- Tree = tree(1, tree(-5,

tree(-6, empty, empty), tree(3,

tree(-3, empty,

tree(-33, empty, empty), tree(0, empty, empty)

),

empty

)

),

tree(20,

tree(10, empty, empty), tree(43,

empty, tree(67,

tree(45, empty, empty), tree(88, empty, empty)

)

)

)

),

ordered(Tree).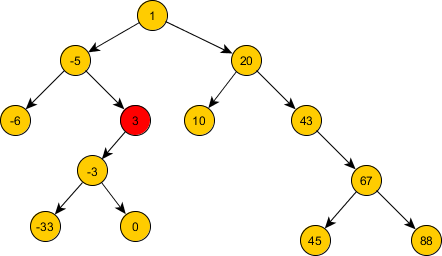


На первом ярусе все упорядочено. И на втором, казалось бы - тоже. Но число 3 находится в левом поддереве числа 1 поэтому должно быть меньше 1. При его замене на число -4 возникнет неупорядоченность числа 0 (ведь ноль находится в левом поддереве числа -4).

Упорядоченное дерево:



Исходный код программы с тестами целиком:

% проверяет что число X меньше всех элементов в Tree ordered_left(X, Tree):-

% если дерево пустое - то умловие выполнено Tree = empty, !;

% иначе проверяем что X больше корня

% и всех элементов справа и слева (рекурсивно) Tree = tree(Root, Left, Right),

X > Root, ordered_left(X, Left), ordered_left(X, Right).
% проверяет что число X больше всех элементов в Tree

% работает точно как ordered_left но оператор сравнения другой ordered_right(X, Tree):-

Tree = empty, !;

Tree = tree(Root, Left, Right), X < Root,

ordered_right(X, Left), ordered_right(X, Right).
ordered(Tree):-

%

Tree = empty, !;

% тут для правого поддерева применяется right,

% а для левого left

Tree = tree(Root, Left, Right), ordered_right(Root, Right), ordered_left(Root, Left), !.

/**

?- Tree = tree(1, tree(4,

tree(5, empty, empty), tree(3,

tree(7,

tree(99, empty, empty), tree(4, empty, empty)

),

empty

)

),

tree(66,

tree(-6, empty, empty), tree(43,

empty, tree(67,

tree(2, empty, empty), tree(22, empty, empty)

)

)

)

),

ordered(Tree).

?- Tree = tree(1, tree(-5,

tree(-6, empty, empty), tree(3,

tree(-3, empty,

tree(-33, empty, empty), tree(0, empty, empty)

),

empty

)

),

tree(20,

tree(10, empty, empty), tree(43,

empty, tree(67,

tree(45, empty, empty), tree(88, empty, empty)

)

)

)

),

ordered(Tree).

?- Tree = tree(1, tree(-5,