теория-билеты экзамен по информатике. Система счисления это совокупность приемов и правил, по которым числа записываются и читаются
 Скачать 144.81 Kb. Скачать 144.81 Kb.
|
|
| Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10—1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.
Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q сводится к вычислению значения многочлена
x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-m q-m
средствами десятичной арифметики.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:
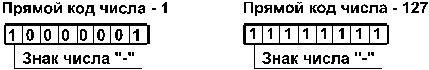
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Билет № 2 (так же 25 и 40)
Типы данных. Переменные. Байтовые, целые, числа с плавающей запятой. Структура этих типов.
Тип данных – это множество допустимых значений, которые может принимать тот или иной объект, а также множество допустимых операций, которые применимы к нему. В современном понимании тип также зависит от внутреннего представления информации.
Тип данных определяет:
внутреннее представление данных в памяти компьютера;
объем памяти, выделяемый под данные;
множество (диапазон) значений, которые могут принимать величины этого типа;
операции и функции, которые можно применять к данным этого типа.
Основные типы данных в C++
int — целочисленный тип данных
float — тип данных с плавающей запятой
double — тип данных с плавающей запятой двойной точности
char — символьный тип данных - значениями являются различные символы из кодовой таблицы, например: 'ф', ':', 'j' (при записи в программе они заключаются в одинарные кавычки).
bool — логический тип данных (1 байт)
| Тип | Размер в байтах (битах) | Интервал изменения |
| char | 1 (8) | от -128 до 127 |
| unsigned char | 1 (8) | от 0 до 255 |
| signed char | 1 (8) | от -128 до 127 |
| int | 2 (16) | от -32768 до 32767 |
| unsigned int | 2 (16) | от 0 до 65535 |
| signed int | 2 (16) | от -32768 до 32767 |
| short int | 2 (16) | от -32768 до 32767 |
| unsigned short int | 2 (16) | от 0 до 65535 |
| signed short int | 2 (16) | от -32768 до 32767 |
| long int | 4 (32) | от -2147483648 до 2147483647 |
| unsigned long int | 4 (32) | от 0 до 4294967295 |
| signed long int | 4 (32) | от -2147483648 до 2147483647 |
| float | 4 (32) | от 3.4Е-38 до 3.4Е+38 |
| double | 8 (64) | от 1.7Е-308 до 1.7Е+308 |
| long double | 10 (80) | от 3.4Е-4932 до 3.4Е+4932 |
Те элементы данных, которые сохраняют неизменные значения на протяжении всего времени работы программы, принято называть константами
Другие же объекты, являющиеся предметом изменения в ходе выполнения алгоритма, называют переменными
Переменная – определенный именованный участок памяти, имеющий свое имя, тип и адрес.
При определении переменной должны быть заданы тип данных, имя переменной и, возможно, начальное значение.
Структура типов данных с плавающей запятой
Число с плавающей запятой состоит из:
Знака (указывающего на отрицательность или положительность числа)
Мантиссы (выражающей значение числа без учёта порядка)
Порядка (экспоненты) (степень основания числа, на которое умножается мантисса)
Представление числа в нормализованном экспоненциальном виде.
Возьмем, к примеру, десятичное число 155,625.
155,62510 = 10011011,1012 - число в десятичной и в двоичной системе
Приведем полученное число к нормализованному виду в десятичной и двоичной системе:
1,55625∙exp10+2= 1,0011011101∙exp2+111
В результате мы получили основные составляющие экспоненциального нормализованного двоичного числа:
Мантиссу M=1,0011011101
Экспоненту exp2= +111
Переменной типа float компилятор отводит 4 байта памяти.
Eе численное значение хранится в нормализованном виде. Нормализация состоит в сдвиге значащих бит двоичного кода числа влево или вправо до тех пор, пока целая часть числа не станет равной единице. Разумеется, для сохранения численного значения каждая операция сдвига сопровождается соответствующим изменением двоичного порядка числа
Но если целая часть нормализованного двоичного числа всегда равна единице, ее можно вообще не хранить в ячейке памяти, это экономит один "лишний" бит для записи мантиссы, увеличивая точность представления чисел. При чтении числа из ячейки памяти такая "неявная единица", автоматически восстанавливается.

Билет 3,24,39
Операции и выражения. Перечисляемые константы. Преобразования типов (явные, неявные). Приоритеты и порядок выполнения.
А) Операции и выражения.
Во всех языках программирования под выражением подразумевается конструкция, составленная из констант, переменных, знаков операций, функций, скобок. Выражение определяет порядок вычисления некоторого значения. Если это числовое значение, то такое выражение называют арифметическим. Вот несколько примеров арифметических выражений, записанных по правилам языка Си:
a+b 12.5-z 2*(X+Y)
Эти выражения имеют традиционную форму для языков программирования высокого уровня, поэтому их смысл очевиден.
Опишем набор операций, используемых в Си, а также правила записи и вычисления выражений.
Арифметические операции. К арифметическим операциям относятся:
— вычитание;
+ сложение;
* умножение;
/ деление;
% деление по модулю;
Все операции, кроме деления по модулю, применимы к любым числовым типам данных. Операция % применима только к целым числам.
Б) Перечисляемые константы.
В Си для представления константы рекомендуется использовать объявление переменной с начальным значением и ключевым словом const:
const тип ИмяПеременной = НачальноеЗначение;
const int n=10;
Область видимости константы такая же, как у обычной переменной. С помощью ключевого слова const можно объявить указатель на константу:
const тип *ИмяПеременной;
const int *m; // m – указатель на константу типа int
const int n=3;
m = &n;
Еще одна возможность const состоит в создании постоянного указателя на величину указанного типа
тип *const ИмяПеременной = Значение;
int i;
int *const ptri=&i;
В) Преобразования типов (явные, неявные).
В Си различают явное и неявное преобразование типов данных. Неявное преобразование типов данных выполняет компилятор Си, ну а явное преобразование данных выполняет сам программист. Явные преобразования могут приводить к потере точности (из int в byte). При неявных преобразованиях результат всегда успешен и не приводит к потере точности данных, выполняются автоматически (float в double или byte в int).
Пример неявного преобразования:
В качестве целочисленного типа данных возьмем int, ну и вещественный тип данных у нас будет float.
| x | y | Результат деления | Пример |
| делимое | делитель | частное | x = 15 y = 2 |
| int | int | int | 15/2=7 |
| int | float | float | 15/2=7.5 |
| float | int | float | 15/2=7.5 |
Из таблицы видно, что меняя переменные различных типов данных местами, результат остается тот же.
Пример явного преобразования:
Что же касается явного преобразования, то оно необходимо для того чтобы выполнять некоторые манипуляции, тем самым меняя результат вычисления. Самый простой способ явного преобразования типов данных, пример: допустим нам необходимо разделить такие числа 15 и 2, делим. 15/2=7. Результат тот же, что и в таблице. Но если сделать незначительные преобразования, например: 15.0/2=7.5 при таком делении число 15 является вещественным, значит и результат будет вещественный. Само число 15 с точки зрения математики не изменилось, ведь 15=15.0.
Г) Приоритеты и порядок выполнения.
Приоритет и ассоциативность операций в языке Си
| Знак операции | Наименование | Ассоциативность |
| 1.() [] . -> | Первичные | Слева направо |
| 2.+ - ! * & ++ -- sizeof приведение типа | Унарные | Справа налево |
| 3.* / % | Мультипликативные | Слева направо |
| 4.+ - | Аддитивные | Слева направо |
| 5.>> << | Сдвиг | Слева направо |
| 6.< > <= >= | Отношение | Слева направо |
| 7.== != | Отношение | Слева направо |
| 8.& | Поразрядное И | Слева направо |
| 9.^ | Поразрядное исключающее ИЛИ | Слева направо |
| 10. | | Поразрядное включающее ИЛИ | Слева направо |
| 11. && | Логическое И | Слева направо |
| 12. || | Логическое ИЛИ | Слева направо |
| 13. ?: | Условная | Справа налево |
| 14. = *= /= %= += -= <<= >>= &= |= ^= | Простое и составное присваивание | Справа налево |
| 15. , | Последовательное вычисление | Слева направо |
Из таблицы следует, что операнды, представляющие вызов функции, индексное выражение, выражение выбора элемента и выражение в скобках, имеют наибольший приоритет и ассоциативность слева направо. Приведение типа имеет тот же приоритет и порядок выполнения, что и унарные операции.
Выражение может содержать несколько операций одного приоритета. Когда несколько операций одного и того же уровня приоритета появляются в выражении, то они применяются в соответствии с их ассоциативностью — либо справа налево, либо слева направо.
Билет 4, 23, 38
Операторы языка. Составной оператор. Управляющие конструкции языка.
Операторы языка C++
Операторы управляют процессом выполнения программы. Набор операторов языка С++ содержит все управляющие конструкции структурного программирования.
Составной оператор ограничивается фигурными скобками. Все другие операторы заканчиваются точкой с запятой.
Пустой оператор – ;
Пустой оператор – это оператор, состоящий только из точки с запятой. Он может появиться в любом месте программы, где по синтаксису требуется оператор. Выполнение пустого оператора не меняет состояния программы.
Составной оператор – {...}
Действие составного оператора состоит в последовательном выполнении содержащихся в нем операторов, за исключением тех случаев, когда какой-либо оператор явно передает управление в другое место программы
Управляющие конструкции языка C/C++.
Функции, их прототипы и реализация
