лекцыия 4. Лекция 4. Системы линейных алгебраических уравнений. N мерные векторы
 Скачать 250.5 Kb. Скачать 250.5 Kb.
|
|
Системы линейных алгебраических уравнений. N- мерные векторы. Определение 1. Всякая упорядоченная совокупность из nчисел Два n- мерных вектора равны, если равны их соответствующие компоненты. Вектор Над векторами вводятся следующие операции: 1. Сложение векторов 2. Умножение векторов на число Определение 2. Система векторов иначе система - линейно независимая. Пример 1. Вектора Векторы Линейная зависимость системы векторов означает, что хотя бы один из векторов системы можно выразить линейной комбинацией остальных. Пусть Q произвольная система векторов. Определение 3. Система Формула (1) называется разложением вектора Теорема 1. Любая система из Определение 4. Рангом системы векторов называется число векторов в базисе этой системы и оно равно максимально возможному количеству линейно независимых векторов этой системы. Теорема 2. Ранг системы векторов равен рангу матрицы, строки которой состоят из компонентов векторов этой системы. Определение 5. Множество Ранг пространства 2. Системы линейных алгебраических уравнений. Методы решения. Определения. 6. Системой  (2) (2)где 7. Числа 8. Систему (2) назовем совместной, если она имеет хотя бы одно решение, и, несовместной – в противном случае. 9. Совместную систему (2) назовем определенной, если она имеет единственное решение, иначе – неопределенной. 10. Если Из примера 9 (лекция 1) следует, что систему (1) можно записать в матричном виде  Теорема Кронекера-Капелли. Для того, что бы система (2) была совместной, необходимо и достаточно, чтобы  расширенная матрица системы (2). Так как каждое уравнение системы (2) однозначно определяется набором коэффициентов этого уравнения, то рассматривая строки матрицы Следствие 1. Система (2) является определенной тогда и только тогда, когда где Рассмотрим случай, когда Правило Крамера. Решение системы (2) определяется формулами где 2. Матричный способ. Так как 3. Метод Гаусса (метод исключения неизвестных). С помощью элемен-тарных преобразований систему (2) приводят к эквивалентной ей системе  (3) (3)из которой затем находят неизвестные. Пример 2. Рассмотренными способами решить систему уравнений. 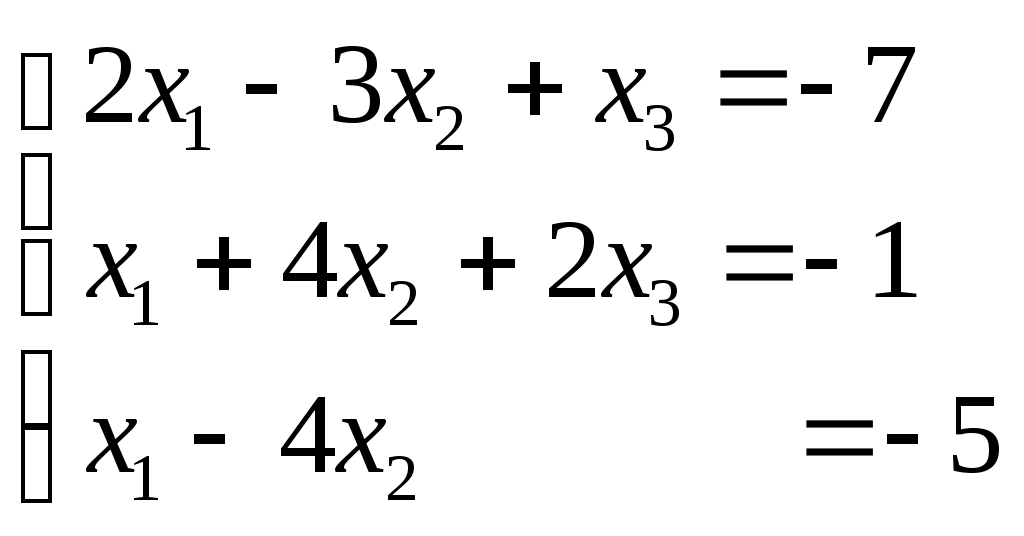 (4) (4)Решение. 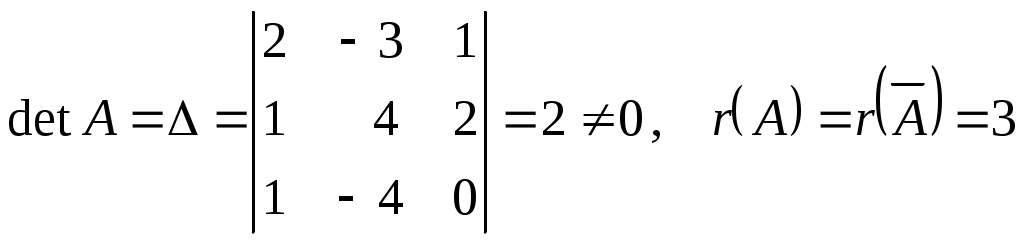 Следовательно система (4) имеет единственное решение. а) Правило Крамера. Найдем 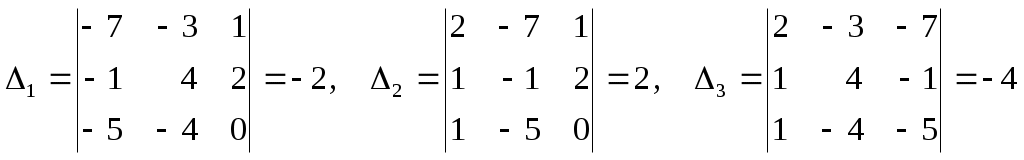 . .Отсюда б) Матричный способ. Запишем систему (4) в виде 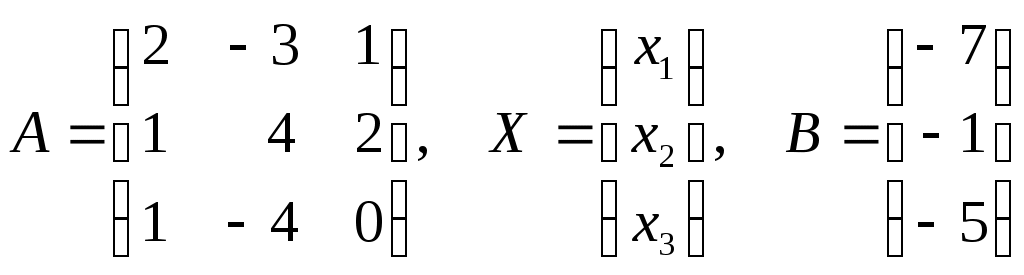 . .Из примера 10 (лекция 1) имеем 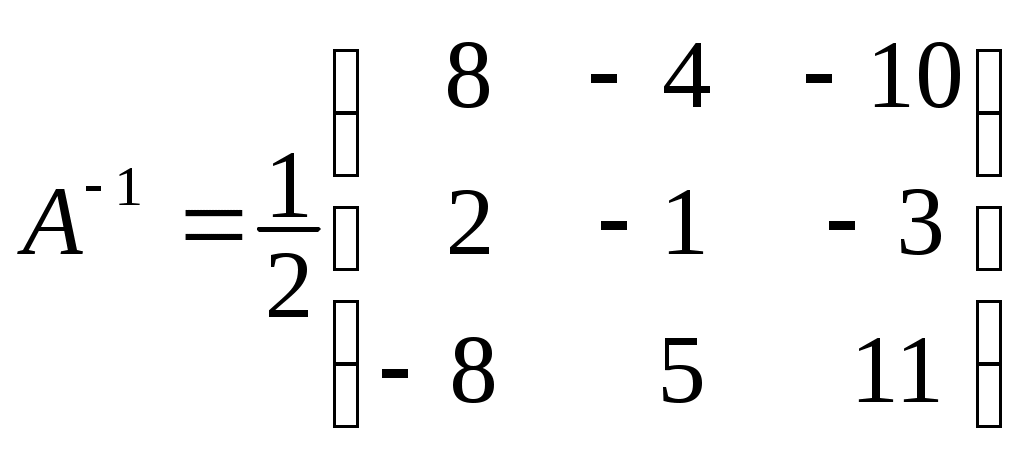 . .Следовательно из 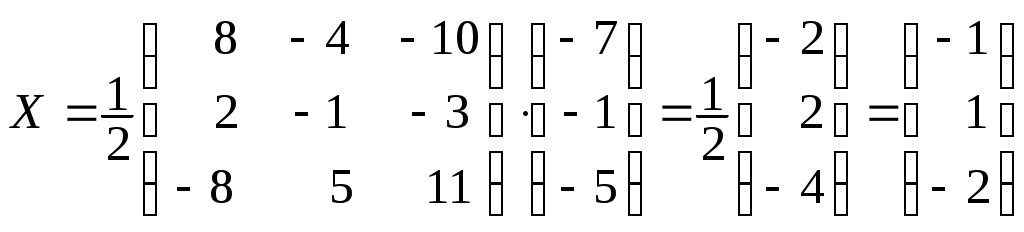 или 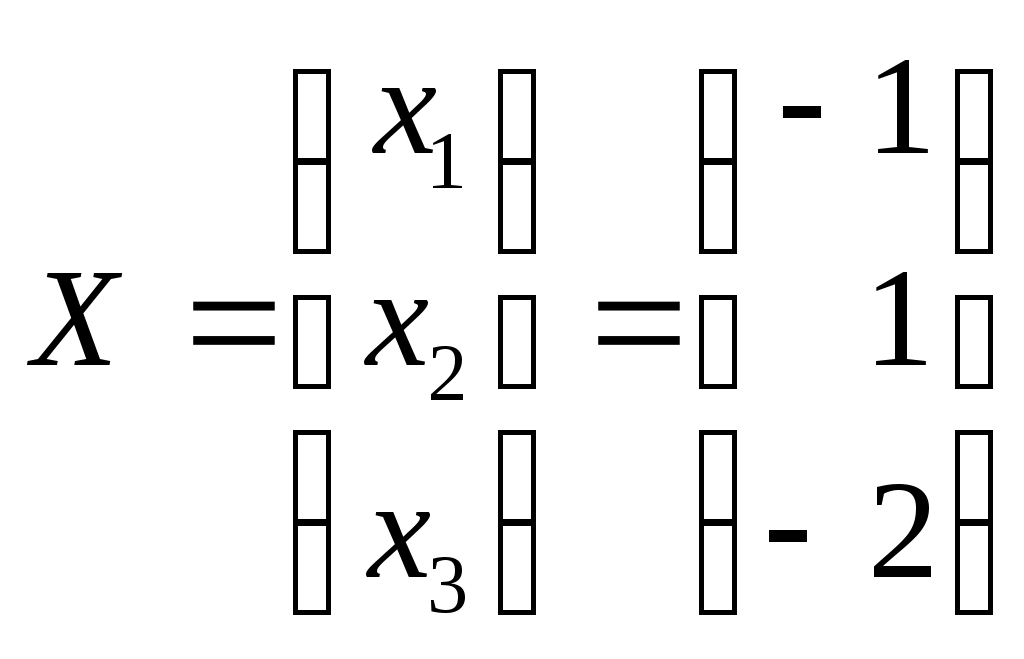 . .Отсюда в) Метод Гаусса. Переставим местами 1-е и 2-е уравнения 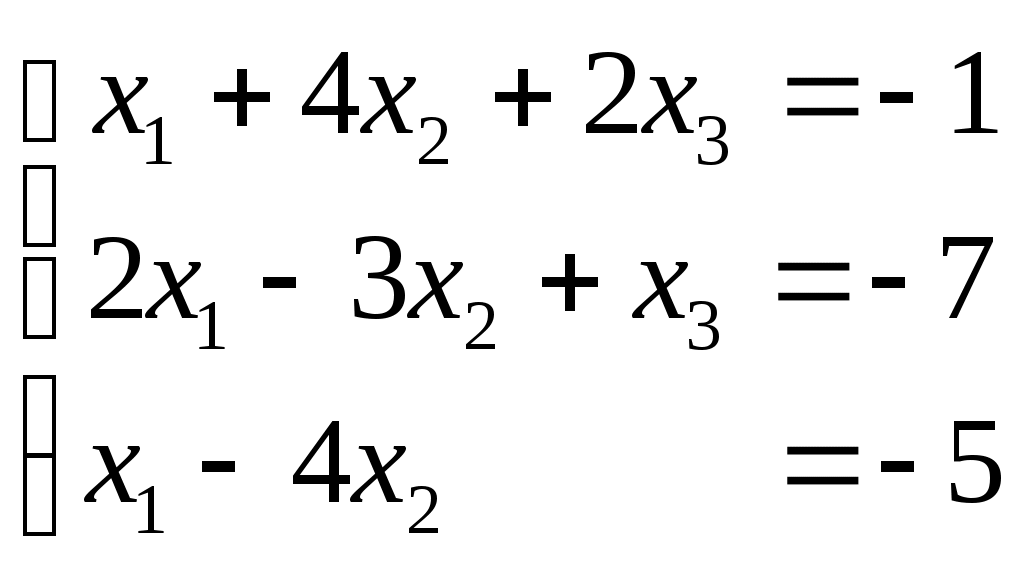 Умножим 1-е уравнение на –2 и сложим его 2-м уравнением. Затем, умножим 1-е уравнение на –1 и сложим его с 3-м уравнением. Таким образом мы исключим 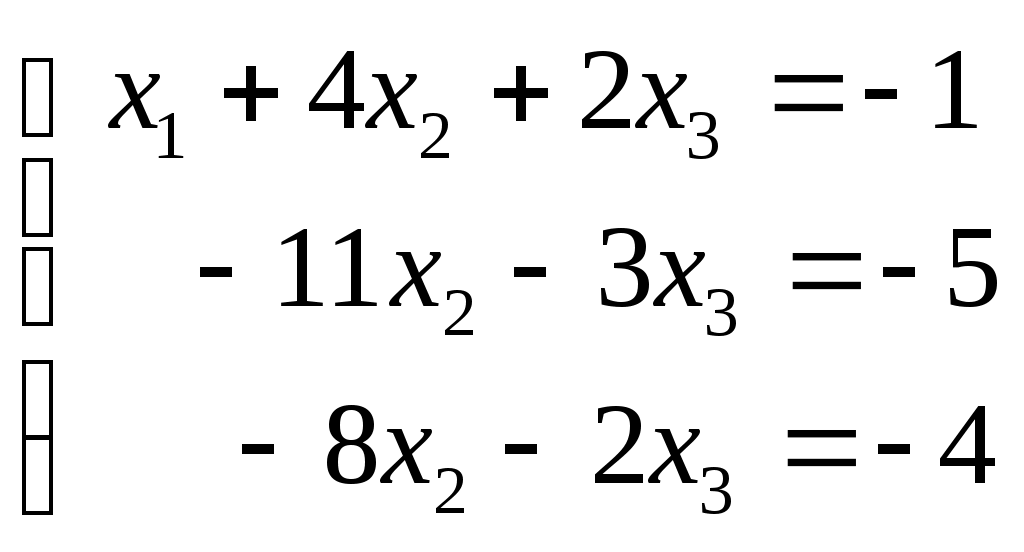 Умножим 2-е уравнение на 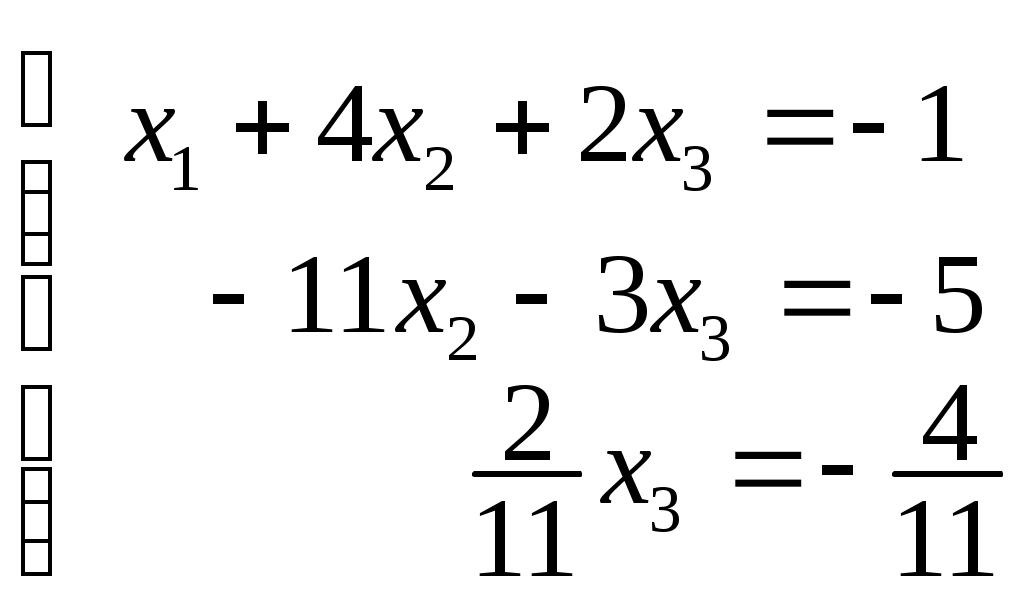 Из 3-го уравнения 2.1. Понятие общего решения Рассмотрим общий случай, когда количество уравнений может не совпадать с количеством неизвестных и Не снижая общности, можно считать, что 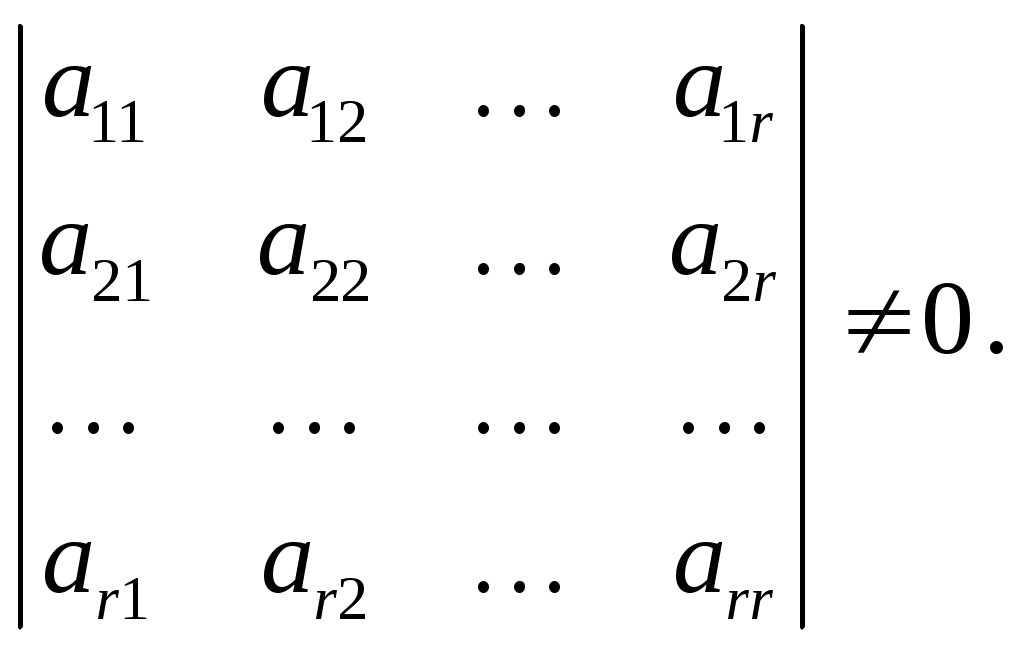 (5) (5)Из (5) следует, что последние 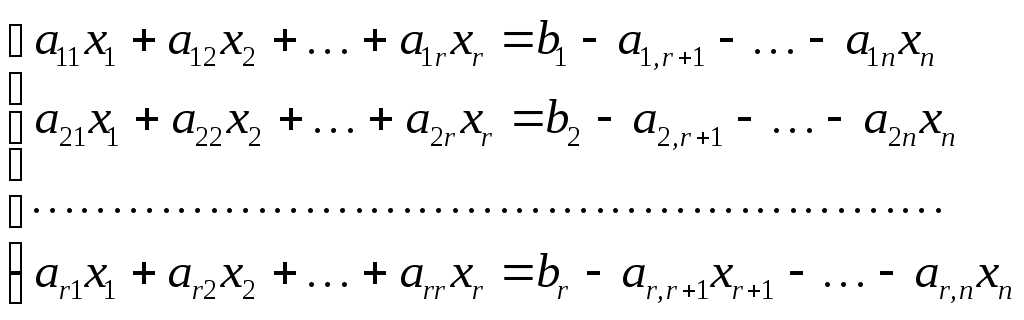 (6) (6)Переменные Пример 2. Установить совместность и найти общее решение системы 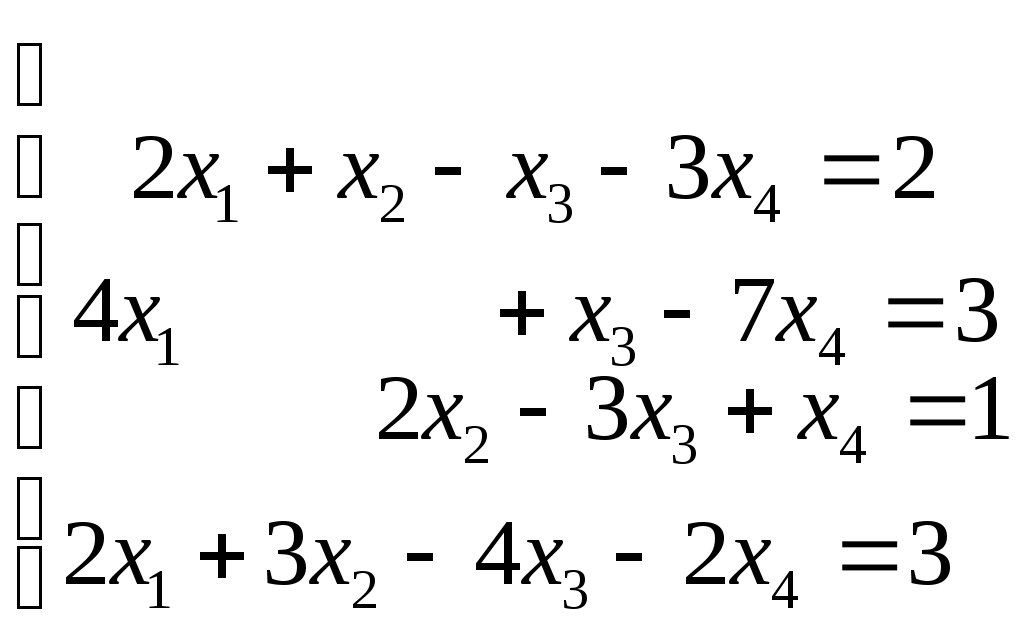 (7) (7)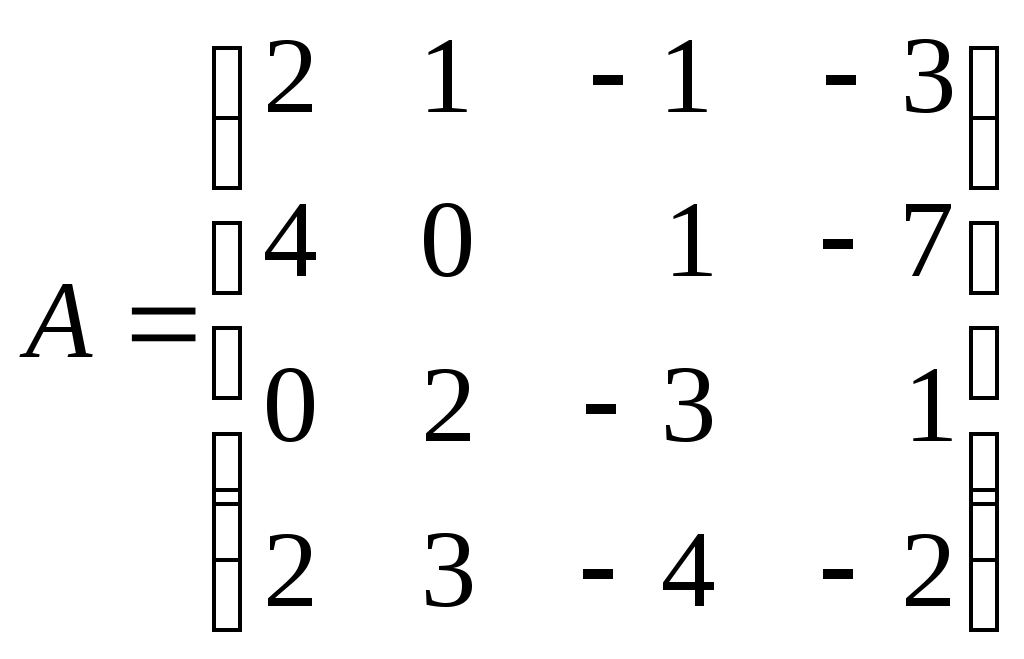 , , 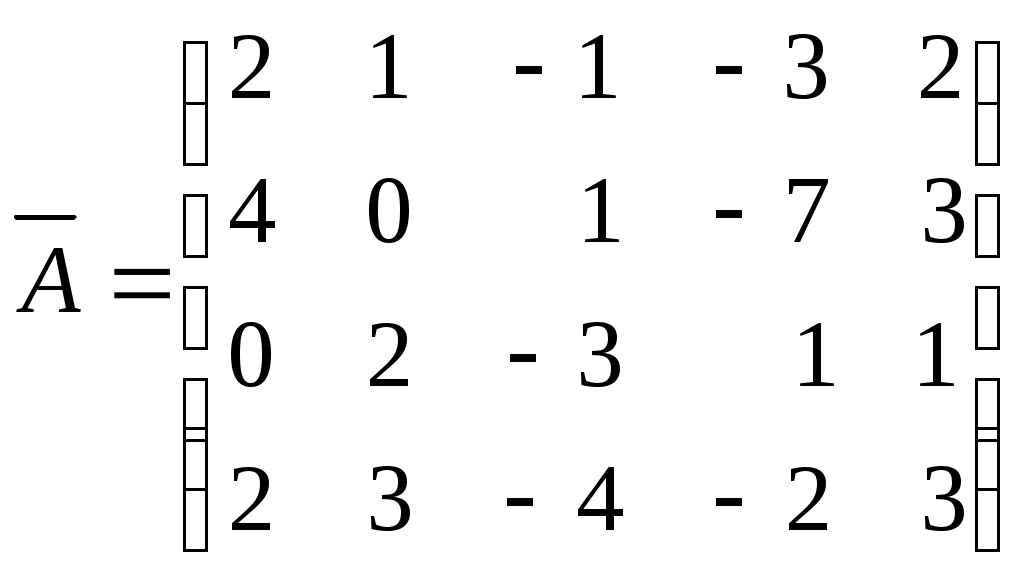 . .Так как Следовательно, оставив 1-е и 2-е уравнения, и, перенеся в правую часть переменные 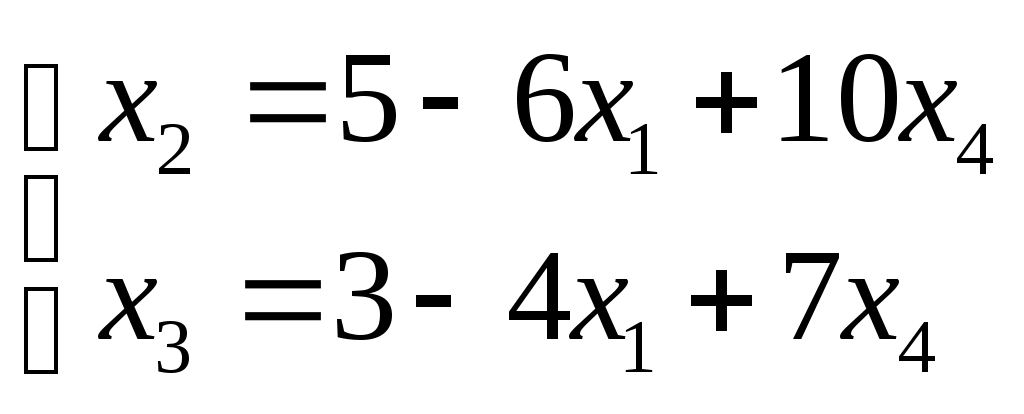 (8) (8) ( 8) – общее решение системы (7), З а м е ч а н и е 1. Систему (7) можно решать непосредственно методом Гаусса. По ходу решения выяснится совместна ли система (7) или нет, и, если совместна, то найдется общее решение. Умножим 1-е уравнение на –2 и сложим его 2-м уравнением. Затем умножим 1-е уравнение на –1 и сложим его 4-м уравнением. Получим 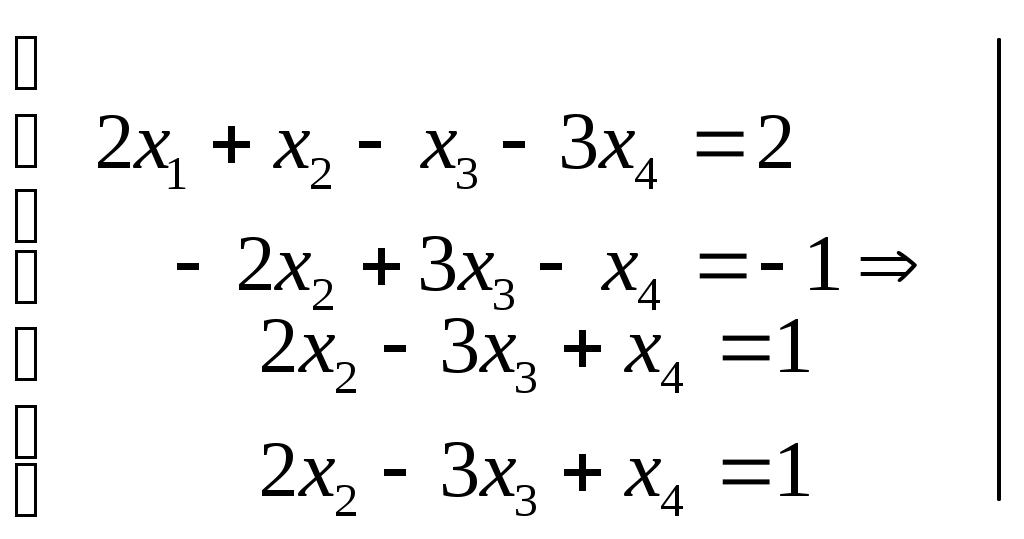 сложим 2-е уравнение с 3-м и 4-м сложим 2-е уравнение с 3-м и 4-м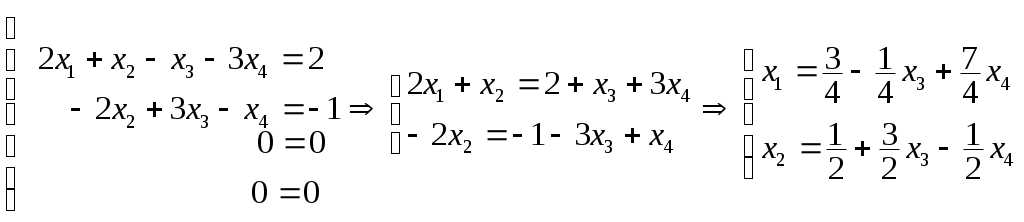 т.е. получили общее решение системы (7), Однородные системы линейных уравнений Рассмотрим систему уравнений Очевидно, что система (10) всегда совместна, так как имеет тривиальное решение Пример 3. 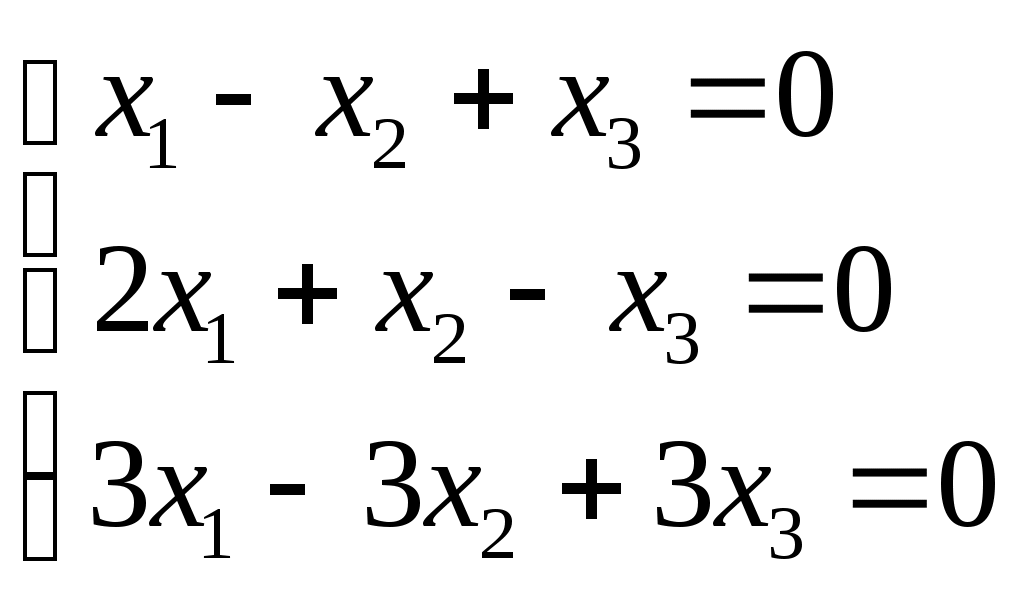 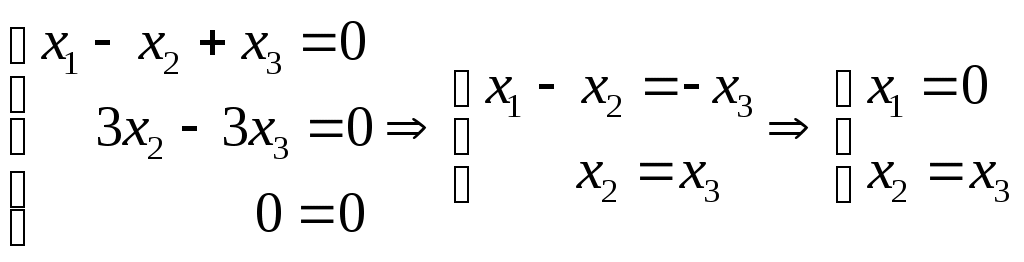 . . |
