|
|
Системи лінійних рівнянь, визначники
Розділ I
ЛІНІЙНА АЛГЕБРА
Тема 1.1 Системи лінійних рівнянь, визначники
1.1.1. Основні поняття
Предметом розгляду лінійної алгебри для економістів є насамперед теорія систем лінійних рівнянь, які в загальному вигляді можна подати так:
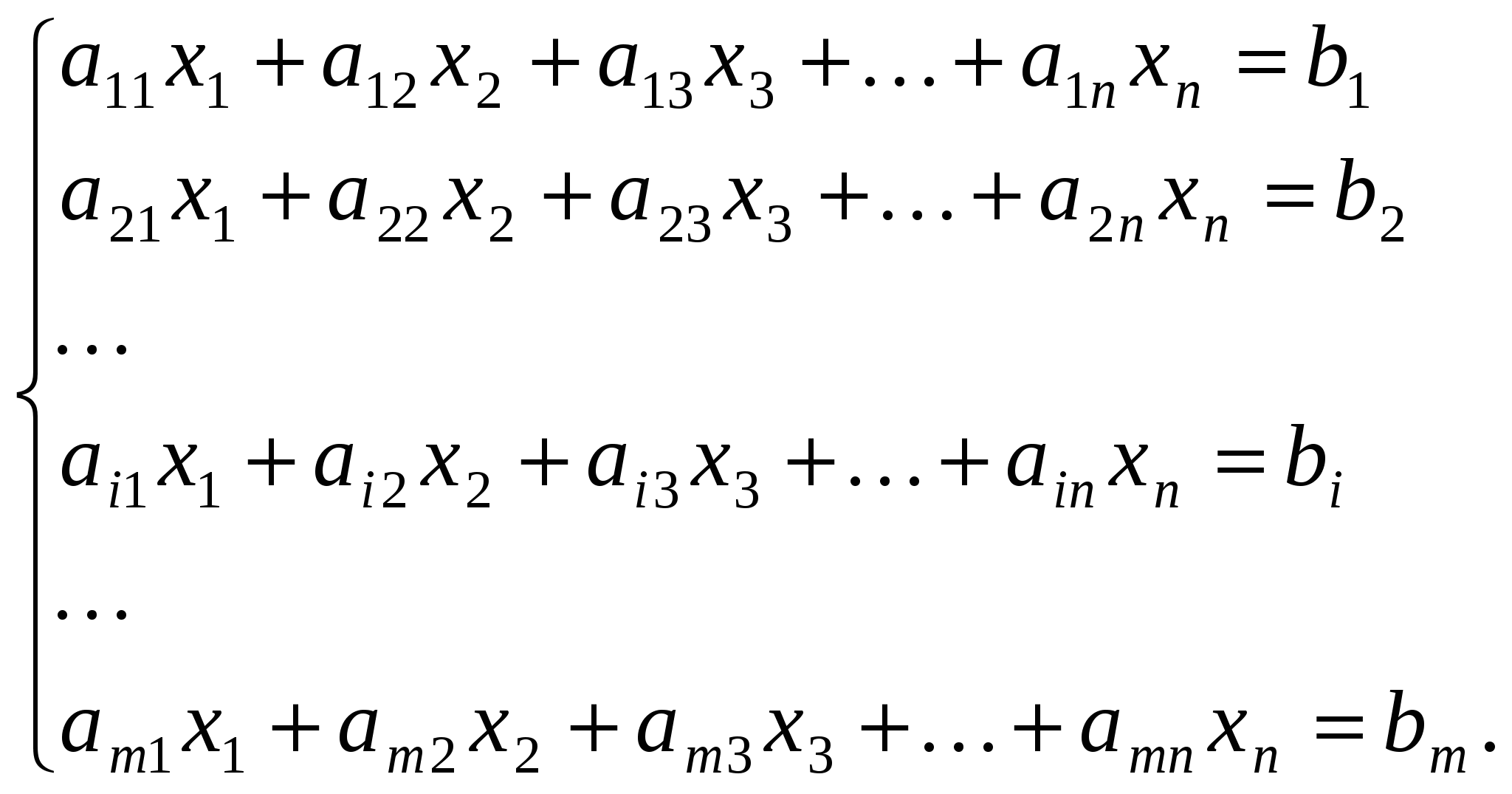 (1.1) (1.1)
Система (1.1) називається системою m лінійних рівнянь з
n невідомими (змінними), де x1, x2, ..., xn— невідомі; aij 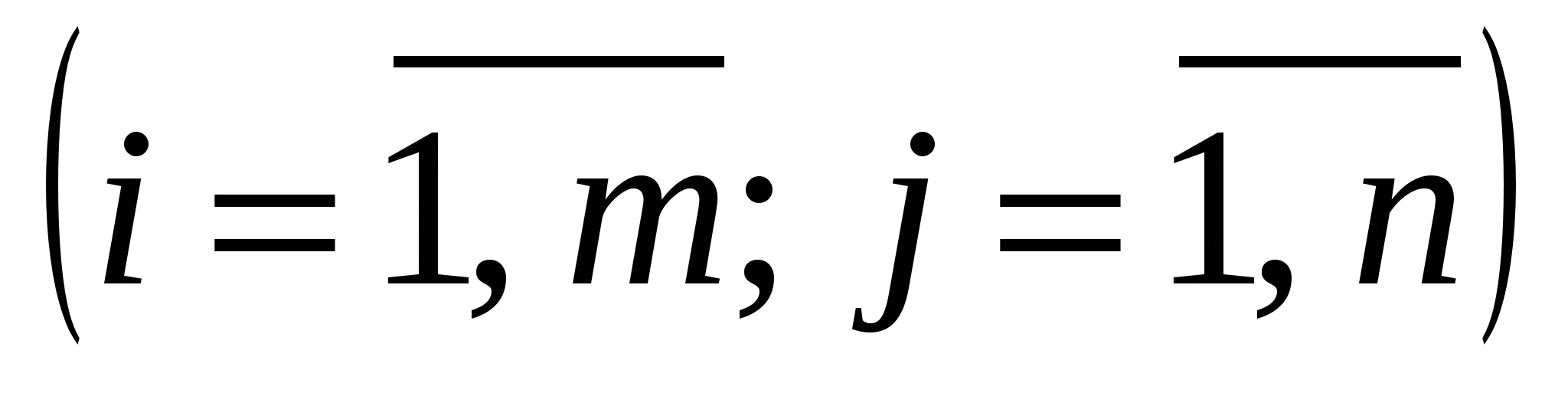 — коефіцієнти системи рівнянь; bi — коефіцієнти системи рівнянь; bi 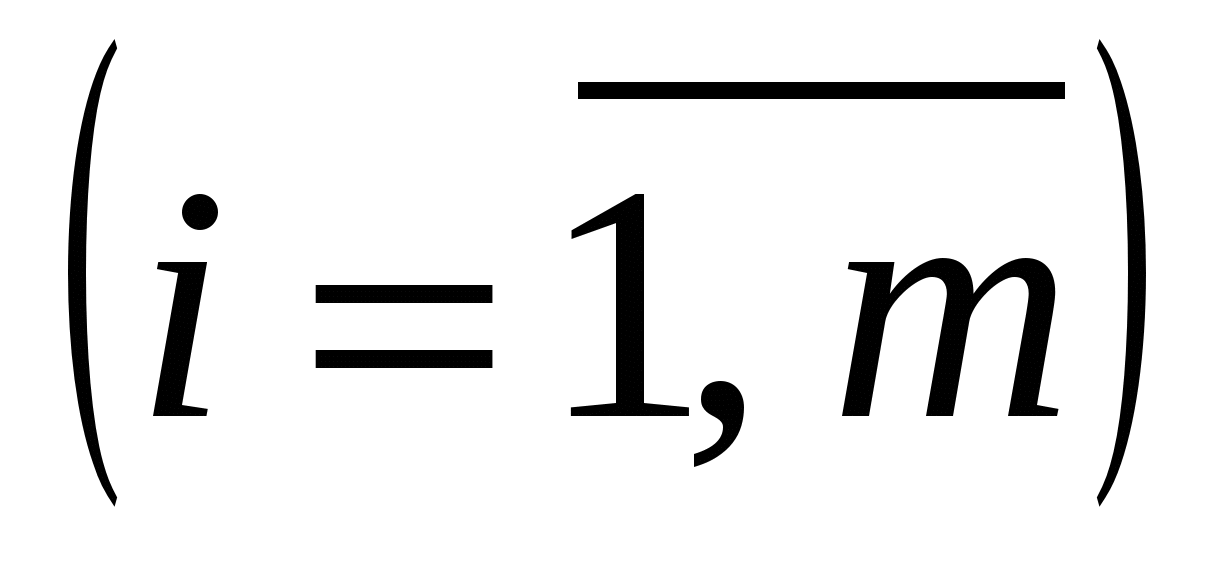 — вільні члени, або праві частини системи рівнянь. Якщо всі — вільні члени, або праві частини системи рівнянь. Якщо всі
bi= 0 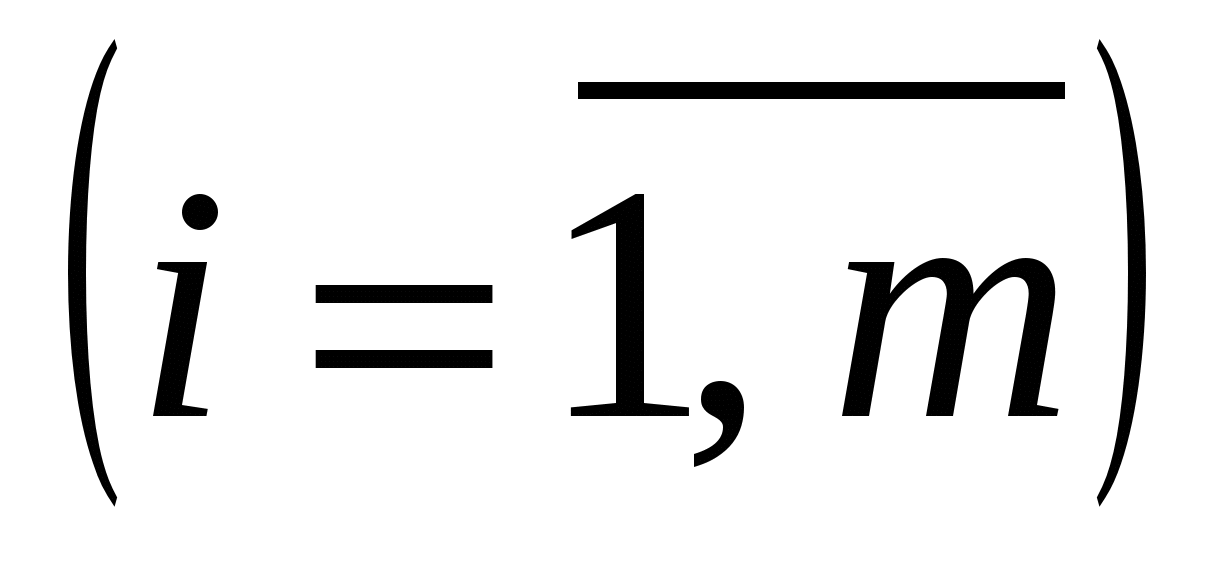 , то система лінійних рівнянь називається однорідною. , то система лінійних рівнянь називається однорідною.
Розв’язком системи рівнянь (1.1) є множина таких чисел
k1, k2, ..., kn, у результаті підставляння яких замість від-
повідних невідомих x1, x2, ..., xn у кожне з рівнянь систе-
ми (1.1) останні перетворюються на правильні числові рів-
ності.
Якщо система рівнянь не має жодного розв’язку, вона називається несумісною, а якщо має хоча б один розв’язок — сумісною. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо розв’язків більш як один.
1.1.2. Визначники другого і третього порядків,
їх властивості
Розглянемо спочатку системи рівнянь, в яких кількість невідомих і кількість рівнянь рівні між собою, тобто m = n. Нехай, наприклад, n = m = 2, тоді маємо систему двох лінійних рівнянь з двома невідомими:
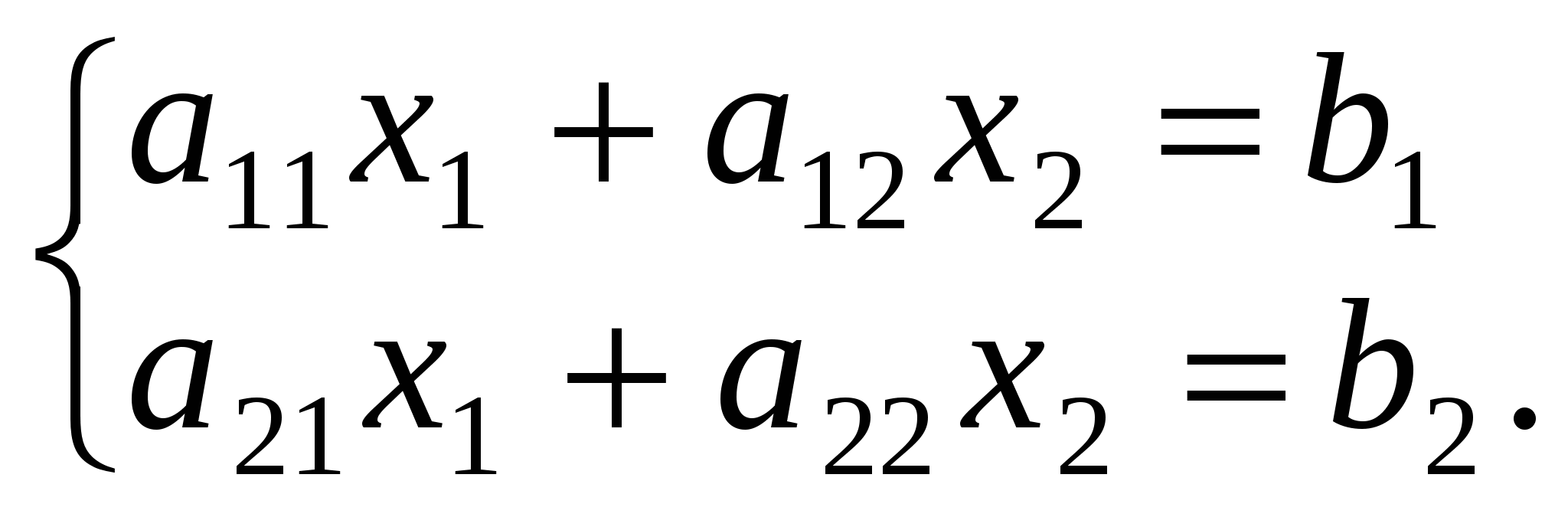
Визначником другого порядку називається вираз
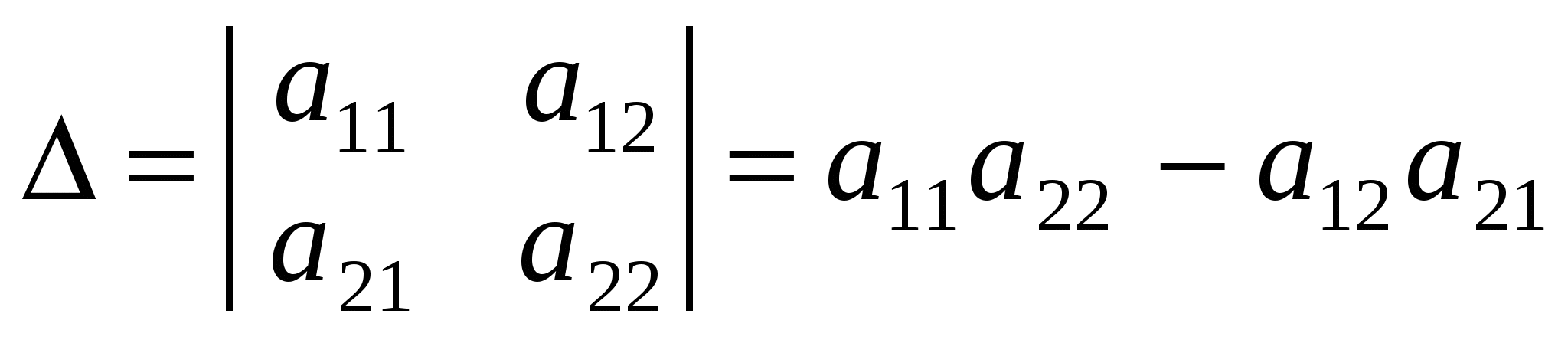 . .
Приклад.
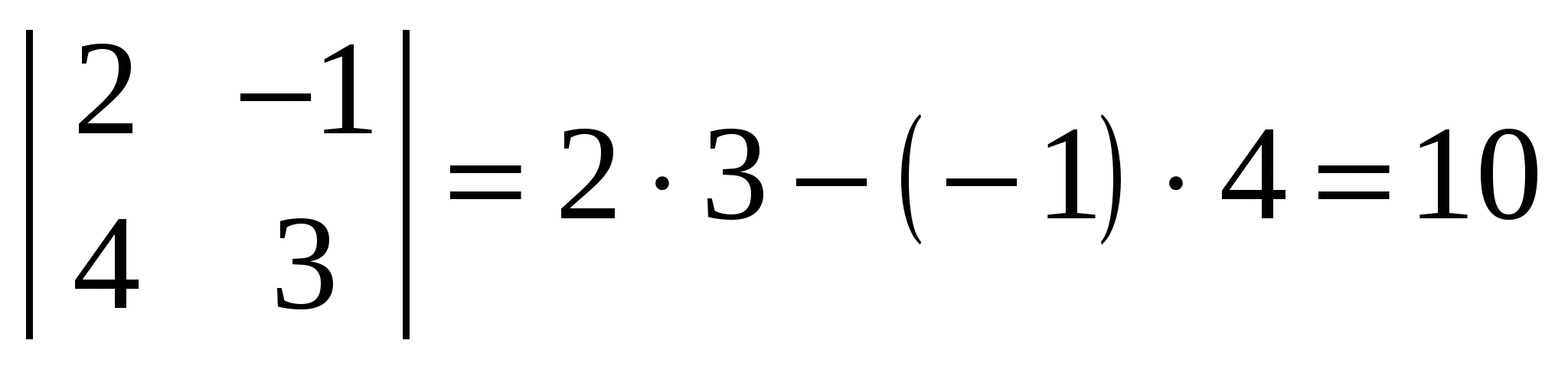 . .
Якщо n= m= 3, то маємо систему трьох лінійних рівнянь з трьома невідомими:
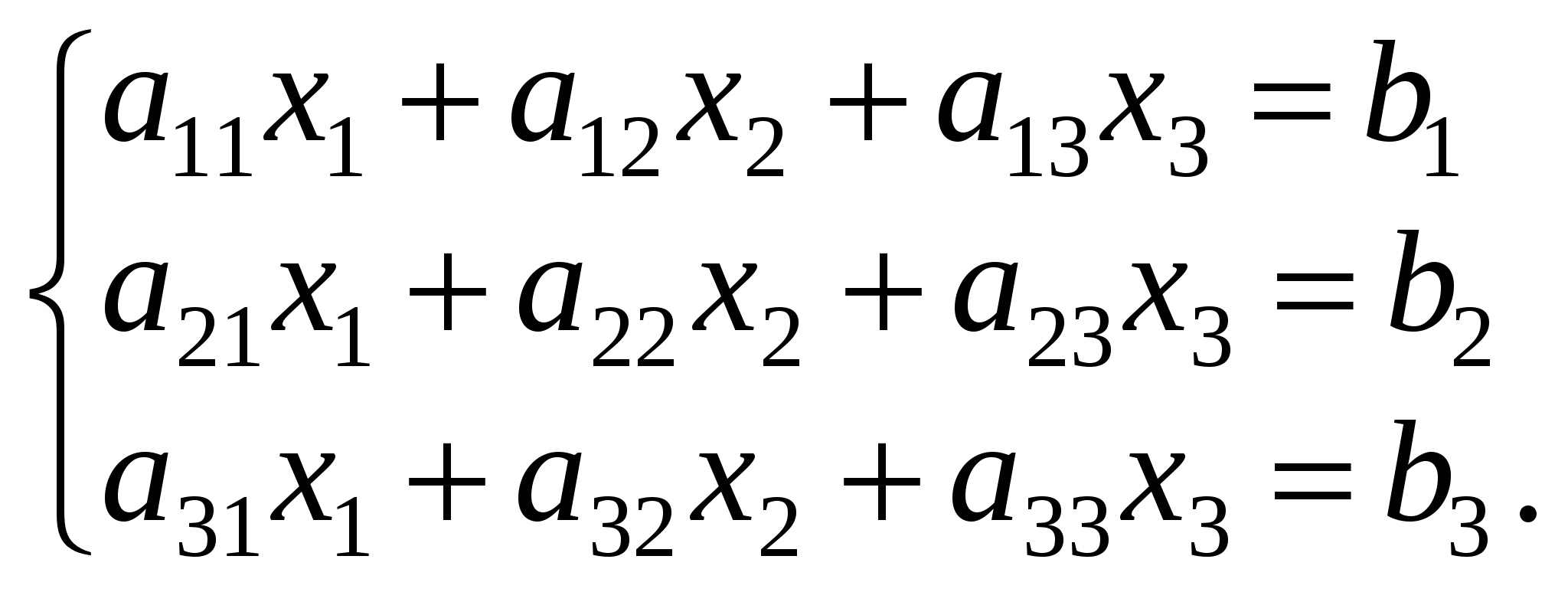
Визначником третього порядку називається вираз:
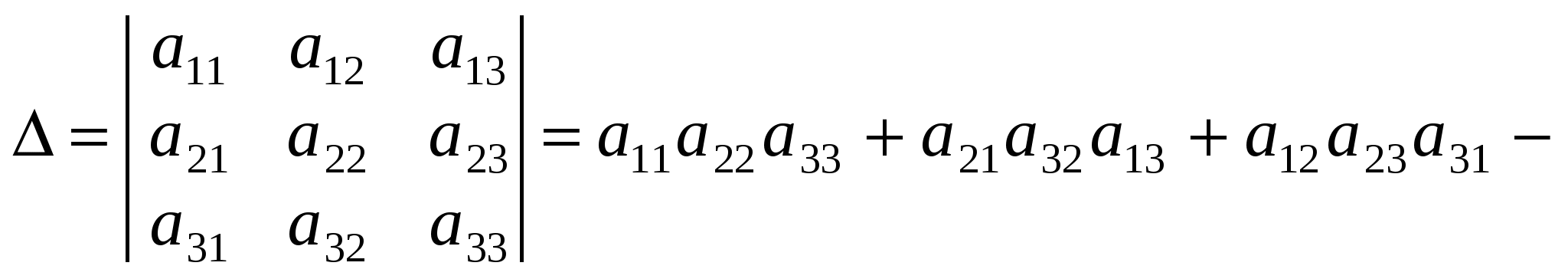
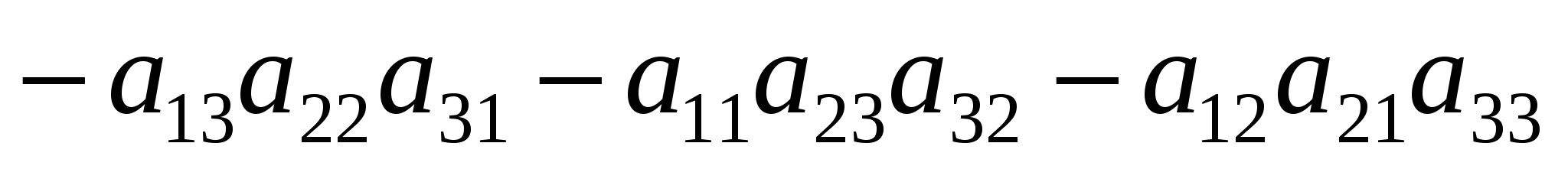 . (1.2) . (1.2)
Для запам’ятовування правила обчислення визначника третього порядку пропонуємо таку схему (правило трикутників):
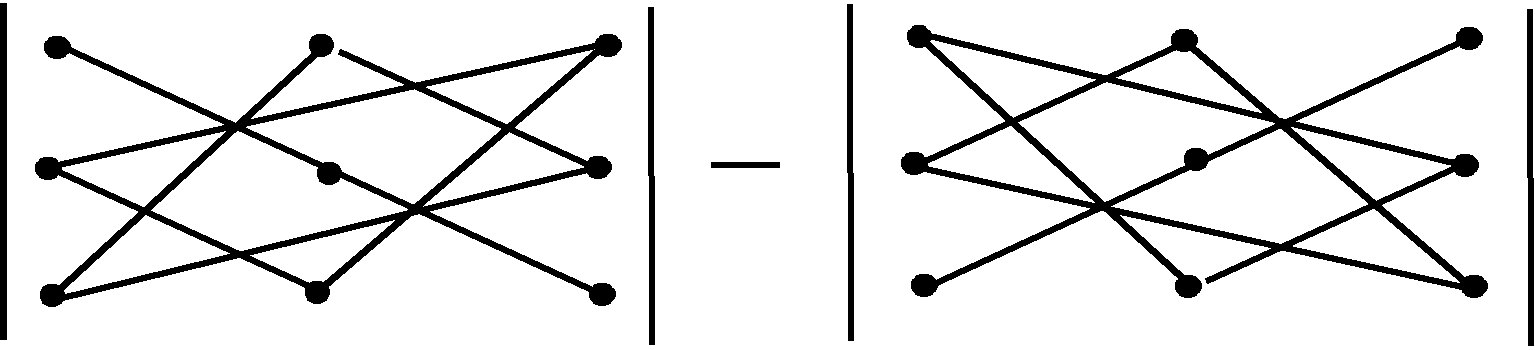
Позначимо точками елементи визначника, тоді доданки зі знаком «плюс» — це добутки елементів a11, a22, a33, розміщених на головній діагоналі визначника, і добутки елементів a13, a21, a32і a12, a23, a31, розміщених у вершинах рівнобедрених трикутників, основи яких паралельні головній діагоналі. Зі знаком «мінус» беруться доданки, що є добутками елементів a13, a22, a31, розміщених на сторонній діагоналі визначника, та у вершинах рівнобедрених трикутників, основи яких паралельні сторонній діагоналі визначника — a11, a23, a32 і a12, a21, a33.
Запропонуємо ще одне правило обчислення визначника третього порядку (правило Саррюса).
У початковому визначнику за третім стовпцем запишемо ще раз перший і другий стовпці:
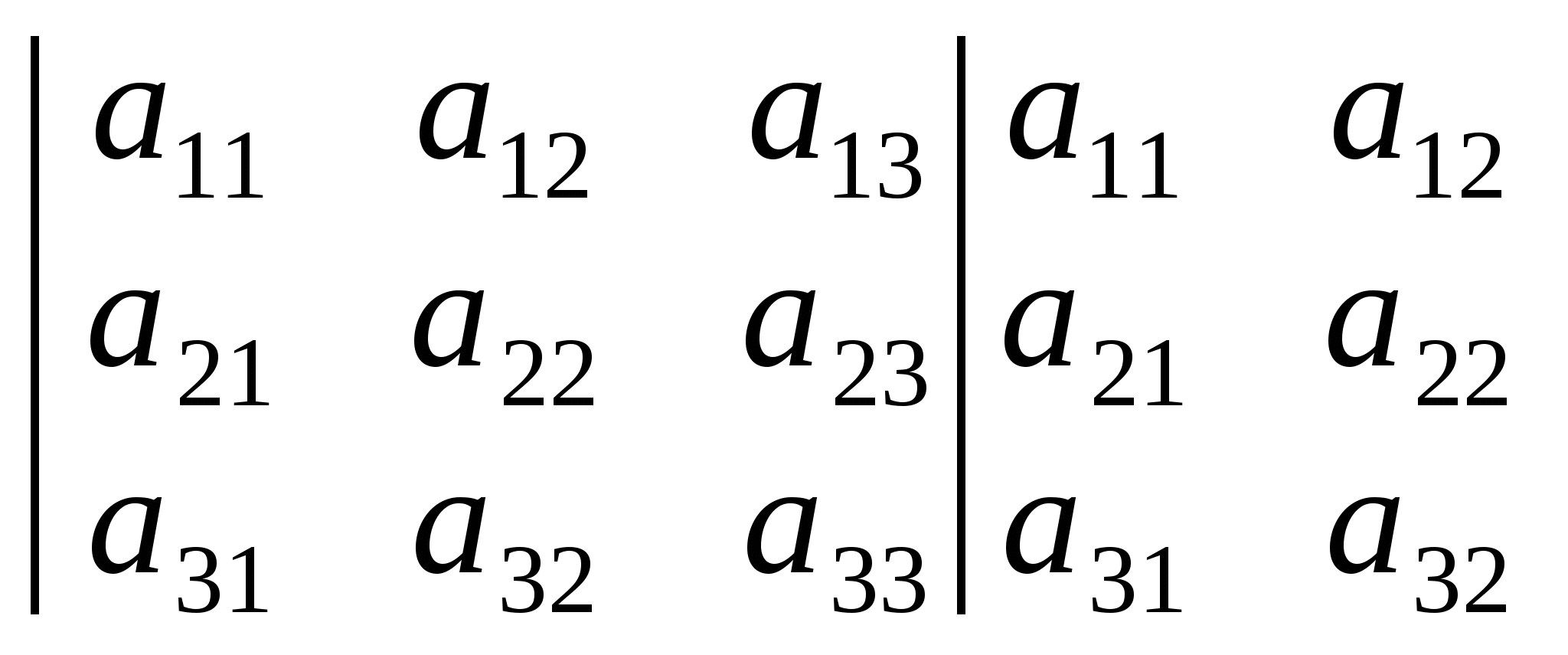
Для знаходження визначника за цим правилом треба утворити зі знаком «плюс» алгебраїчну суму добутків елементів, розміщених на головній діагоналі визначника, і на діагоналях, паралельних їй, а зі знаком «мінус» — добутків елементів, розміщених на сторонній діагоналі, та на діагоналях, пара-
лельних їй.
Визначник:
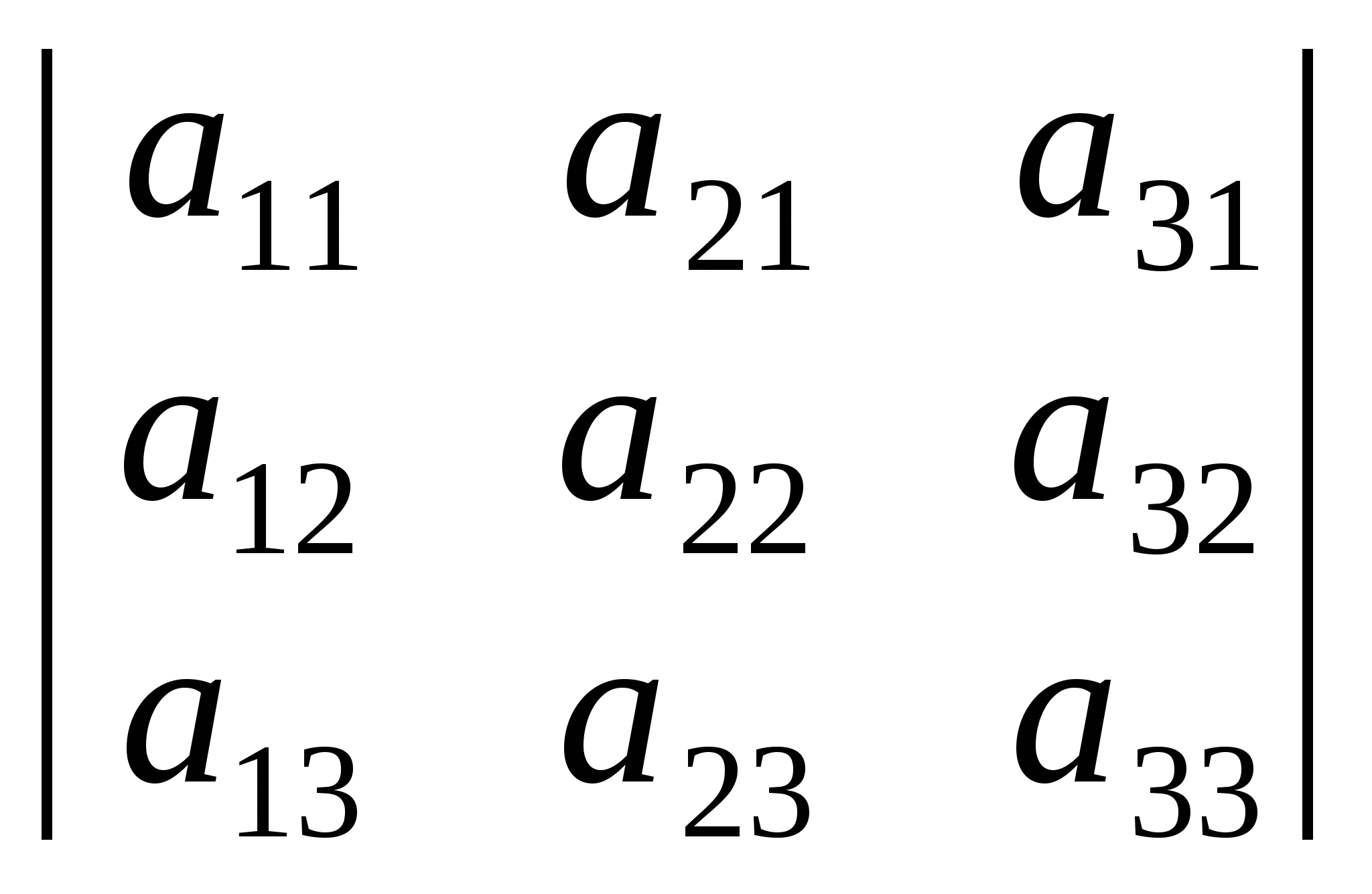 , ,
рядки якого є стовпцями попереднього визначника, є транспонованим щодо визначника (1.2).
Властивість 1. Визначник не змінюється в результаті транспонування.
З властивості 1 випливає, що будь-яке твердження, котре справджується для рядків визначника, справджується і для його стовпців, і навпаки.
Властивість 2. Якщо один із рядків визначника складається лише з нулів, то такий визначник дорівнює нулю.
Властивість 3. Якщо поміняти місцями будь-які два рядки визначника, то його знак зміниться на протилежний.
Властивість 4. Визначник, який має два однакові рядки, дорівнює нулю.
Властивість 5. Якщо елементи будь-якого рядка визначника помножити на стале число С, то й визначник помножиться на С.
З останньої властивості випливає, що спільний множник елементів рядка можна виносити за знак визначника.
Властивість 6. Визначник, який має два пропорційні рядки, дорівнює нулю.
Властивість 7. Якщо всі елементи будь-якого рядка визначника можна подати у вигляді суми двох доданків, то такий визначник дорівнює сумі двох визначників, у яких елементами цього рядка будуть відповідно перший доданок у першому визначнику і другий доданок у другому визначнику, а решта елементів будуть ті самі, що й у початковому визначнику.
Властивість 8. Визначник не зміниться, якщо до елементів будь-якого рядка додати відповідні елементи довільного іншого рядка, попередньо помножені не деяке число.
1.1.3. Мінори та алгебраїчні доповнення
Нехай визначник має n рядків і n стовпців. Мінором k-го порядку k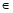 [1; n–1] називається визначник, утворений з елементів, розміщених на перетині будь-яких k рядків і k стовпців визначника. Зрозуміло, що мінор першого порядку — це будь-який елемент визначника. [1; n–1] називається визначник, утворений з елементів, розміщених на перетині будь-яких k рядків і k стовпців визначника. Зрозуміло, що мінор першого порядку — це будь-який елемент визначника.
Приклад. Утворити кілька мінорів другого і один мінор третього порядку такого визначника:
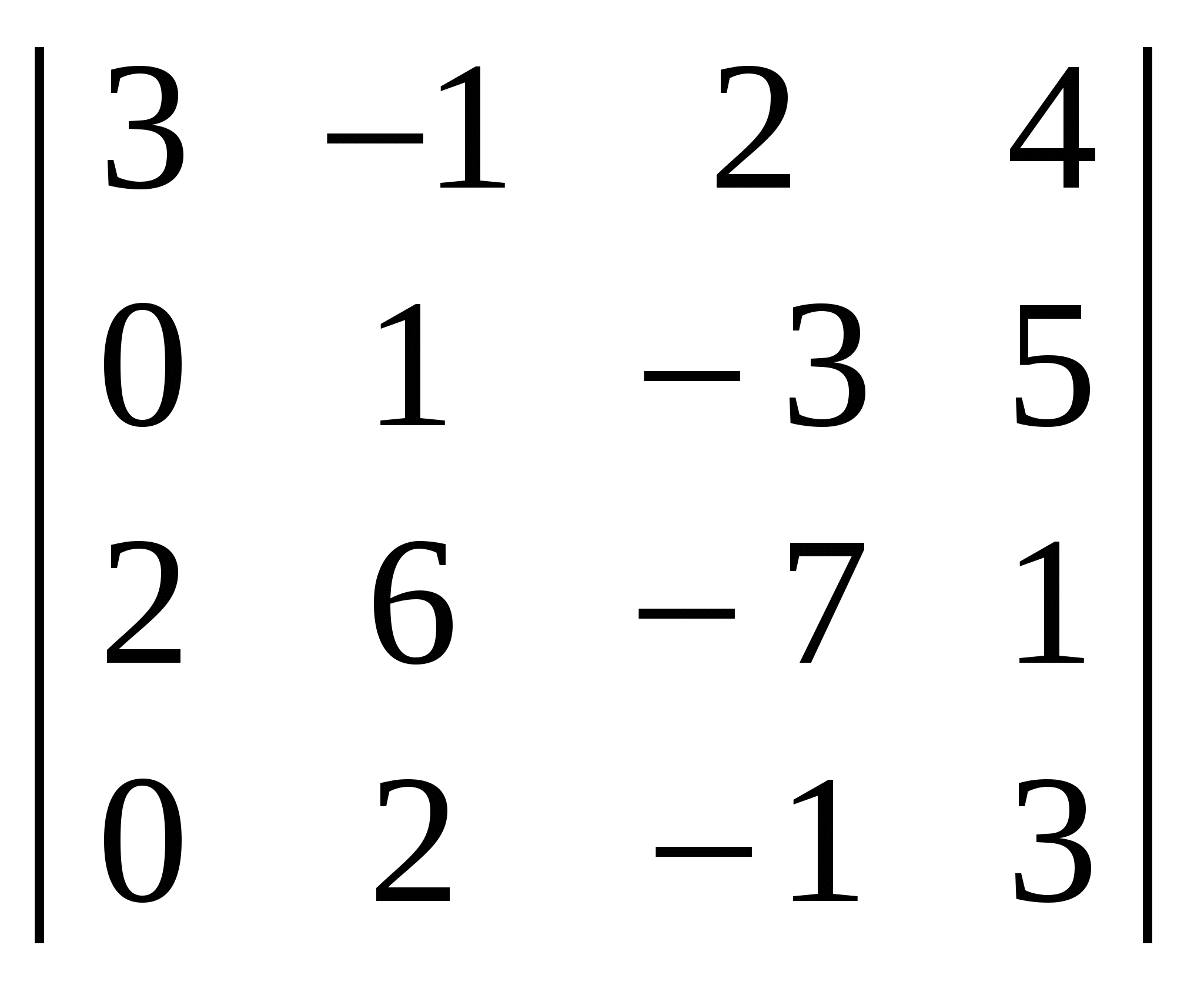 . .
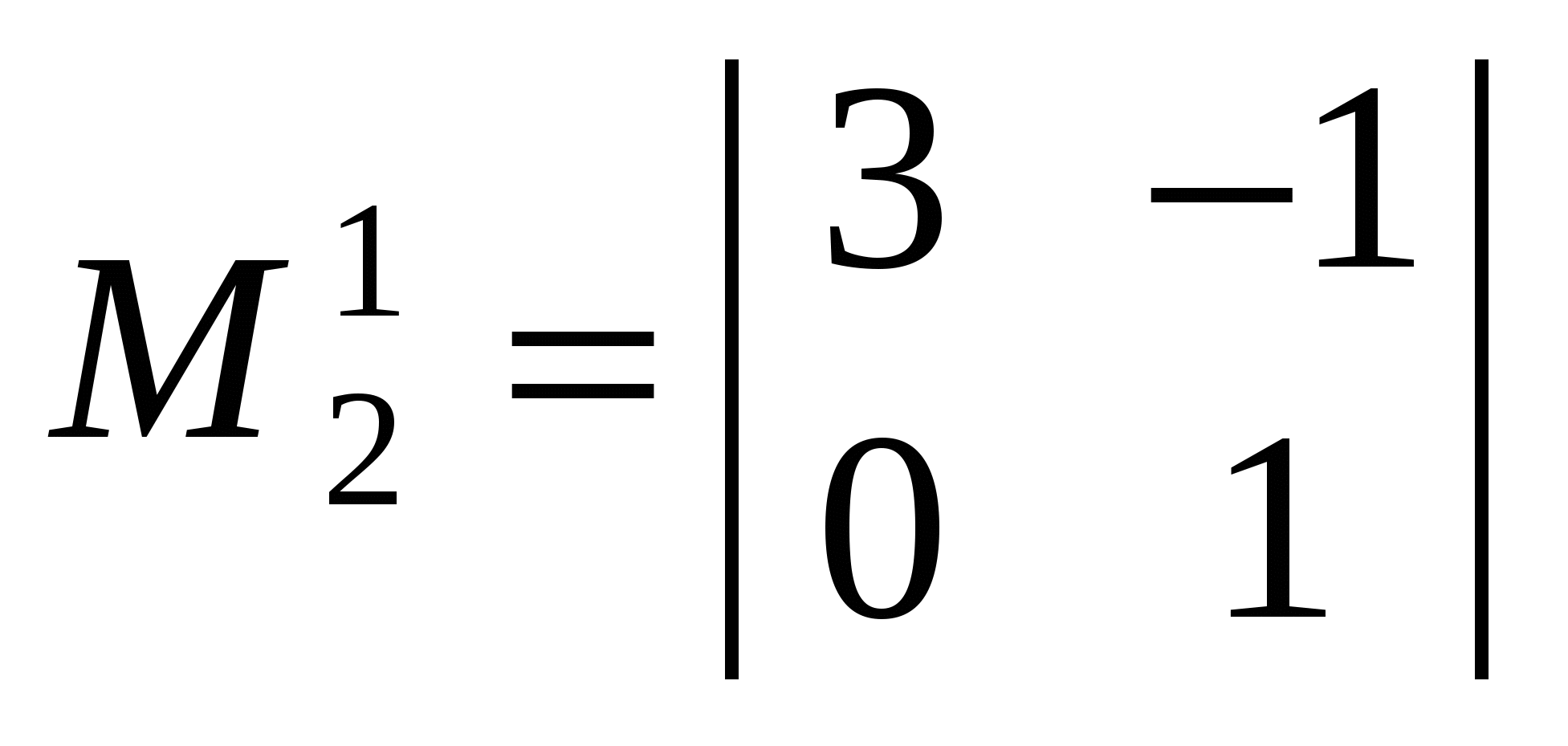 , , 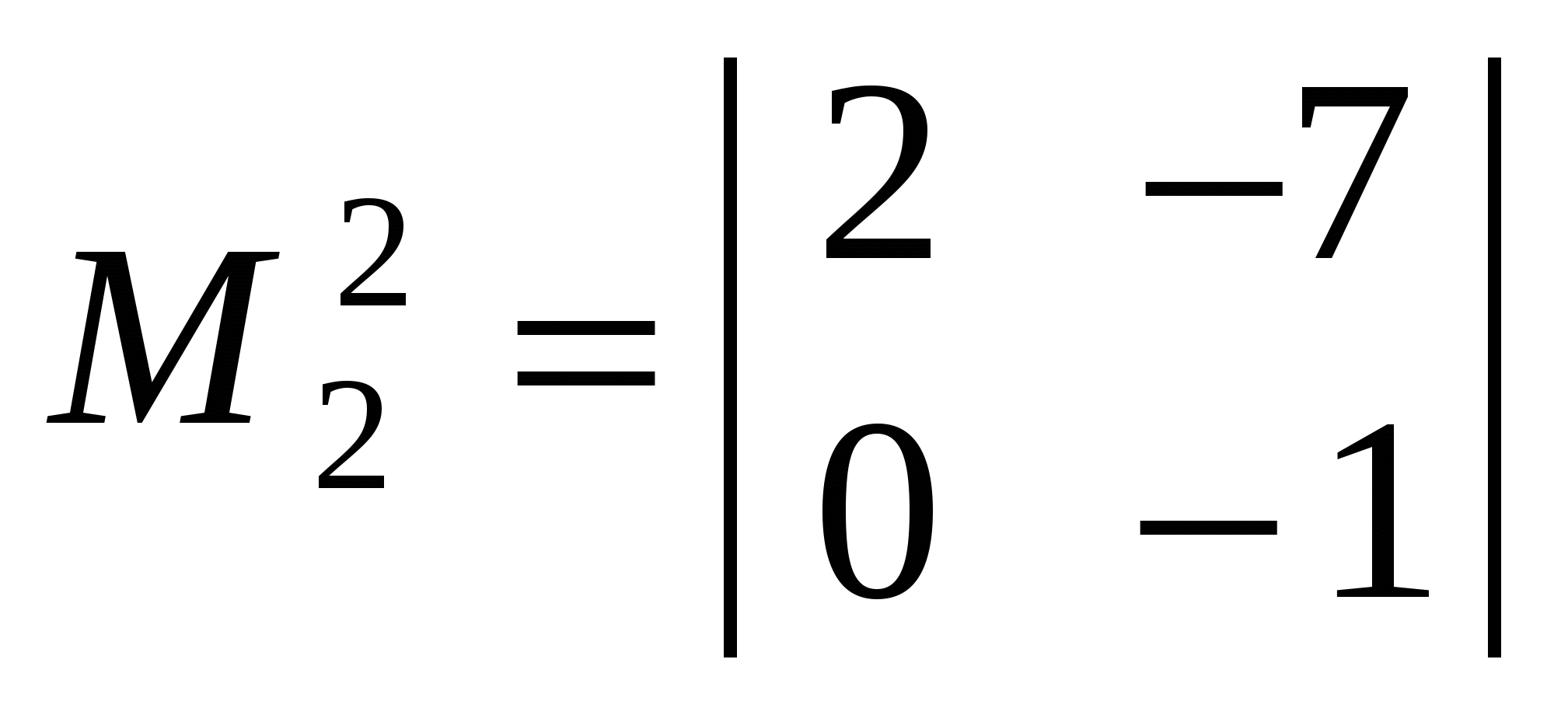 , , 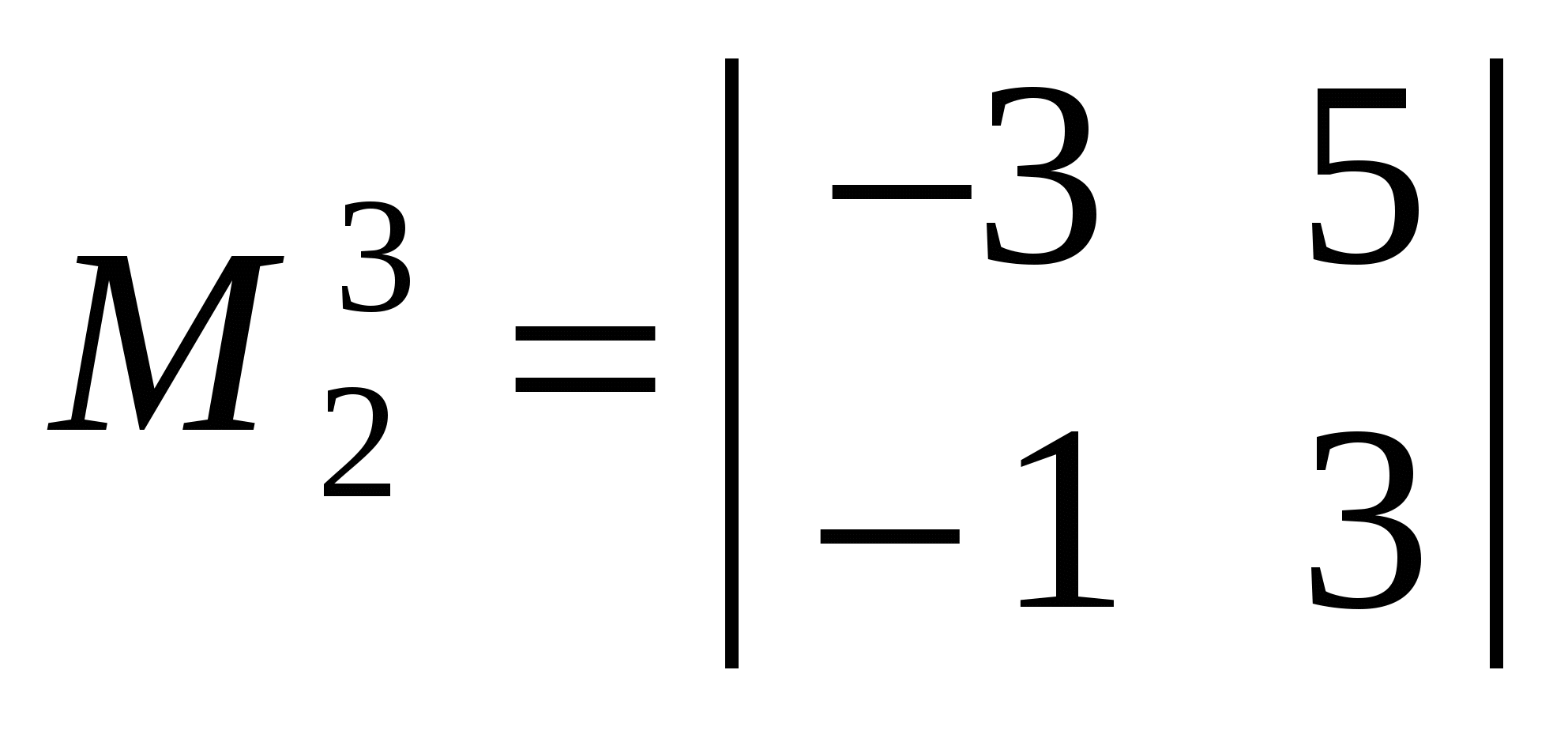 , ... , , ... , 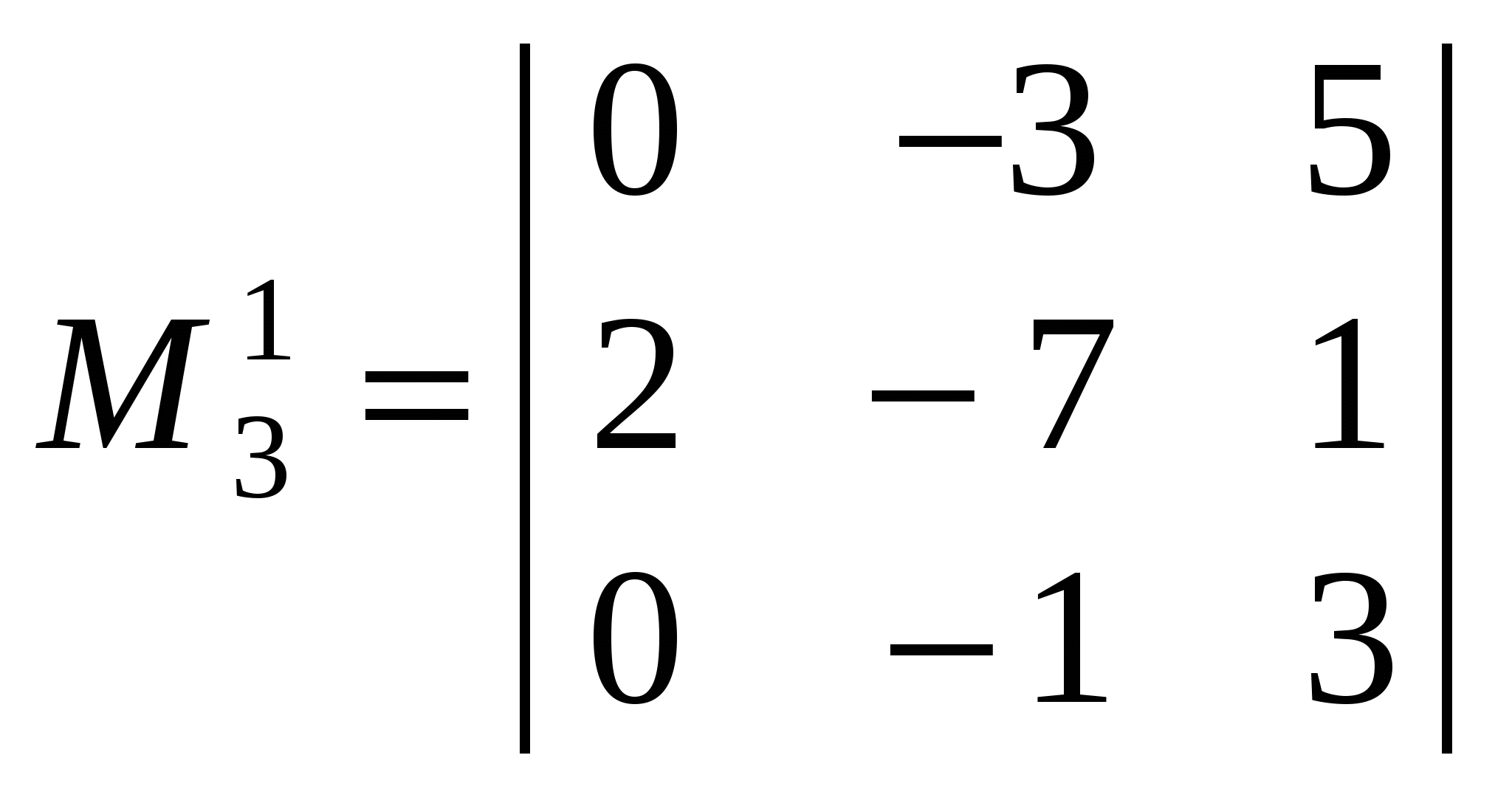 . .
Мінори 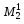 , , 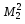 , , 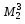 другого порядку утворюються з елементів, розміщених на перетині першого, другого рядків; першого, другого стовпців; третього, четвертого рядків; першого, третього стовпців; другого, четвертого рядків; третього, четвертого стовпців. Мінор другого порядку утворюються з елементів, розміщених на перетині першого, другого рядків; першого, другого стовпців; третього, четвертого рядків; першого, третього стовпців; другого, четвертого рядків; третього, четвертого стовпців. Мінор 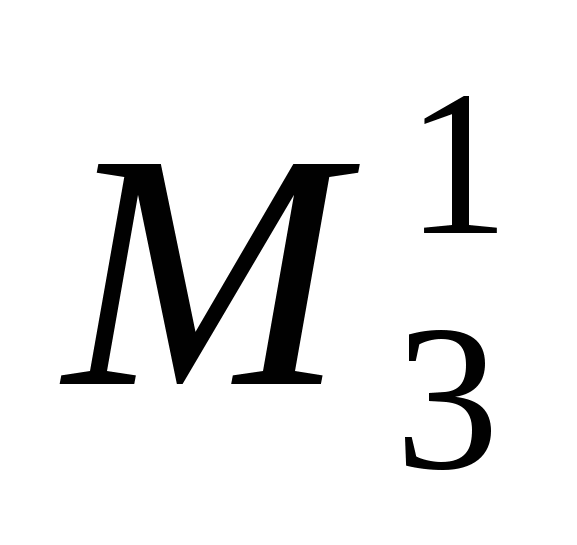 третього порядку утворюється з елементів, розміщених на перетині другого, третього, четвертого рядків і першого, третього, четвертого стовпців. третього порядку утворюється з елементів, розміщених на перетині другого, третього, четвертого рядків і першого, третього, четвертого стовпців.
Верхній індекс означає нумерацію мінорів; нижній індекс — порядок мінора.
Доповняльним мінором для мінора k-го порядку називається такий мінор, який лишається у визначнику після викреслювання тих k рядків і тих k стовпців, на перетині яких містяться елементи, що утворили мінор k-го порядку.
Нехай мінор k-го порядку утворено з елементів, розміщених на перетині i1, i2, ..., ik рядків і j1, j2, ..., jk стовпців.
Алгебраїчним доповненням до мінора k-го порядку є допов-
няльний мінор (n–k)-го порядку, узятий зі знаком 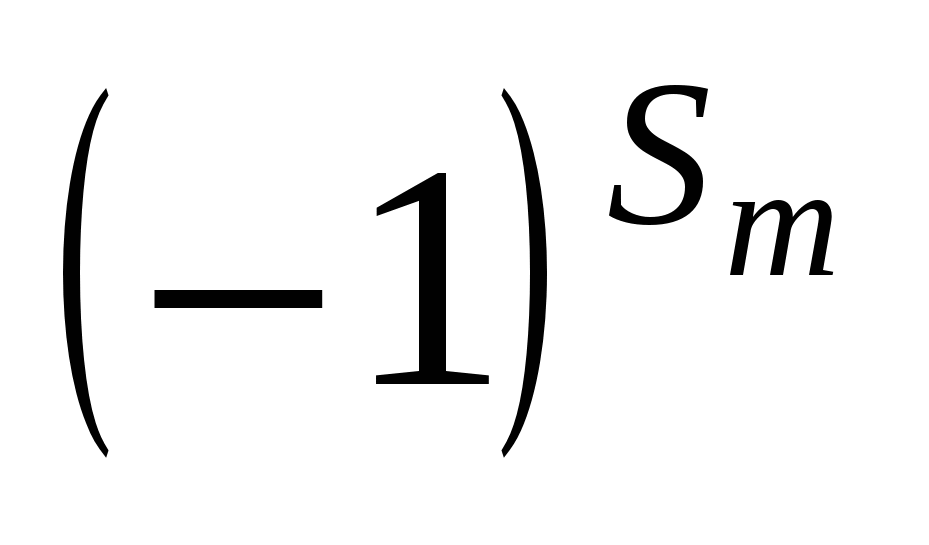 , де , де 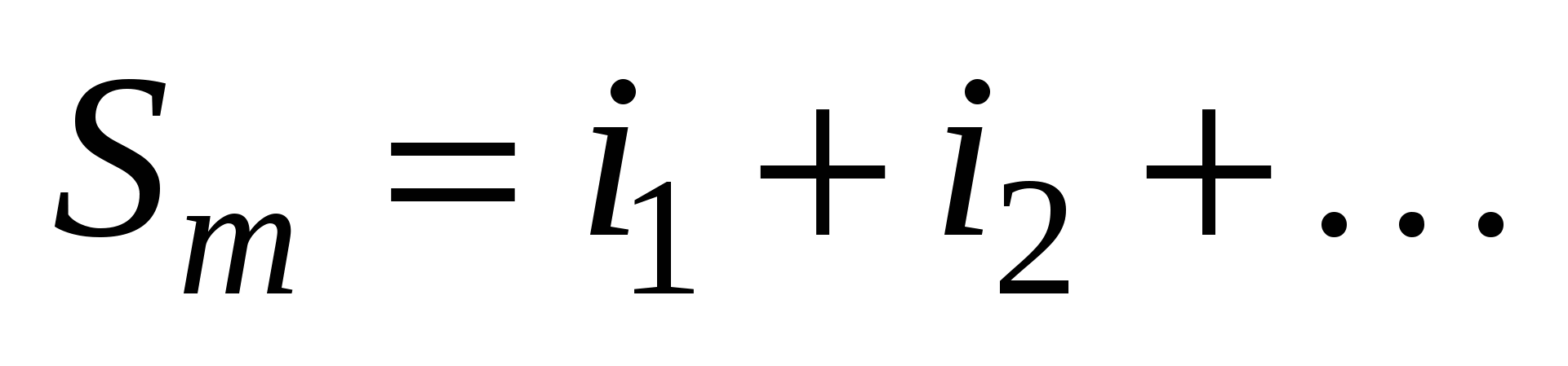 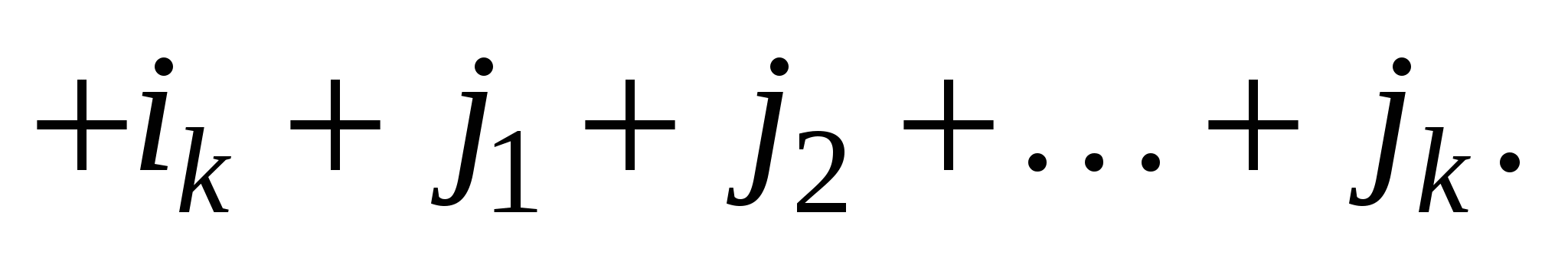 Якщо сума Якщо сума 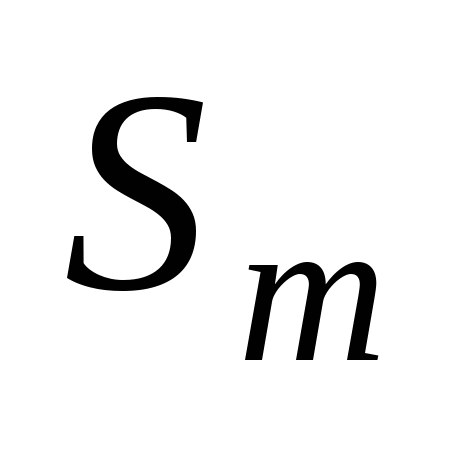 номерів рядків і стовпців парна, то береться знак «+», якщо непарна — то знак «–». номерів рядків і стовпців парна, то береться знак «+», якщо непарна — то знак «–».
Далі важливу роль відіграватиме алгебраїчне доповнення до мінора першого порядку. Нехай 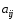 — будь-який елемент-мінор першого порядку у визначнику n-го порядку, тоді — будь-який елемент-мінор першого порядку у визначнику n-го порядку, тоді 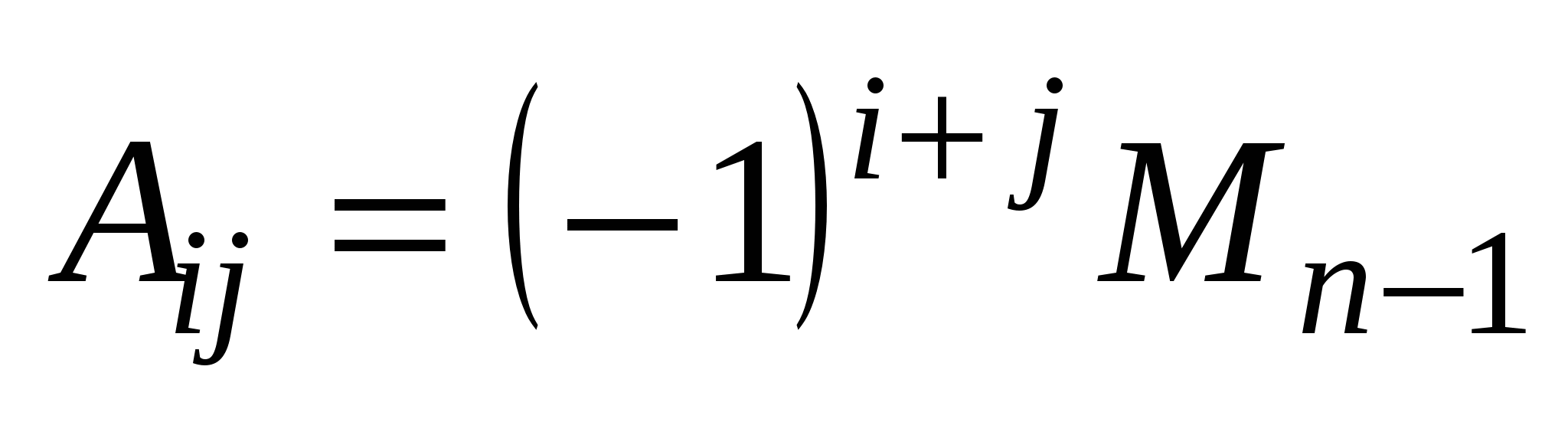 буде алгебраїчним доповненням до мінора буде алгебраїчним доповненням до мінора  . Тут . Тут 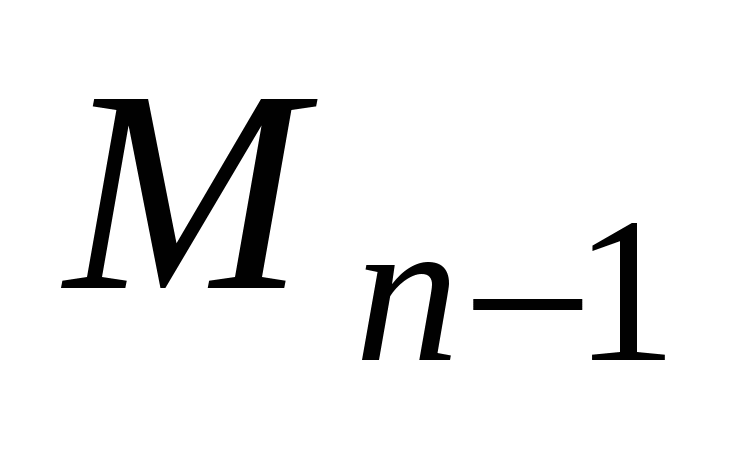 — доповняльний мінор (n–1)-го порядку, утворений викреслюванням — доповняльний мінор (n–1)-го порядку, утворений викреслюванням
i-рядка і j-стовпця в початковому визначнику n-го порядку.
1.1.4. Обчислення визначників
Означення. Визначником n-го порядку називається число  , яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпця на відповідні їм алгебраїчні доповнення: , яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпця на відповідні їм алгебраїчні доповнення:
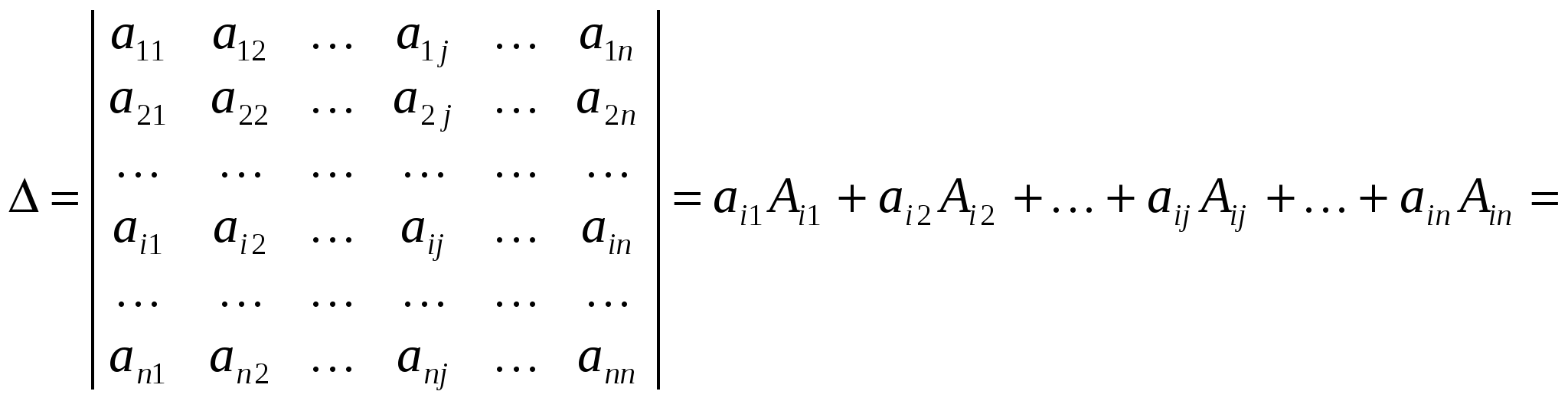
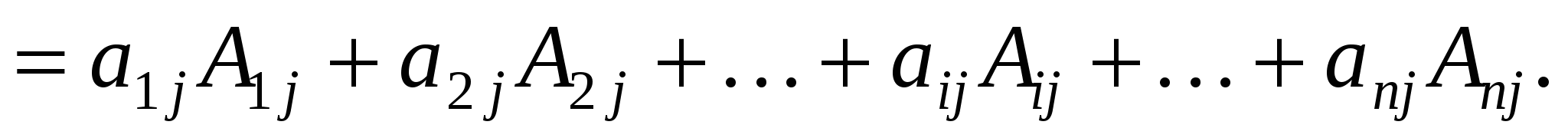 (1.3) (1.3)
Алгебраїчні доповнення, що входять до формули (1.3), за якою обчислюють визначник, є, у свою чергу, мінорами, узятими з відповідними знаками, тобто визначниками (n–1)-го порядку. Отже, обчислення визначника n-го порядку зводиться до обчислення n визначників (n–1)-го порядку.
Але з формули (1.3) випливає, що за наявності у визначнику нульових елементів відповідні алгебраїчні доповнення обчислювати не потрібно.
Згідно з властивістю 8, яка справджується для визначників будь-якого порядку, можна визначник перетворити так, щоб у його рядках або стовпцях усі елементи, крім одного, дорівнювали нулю. І тоді, розклавши визначник за елементами цього рядка або стовпця, зведемо задачу знаходження визначника n-го порядку до знаходження одного визначника n–1-го порядку.
Властивість 9. Сума добутків елементів рядка або стовпця визначника n-го порядку на алгебраїчні доповнення до елементів іншого рядка або стовпця цього самого визначника дорівнює нулю.
1.1.5. Правило Крамера
Розглянемо систему n лінійних рівнянь з n невідомими:
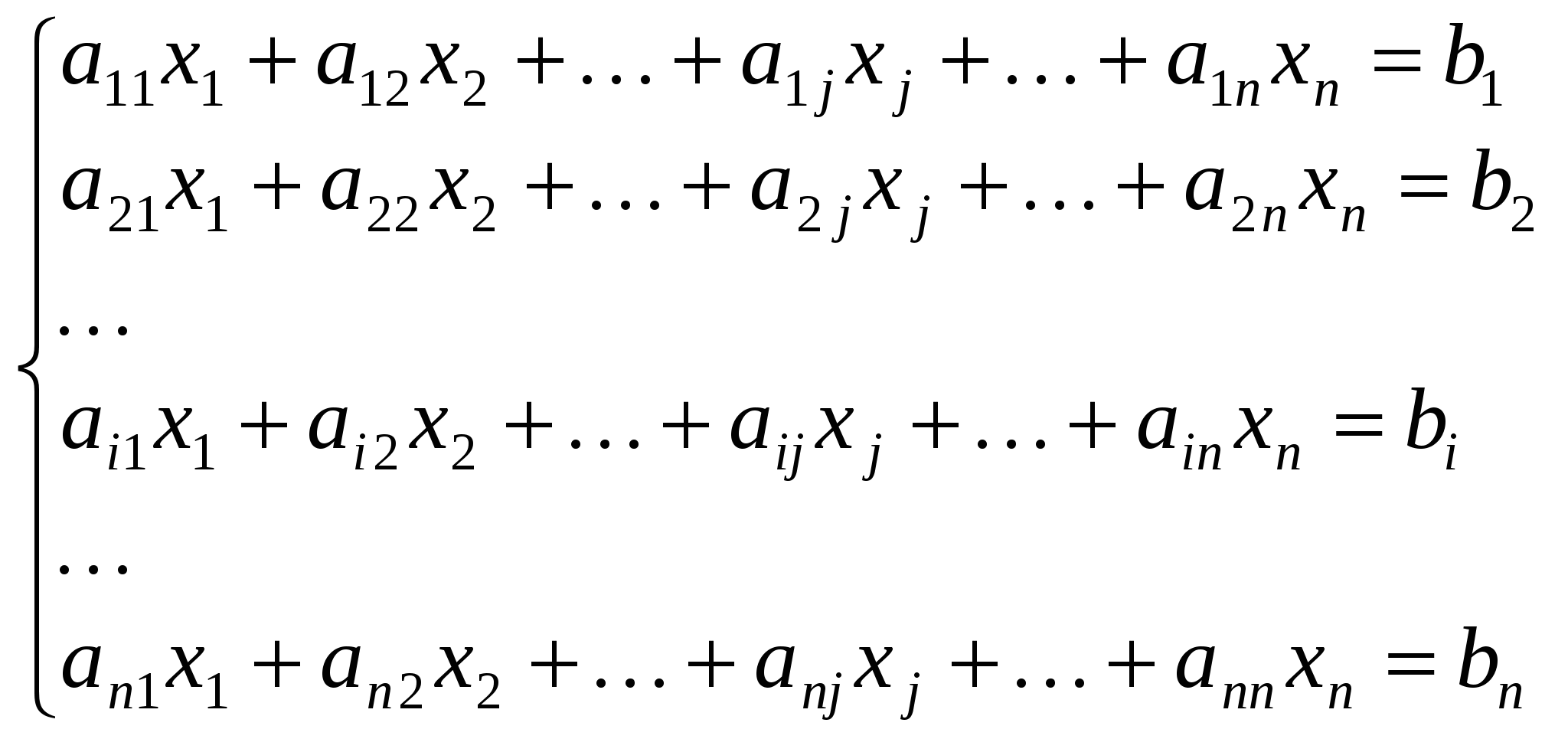 (1.4) (1.4)
Теорема. Якщо головний визначник  складений із коефіцієнтів при невідомих системи n лінійних рівнянь з n невідомими (1.4), відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який обчислюється за формулами: складений із коефіцієнтів при невідомих системи n лінійних рівнянь з n невідомими (1.4), відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який обчислюється за формулами:
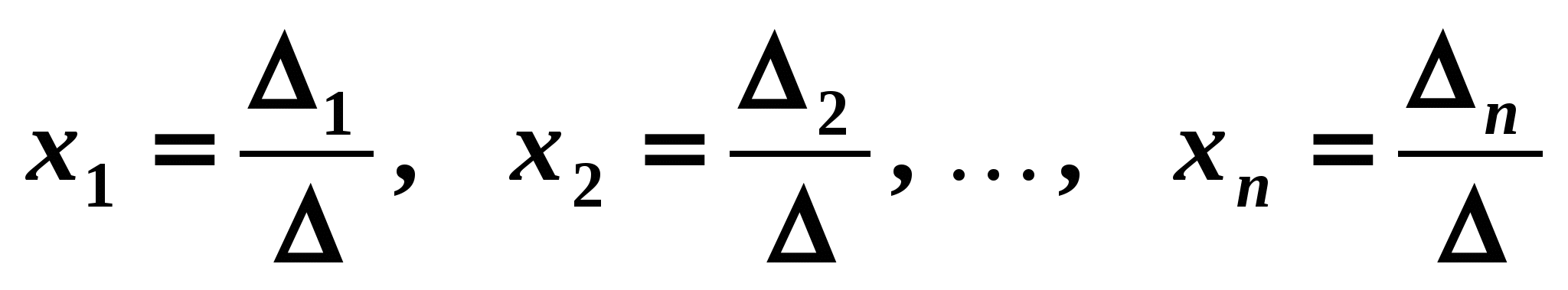 , ,
де  — головний визначник системи, який утворюється з коефіцієнтів при невідомих у лівій частині системи (1.4); — головний визначник системи, який утворюється з коефіцієнтів при невідомих у лівій частині системи (1.4);
 — визначник, який утворюється заміною j-го стовпця в головному визначнику на стовпець вільних членів. — визначник, який утворюється заміною j-го стовпця в головному визначнику на стовпець вільних членів.
План практичних занять
Обчислення визначників третього порядку.
Обчислення визначників n-го порядку.
Розв’язування систем n рівнянь з n невідомими за правилом Крамера.
Термінологічний словник ключових понять
Транспонування — зміна місцями рядків і стовпців визначника або матриці.
Мінор k-го порядку — визначник, утворений з елементів визначника або матриці, розміщених на перетині k рядків і k стовпців.
Алгебраїчне доповнення до мінора — визначник, що складається з елементів, котрі не належать тим рядкам і тим стовпцям визначника, з яких утворено мінор, і береться зі знаком 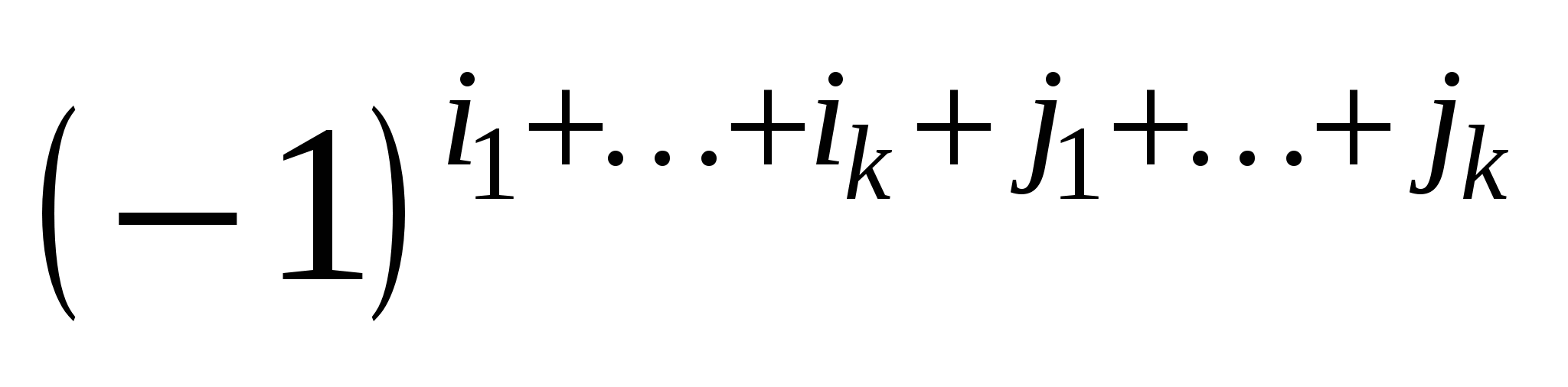 , де i1 i2, ..., ik, j1, j2, ..., jk, — індекси відповідно тих рядків і тих стовпців, які брали участь в утворенні мінора. , де i1 i2, ..., ik, j1, j2, ..., jk, — індекси відповідно тих рядків і тих стовпців, які брали участь в утворенні мінора.
Навчальні завдання
Обчислити визначник за правилом трикутників.
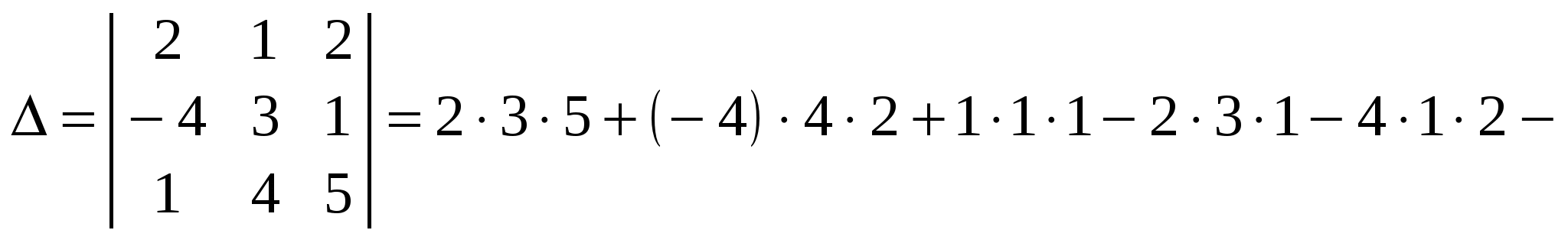
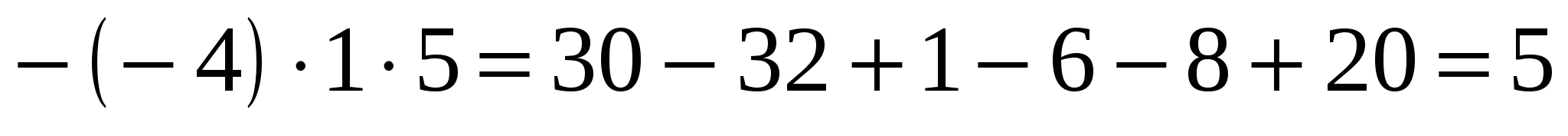 . .
Обчислити визначник за правилом Саррюса.
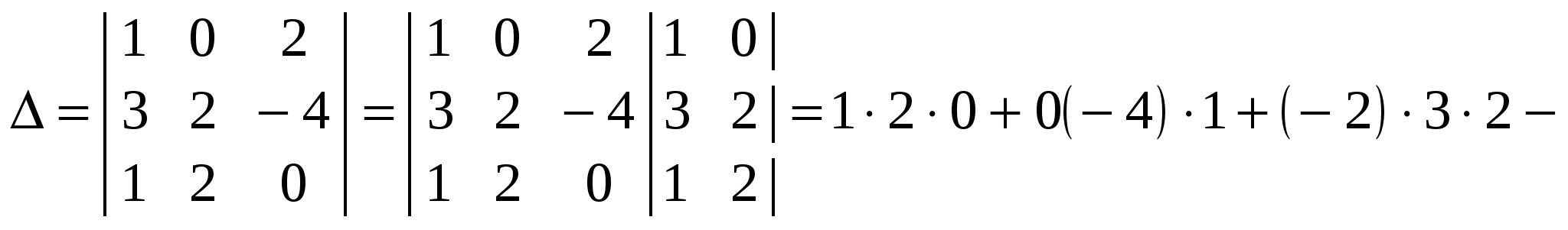
 . .
Утворити доповняльний мінор другого порядку.
Для визначника ∆ запишемо мінор другого порядку:
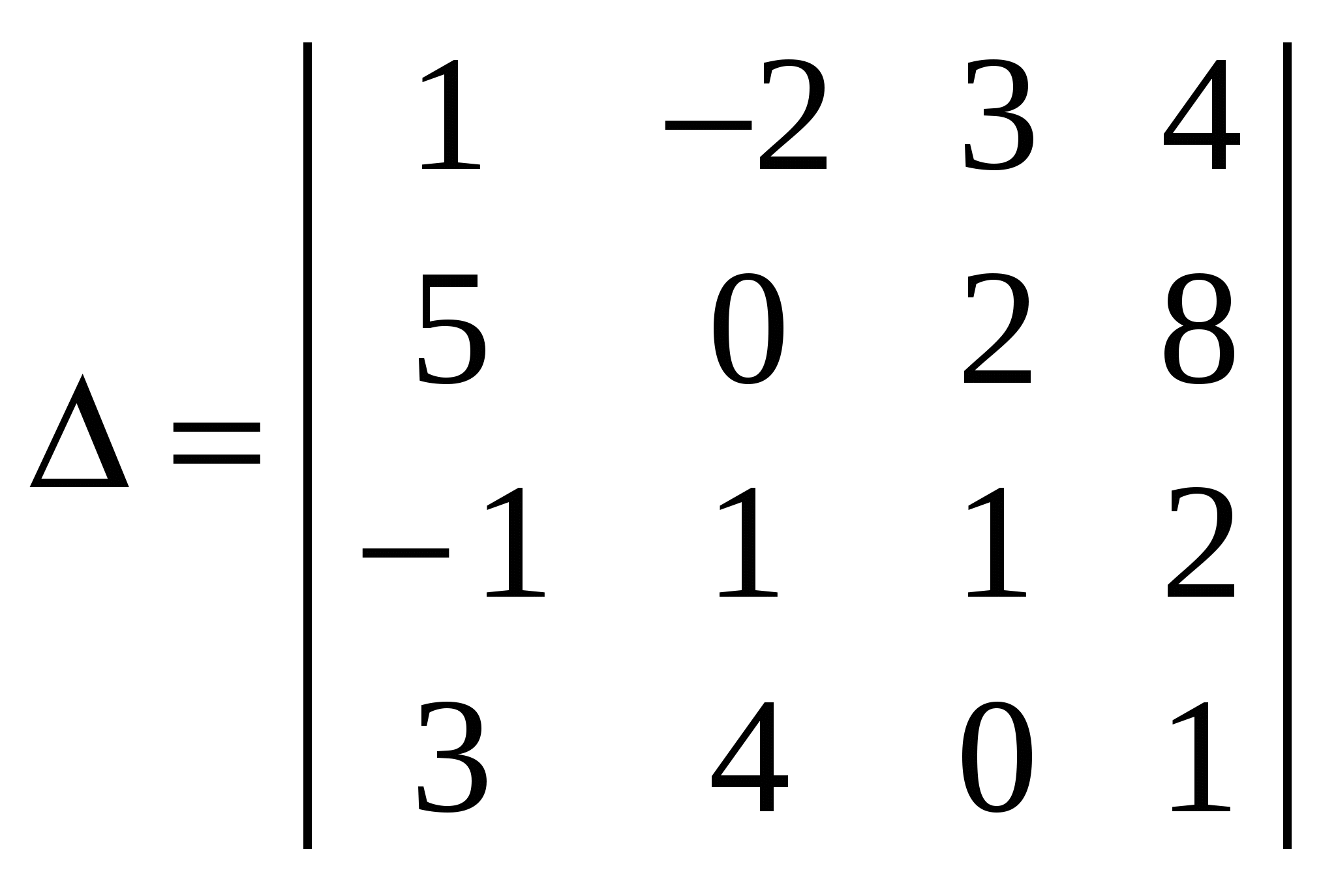 ; ; 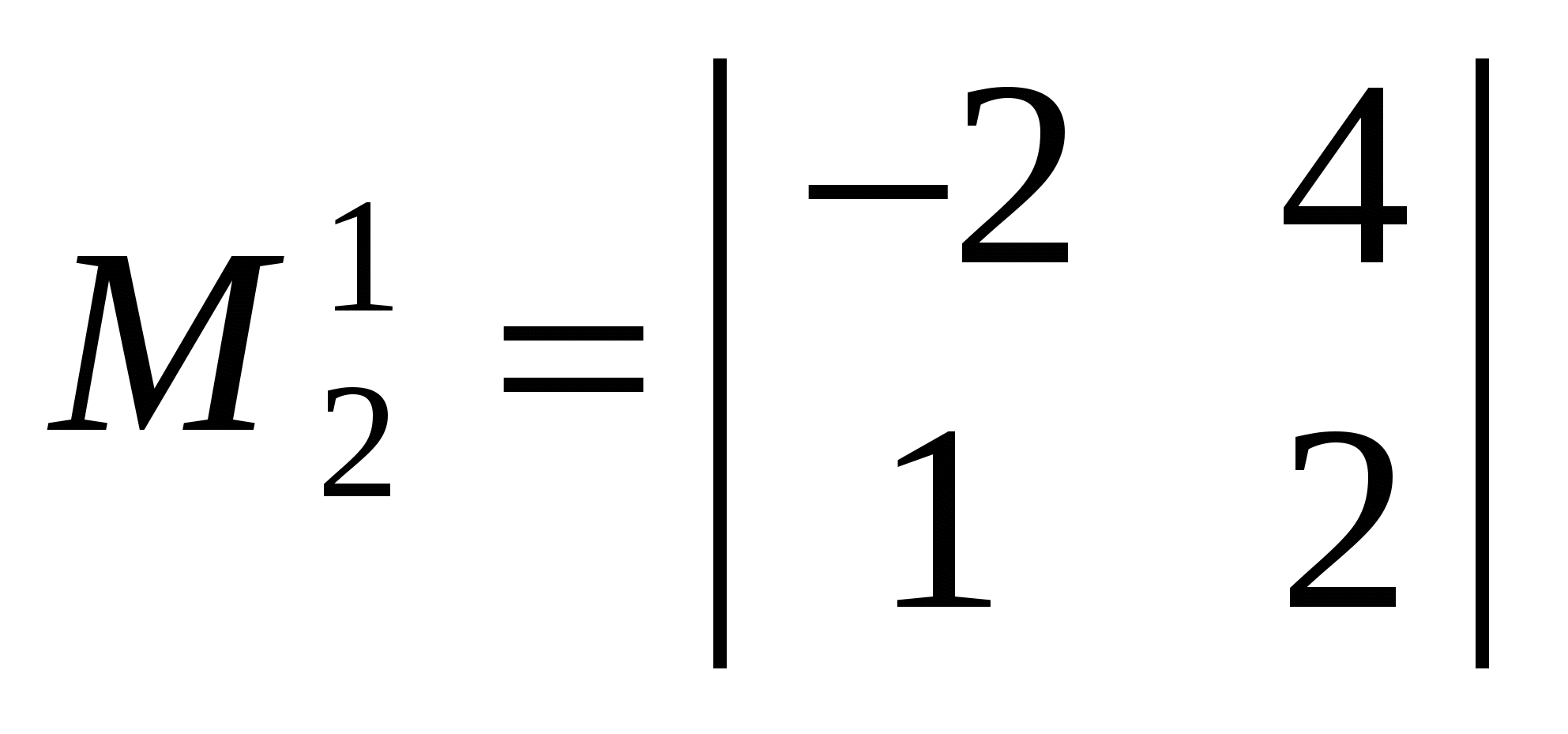 . .
Цей мінор утворено з елементів, які містяться на перетині першого і третього рядків та другого і четвертого стовпців. Викреслимо ці рядки та стовпці з визначника  дістанемо дістанемо 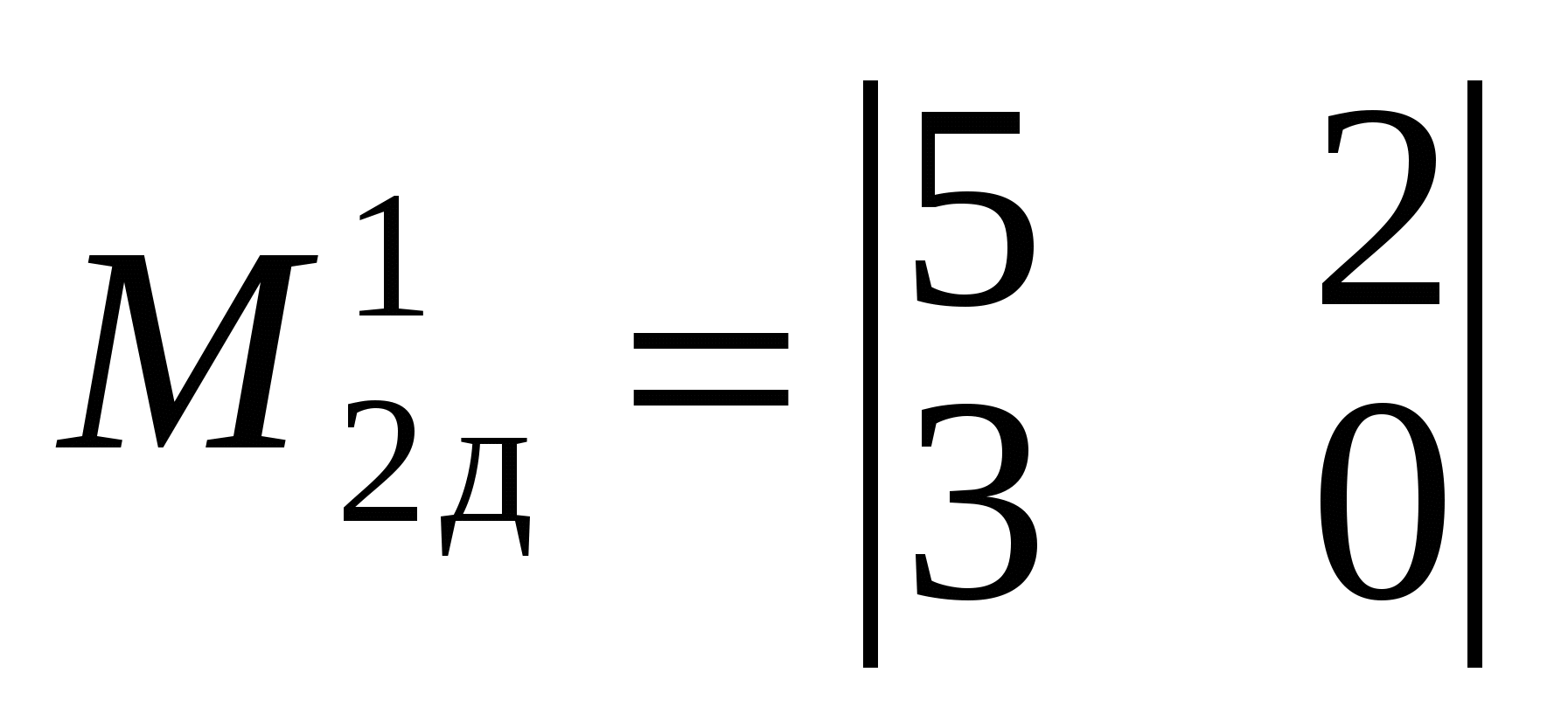 — мінор, доповняльний до мінора другого порядку — мінор, доповняльний до мінора другого порядку 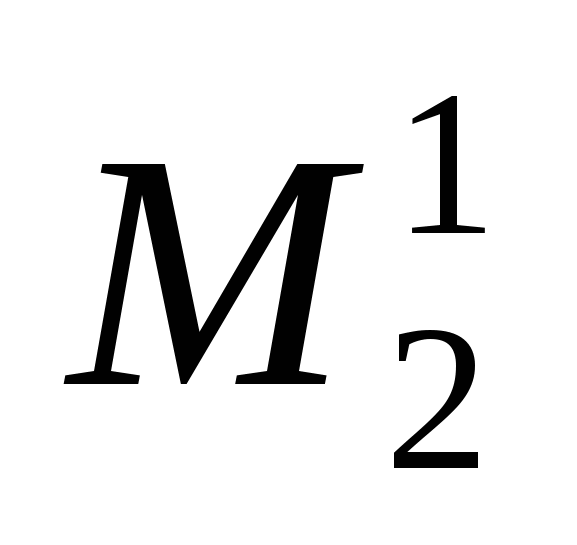 : :
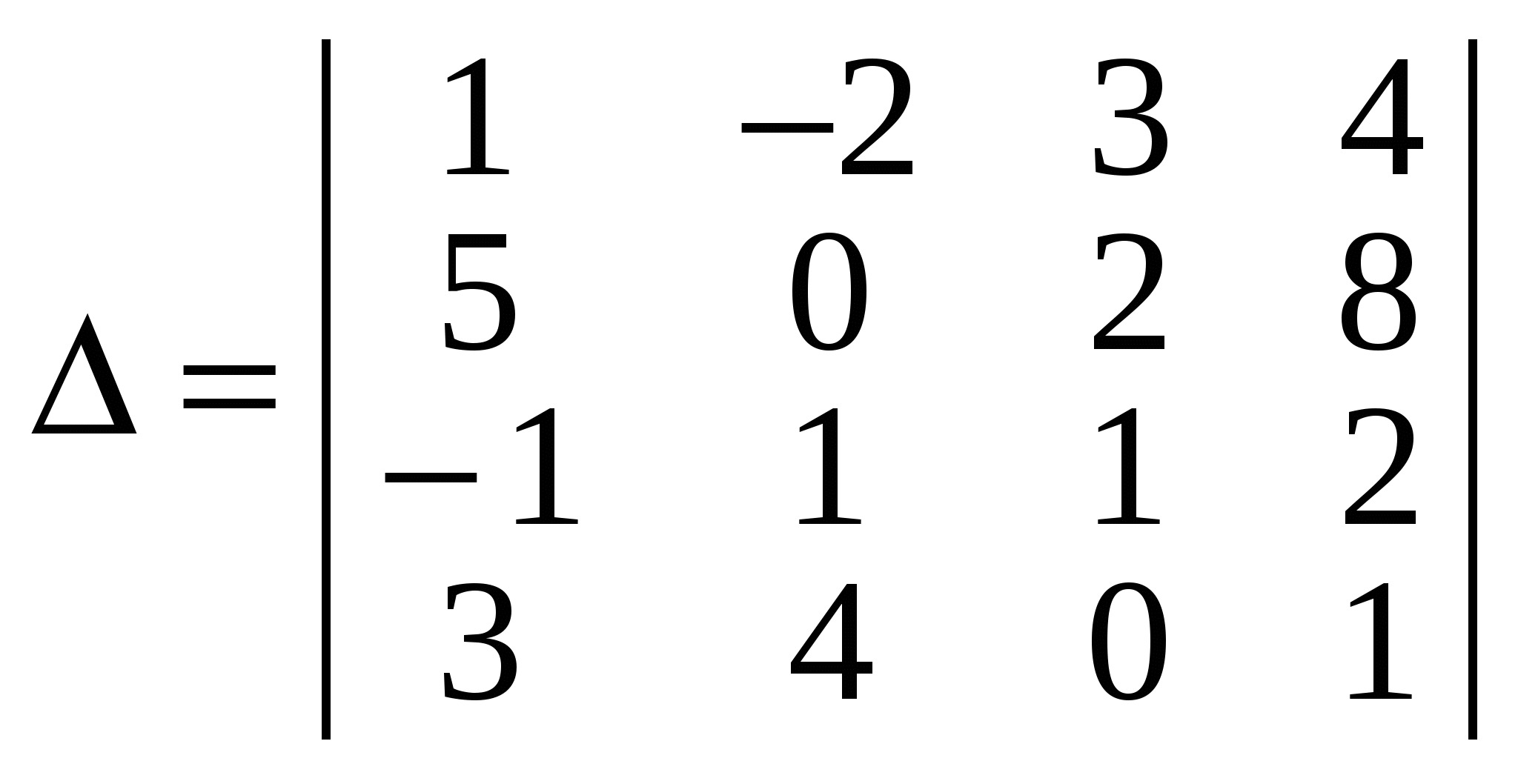  . .
Обчислити визначник
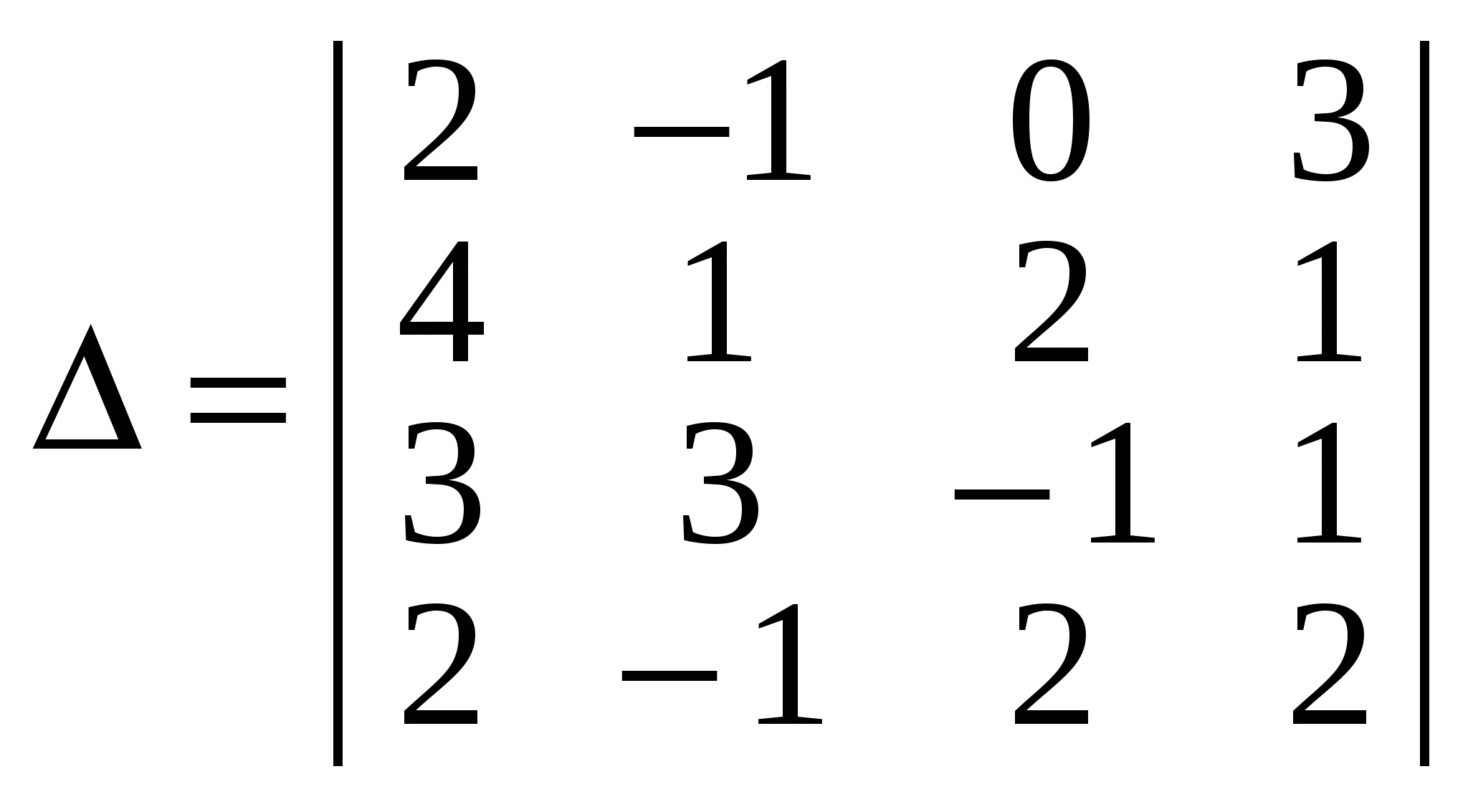 . .
Скориставшись означенням визначника, утворимо алгебраїчну суму добутків елементів, наприклад першого рядка, на їх
алгебраїчні доповнення:
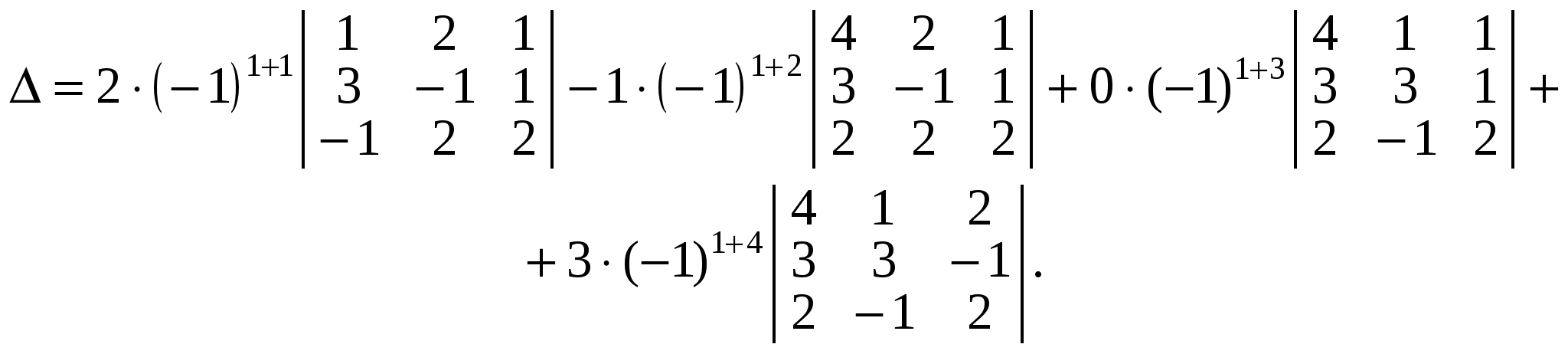
Отже, тепер потрібно обчислити три визначники третього порядку, оскільки визначник, який входить до третього доданка, обчислювати не потрібно. Зрозуміло, що чим більше нулів маємо в рядку або стовпці, за елементами якого утворюється алгебраїчна сума, тим менше визначників (n–1)-го порядку потрібно обчислювати.
Згідно з властивістю 8 утворимо в одному зі стовпців визначника  , наприклад в останньому, нулі. Якщо нулі утворюються в стовпці, використовуються елементи рядків, а якщо нулі утворюються в рядках, то навпаки — елементи стовпців. У четвертому стовпці є дві одиниці, одну з них візьмемо як розв’язувальний елемент і на підставі властивості 8 виконаємо перетворення: , наприклад в останньому, нулі. Якщо нулі утворюються в стовпці, використовуються елементи рядків, а якщо нулі утворюються в рядках, то навпаки — елементи стовпців. У четвертому стовпці є дві одиниці, одну з них візьмемо як розв’язувальний елемент і на підставі властивості 8 виконаємо перетворення:
елементи третього (робочого) рядка перепишемо у перетворюваний визначник без змін;
помножимо всі елементи третього рядка на –3, додамо до відповідних елементів першого рядка, а результат запишемо в перший рядок;
помножимо всі елементи третього рядка на –1, додамо до відповідних елементів другого рядка, а результат запишемо у другий рядок;
помножимо всі елементи третього рядка на –2, додамо до відповідних елементів четвертого рядка, а результат запишемо в четвертий рядок.
Після цих перетворень значення визначника не зміниться, але він набере такого вигляду:
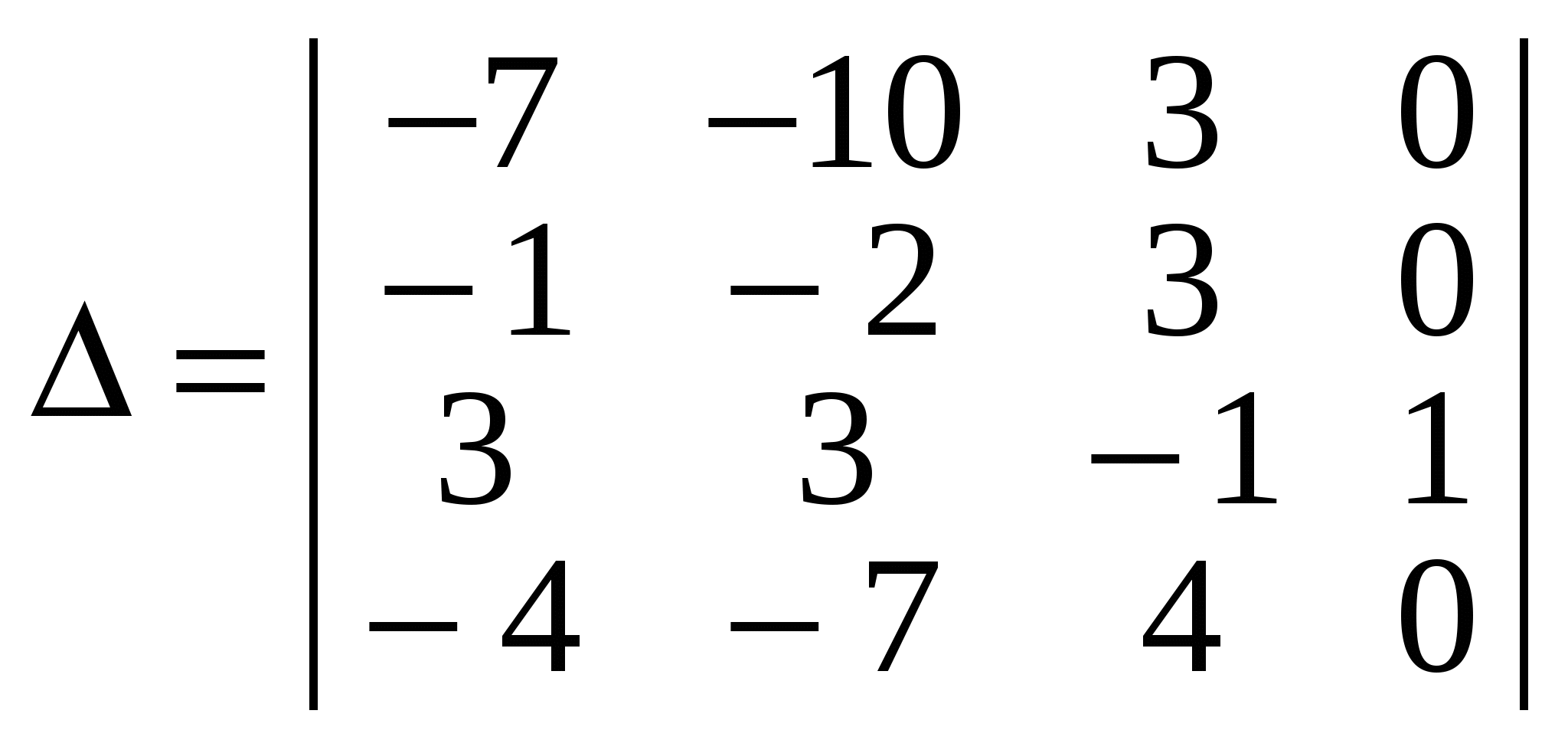 . .
Тепер, скориставшись означенням визначника і розклавши його за елементами четвертого стовпця, дістанемо:
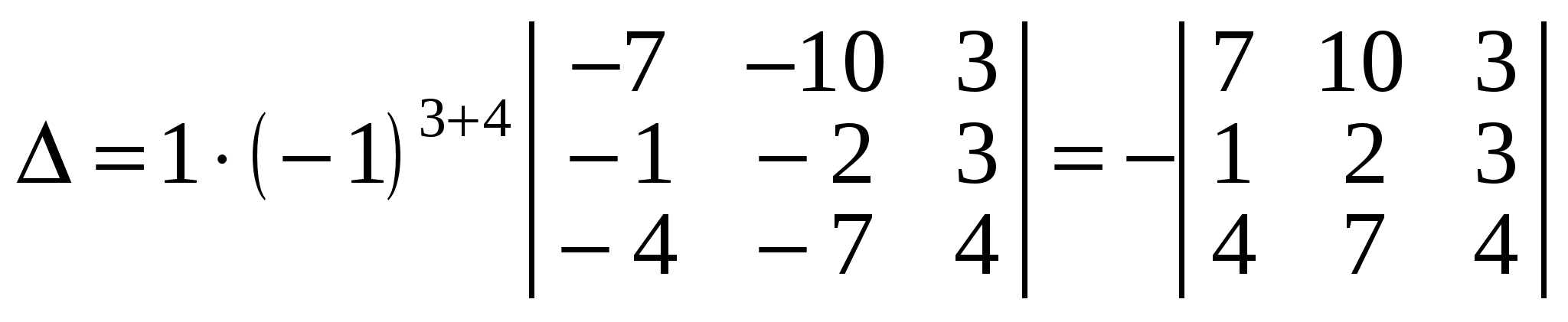 . .
Останній визначник записано згідно з властивістю 5, і тепер обчислення визначника четвертого порядку звелось до обчислення одного визначника третього порядку. Його можна обчислити за означенням, а можна знову утворити нулі, скажімо, у другому рядку, скориставшись одиницею як розв’язувальним елементом і виконавши дії згідно з властивістю 8 зі стовпцями. Дістанемо:
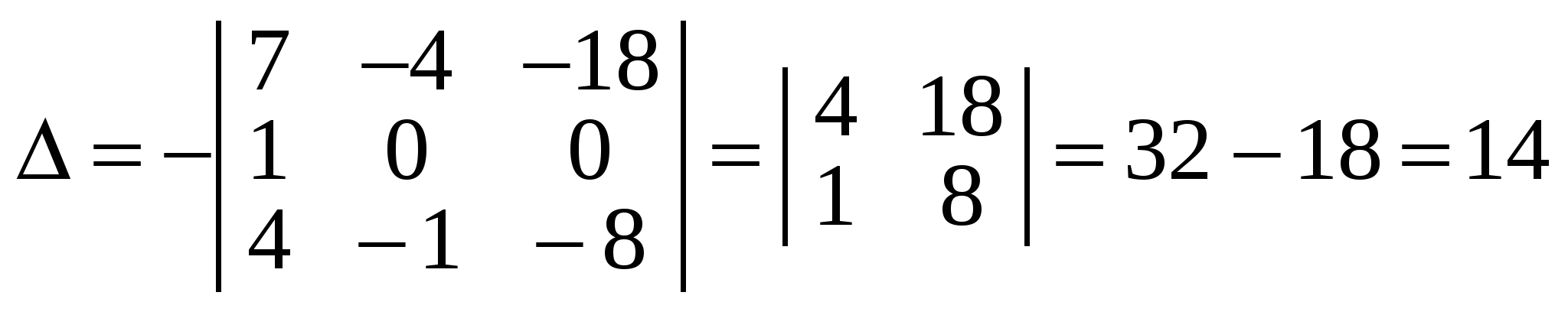 . .
Зрозуміло, що за такою схемою можна обчислити визначник будь-якого порядку.
Розв’язати систему рівнянь:
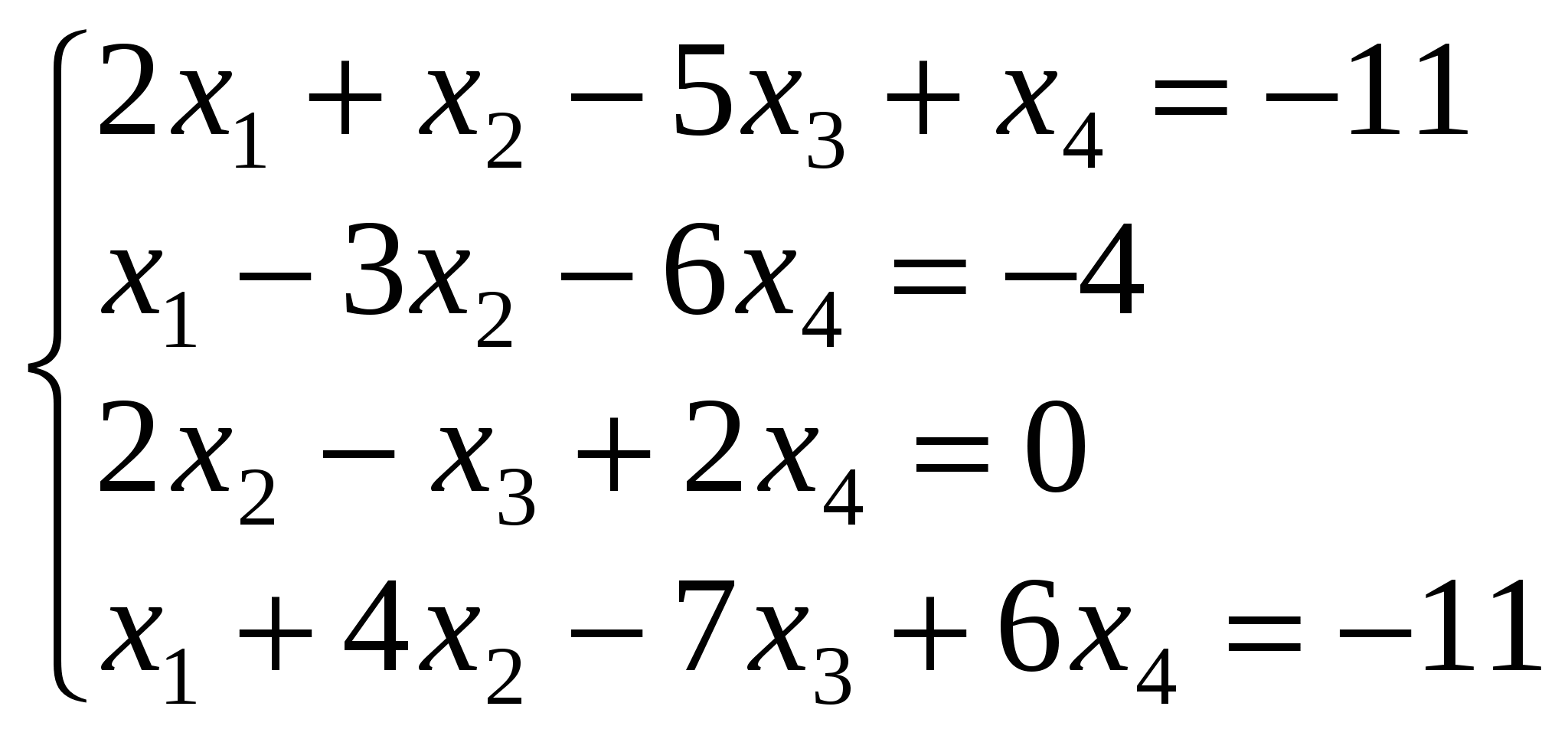
Складемо й обчислимо спочатку головний визначник цієї системи: 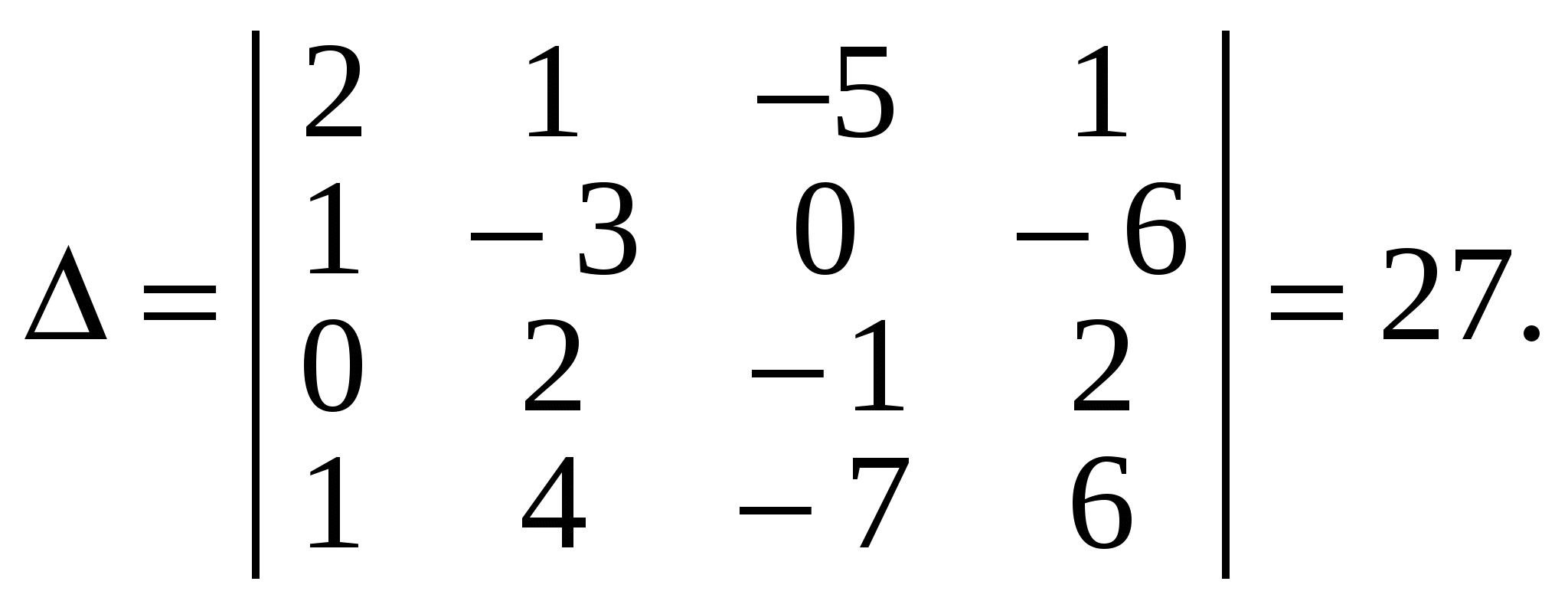 Отже, головний визначник системи рівнянь відмінний від нуля. За правилом Крамера така система має єдиний розв’язок. Знайдемо його. Для цього утворимо і обчислимо ще чотири визначники: Отже, головний визначник системи рівнянь відмінний від нуля. За правилом Крамера така система має єдиний розв’язок. Знайдемо його. Для цього утворимо і обчислимо ще чотири визначники:

За правилом Крамера маємо розв’язки:
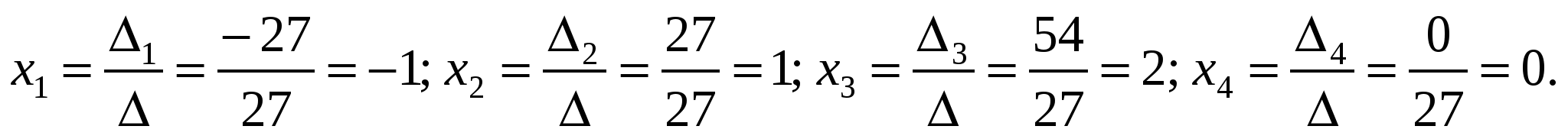
Отже, 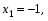 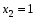 , , 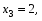 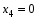 — єдиний розв’язок. — єдиний розв’язок.
Завдання для перевірки знань
Скориставшись правилом обчислення визначників 3-го порядку, довести властивості 1—8.
Скориставшись властивостями визначників, обчислити:
а)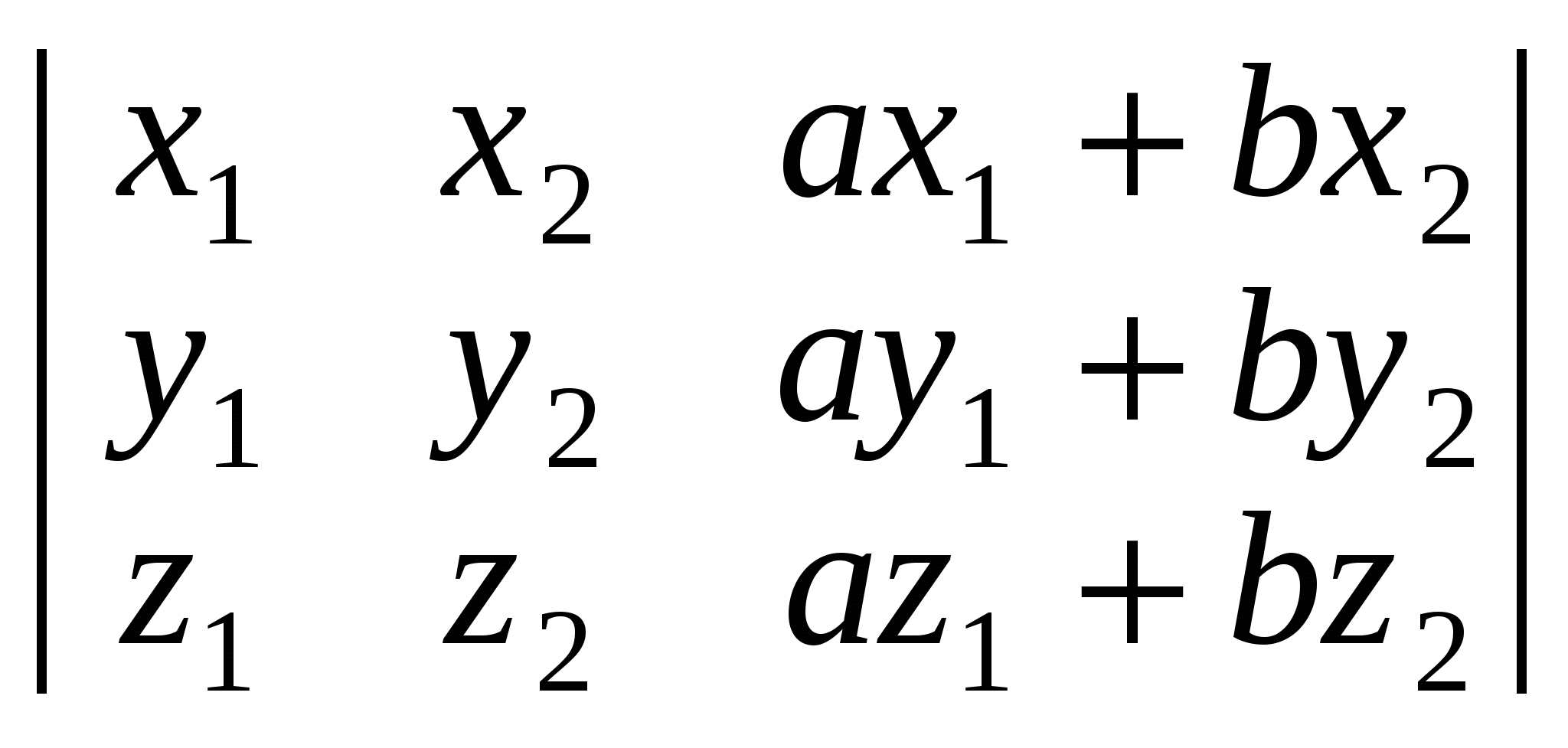 ; б) ; б)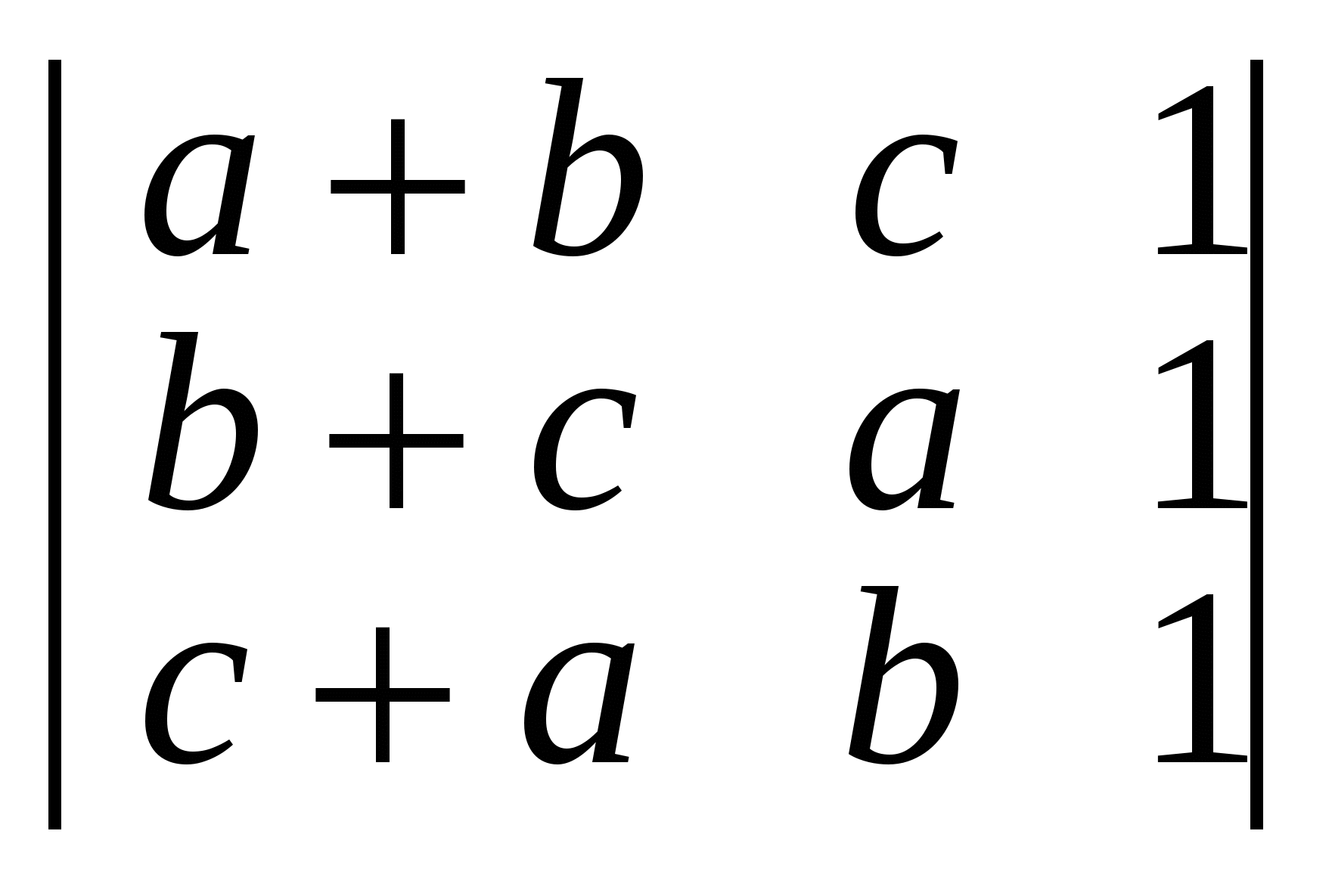 ; ; 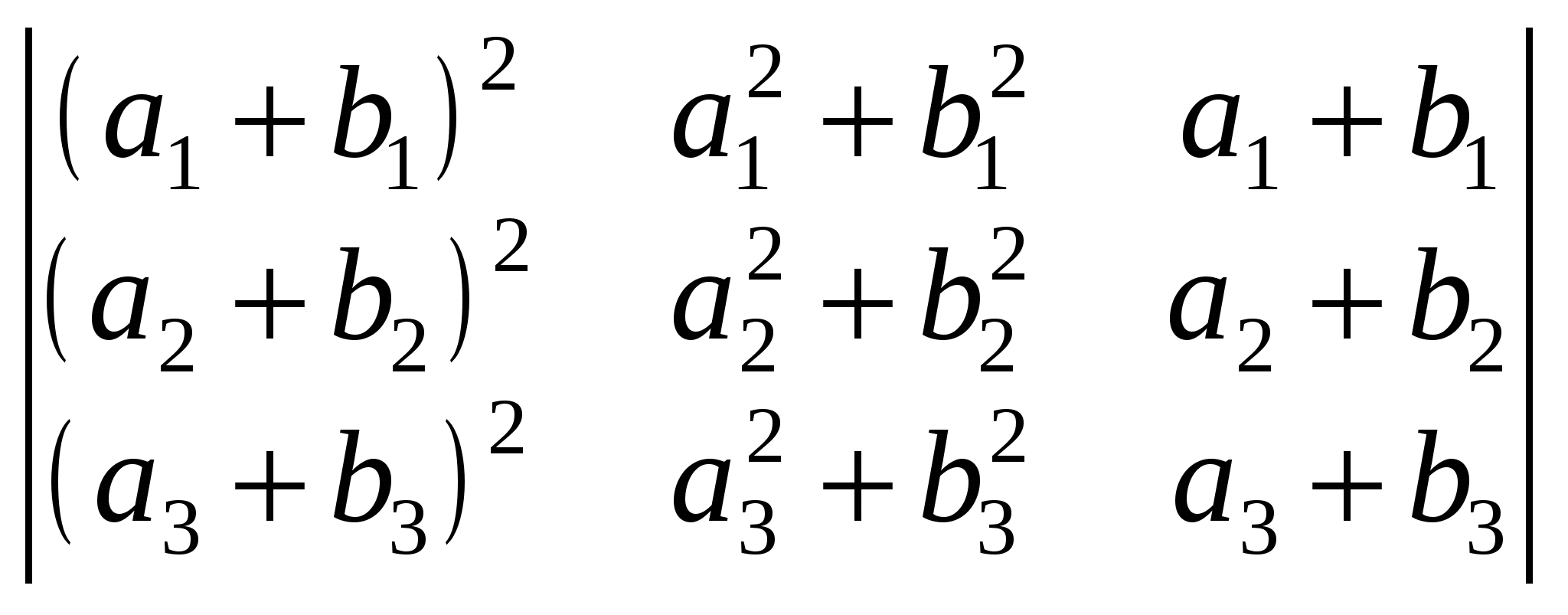 . .
Відповідь. а) 0; б) 0; в) 0.
3. Скориставшись властивостями визначників, довести тотожності:
а) 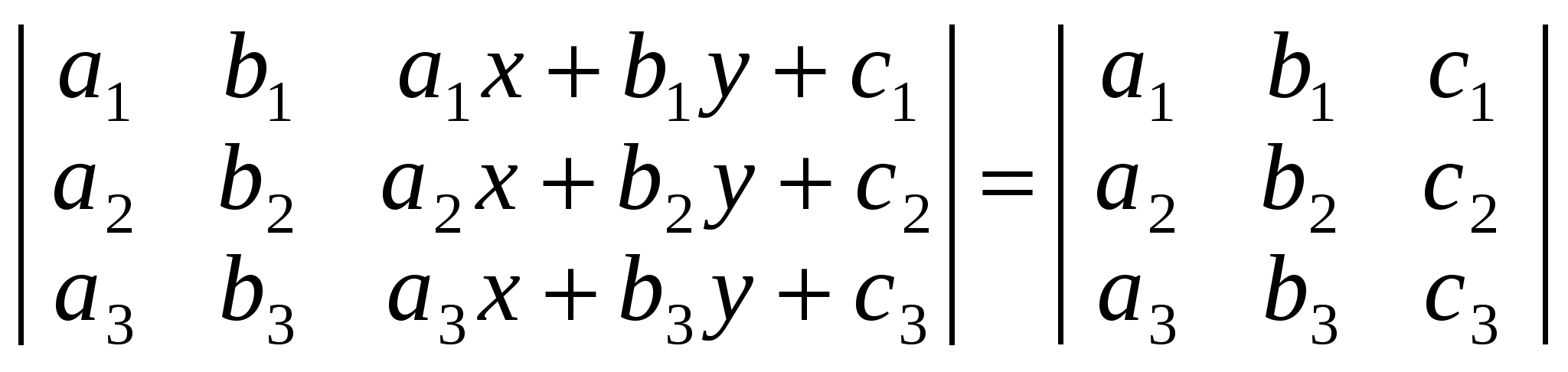 ; ;
б) 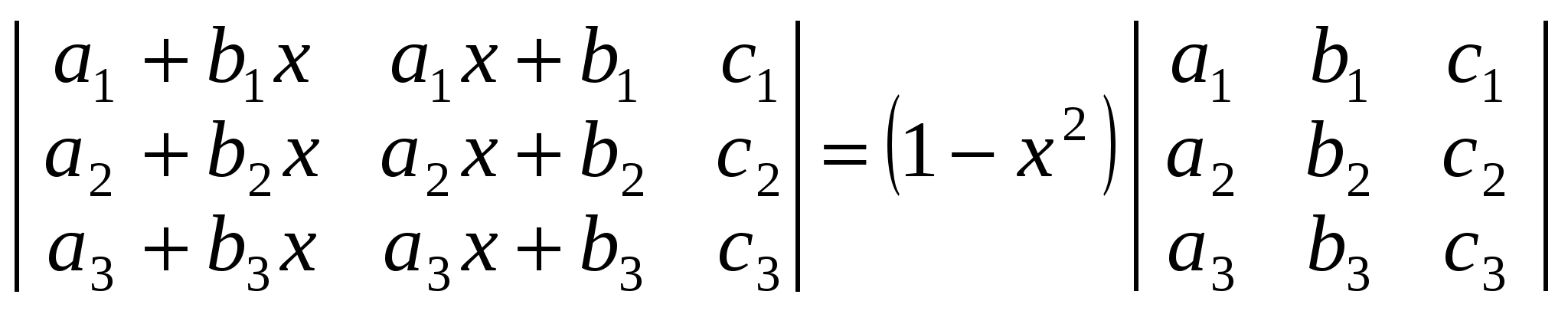 ; ;
в) 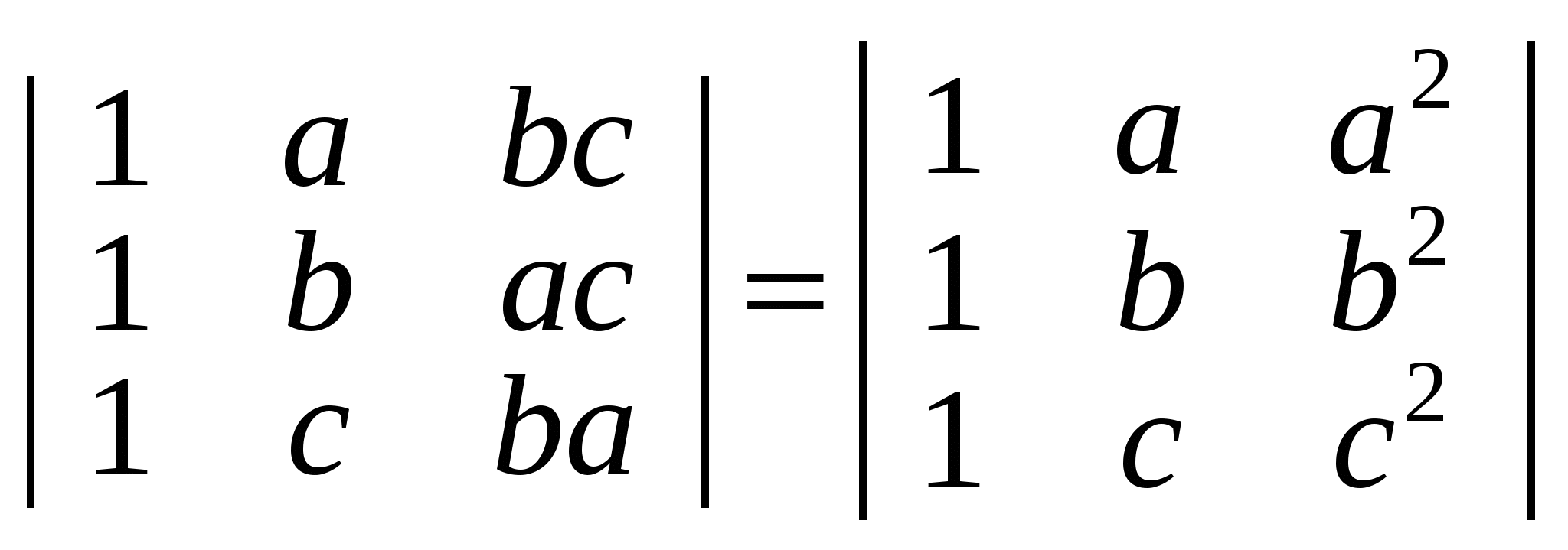 . .
Розклавши визначник за рядком або стовпцем, що складається лише з букв, обчислити:
а)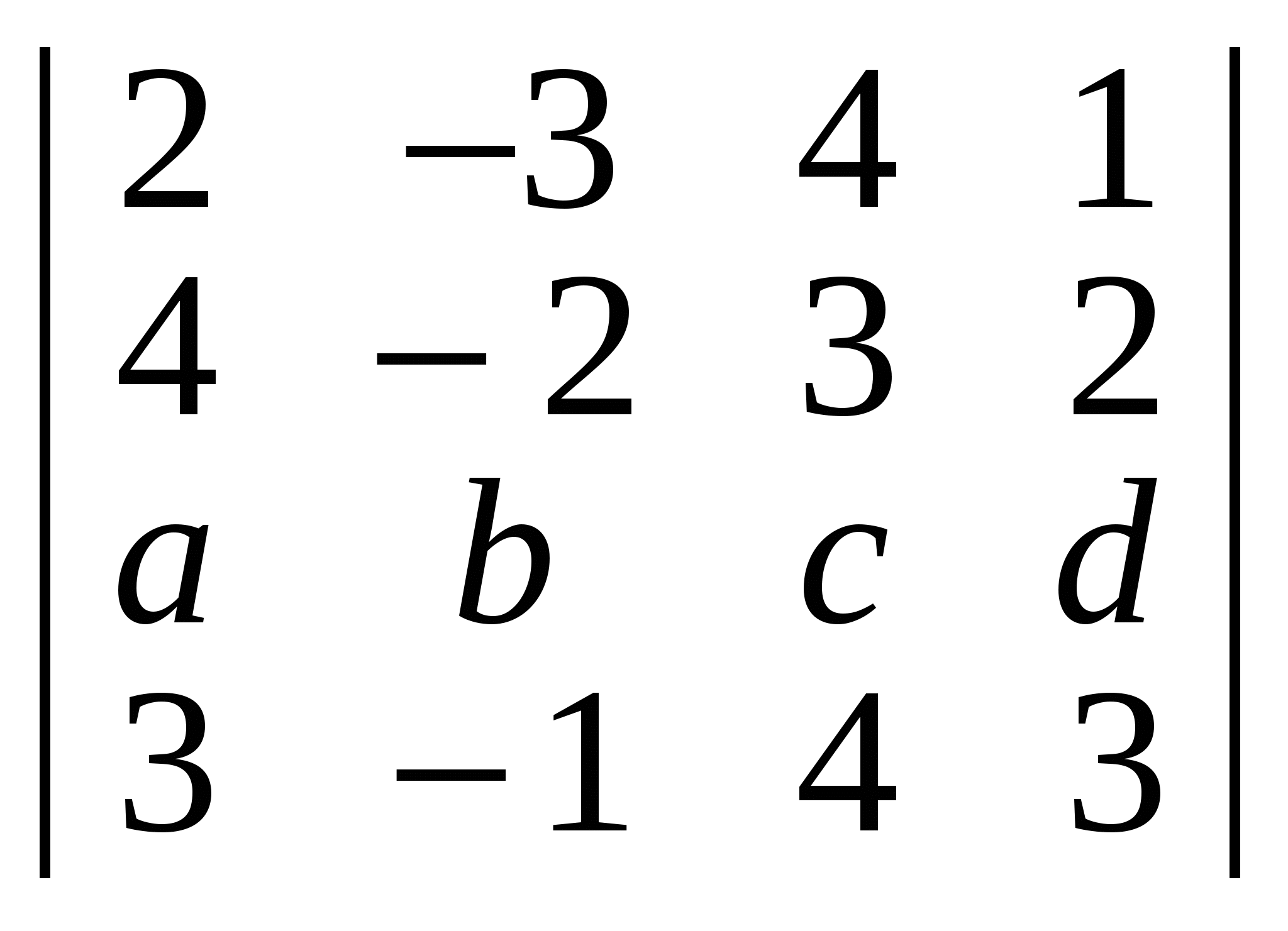 ; б) ; б)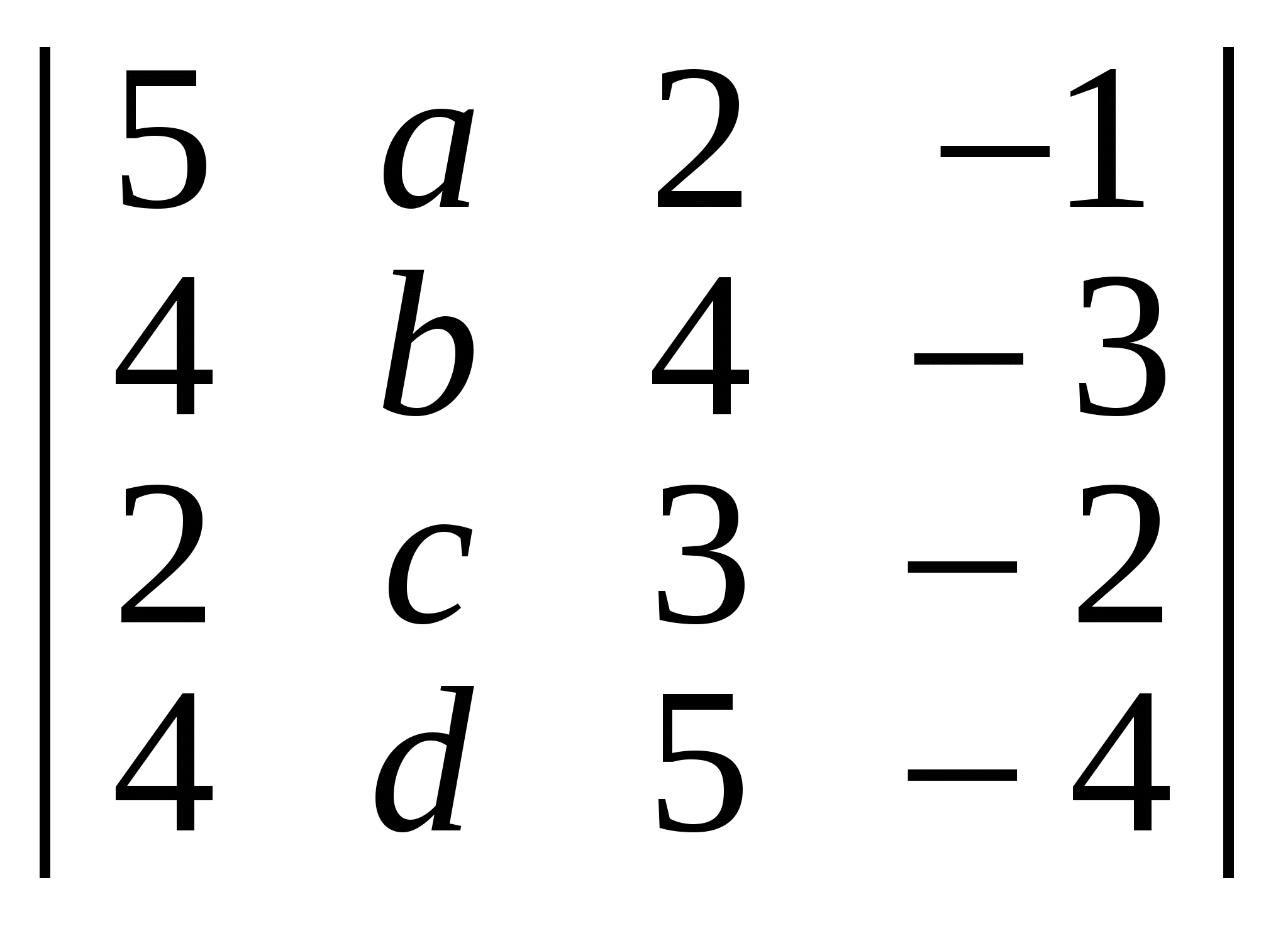 ; в) ; в) 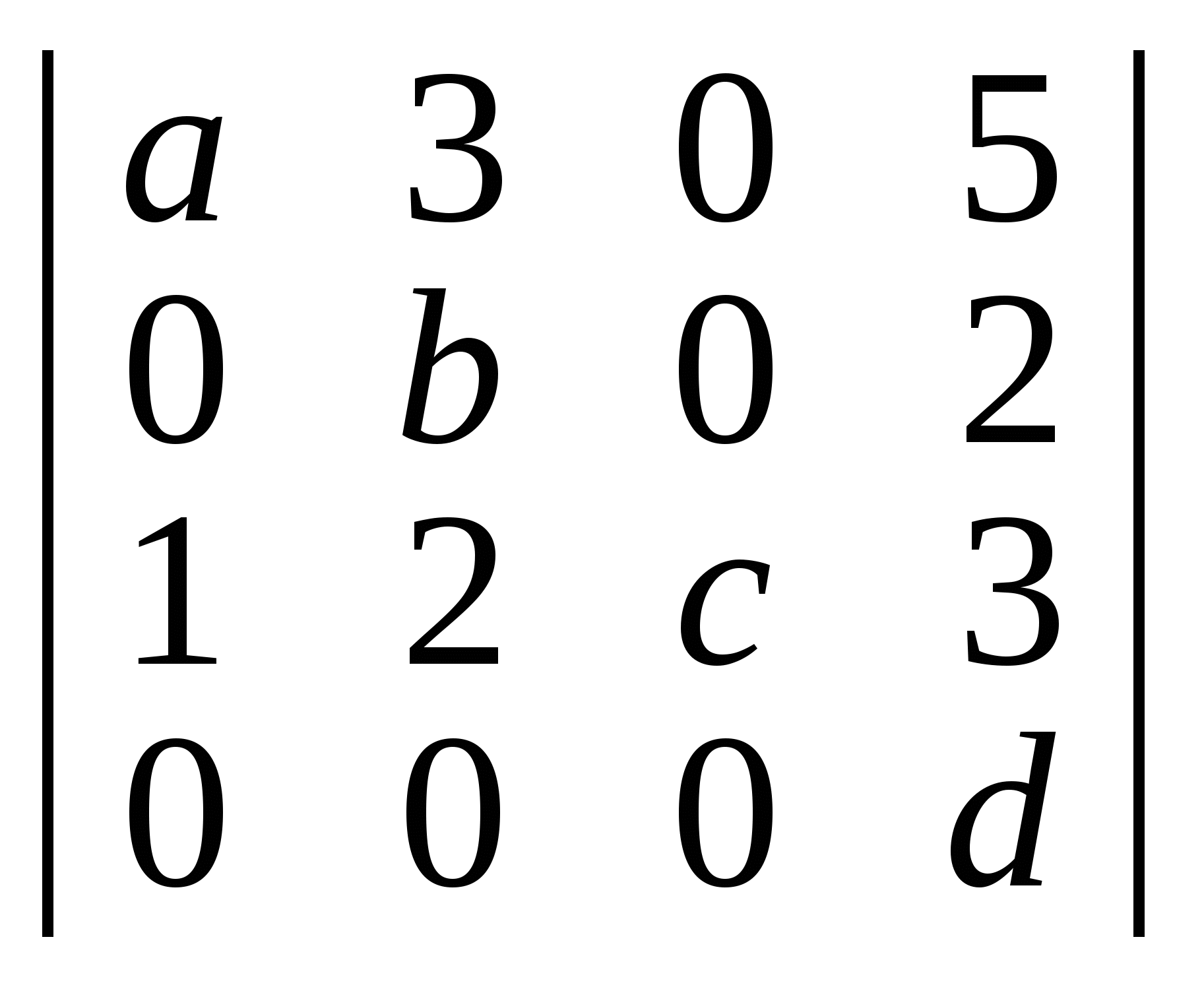 . .
Відповідь. а) 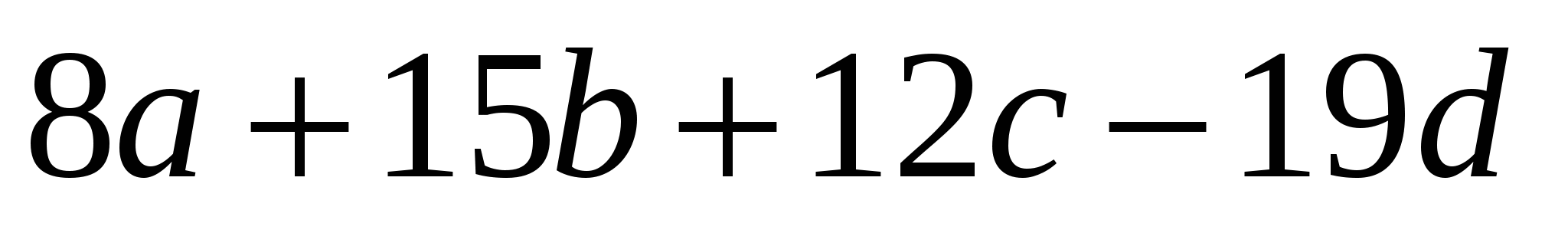 ; б) ; б) 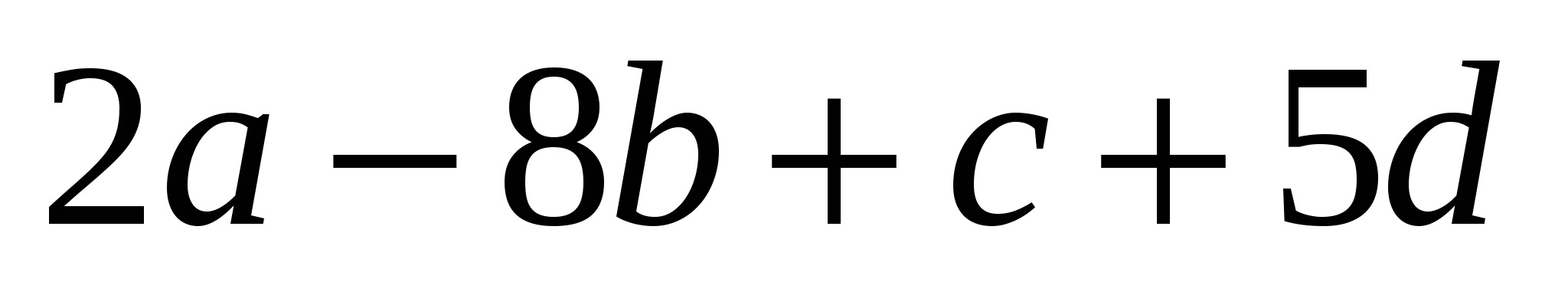 ; в) ; в)  . .
Обчислити визначники:
а)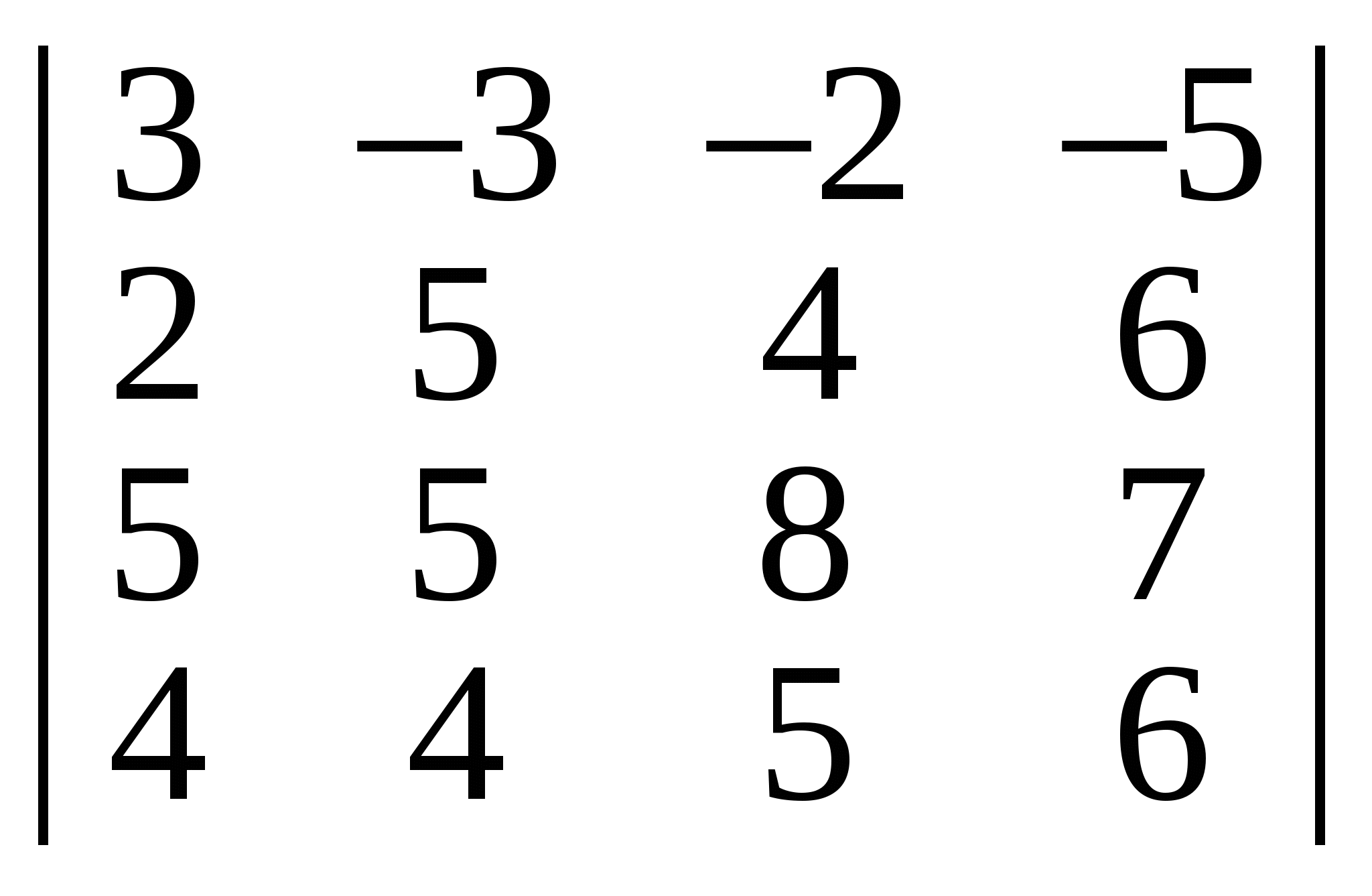 ; б) ; б)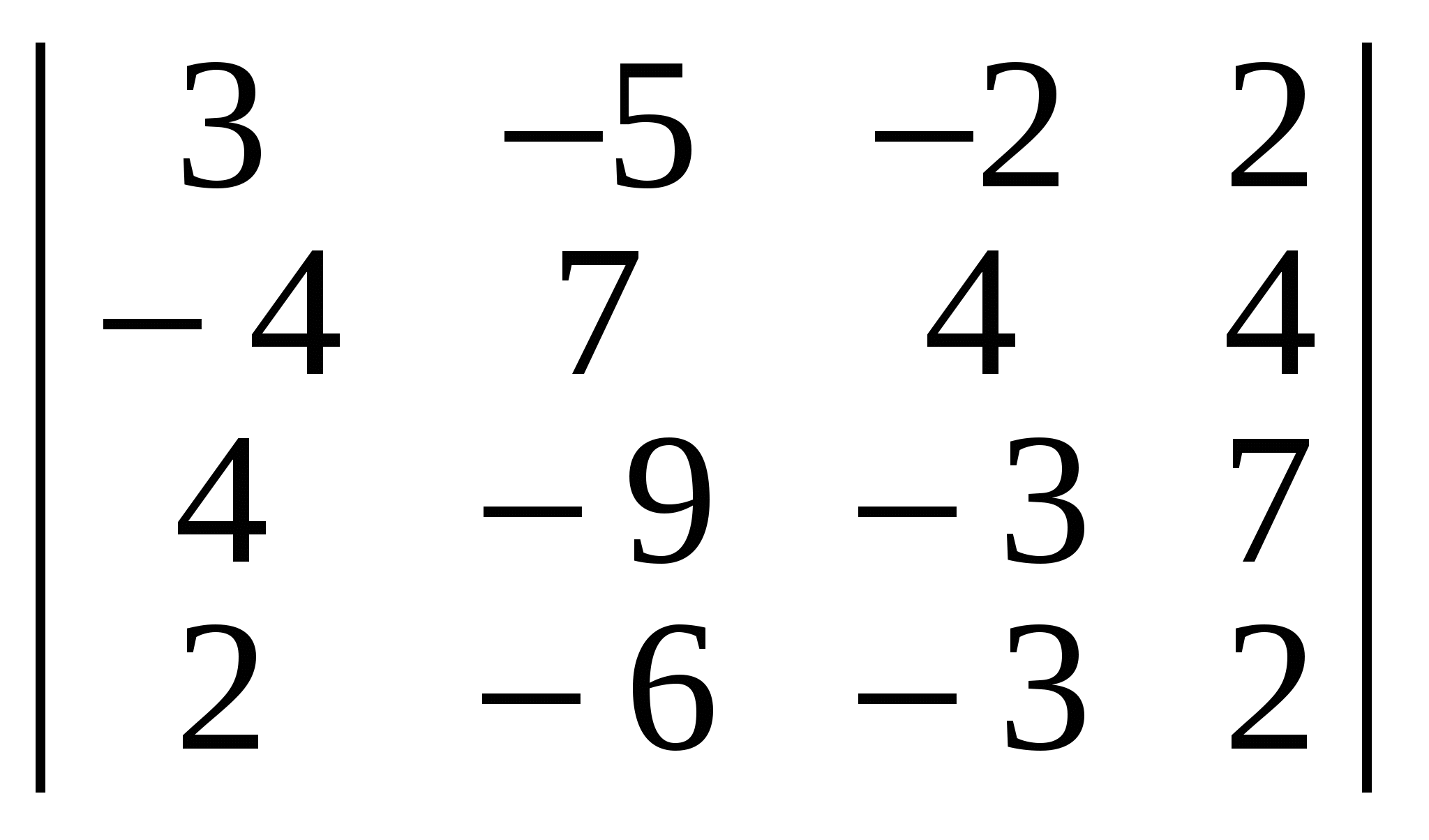 ; в) ; в)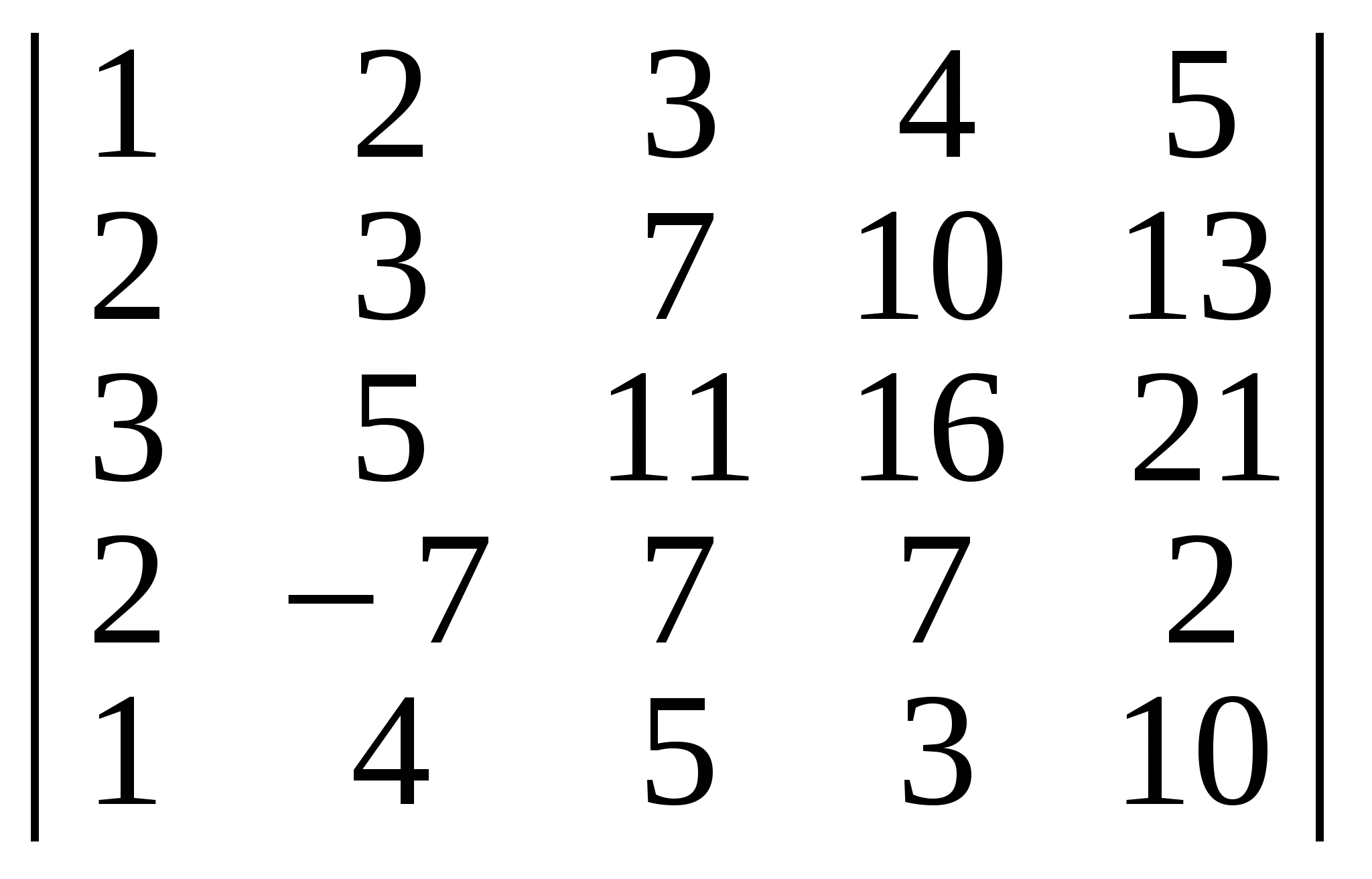 ; ;
г)  ; д) ; д)  . .
Відповідь. а) 90; б) 27; в) 52; г) 10; д) 100.
6. Розв’язати за правилом Крамера системи рівнянь:
а)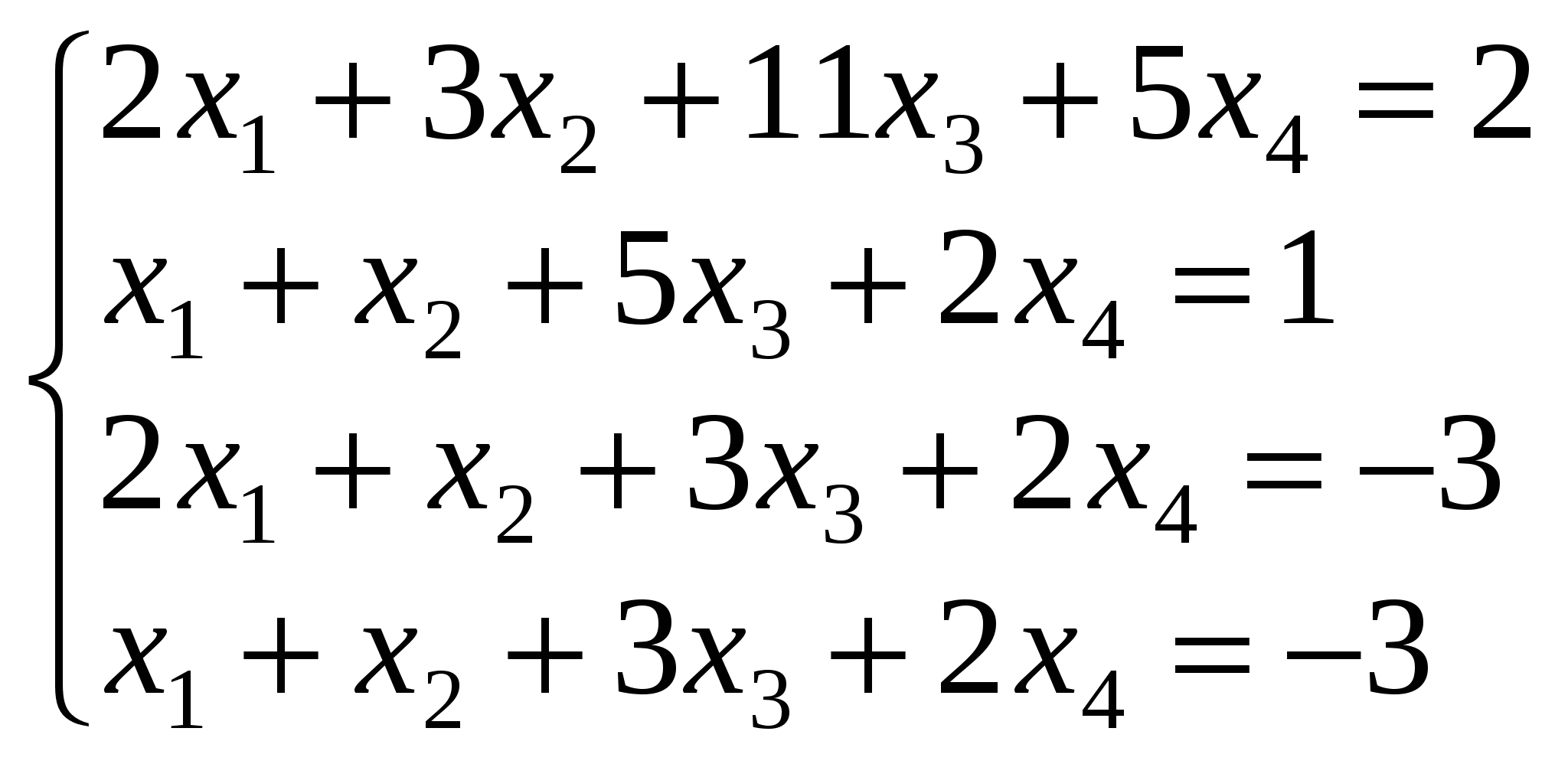 ; б) ; б)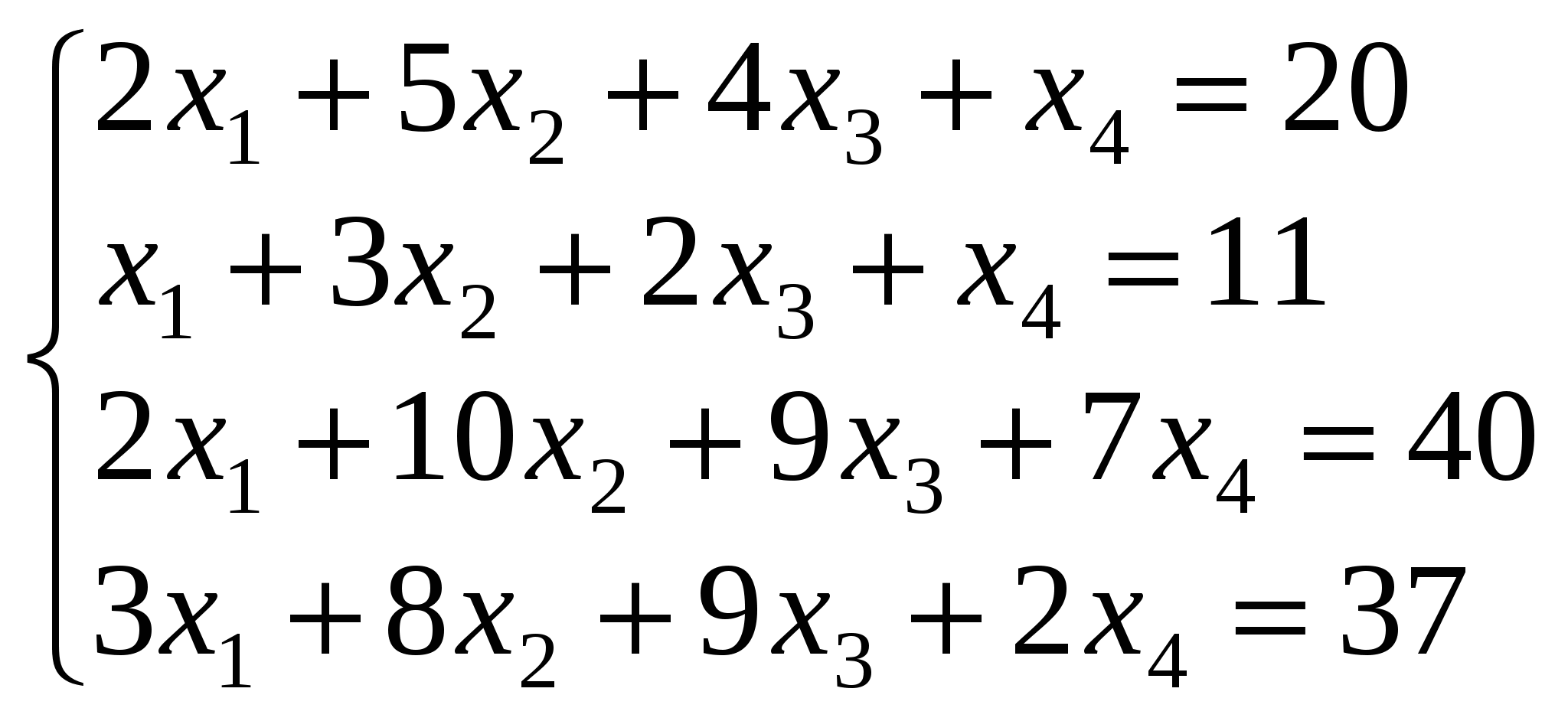 ; ;
в) 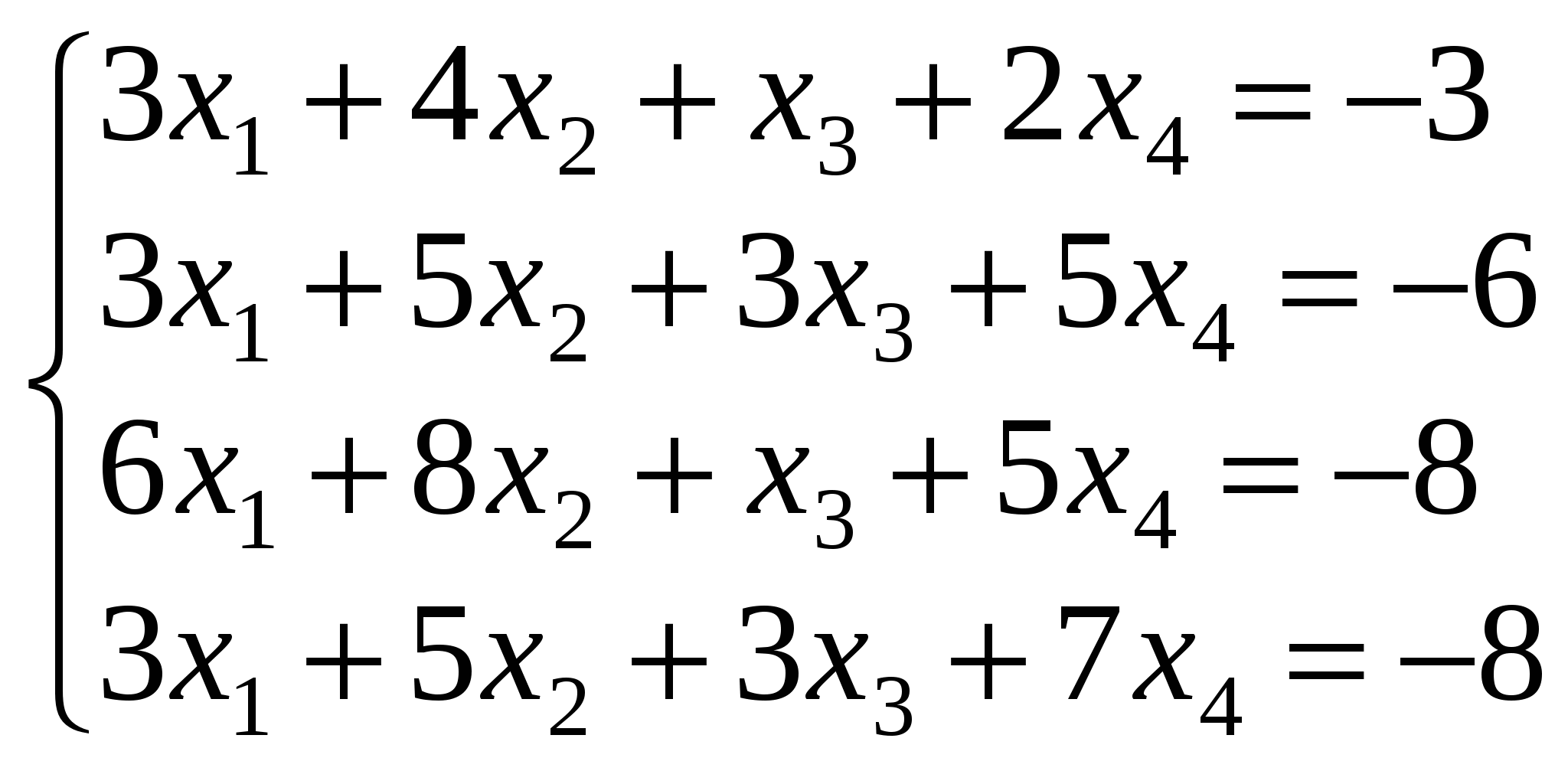 ; г) ; г) 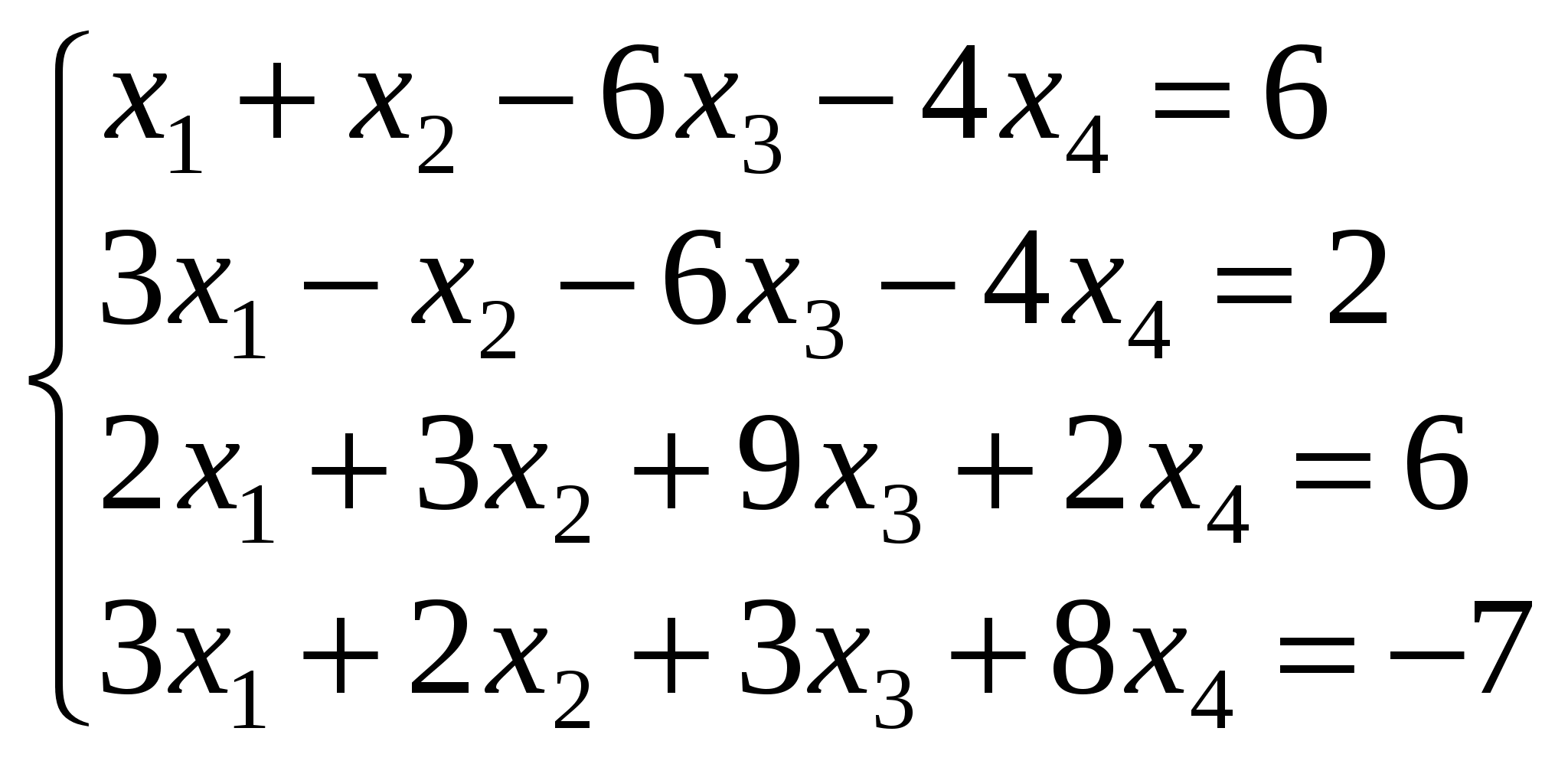 . .
Відповідь. а) 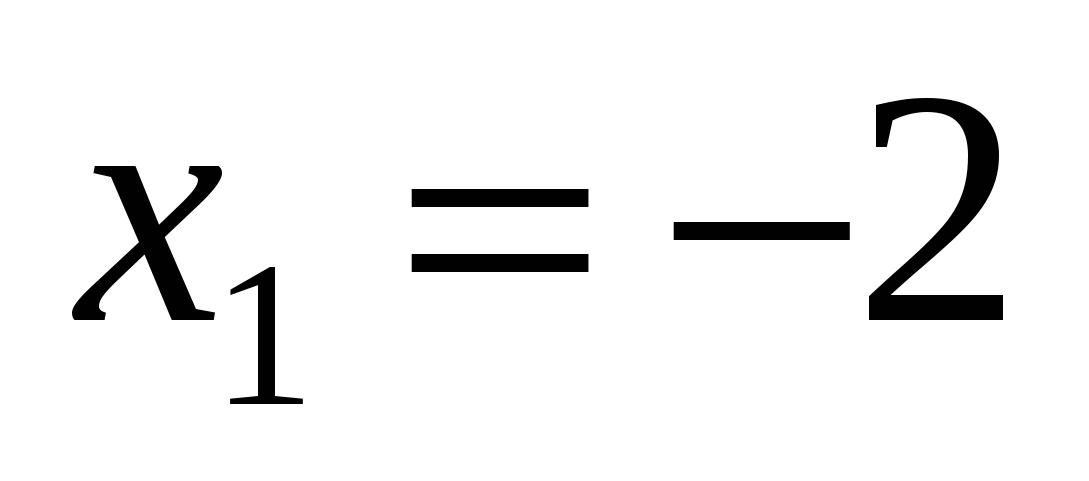 , , 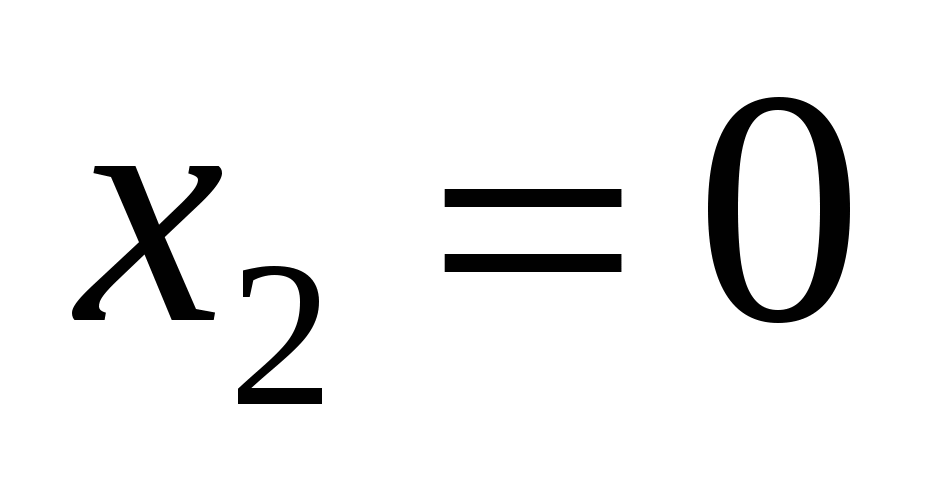 , , 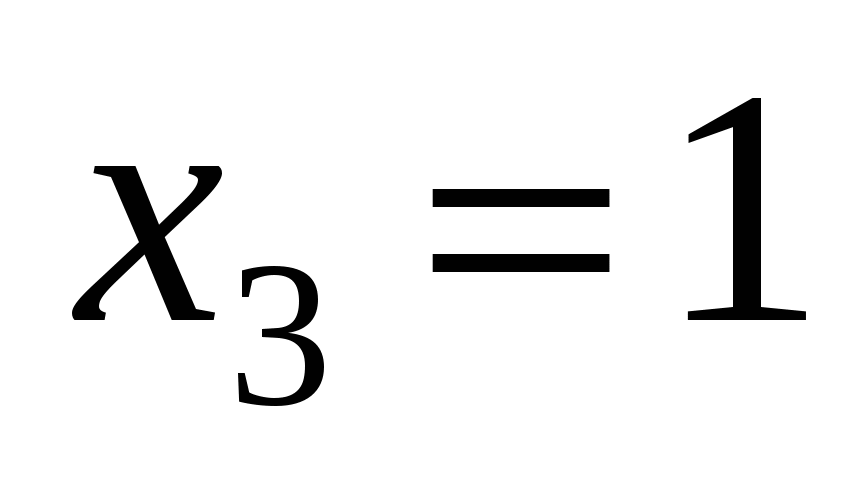 , , 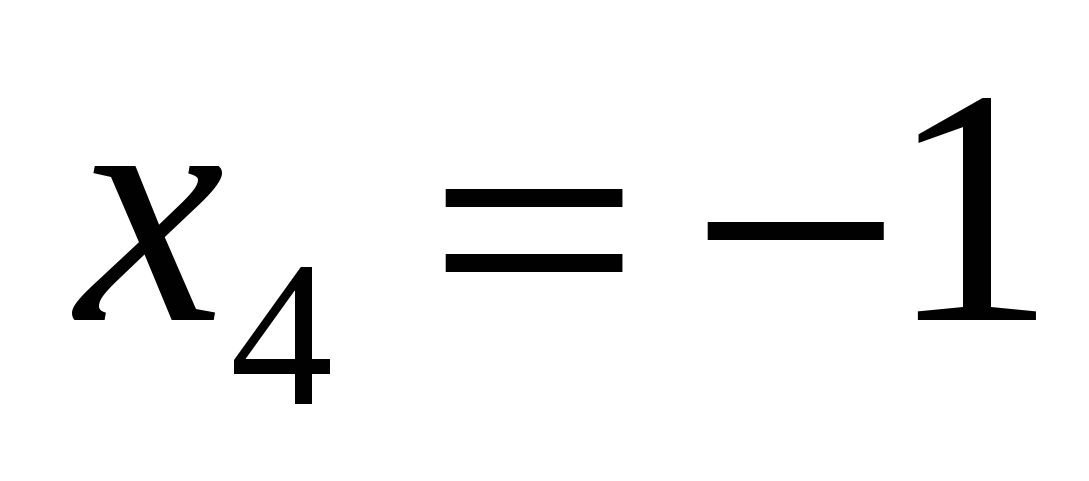 ; б) ; б) 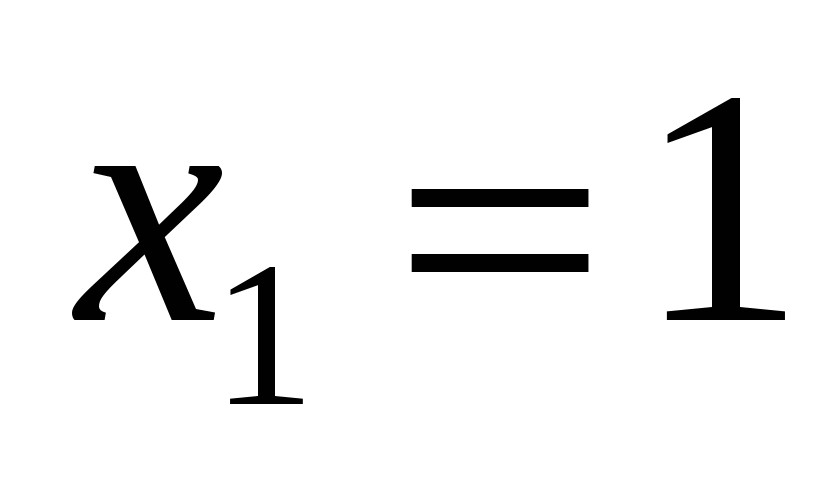 , ,  , , 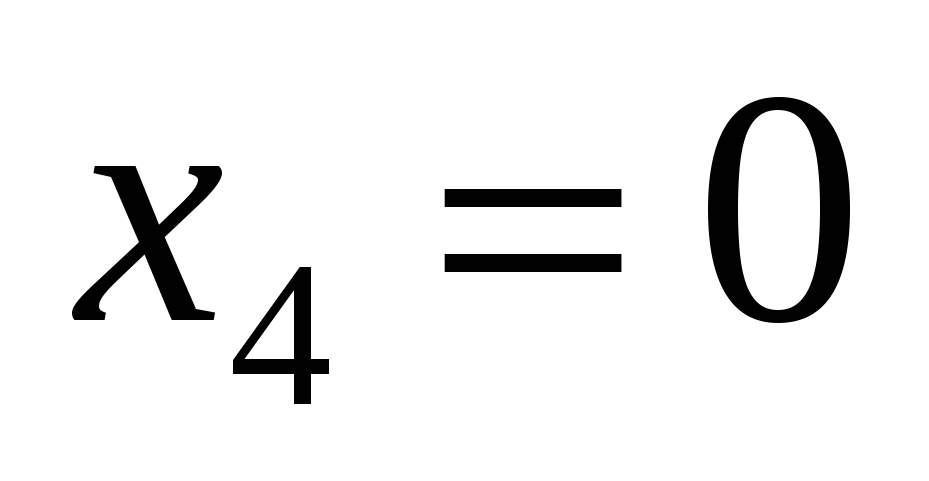 ; в) ; в) 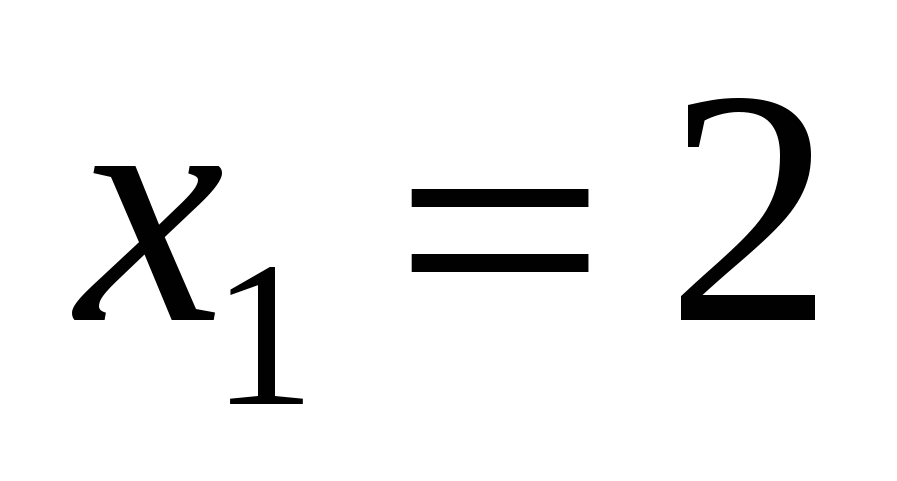 , , 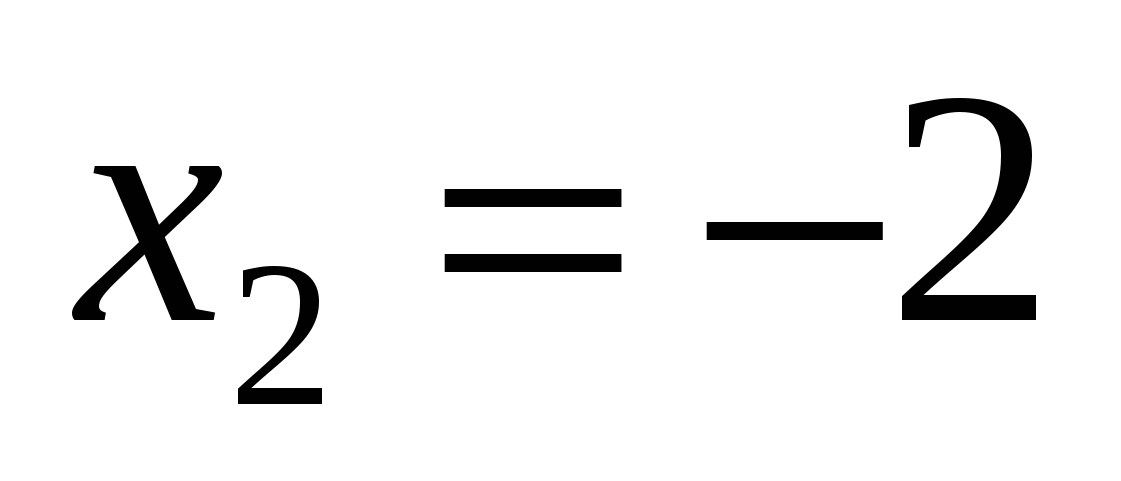 , , 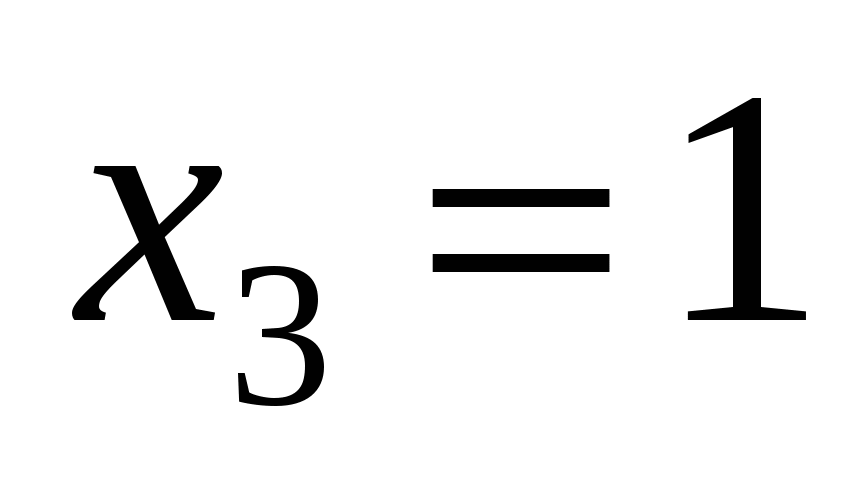 , , 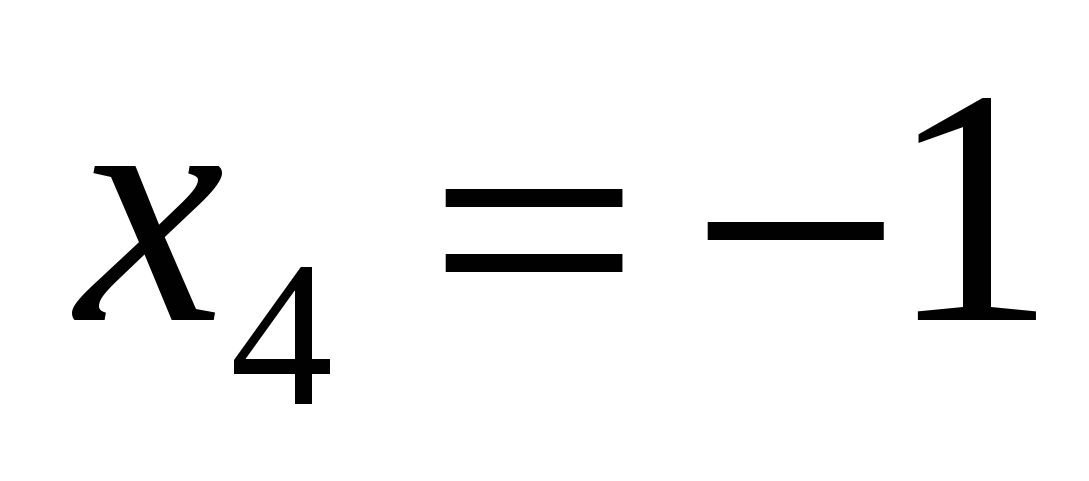 ; г) ; г)  , , 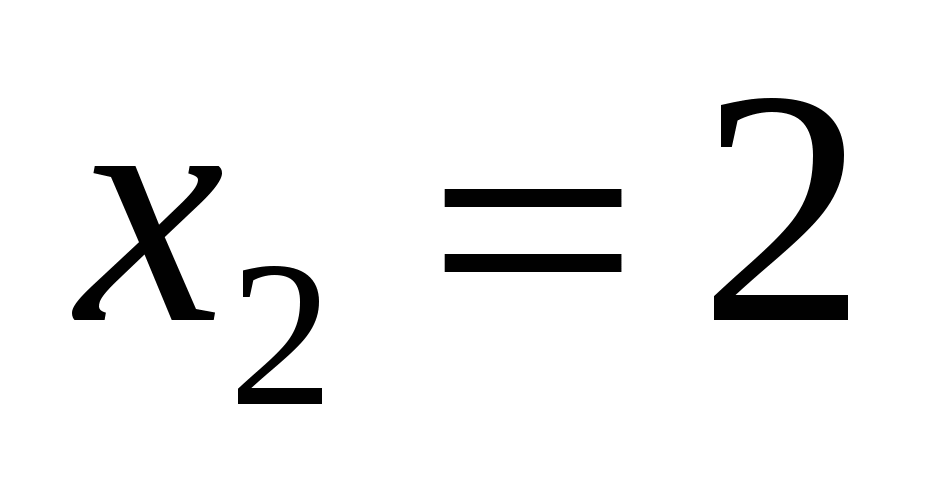 , , 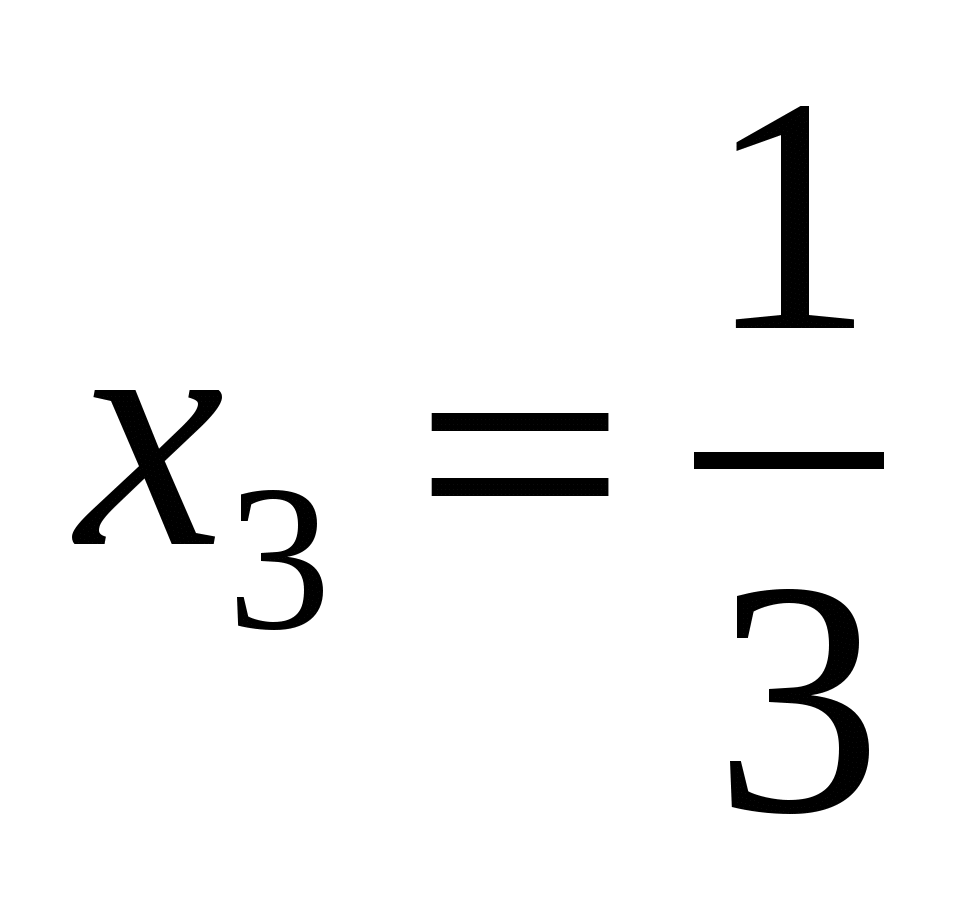 , , 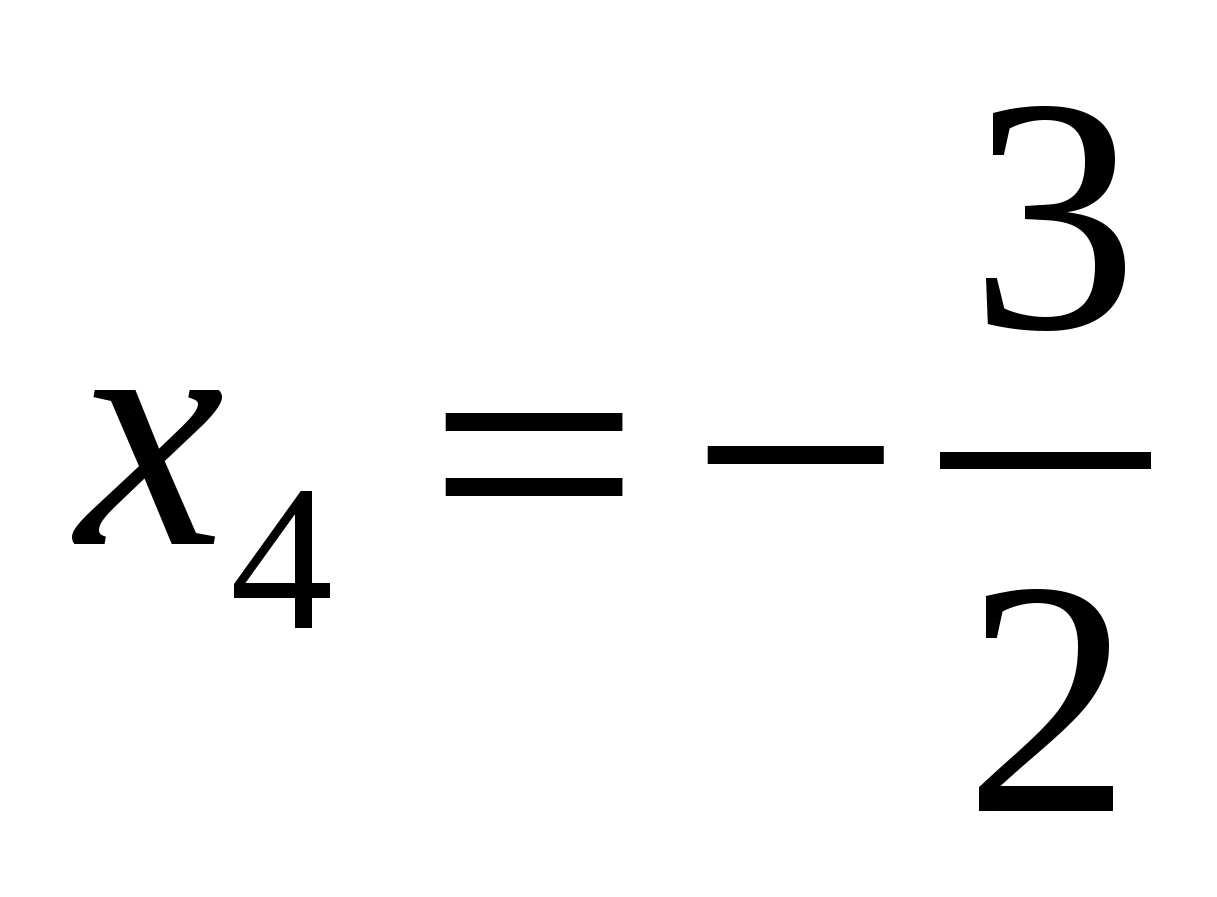 . .
Побудувати всі можливі мінори другого порядку визначника:
а) 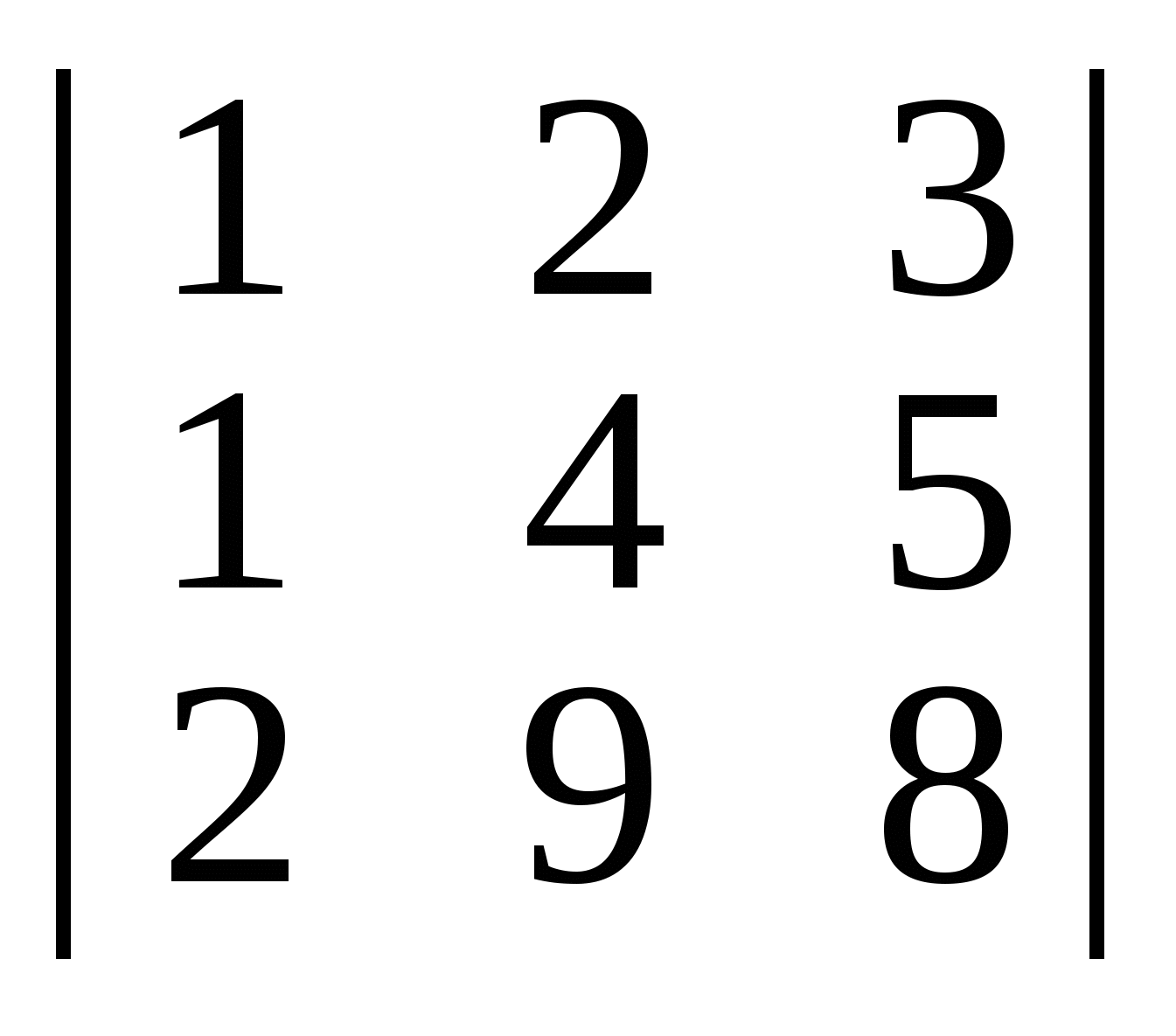 ; б) ; б) 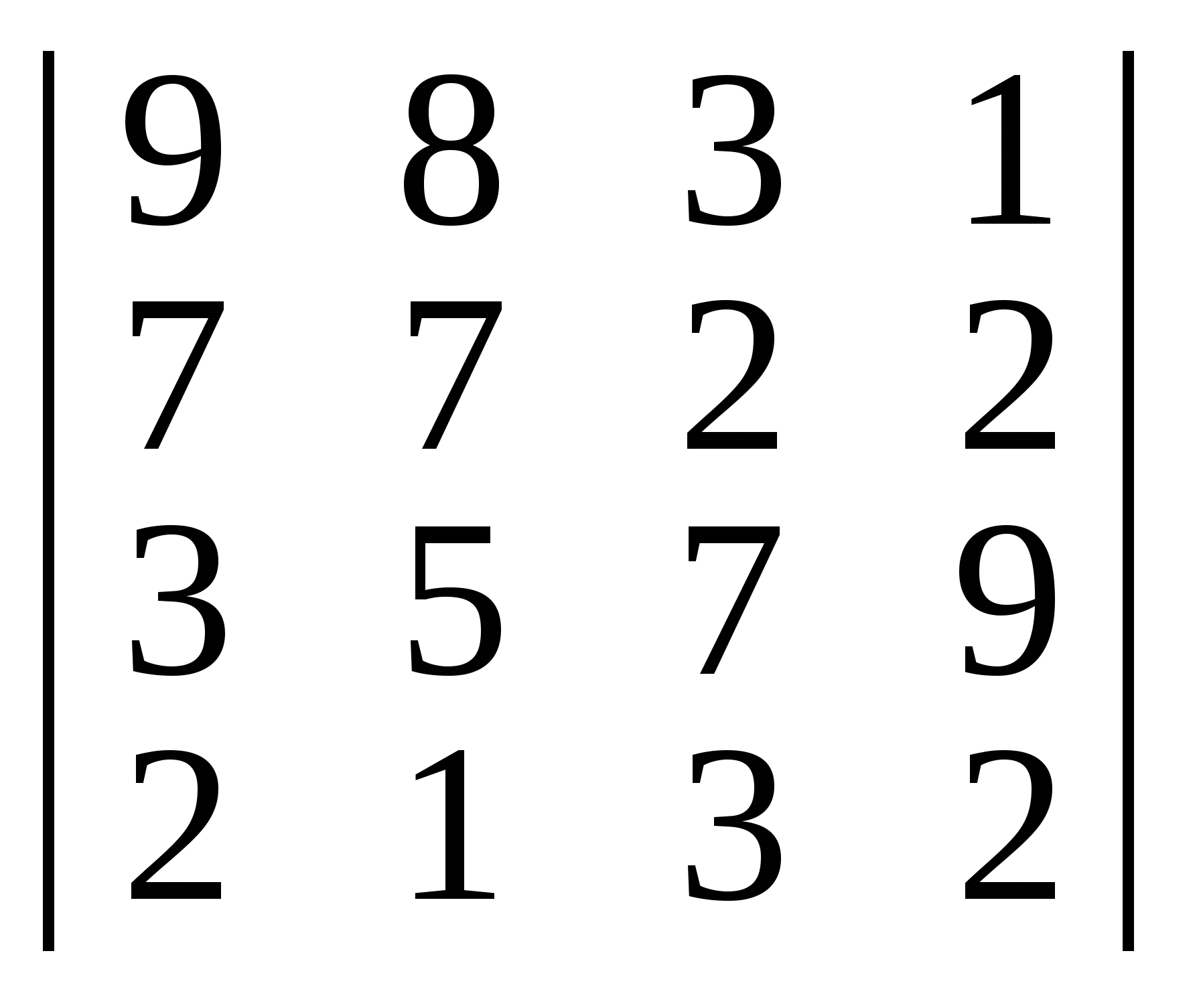 . .
Скільки таких мінорів?
Тема 1.2
Елементи теорії матриць
1.2.1. Основні поняття
Розглянемо ще один математичний об’єкт, пов’язаний із системою рівнянь (1.1).
Означення. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпців. Якщо повернутися до системи рівнянь (1.1), то коефіцієнти при невідомих у лівій частині якраз і утворюють таку прямокутну таблицю:
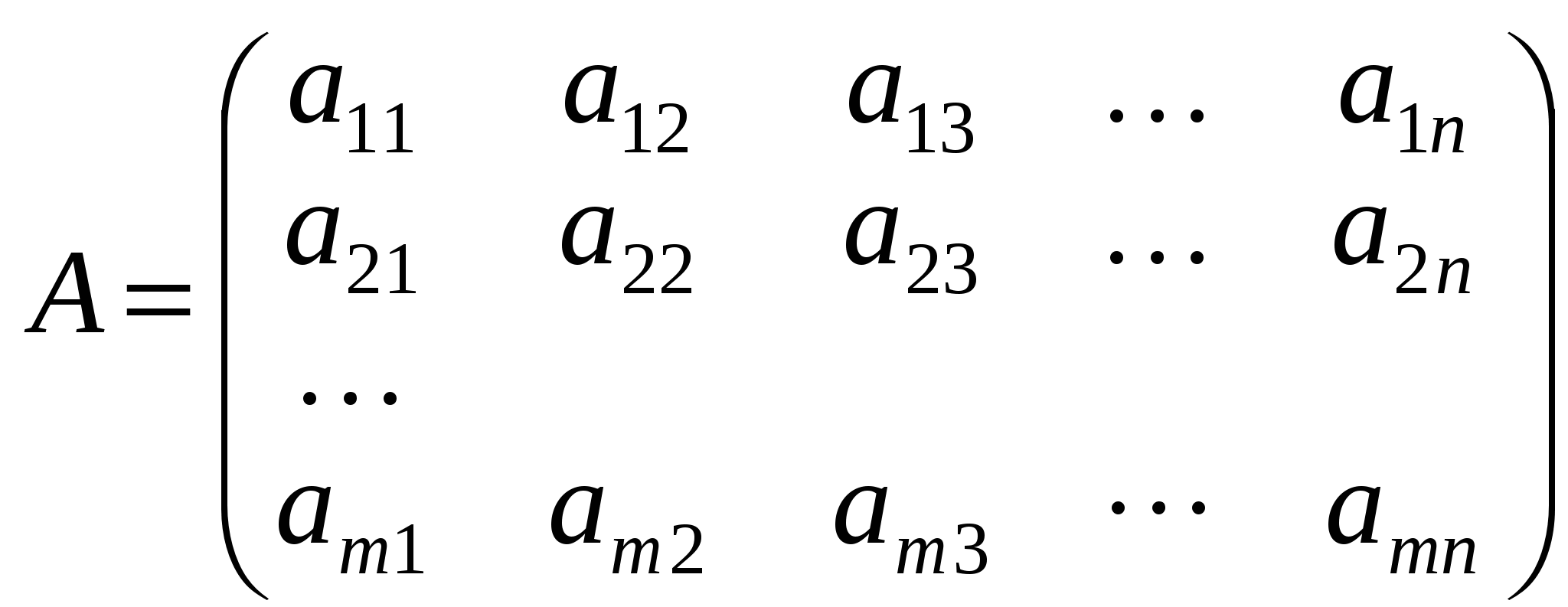 . .
Числа  називаються елементами матриці, а запис називаються елементами матриці, а запис 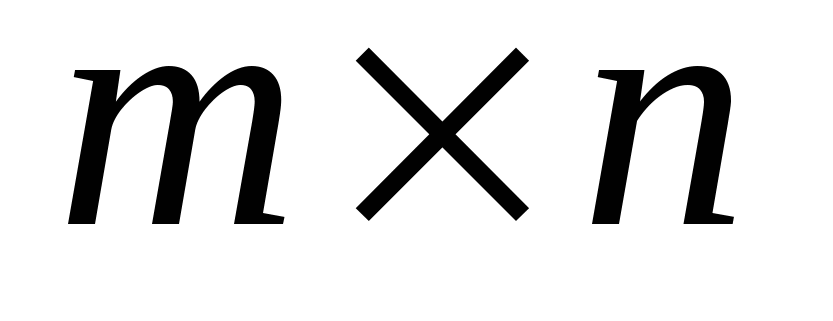 означає її розмір. Зауважимо, що на першому місці в цьому запису зазначено кількість рядків матриці, а на другому — кількість стовпців. Наприклад, запис розміру матриці означає її розмір. Зауважимо, що на першому місці в цьому запису зазначено кількість рядків матриці, а на другому — кількість стовпців. Наприклад, запис розміру матриці 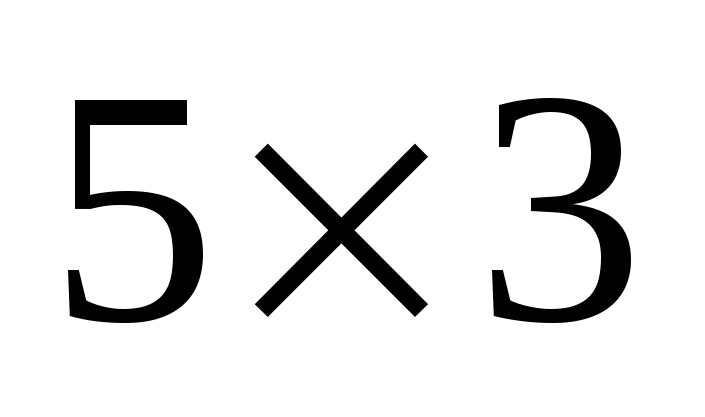 означає, що в ній п’ять рядків і три стовпці. Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною. означає, що в ній п’ять рядків і три стовпці. Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною.
Дві матриці рівні між собою, якщо вони мають однаковий розмір і всі їх відповідні елементи рівні між собою.
Елементи з двома однаковими індексами a11, a22, a33, ... annутворюють головну діагональ матриці. Якщо 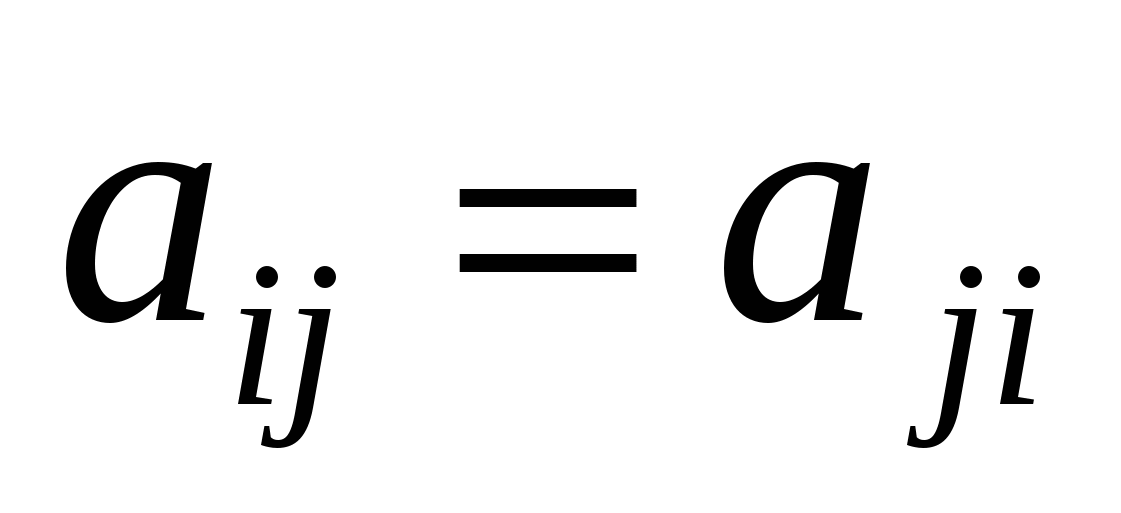 , то матриця називається симетричною. , то матриця називається симетричною.
Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю, називається одиничною матрицею:
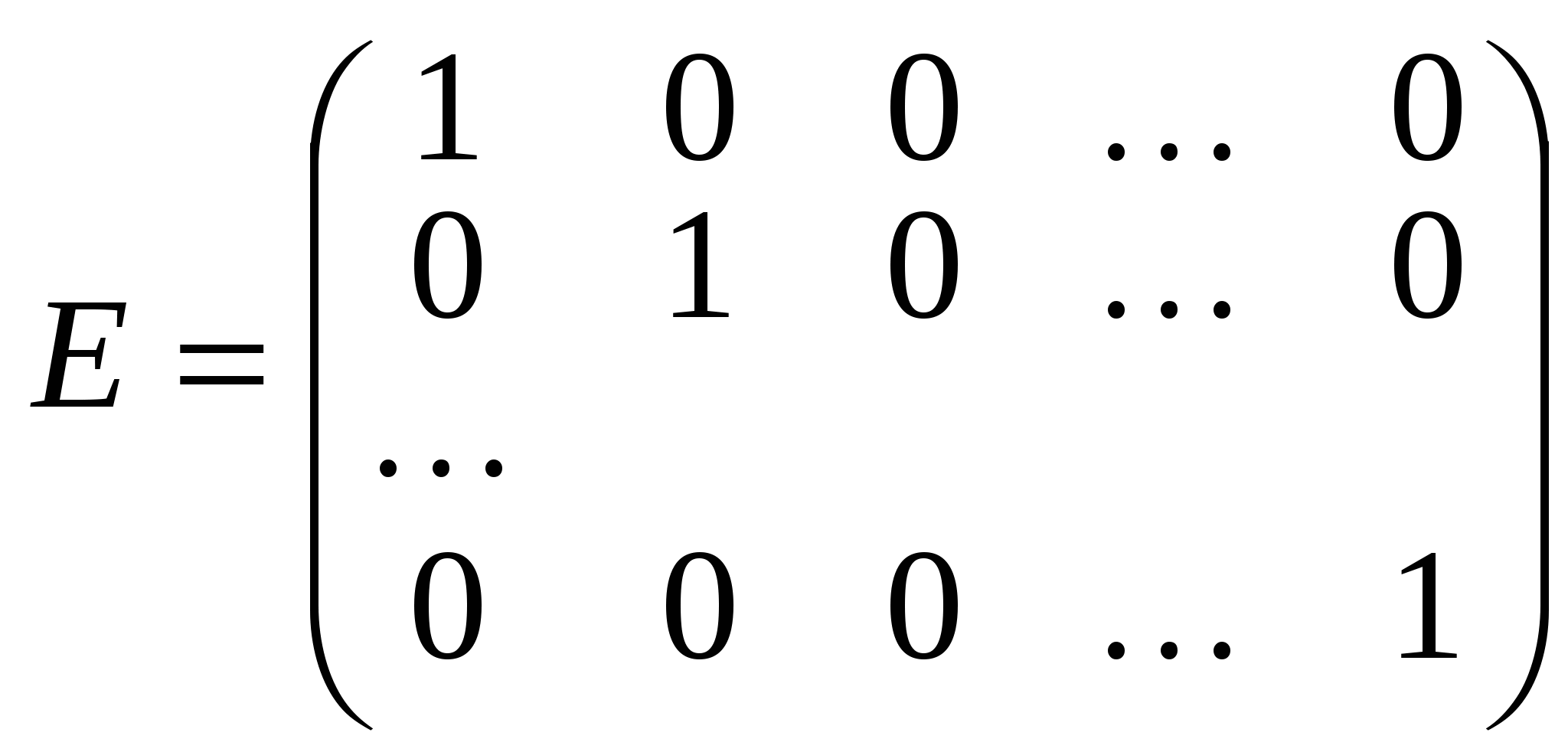 . .
Коли всі елементи матриці, що містяться по один бік від головної діагоналі, дорівнюють нулю, то матриця називається трикутною.
Кожній квадратній матриці можна поставити у відповідність визначник, який складається з тих самих елементів.
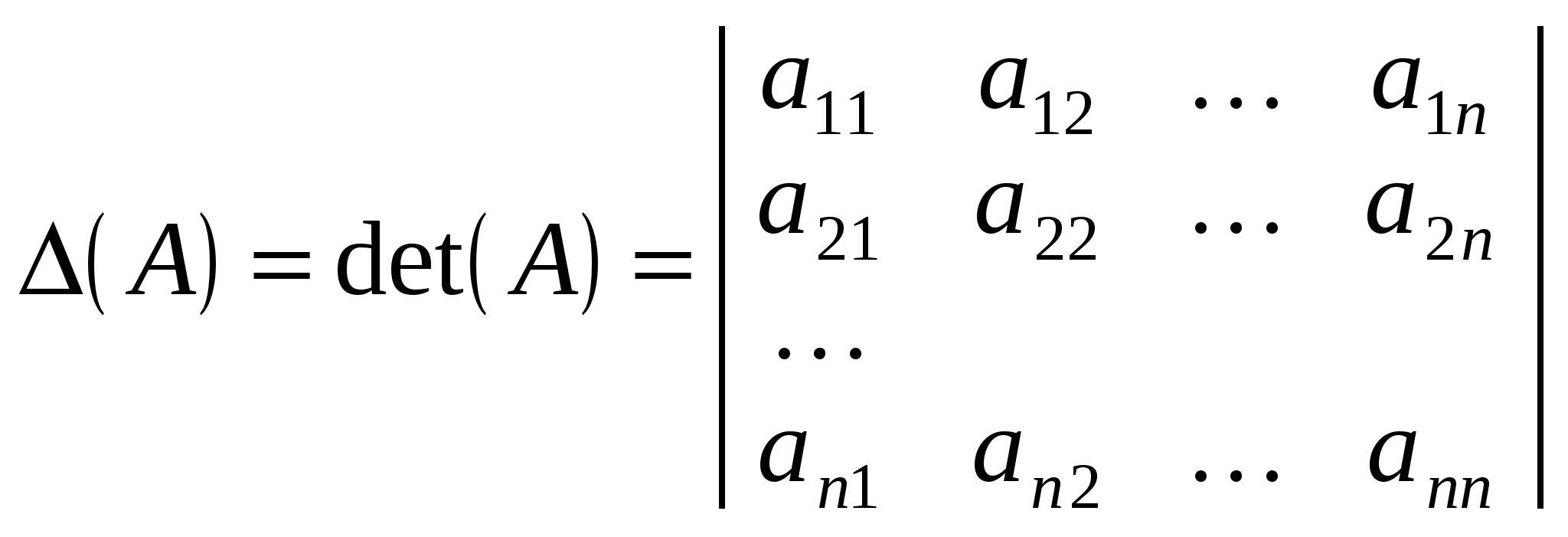 . .
Якщо такий визначник відмінний від нуля, то матриця називається неособливою, або невиродженою. Якщо визначник дорівнює нулю, то матриця особлива, або вироджена.
1.2.2. Дії з матрицями
Сумою матриць одного й того самого порядку 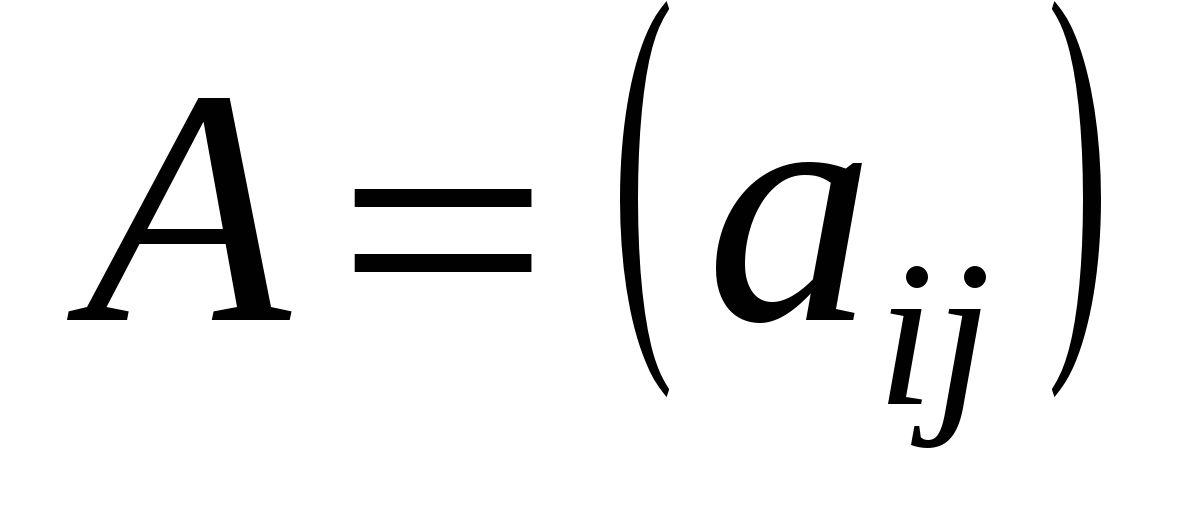 і і 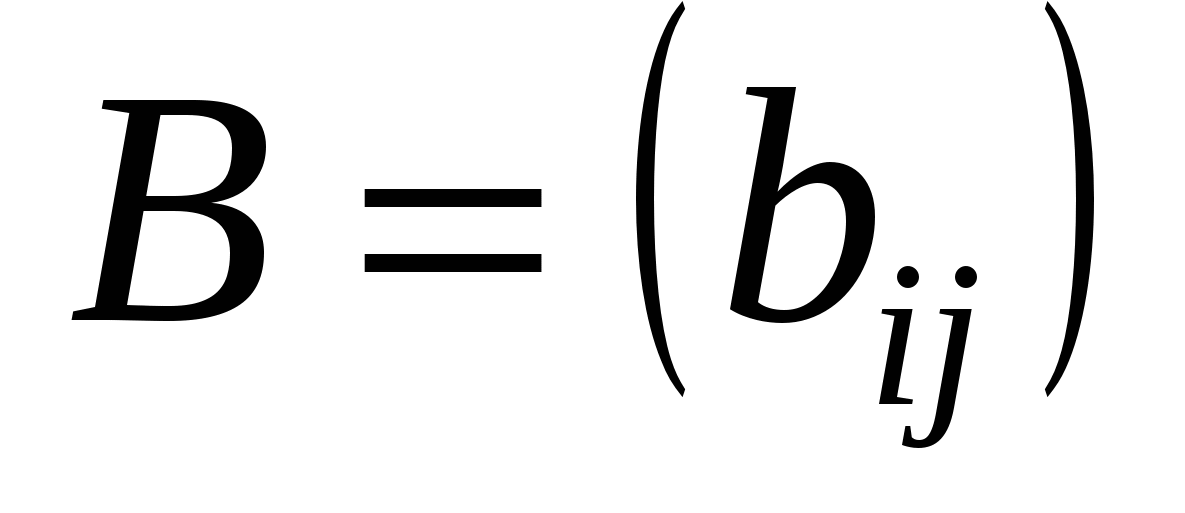 називається матриця називається матриця 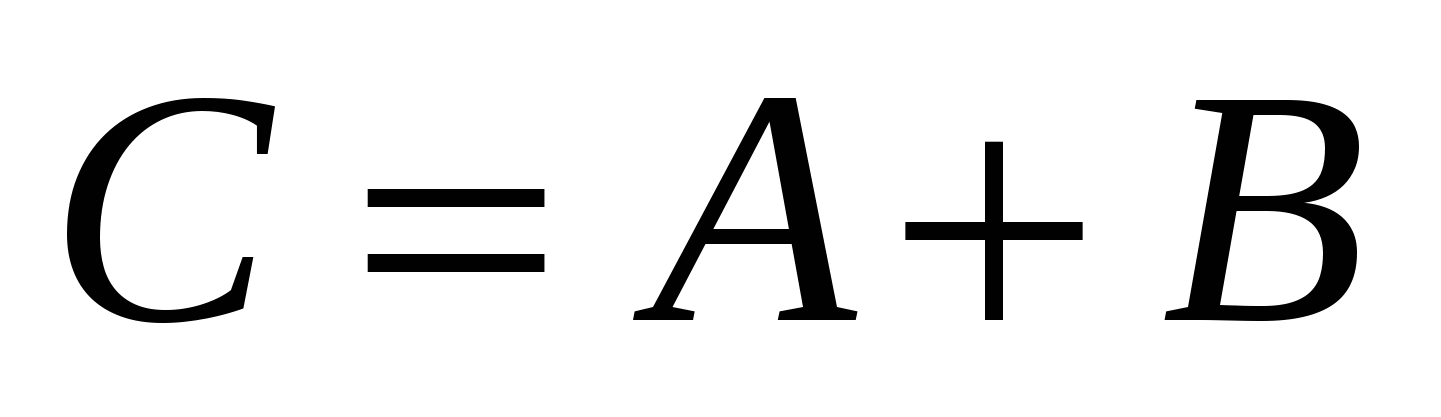 ; ; 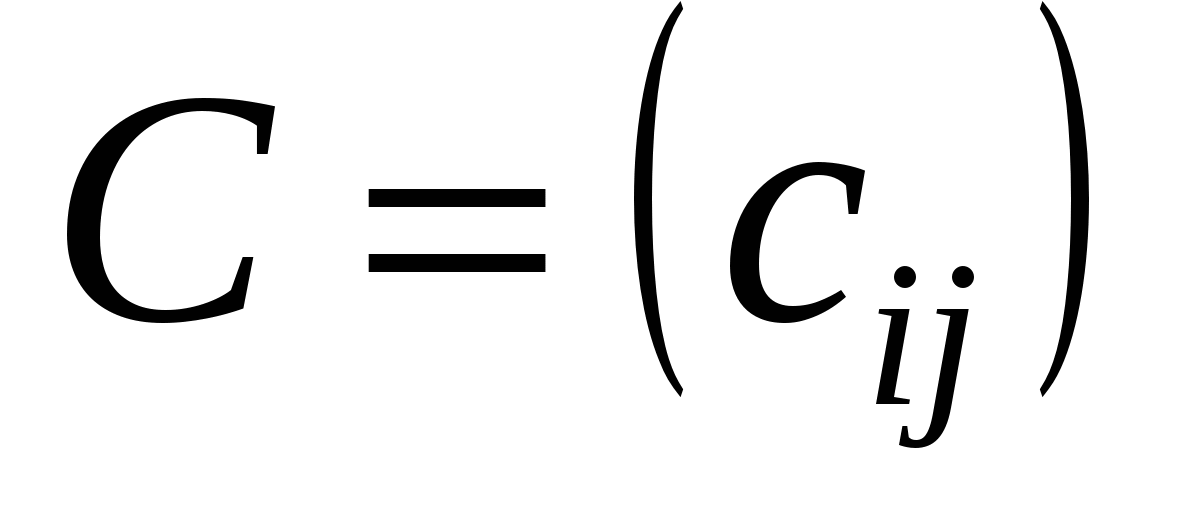 , будь-який , будь-який
елемент якої дорівнює сумі відповідних елементів матриць
А і В: 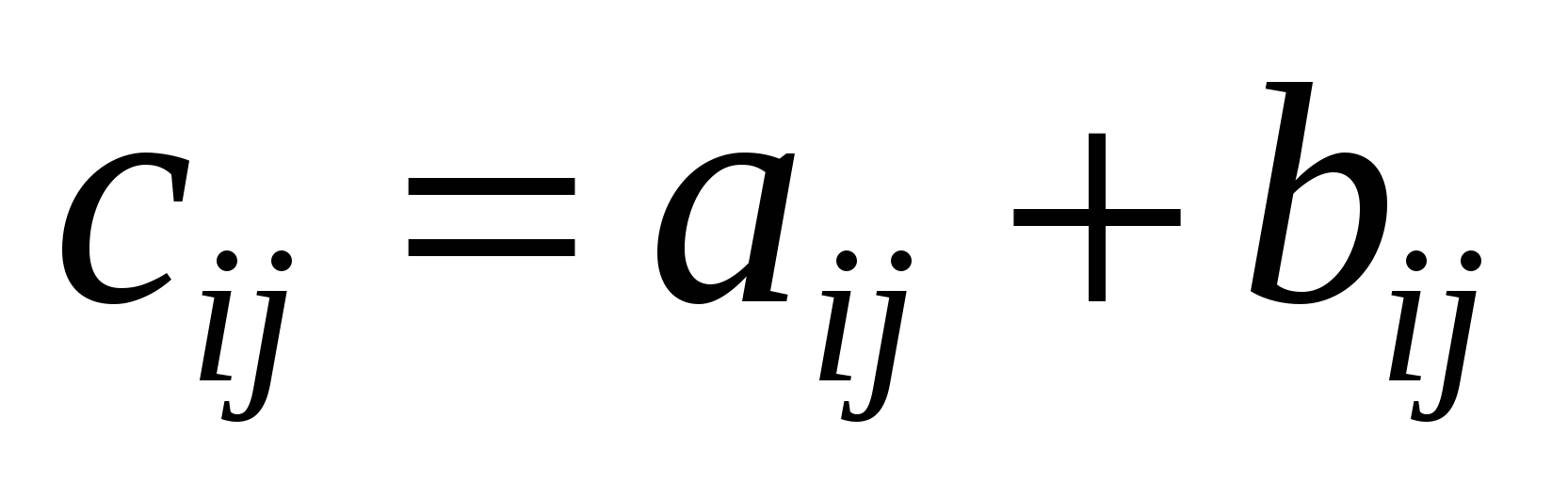 . Наприклад обидві матриці . Наприклад обидві матриці 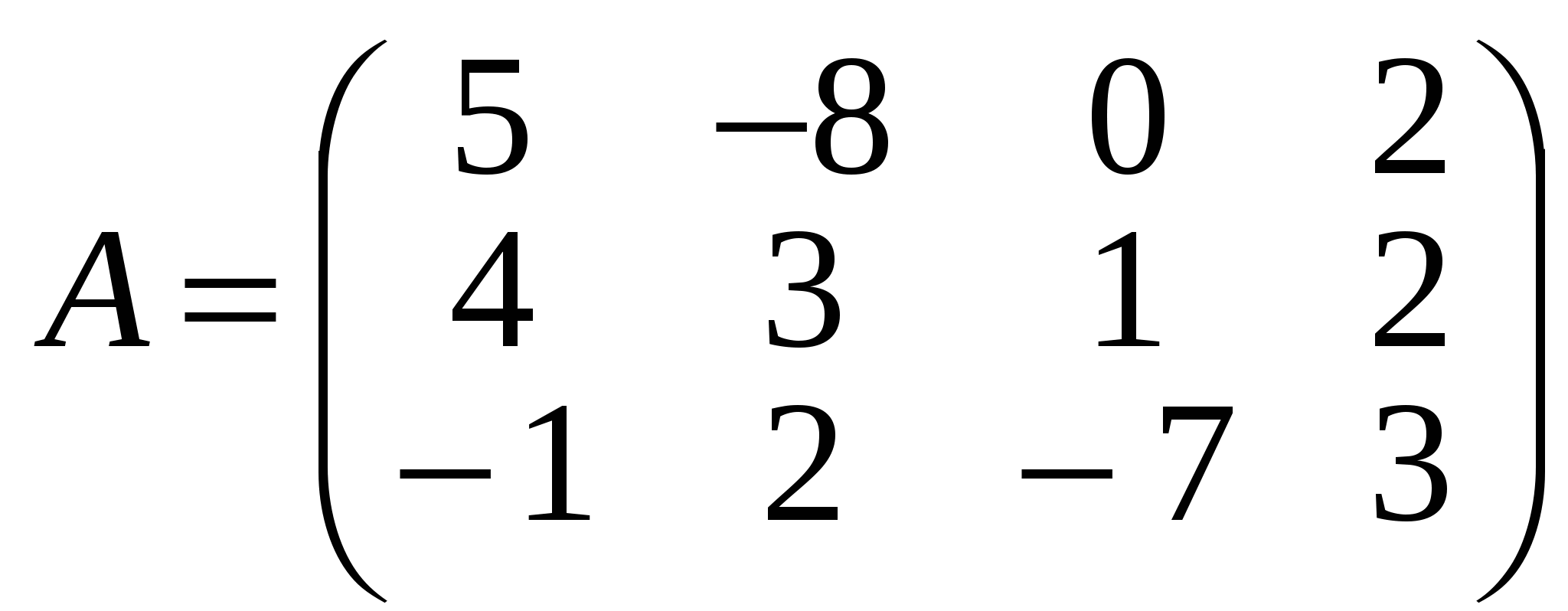 , , 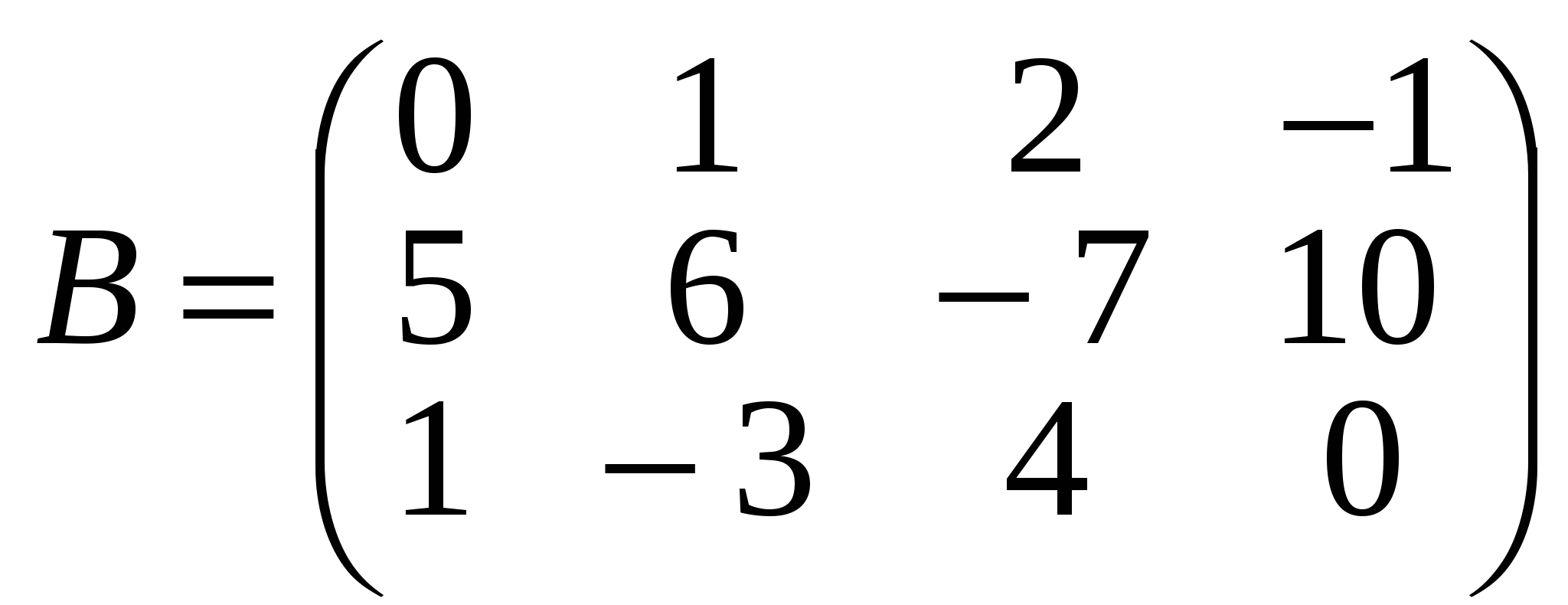 мають розмір мають розмір  , тому за означенням можна утворити їх суму — матрицю , тому за означенням можна утворити їх суму — матрицю
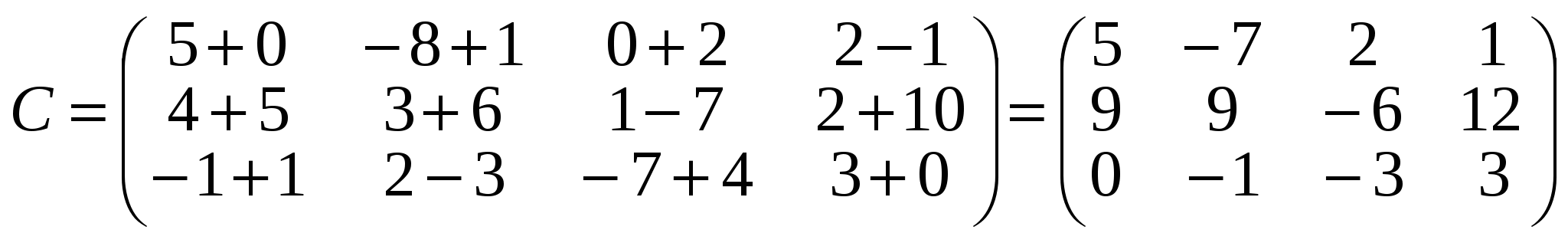 . .
2. Добутком матриці 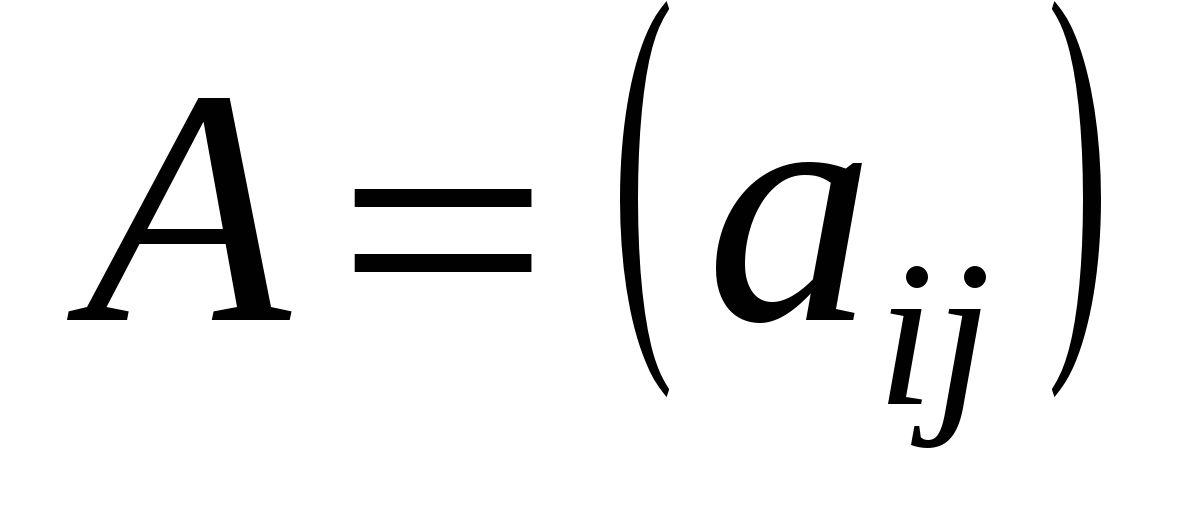 на деяке число на деяке число  називається така матриця С, кожен елемент якої називається така матриця С, кожен елемент якої  утворюється множенням відповідних елементів матриці А на утворюється множенням відповідних елементів матриці А на  , , 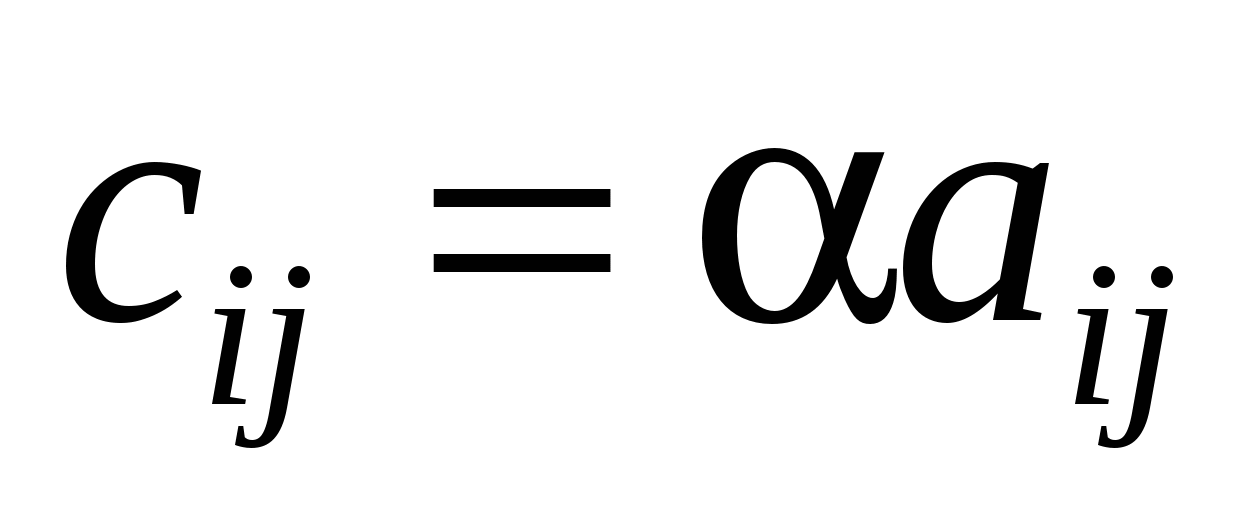 . .
Приклад. 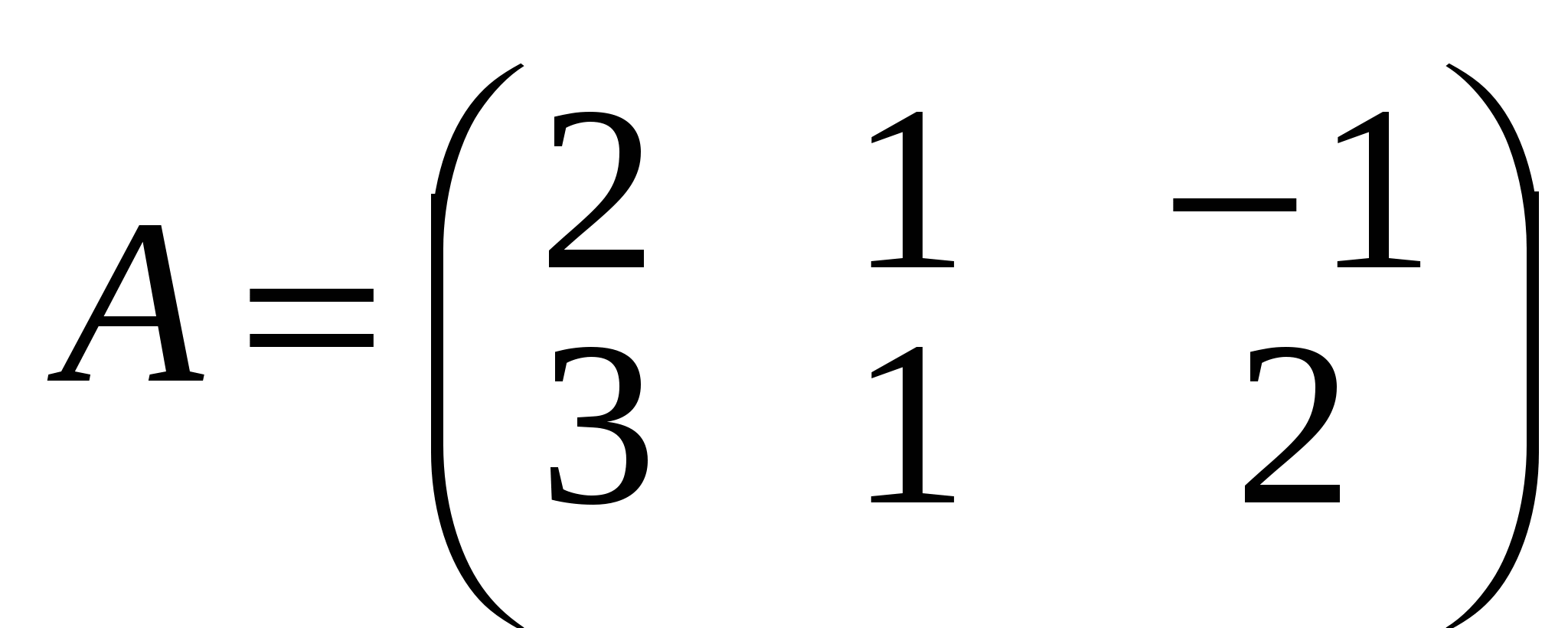 , , 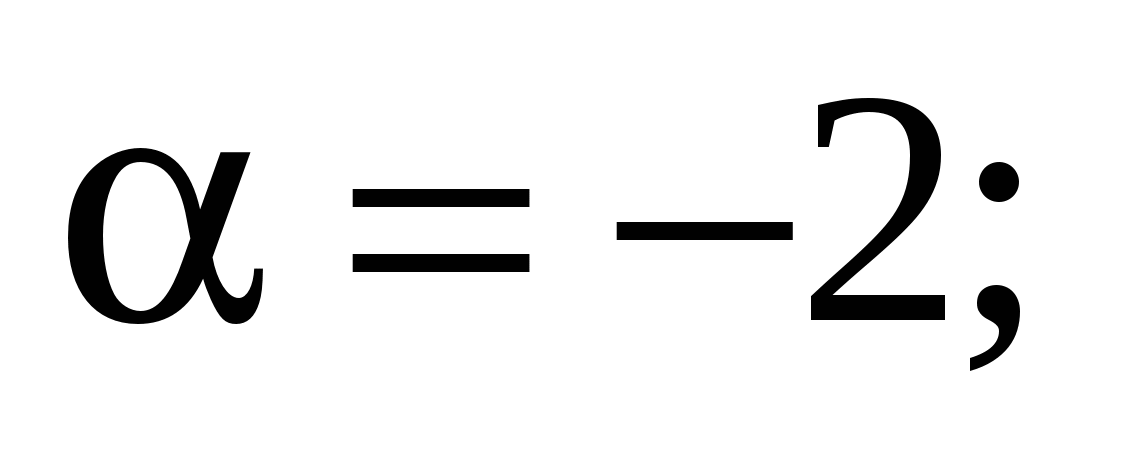 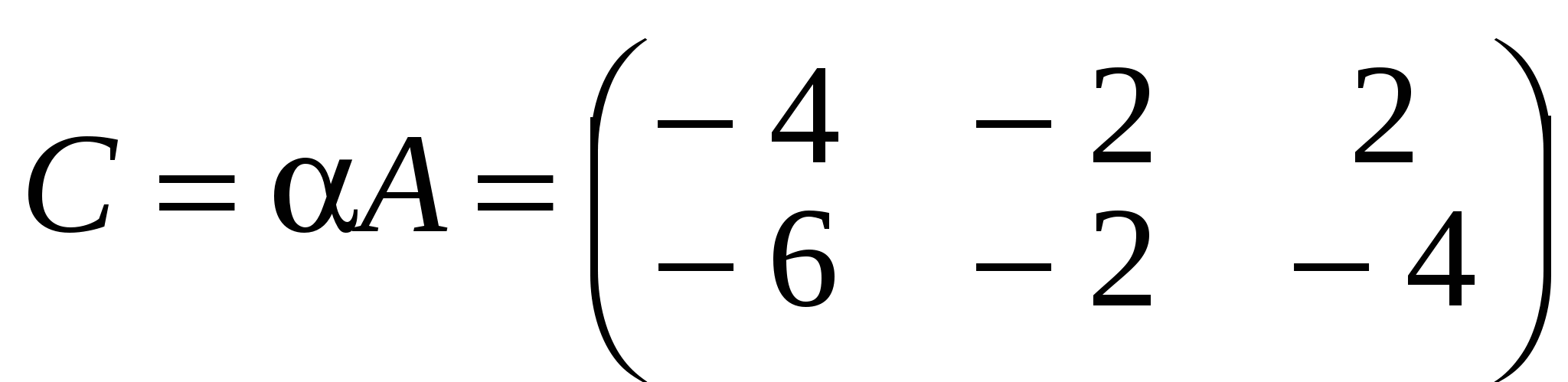 . .
Очевидно, що для суми матриць і добутку матриць на число виконуються рівності:
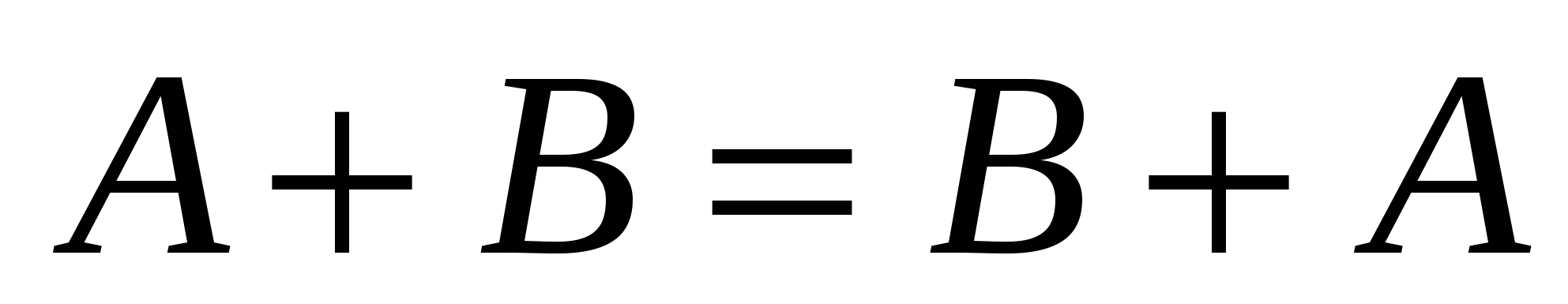 ; 2) ; 2) 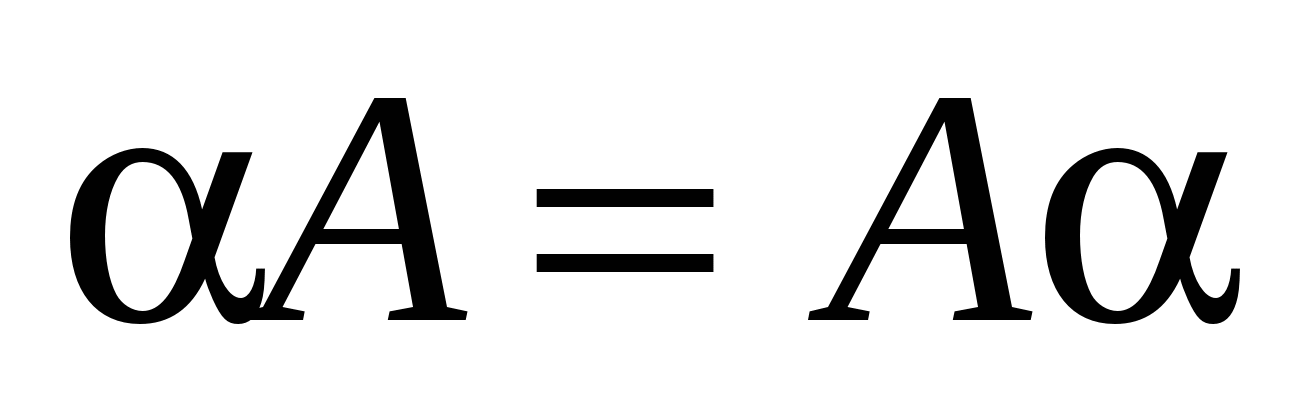 ; 3) ; 3) 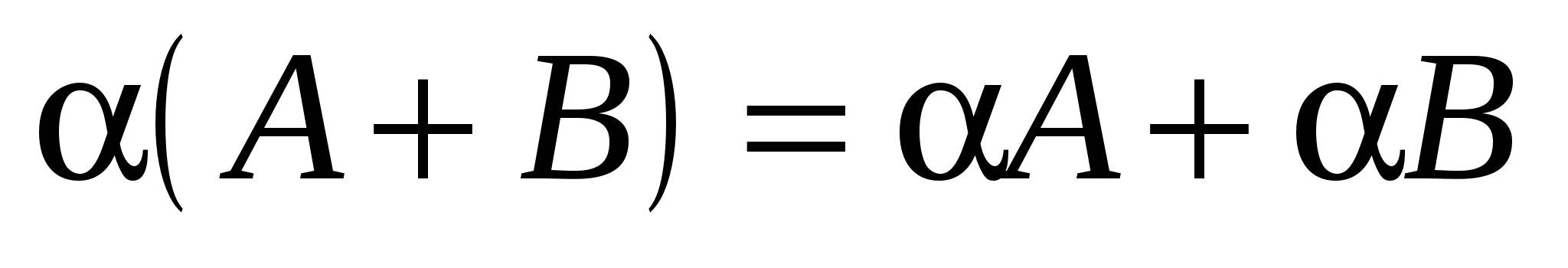 ; 4) ; 4) 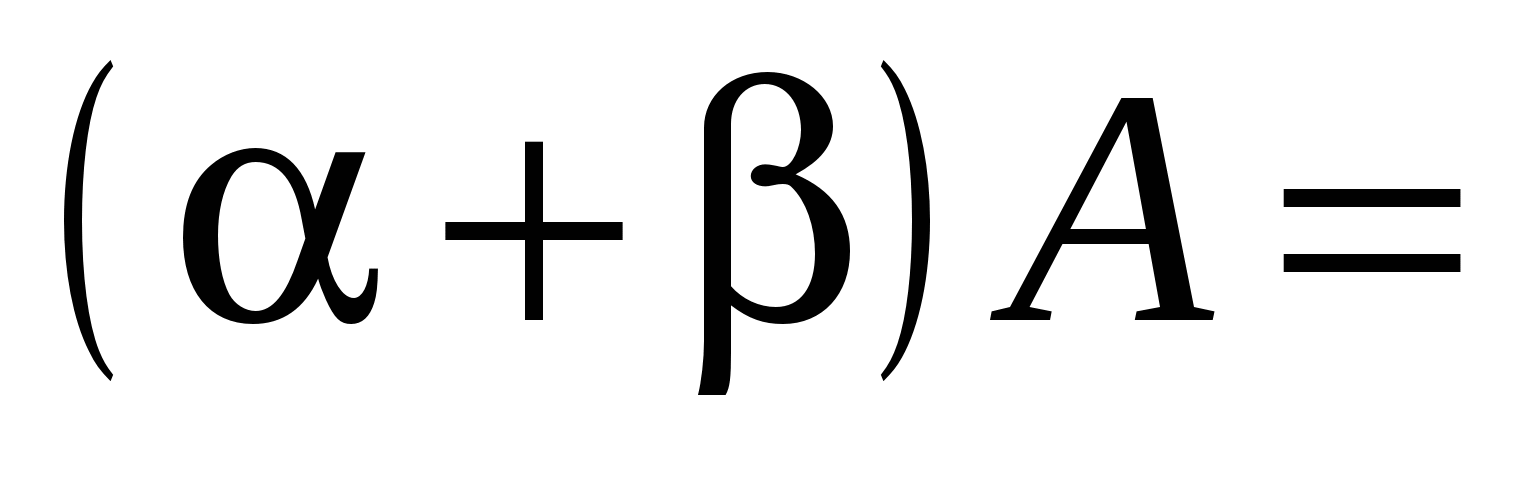 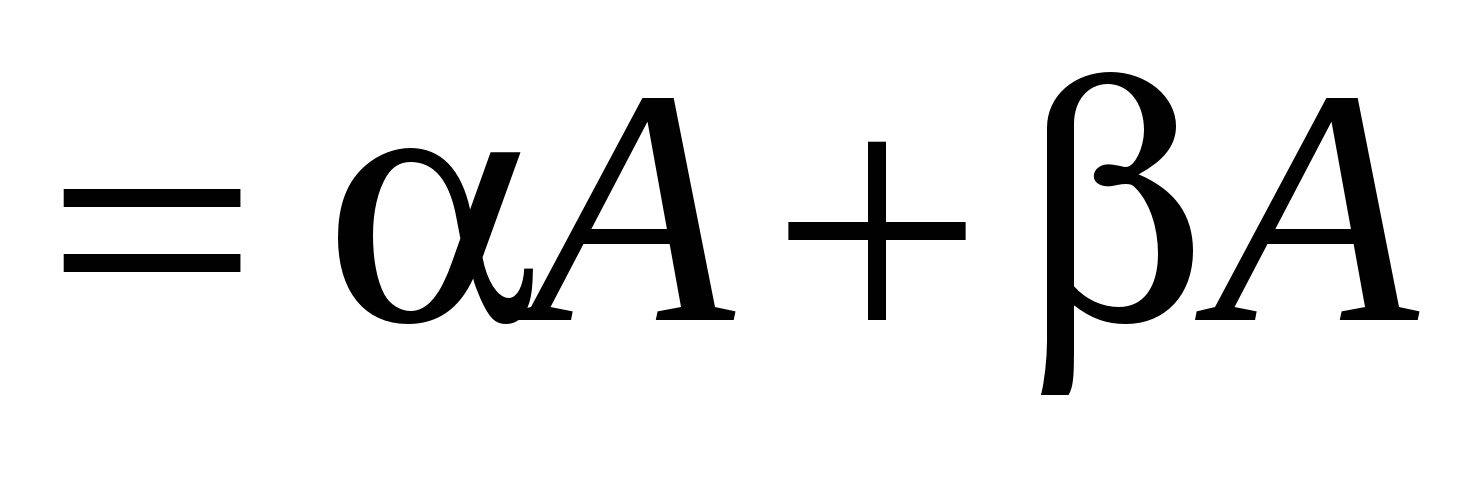 , 5) , 5) 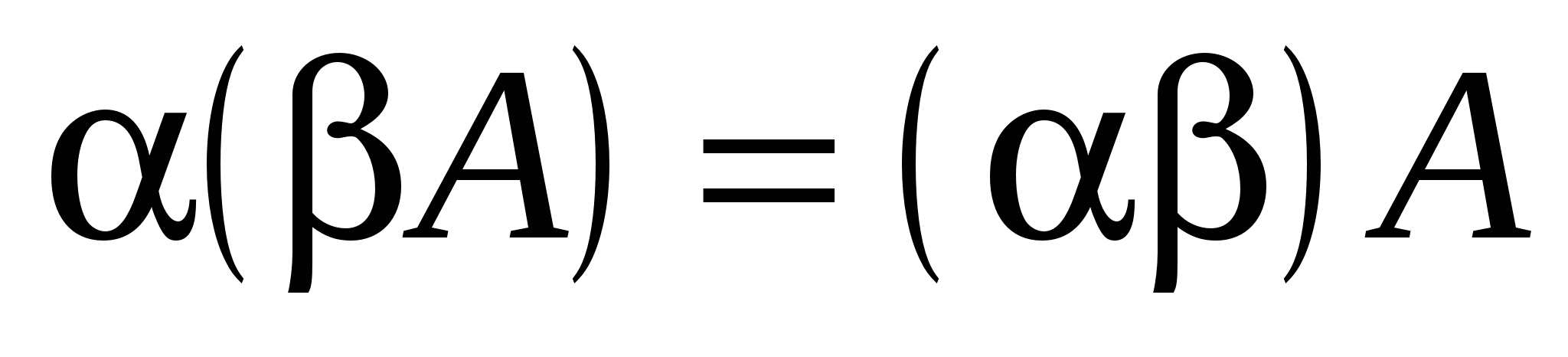 . .
Добутком матриці 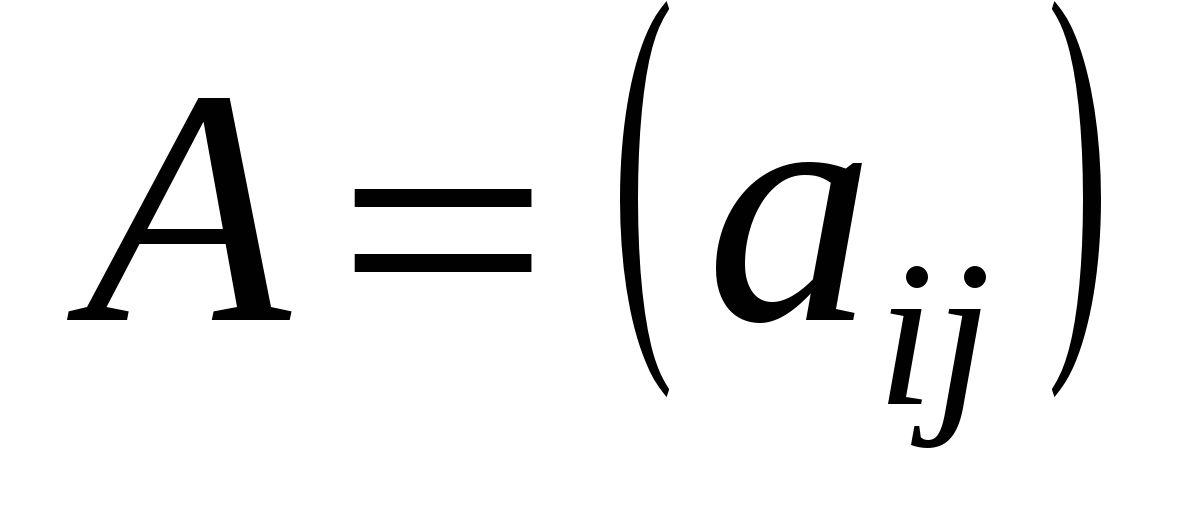 розміру розміру 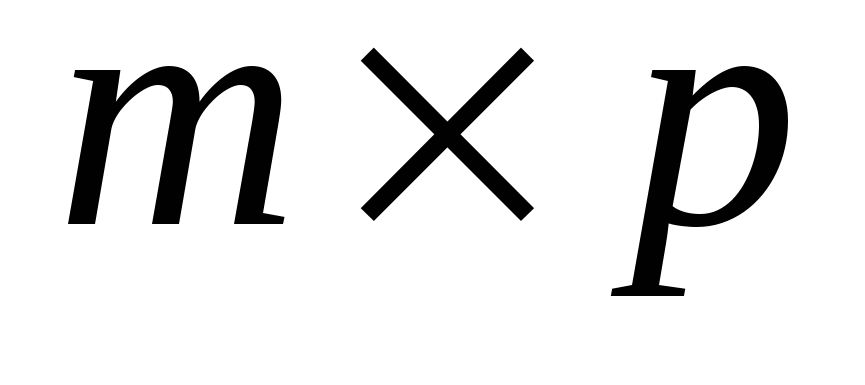 на матрицю на матрицю 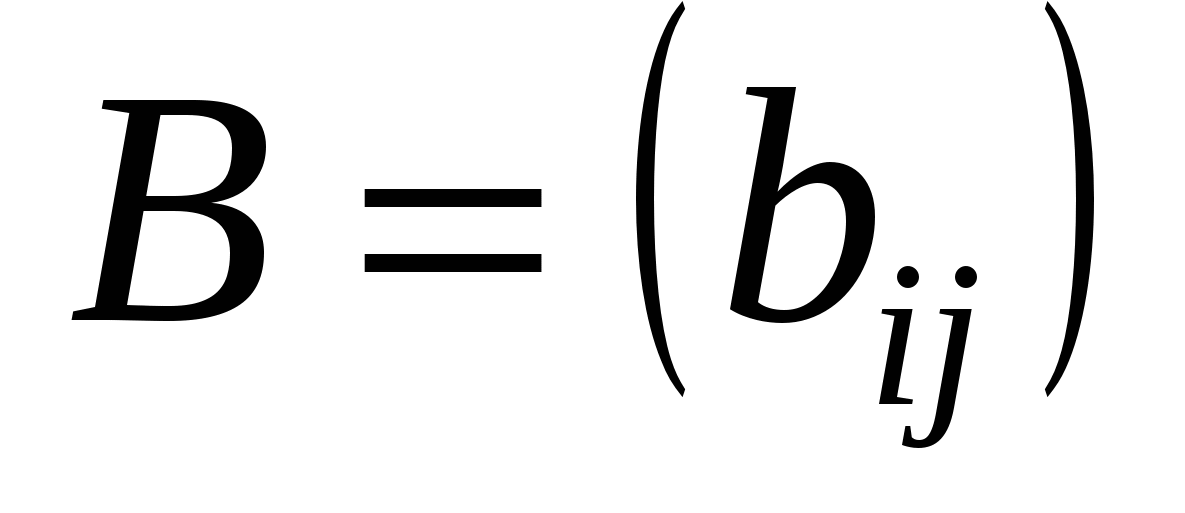 розміру розміру 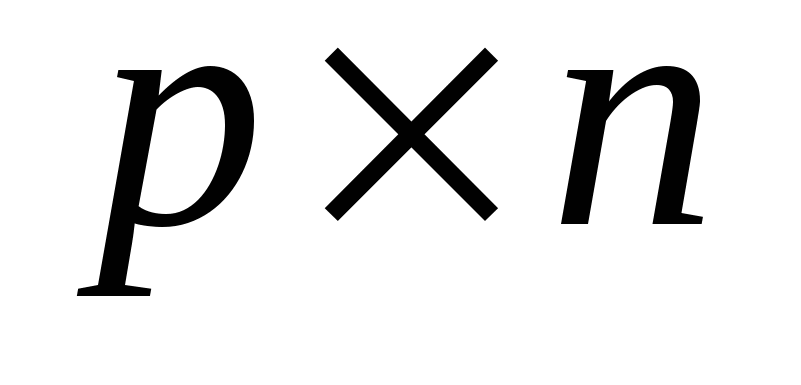 називається така матриця називається така матриця 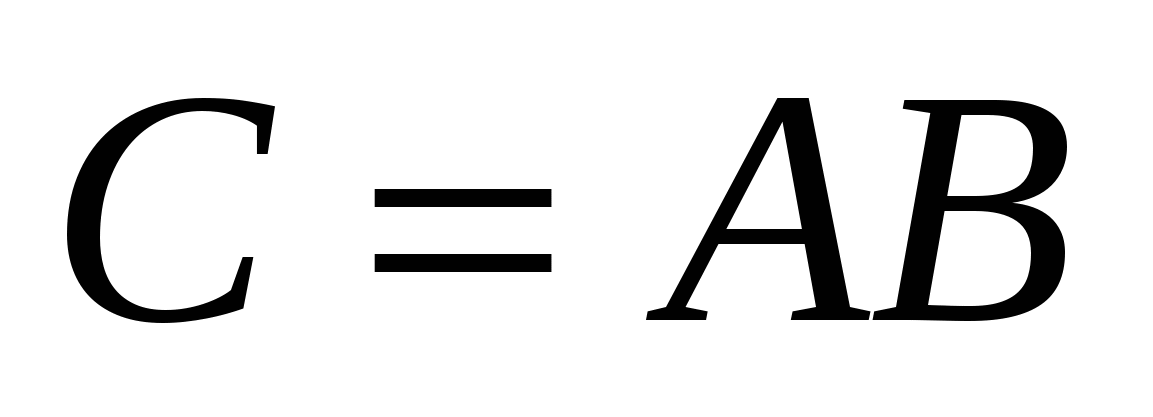 розміру розміру 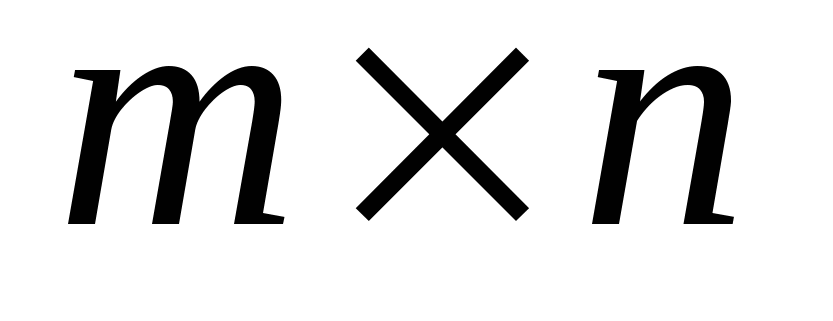 , , 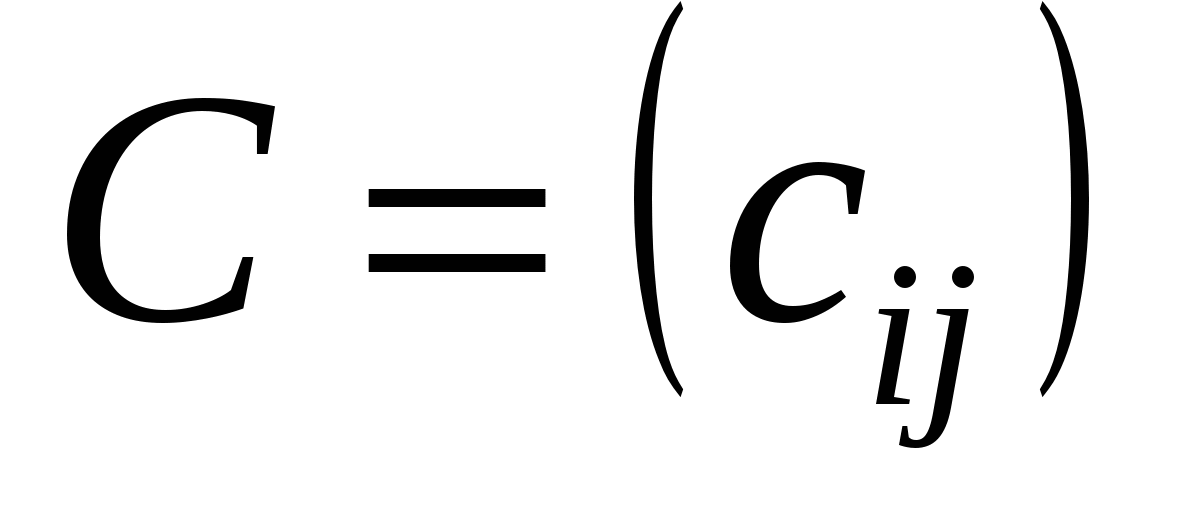 , кожний елемент можна знайти за формулою: , кожний елемент можна знайти за формулою:
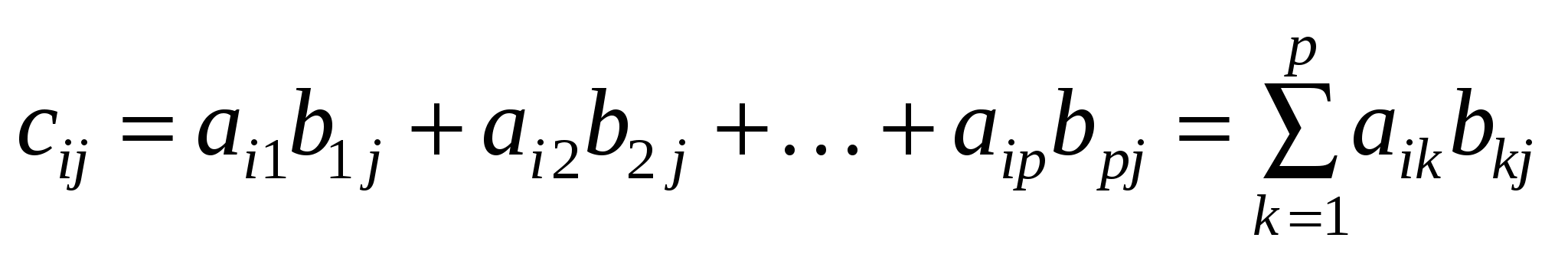 . .
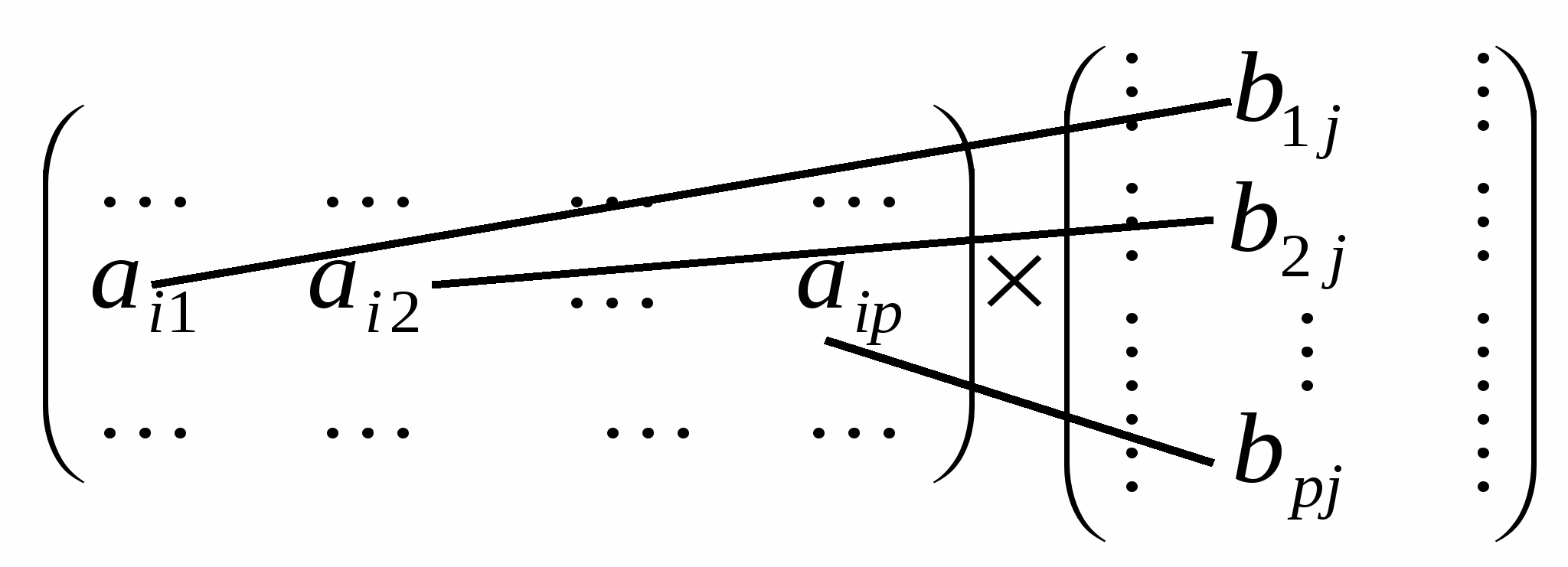
Кожний елемент матриці С утворюється як сума добутків відповідних елементів і-го рядка матриці А на відповідні елементи
j-го стовпця матриці В, тобто за схемою:
Зазначимо, що в результаті множення дістанемо матрицю розміру 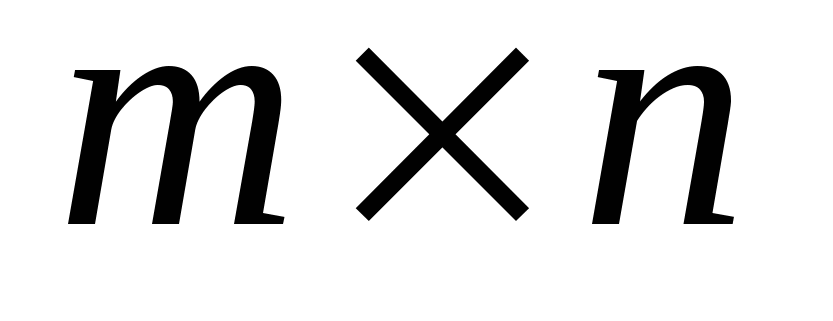 . .
З означення випливає, що добуток матриць некомутативний: 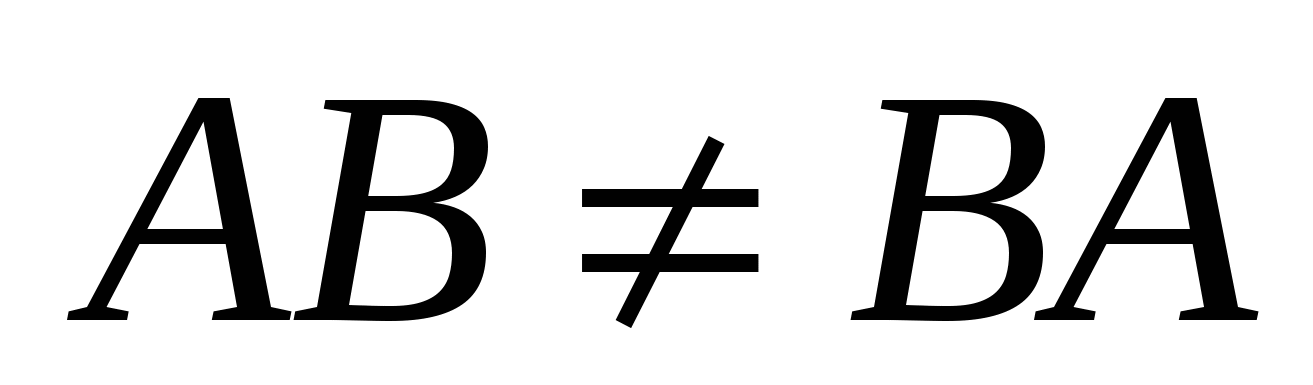 . .
Повернемось до системи рівнянь (1.1) і утворимо матриці: А — коефіцієнтів при невідомих, Х — невідомих, В — вільних членів:
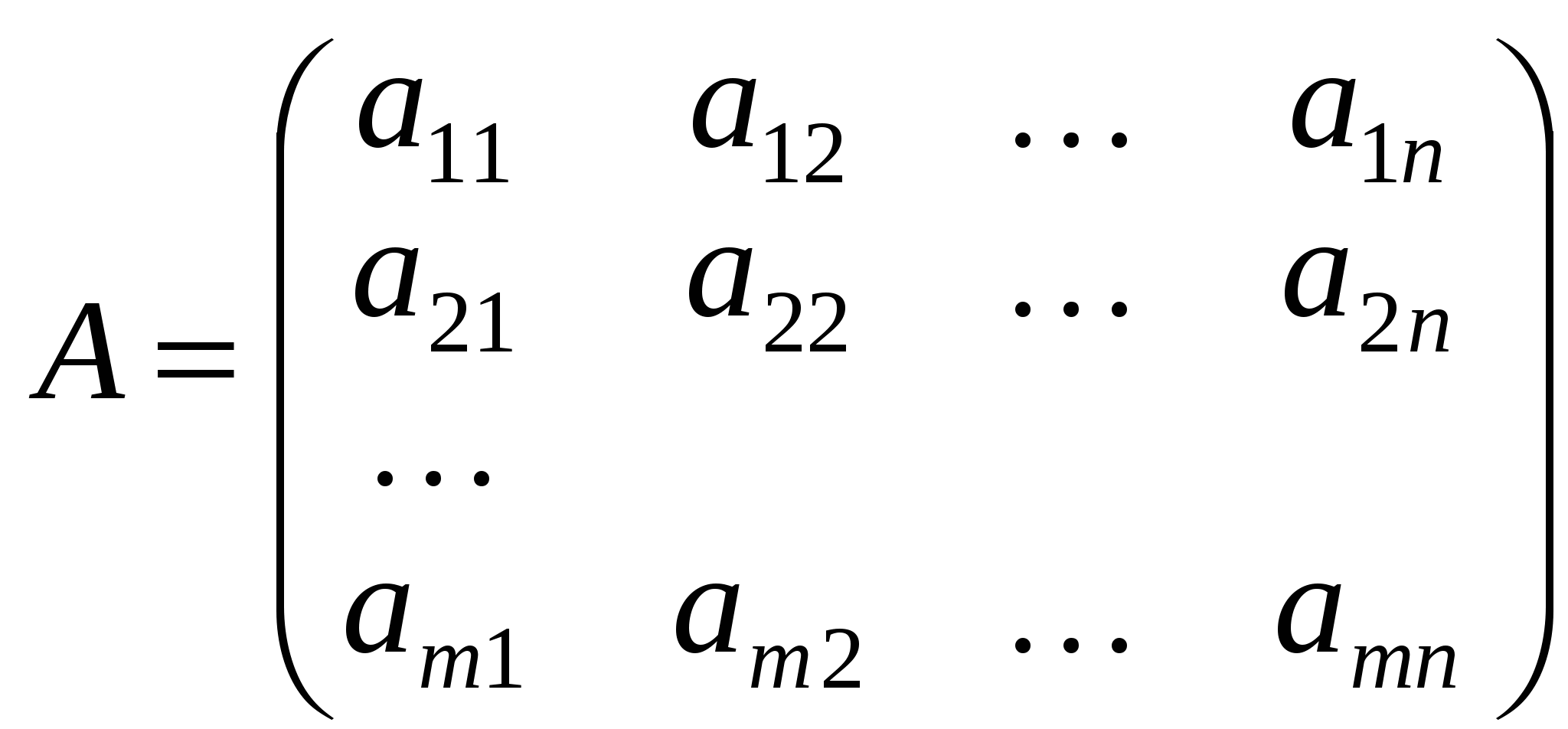 , , 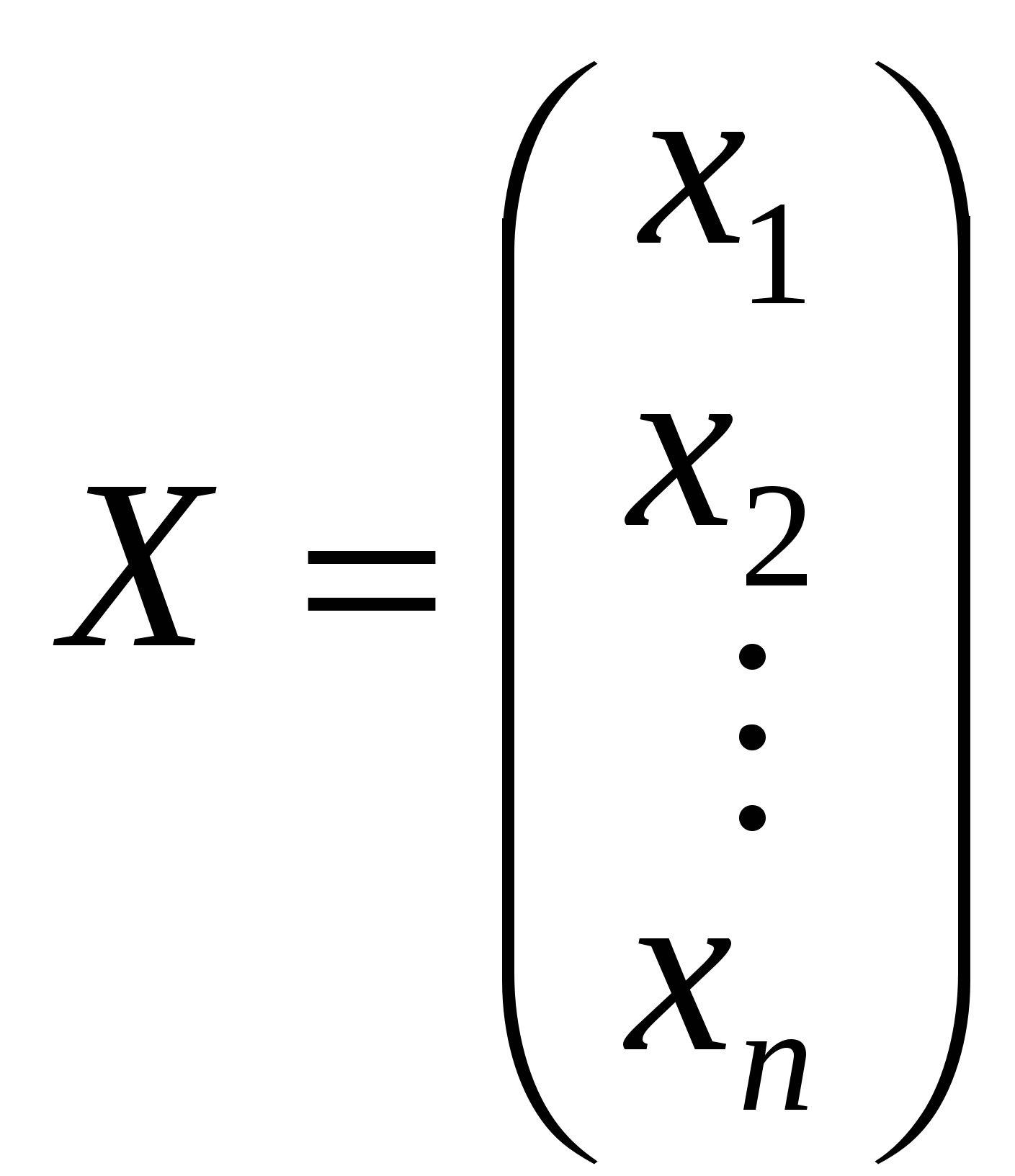 , , 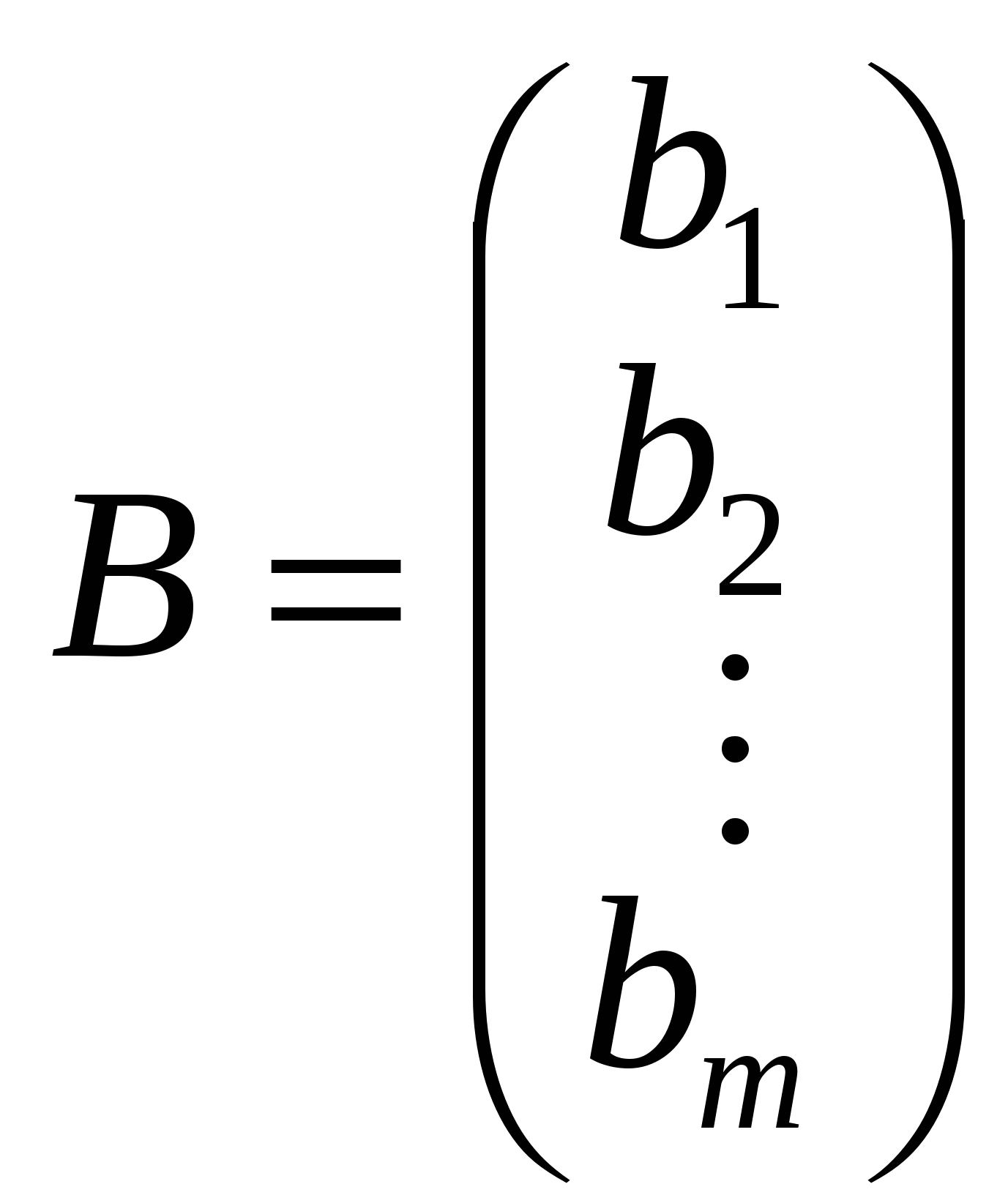 . .
Тоді згідно з означенням добутку матриць систему рівнянь (1.1) можна записати в матричному вигляді:
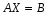 , (1.5) , (1.5)
який значно скорочує запис системи рівнянь.
1.2.3. Обернена матриця
Означення.Матриця А–1 називається оберненою матрицею до квадратної невиродженої матриці А, якщо виконується співвідношення: 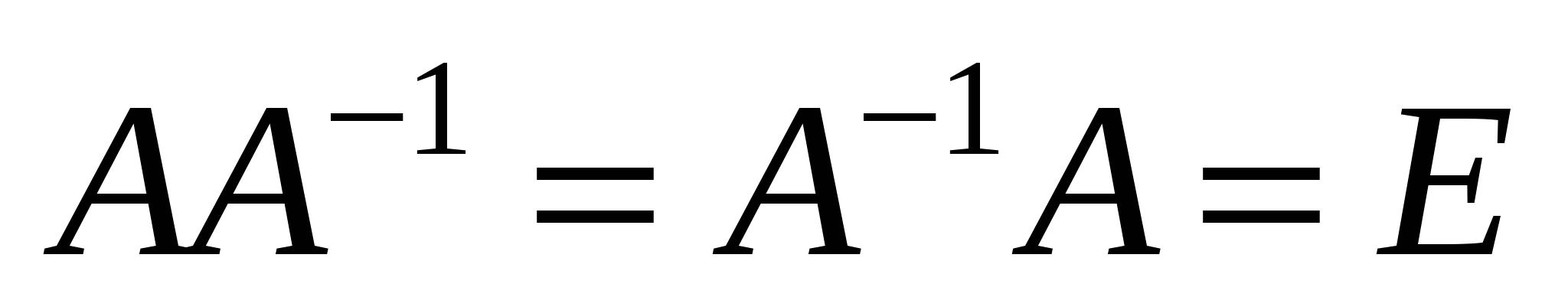 . .
Нехай дано квадратну матрицю А. Доведемо, що коли 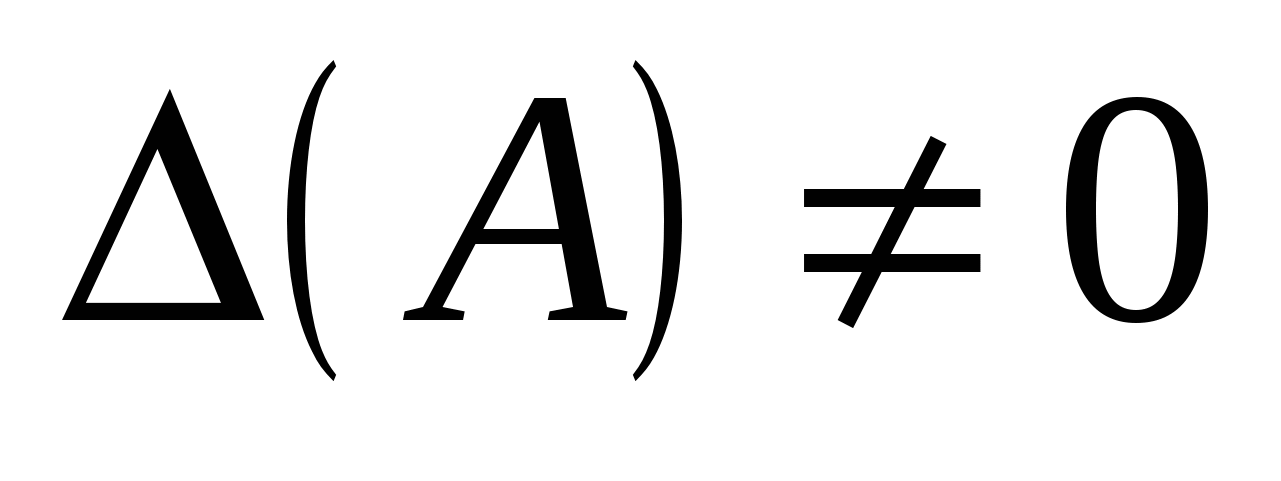 , існує обернена матриця А–1. Розглянемо матрицю: , існує обернена матриця А–1. Розглянемо матрицю:
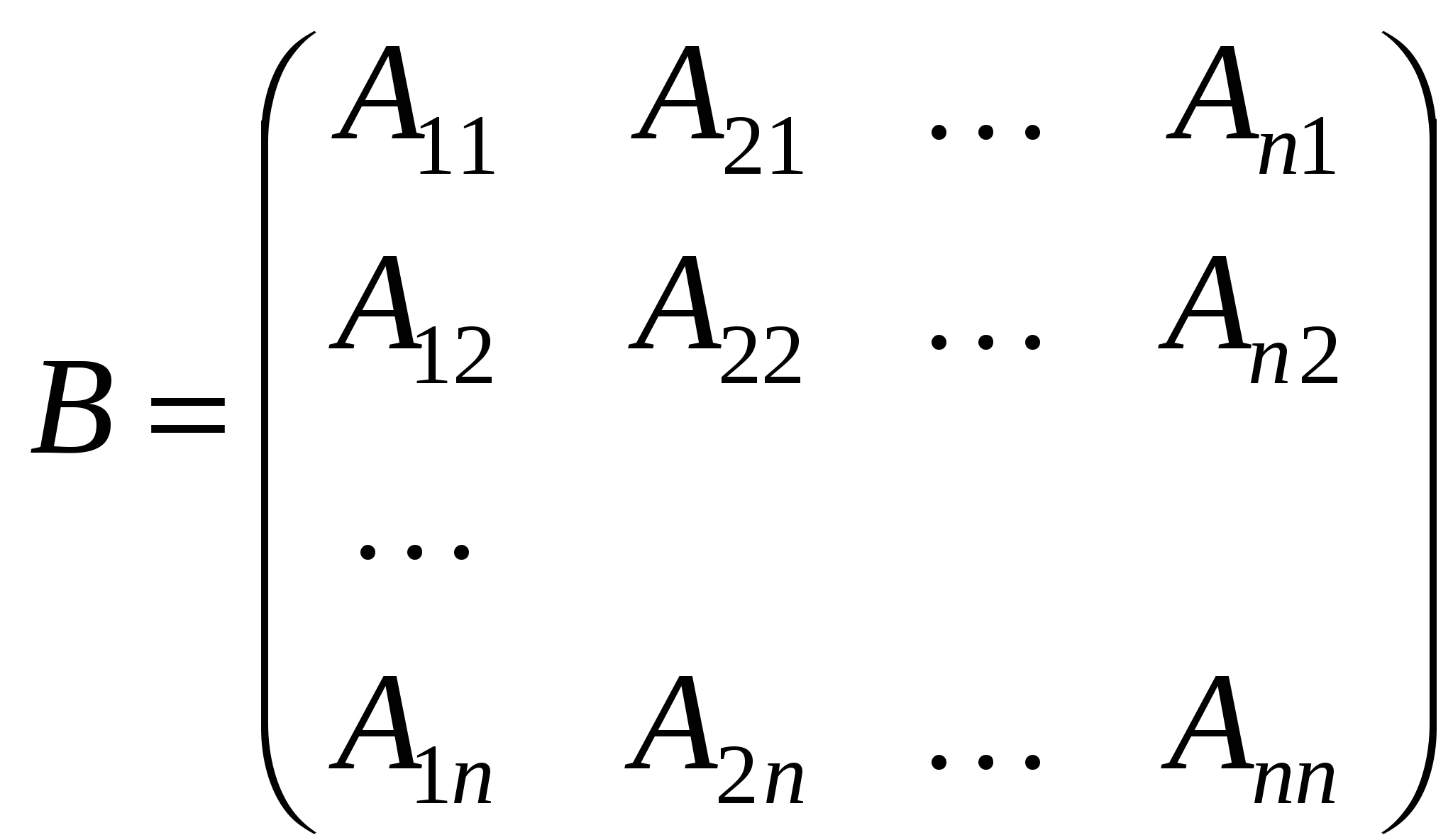 . Утворимо добутки . Утворимо добутки 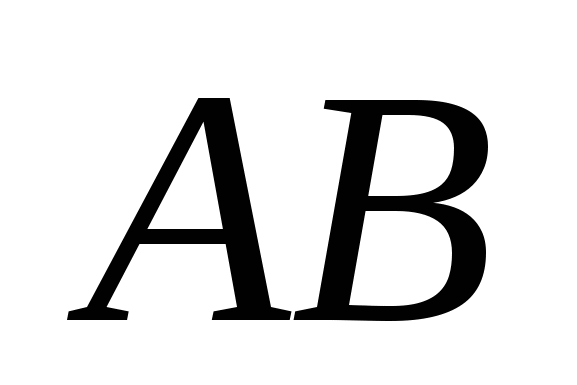 і і 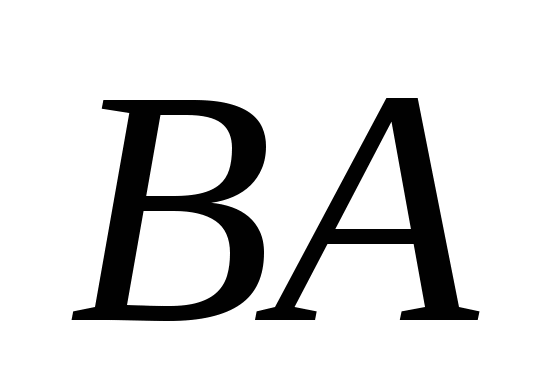 . .
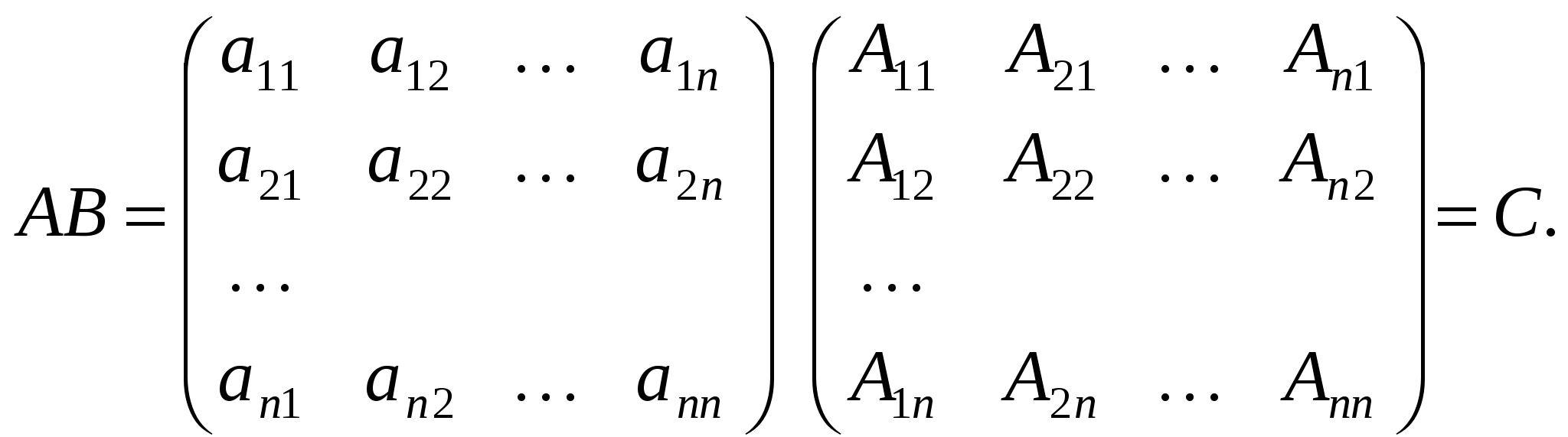
За правилом множення матриць елементи матриці С знаходимо за формулою:
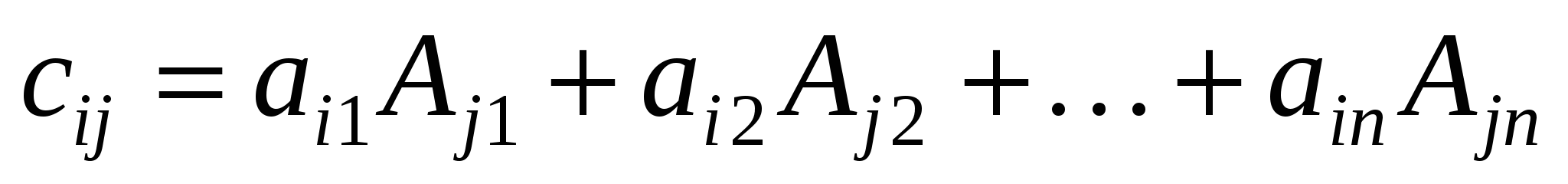 . (1.6) . (1.6)
Якщо i = j, то згідно з формулою (1.3) маємо: 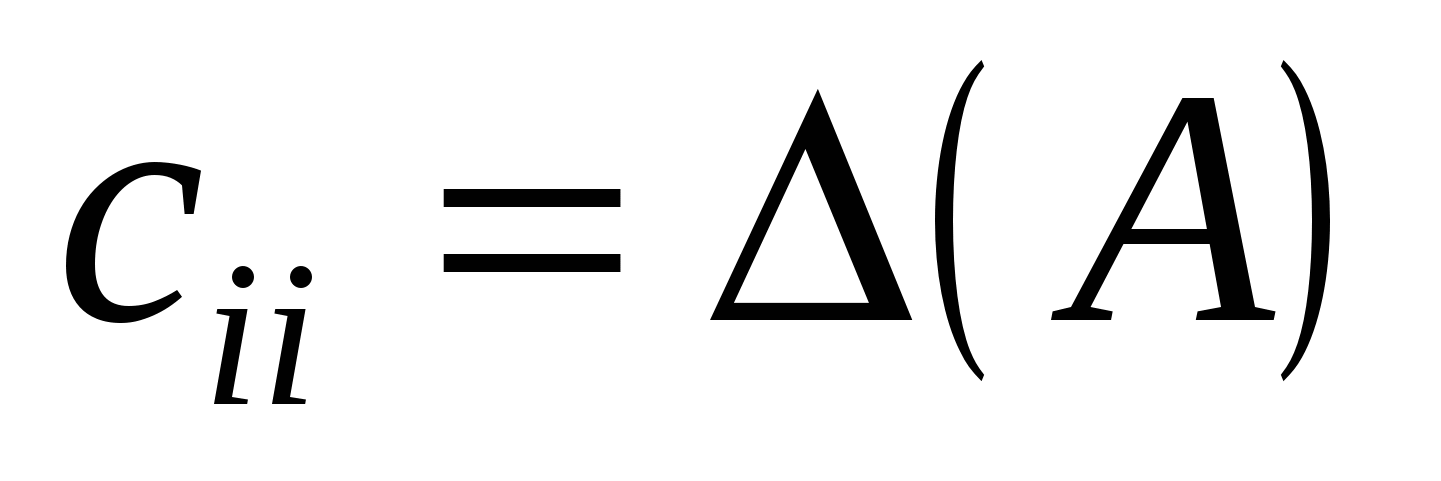 , тобто знаходимо значення визначника матриці А; якщо , тобто знаходимо значення визначника матриці А; якщо 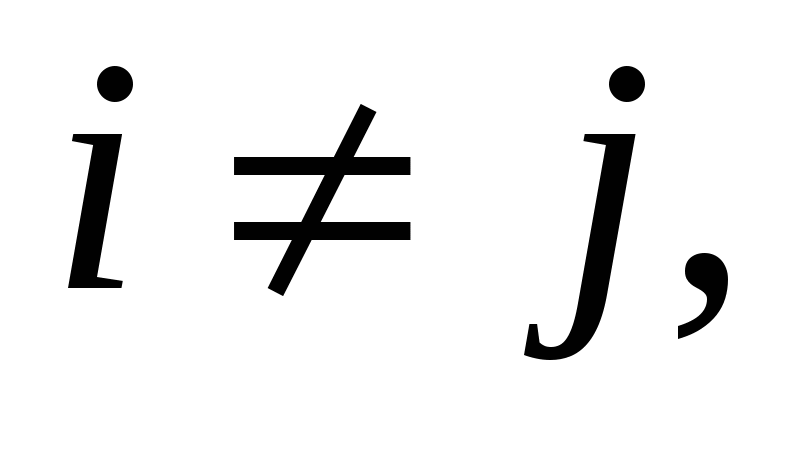 то вираз (1.6) є сумою добутків елементів i-го рядка визначника на алгебраїчні доповнення, що відповідають j-му рядку цього самого визначника. За властивістю 9 визначників така алгебраїчна сума дорівнює нулю. Отже, то вираз (1.6) є сумою добутків елементів i-го рядка визначника на алгебраїчні доповнення, що відповідають j-му рядку цього самого визначника. За властивістю 9 визначників така алгебраїчна сума дорівнює нулю. Отже, 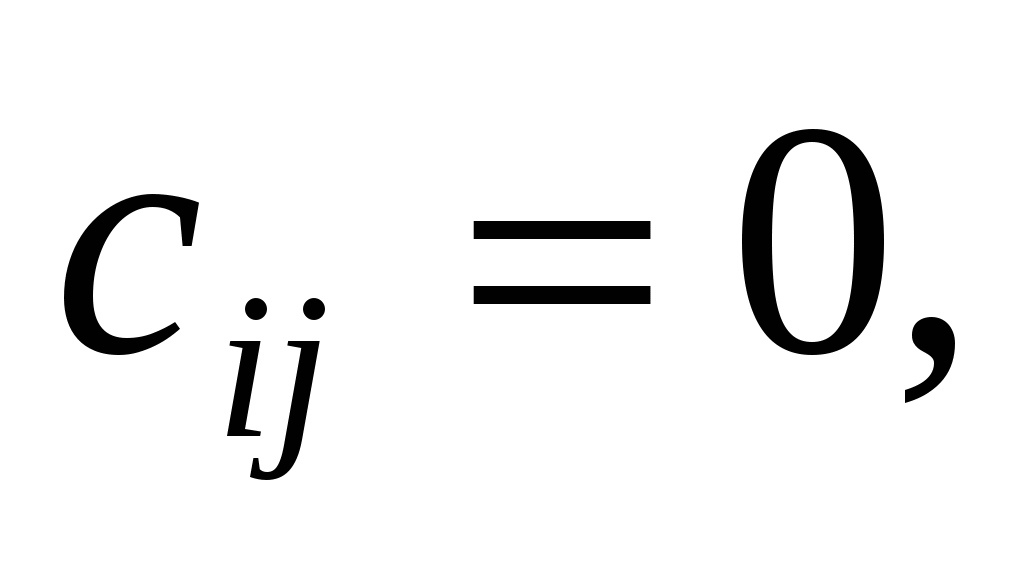 якщо i j. Матриця С набирає вигляду: якщо i j. Матриця С набирає вигляду: 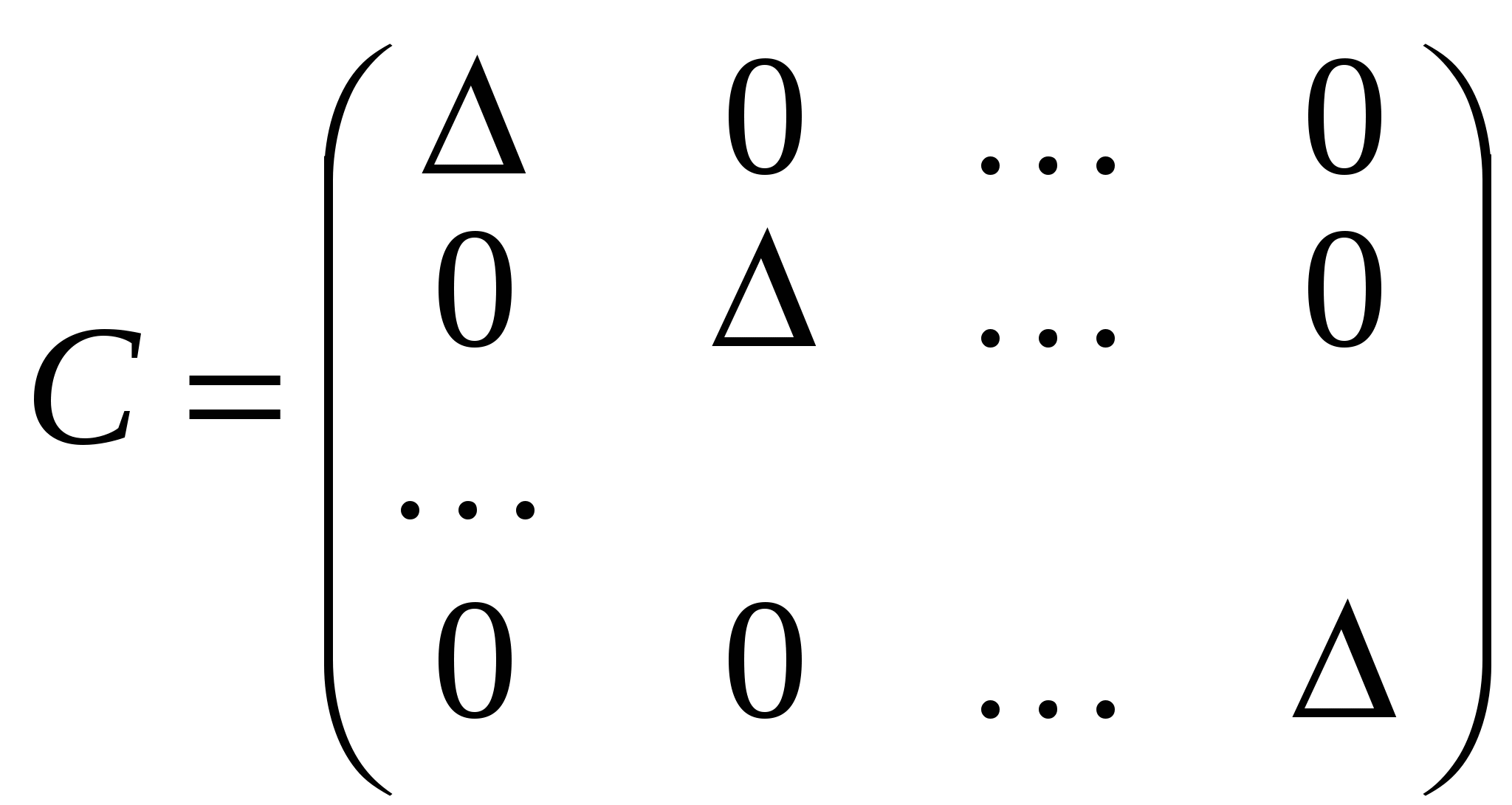 . Щоб ця матриця стала одиничною, треба помножити її на . Щоб ця матриця стала одиничною, треба помножити її на 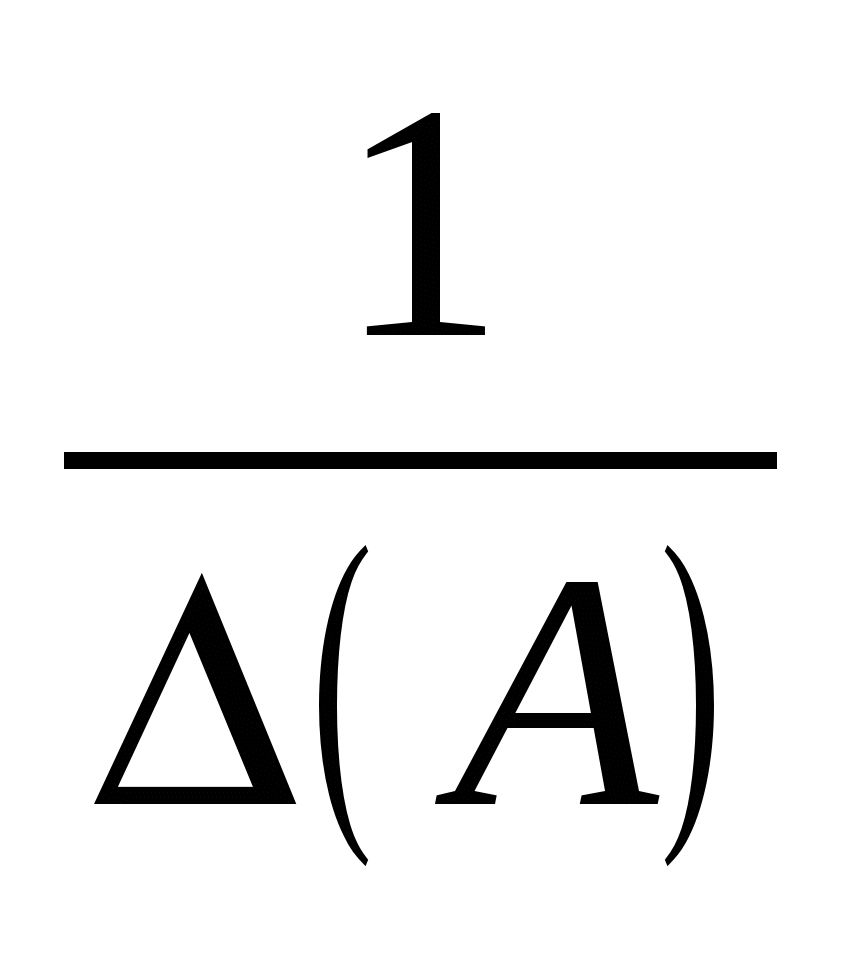 . .
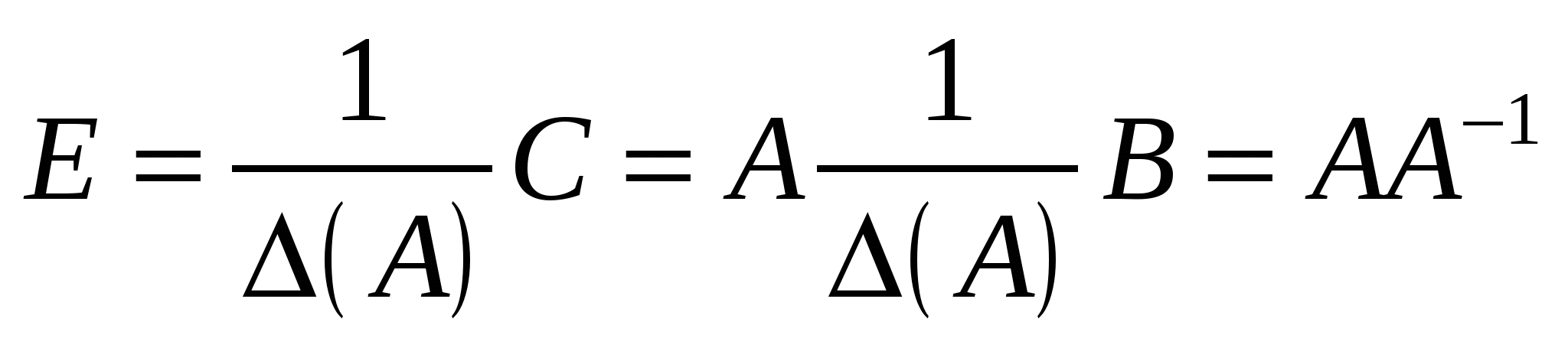 . .
Отже, обернена матриця має вигляд:
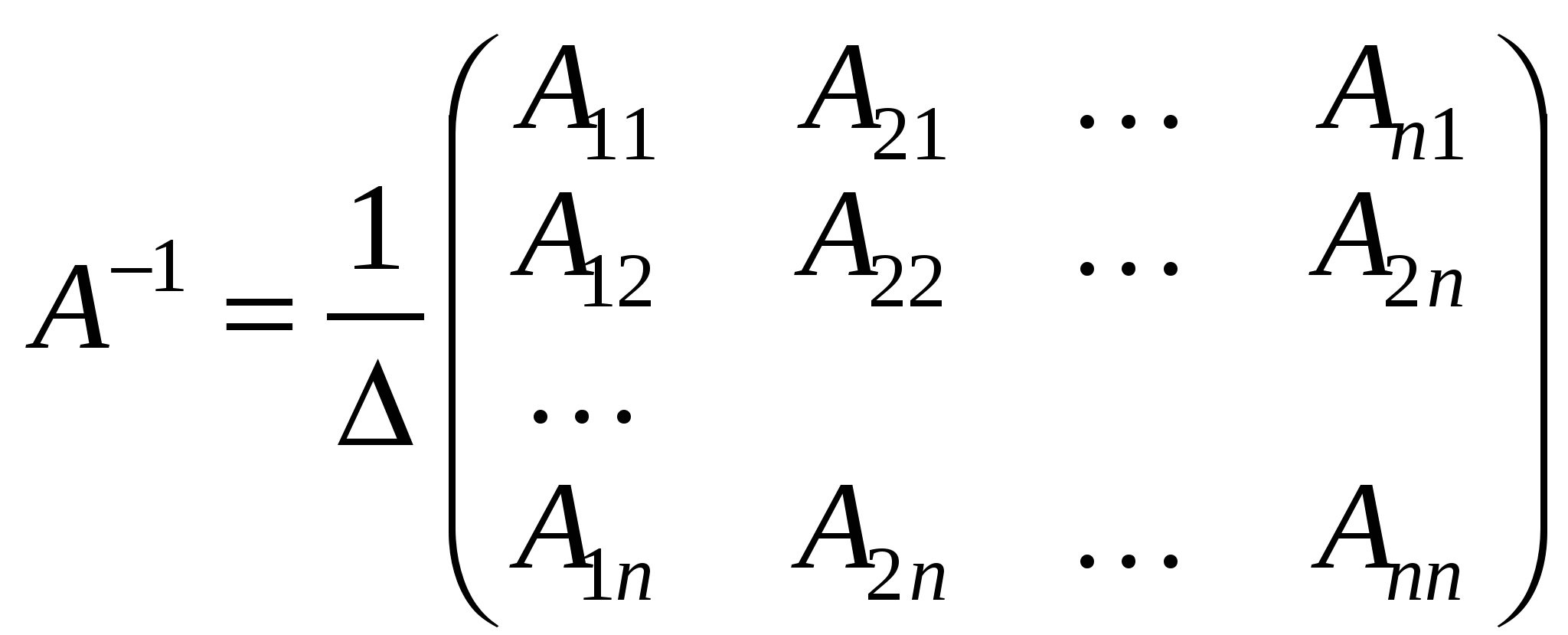 . .
Доведемо, що для матриці А матриця А–1 єдина. Для цього припустимо протилежне. Нехай існує одна матриця С, така що АС = СА = Е. Тоді
САА–1 = С(АА–1) = СЕ = С,
а водночас
САА–1 = (СА)А–1 = ЕА–1 = А–1, звідси С = А–1.
Доходимо висновку, що початкове припущення неправильне, тобто обернена матриця єдина.
Повернемось тепер до виразу (1.5) — запису системи рівнянь у матричному вигляді АХ = В. Припустимо, що система складається з n лінійних рівнянь з n невідомими, матриця А — квадратна і 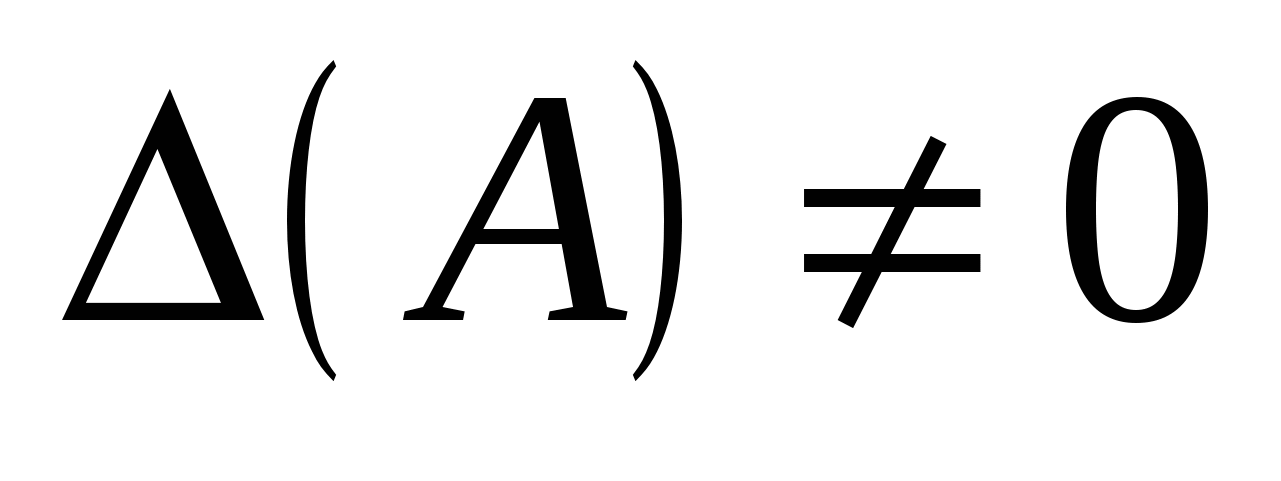 — матриця невироджена. Тоді для матриці А побудуємо обернену А–1 — вона за тих припущень, які щойно зроблено, існує. Помноживши тепер матричну рівність АХ = В зліва на матрицю А–1, дістанемо: — матриця невироджена. Тоді для матриці А побудуємо обернену А–1 — вона за тих припущень, які щойно зроблено, існує. Помноживши тепер матричну рівність АХ = В зліва на матрицю А–1, дістанемо:
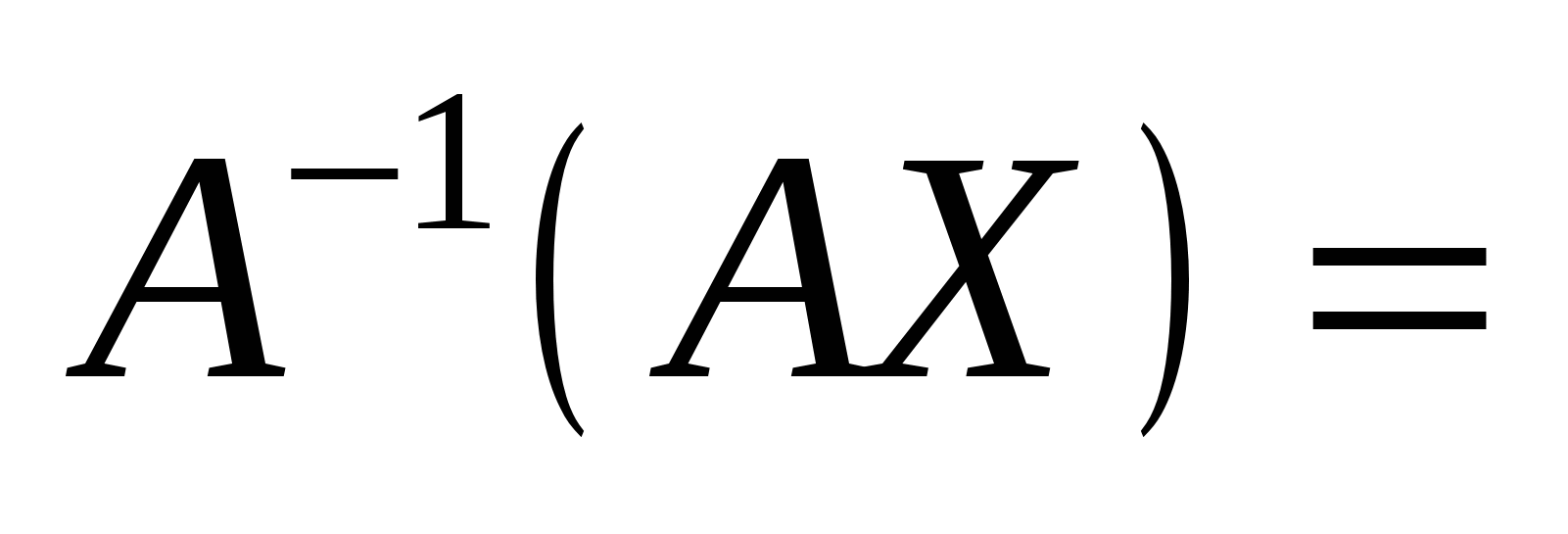 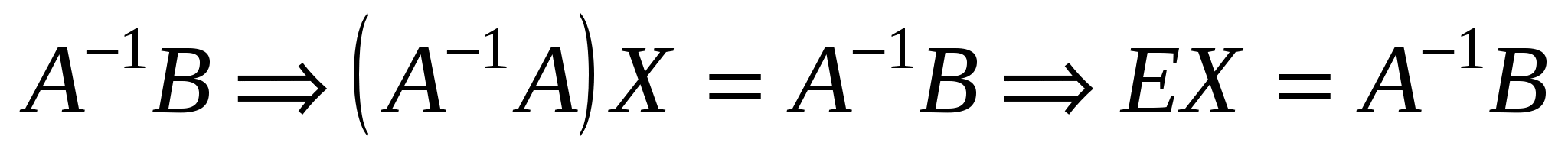 , ,
або остаточно 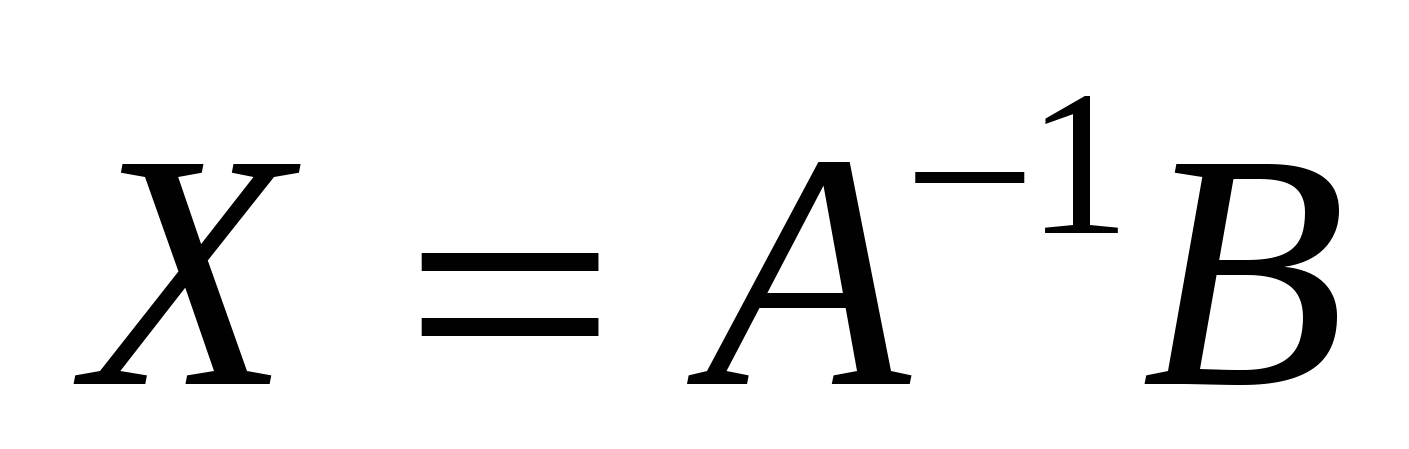 . .
Останній вираз — це розв’язок системи лінійних рівнянь. Зауважимо, що в такому вигляді можна записати розв’язок будь-якого матричного рівняння, якщо матриця А задовольняє умови існування А–1.
1.2.4. Ранг матриці
Розглянемо матрицю А розміром 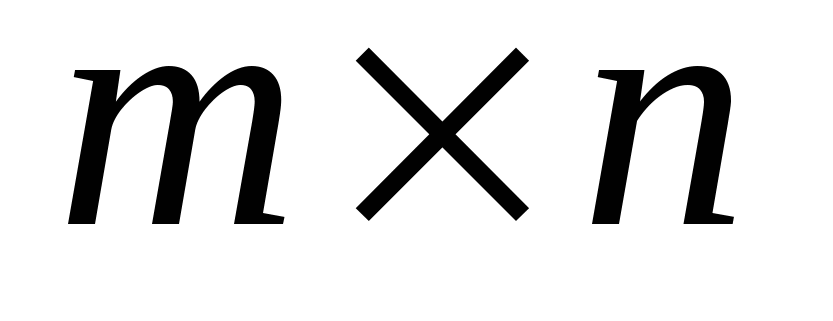
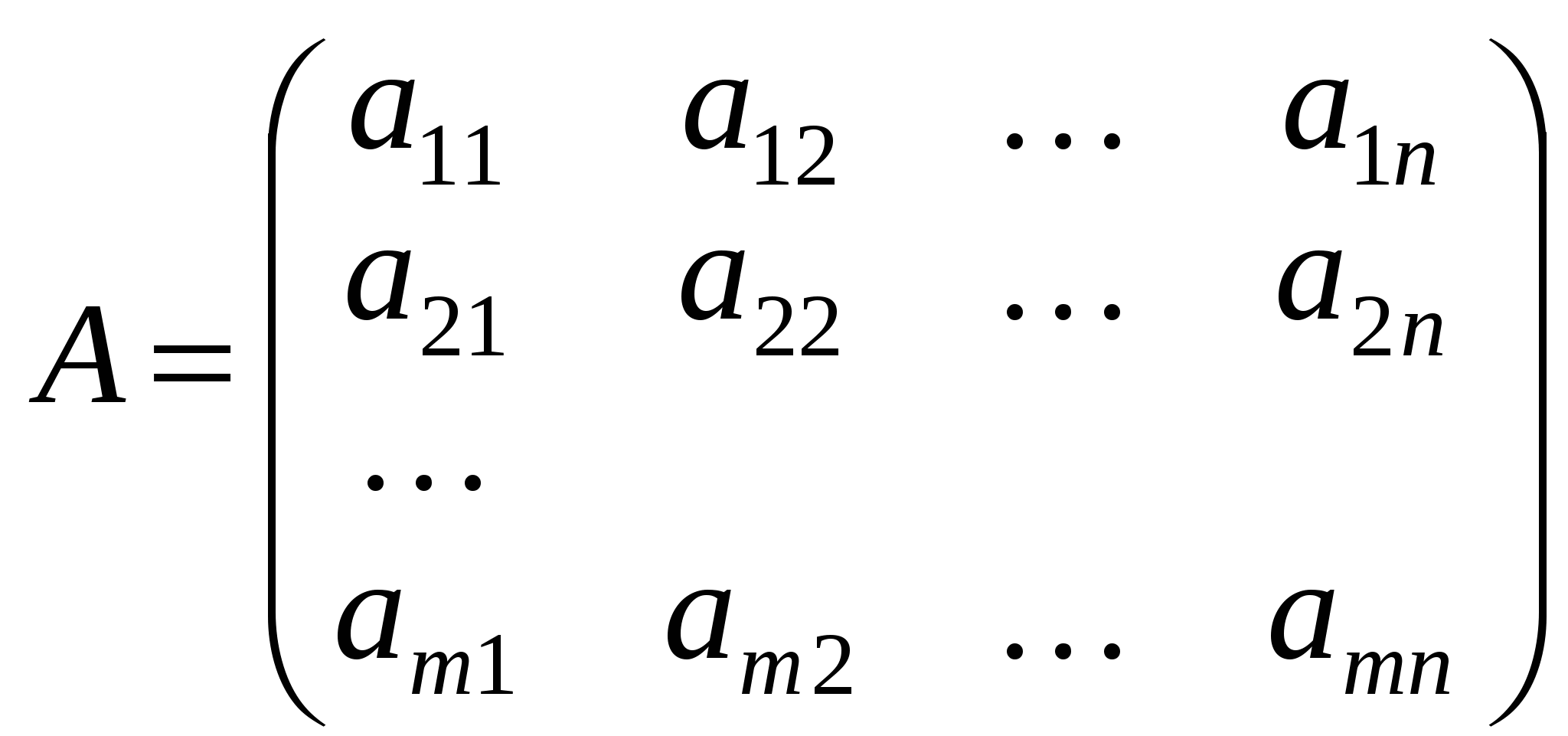
і введемо ще одне важливе поняття.
Означення. Рангом матриці А розміром 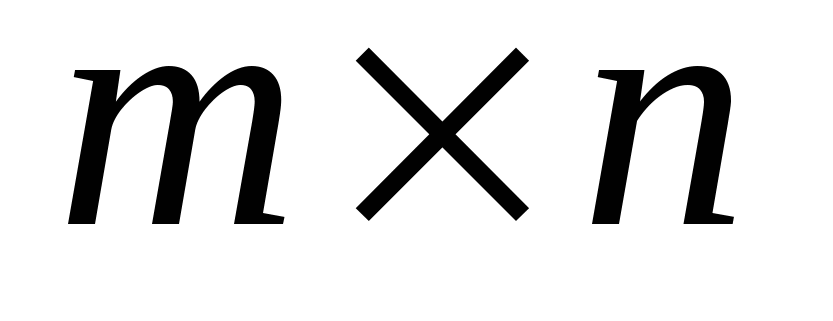 називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що 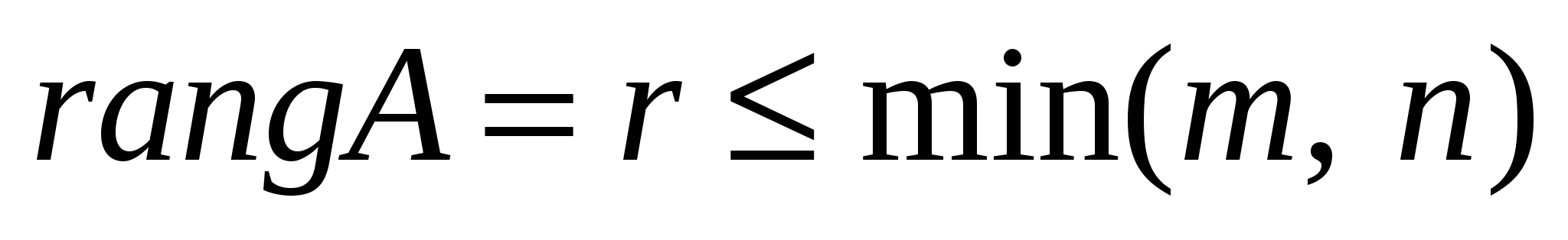 , а най- , а най-
більший можливий ранг матриці може дорівнювати меншому з чисел m і n.
Розглянемо також поняття обвідного мінора k-го порядку. Це буде такий мінор 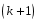 -го порядку, який повністю містить у собі мінор k-го порядку. -го порядку, який повністю містить у собі мінор k-го порядку.
Обчислюючи ранг матриці, потрібно переходити від мінорів менших порядків, відмінних від нуля, до мінорів більших порядків. Якщо вже знайдено відмінний від нуля мінор М k-го порядку, то достатньо обчислити лише мінори 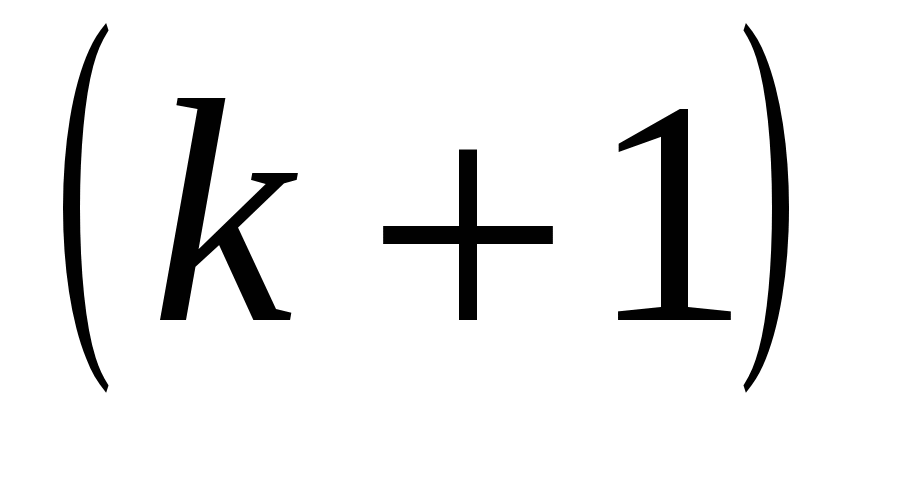 -го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори -го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори 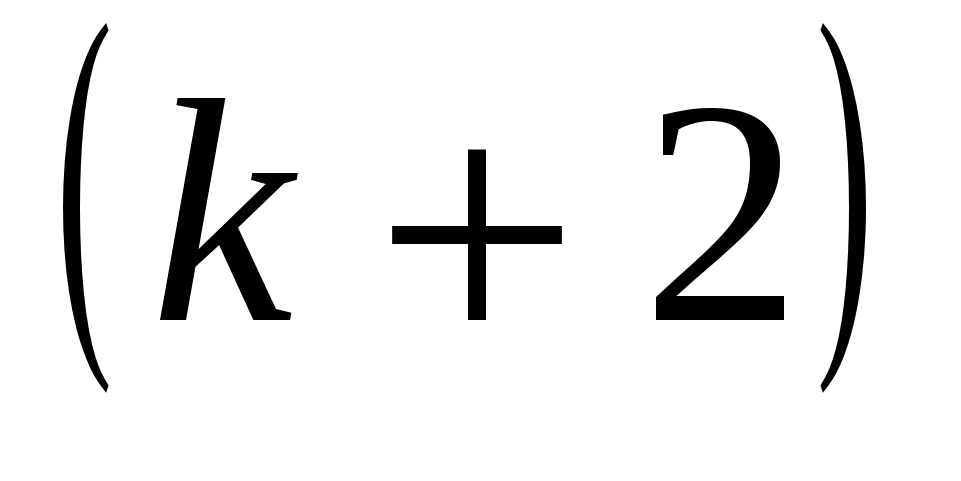 -го порядку і т. д. -го порядку і т. д.
Означення. Елементарними перетвореннями матриці А називаються такі її перетворення:
заміна місцями двох рядків або двох стовпців матриці;
множення рядка або стовпця матриці на довільне відмінне від нуля число;
додавання елементів одного рядка або стовпця до відповідних елементів іншого рядка або стовпця, попередньо помноженого на деяке число.
Теорема. Елементарні перетворення не змінюють рангу матриці.
Далі матриці, які мають рівні ранги, називатимемо еквівалентними матрицями. Еквівалентні матриці об’єднуватимемо знаком «» («тильда»).
План практичних занять
Освоєння дій з матрицями.
Побудова оберненої матриці.
Розв’язування систем рівнянь за допомогою оберненої матриці.
Відшукання рангу матриці.
|
|
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.