ТВиМС КР Хегай АС ДЭ-900 (2). Системы случайных величин. Элементы математической статистики
 Скачать 43.63 Kb. Скачать 43.63 Kb.
|
|
КОНРОЛЬНАЯ РАБОТА № 2 (Вариант 1) (спец. “Финансы и кредит” (080105), ускоренная форма обучения) ТЕМА: Системы случайных величин. Элементы математической статистики. Задача 1. Закон распределения системы двух дискретных случайных величин (Х, У) задан таблицей:
Найти: законы распределения случайных величин Х и У; условный закон распределения случайной величины Х, при условии, что У =1; 3) математические ожидания М(Х), М(У) и центр рассеивания; 4) дисперсии D(X), D(Y); 5) корреляционный момент Сху и коэффициент корреляции rxy. P(X=0)=0,05+0+0,1+0=0,15 P(X=1)=0,2+0,05+0+0,1=0,35 P(X=2)=0,1+0,05+0,05+0,05=0,25 P(X=3)=0+0,1+0,05+0,1=0,25 P(Y=-4)=0,35 P(Y=-3)=0,2 P(Y=-2)=0,2 P(Y=1)= 0,25 Законы распределения сл величин Х и У
Найдем условный закон распределения Х при условии, что У=1. Используем формулу Р(хi/yj) = 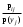 , p(Yj)=0,25 , p(Yj)=0,25Р(Х = х1 / Y = y4 )= 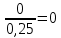 Р(Х = х2 / Y = y4 )=0,4 Р(Х = х3 / Y = y4 )=0,2 Р(Х = х4 / Y = y4 )=0,4 Условное распределение (X/Y = 1) имеет вид:
M(X)=0*0,15+1*0,35+2*0,25+3*0,25=0+0,35+0,5+0,75=1,6 D(X)= (0 – 1,6)20,15 + (1 – 1,6)20,35 + (2 – 1,6)20,25+ (3 – 1,6)20,25=0,384+0,126+0,04+0,49=1,04 σ(X)=1,02 M(Y)=-4*0,35-3*0,2-2*0,2+1*0,25=-1,4-0,6-0,4+0,25=-2,15 D(Y)= (-4 +2,15)20,35 + (-3+2,15)20,2 + (-2 +2,15)20,2+ (1 +2,15)20,25=1,197+0,144+0,0045+2,48=3,8 σ(Y)= 1,95 Таким образом, центром рассеивания является точка (1,02; 1,95). Cоставим таблицу системы центрированных случайных величин 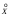 = Х – М(Х) = Х – 1,6; = Х – М(Х) = Х – 1,6; 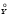 = Y – M(Y) = Y + 2,15 = Y – M(Y) = Y + 2,15
Cov (X,Y)=-1,60,05(-1,85) + (-1,6) 0,10,15 + (-0,6) 0,2(-1,85) +(-0,6) 0,05(-0,85) +(-0,6) 0,13,15 +0,40,1(-1,85) +0,40,05(-0,85) +0,40,050,15 +0,40,053,15 +1,40,1(-0,85) +1,40,050,15 +1,40,13,15=0,48-0,024+0,222+0,102-0,189-0,074-0,017+0,003-0,119+0,0105+0,441=0,8355 (Х, Y)= 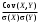 =0,8355/1,02*1,95=0,42 =0,8355/1,02*1,95=0,42Задача 2. Система двух непрерывных случайных величин (Х,У) имеет равномерное распределение в области D = (х,у) х2 + у2 1; 0 у 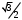 ; у -х ; у -х 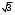 . .Найти: плотность распределения; вероятность Р[(Х,У) G] попадания в область G=(х,у) х2+у2 1; у 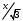 ; ;плотности распределения f1(x) иf2(x) случайных величин Х и У и условные плотности (х у) и (у х); математические ожидания М(Х), М(У) и центр рассеивания; дисперсии D(X), D(Y); корреляционный момент Сху и коэффициент корреляции rxy. Задача 3. В результате испытания случайная величина Х приняла следующие 16 значений:
Требуется: построить статистическое распределение; изобразить полигон распределения; построить эмпирическую функцию распределения; считая величину Х непрерывной, составить таблицу статистического распределения, разбив промежуток (0; 10) на 5 участков, имеющих одинаковые длины и построить гистограмму относительных частот. Задача 4. Даны 15 выборочных значений Х1, Х2, …Х15:
случайной величины Х, имеющей нормальный закон распределения с неизвестными параметрами а и 2. Требуется: вычислить точечные оценки а* и (2)* параметров а и 2, принимая а*= 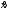 , (2)*= (а*(Х))2; записать функцию плотности и найти Р(Х2); , (2)*= (а*(Х))2; записать функцию плотности и найти Р(Х2);построить доверительные интервалы для параметров а и с надежностью 0,99; используя 2 – критерий и критерий согласия Колмагорова-Смирнова с уровнем значимости ε = 0,1, оценить согласованность эмпирического и теоретического законов распределения, разбив интервал ( 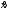 -1; -1; 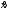 +1) на 5 равных частей. +1) на 5 равных частей.Задача 5. По данным корреляционной таблицы:
найти условные средние 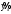 и и 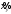 ; ;оценить тесноту линейной связи между случайными величинами Х и У, а так же обоснованность связи между этими величинами; составить уравнение линейной регрессии У по Х и Х по У; сделать чертеж, нанеся на него условные средние и прямые регрессии. |
