Сызықты жүйенің дұрыс еместік коэффициенті туралы. баяндамаға. Сызыты жйені дрыс еместік коэффициенті туралы
 Скачать 25.77 Kb. Скачать 25.77 Kb.
|
|
Сызықты жүйенің дұрыс еместік коэффициенті туралы 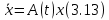 және 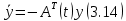 жүйелері түйіндес деп аталады. Олардың шешімдері скаляр көбейтіндісі 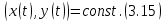 Анықтама. Келесі формуламен анықталатын 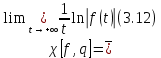 сан (немесе немесе символы), мұнда 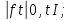 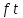 нақты функциясының жоғары Ляпунов сипаттауыш көрсеткіші, немесе қысқаша нақты функциясының жоғары Ляпунов сипаттауыш көрсеткіші, немесе қысқаша 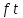 функциясының Ляпунов көрсеткіші деп аталады. функциясының Ляпунов көрсеткіші деп аталады.Анықтама. Егер оның сипаттамалық дәрежелерінің қосындысы басқа іргелі жүйелермен салыстырғанда ең кіші болса, іргелі жүйе қалыпты деп аталады. (3.13) сызықты жүйесінің базисі 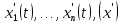 Ал осы базистердің Ляпунов көрсеткіші өсу ретімен орналасқан болса, онда 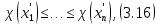 және түйіндес жүйелері үшін базисі 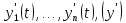 Ляпунов көрсеткіші кему ретімен орналасқан болса, онда 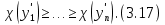 Кез келген 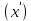 және және 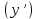 базистері үшін скаляр көбейтіндісі (және керісінше) табылатын болса, онда базистері үшін скаляр көбейтіндісі (және керісінше) табылатын болса, онда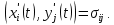 мұндай базитер өзара деп аталады. Өзара базистердің осындай қасиеті бар 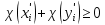 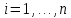 . Сондықтан . Сондықтан 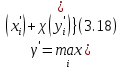 саны теріс емес. Ол өзара базистердің ақауы деп аталады. Сызықты жүйе (3.13) және оған түйіндес (3.14) жүйенің өзара сәйкес базистерінің барлық мүмкін жұптары бойынша алынған ақаулардың минимумы 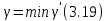 (3.13) және (3.14) жүйелердің дұрыс еместік коэффициенті деп аталады. Бұл анықтамаға сәйкес, ол өзара базистерді таңдауға тәуелді емес және, демек, жүйелердің өздерінің қасиеттерімен толығымен анықталады. Бірақ олардың әрқайсысы бір-бірімен бірегей түрде анықталатындықтан, ретсіздік коэффициенті түсінігін осы жүйелердің біреуімен ғана байланыстыруға болады. Мысал 1. 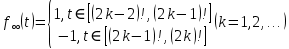 функциясын пайдаланайық. Бұл функцияны 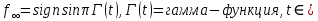 деп анықтауға болатыны белгілі. 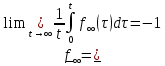 , , 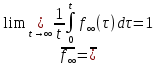 ; ;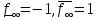 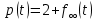 Келесі сызықты диагоналдық дифференциалдық теңдеулер жүйесін қарастырамыз 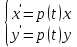 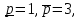 яғни 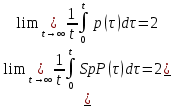 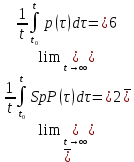 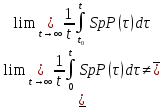 болғандықтан 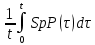 функциясының дәл шегі жоқ, олай болса функциясының дәл шегі жоқ, олай болса қажетті шарт орындалмағандықтан қарастырып отырған сызықты дифференциалдық теңдеулер жүйесі дұрыс жүйе болмайды. 2.2. Түйіндес кеңістіктердегі көрсеткіштер мен базистердің қасиеттері. Ең алдымен 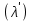 және және 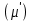 сандары арасында сәйкестік болған кезде пайда болатын және бұл сандардың шығу тегіне қатысы жоқ элементар теңсіздіктерге негізделген қасиеттерді қарастырайық. сандары арасында сәйкестік болған кезде пайда болатын және бұл сандардың шығу тегіне қатысы жоқ элементар теңсіздіктерге негізделген қасиеттерді қарастырайық.Кейбір 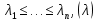 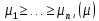 сандары берілсін және олардың арасындағы 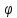 жеке сәйкестік жеке сәйкестік  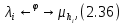 немесе, бұл бірдей , олардың индекстері арасындағы ауыстыру берілген  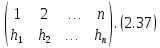 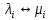 бірдей алмастырумен 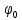 сәйкестігін тура деп атаймыз. сәйкестігін тура деп атаймыз.Біз көрсеткіштерге қатысты қолданылған терминологияны ұстанамыз. Сонымен, егер 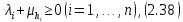 болса, 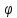 сәйкес келсе түйіндес шарты орындалады дейміз; сәйкес келсе түйіндес шарты орындалады дейміз; 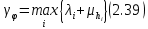 санын кемістік, ал 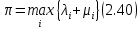 санын Перрон коэффициенті деп атаймыз. 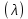 және және 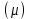 сандарының өзі әрі қарай дәреже көрсеткіші деп аталады, ал егер сандарының өзі әрі қарай дәреже көрсеткіші деп аталады, ал егер 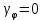 болса, онда біз оларды дұрыс деп айтамыз. Төмендегі айқын ескертуге сүйене отырып, олардың қасиеттерін зерттеуге көшейік. болса, онда біз оларды дұрыс деп айтамыз. Төмендегі айқын ескертуге сүйене отырып, олардың қасиеттерін зерттеуге көшейік.2.6.1. 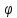 ақырлы ақырлы 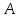 және және 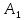 жиындары арасындағы жеке сәйкестік болсын, ал жиындары арасындағы жеке сәйкестік болсын, ал 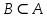 және және 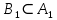 ішкі жиындары бірдей элементтер санынан құралсын. Егер ішкі жиындары бірдей элементтер санынан құралсын. Егер 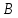 элементінің кем дегенде бір элементі элементінің кем дегенде бір элементі 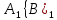 -ге салыстырылған болса, онда -ге салыстырылған болса, онда 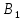 -дің кем дегенде бір элементі -дің кем дегенде бір элементі 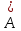 -ге сәйкестендіріледі. -ге сәйкестендіріледі.2.6.2. Салдар. Егер (2.37) алмастыруда 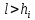 болатындай болатындай 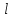 бар болса, онда бар болса, онда 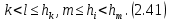 болатындай 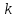 және және 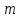 да бар. Сол сияқты, егер да бар. Сол сияқты, егер 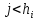 бар болса, онда бар болса, онда 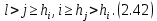 де бар. 2.6.3. Кез келген 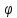 сәйкестігі үшін бізде сәйкестігі үшін бізде 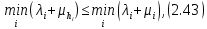 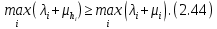 2.6.4. Егер түйіндес шарты кем дегенде бір 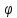 сәйкестігі үшін орындалса: сәйкестігі үшін орындалса: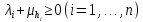 онда ол тура сәйкестікте одан да көп болады: 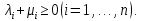 Бұл (2.43) мәнінен шығады. 2.6.5. Кез келген сәйкестік үшін 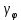 кемістігі және кемістігі және 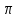 Перрон коэффициенті Перрон коэффициенті 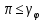 теңсіздігіне, ал түйіндес шарты орындалса, теңсіздігіне, ал түйіндес шарты орындалса, 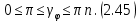 теңсіздіктеріне бағынады. Шынында да, біріншісі (2.44) сәйкес келеді, ал екіншісі 2.6.4-тен және келесі теңсіздікке сәйкес келеді, бұл түйіндестік шартында дұрыс: 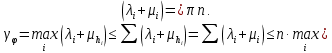 .2.3. Тұрақты емес сызықтық бөлігі бар сызықты емес жүйелер үшін орнықтылық критерийі Нақты сызықтық біртекті жүйені қарастырайық 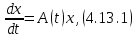 мұндағы 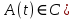 , , 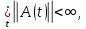 және және 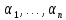 оның сипаттамалық көрсеткіші болсын. оның сипаттамалық көрсеткіші болсын.Анықтама. 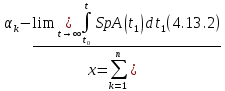 Саны (4.13.1) жүйенің дұрыс еместігінің өлшемі деп аталады [6]. Ляпунов теңсіздігіне байланысты 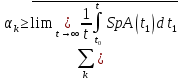 (4.13.2) формуласынан аламыз 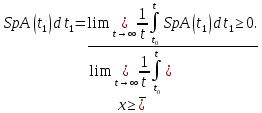 (4.13.1) жүйесі x=0 болған жағдайда ғана дұрыс болатыны анық. Тұрақты емес жүйелердің Ляпунов критерийін жалпылауды Н.Г.Четаев жүргізді. Ляпунов пен Четаев теоремасын жалпылайтын Массердің [7] нәтижесін ұсынамыз [6]. Массер теоремасы. Сызықты емес жүйе берілсін, 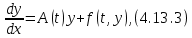 мұндағы 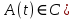 , , 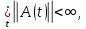 және және 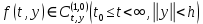 және және 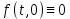 . .Егер 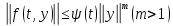 , ,мұндағы 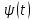 оң функция, оң функция, 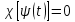 , ,(4.13.1) сызықтық жуықтауының 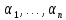 сипаттамалық көрсеткіші үшін теңсіздік сипаттамалық көрсеткіші үшін теңсіздік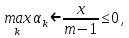 мұндағы 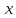 – (4.13.1) сәйкес сызықтық жүйенің дұрыстық өлшемі, онда сызықты емес жүйенің – (4.13.1) сәйкес сызықтық жүйенің дұрыстық өлшемі, онда сызықты емес жүйенің 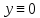 тривиальды шешімі (4.13.3) тривиальды шешімі (4.13.3) 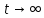 ретінде Ляпунов асимптотикалық тұрақты. ретінде Ляпунов асимптотикалық тұрақты. |
