Контрольная работа (физика горных пород). Контрольная. Скорость распространения упругих продольных V
 Скачать 3.22 Mb. Скачать 3.22 Mb.
|
|
Задача 16 Укажите зависимость скорости распространения продольных и поперечных волн от упругих свойств горных пород и размеров образца. При испытаниях горной породы на срез со сжатием в шахтных условиях получены следующие результаты: при углах среза 60; 45; 30 градусов прочность на срез составила, соответственно, 10; 25; 35 Мпа. Построить паспорт прочности и определить величину сцепления массива горных пород. Скорость распространения упругих продольных - Vp и поперечных - Vs волн зависит от упругих характеристик пород: 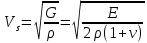 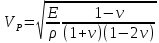 где 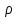 – плотность породы; – плотность породы;Е – модуль Юнга; 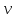 – коэффициент Пуансона; – коэффициент Пуансона;G – модуль сдвига. 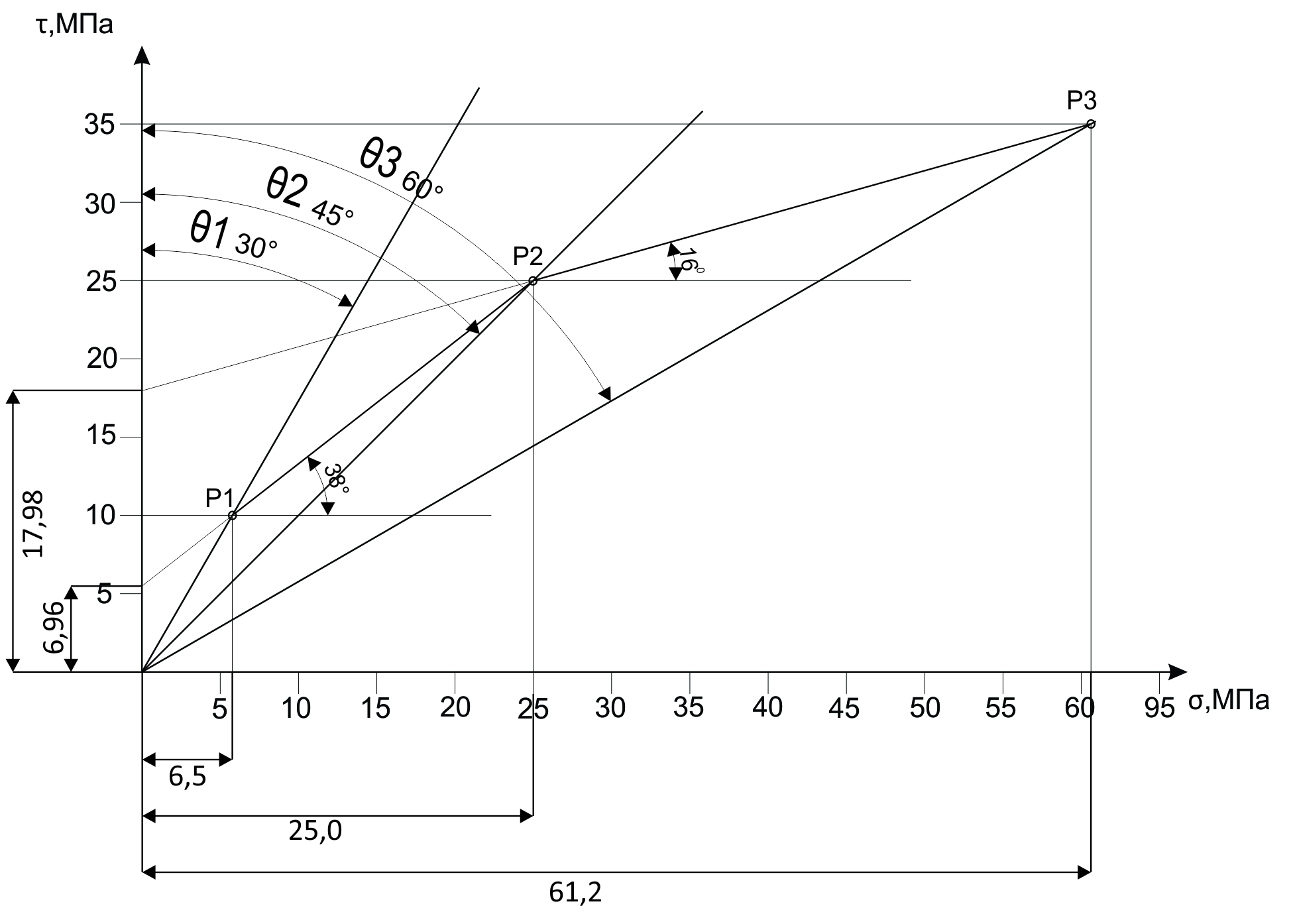 Сцепление 6,96 Мпа для отрезка Р1-Р2, 17,98 Мпа для отрезка Р2-Р3. Задача 19 Дайте сравнительную оценку статического и динамического методов определения упругих свойств горных пород. При проходке горной выработки сечением 8 м2продвигание забоя за цикл составляет 2 м. Сколько вагонеток вместимостью 1,5 м3 потребуется для уборки взорванной породы, если её коэффициент разрыхления – 1,8? Статический метод заключается в медленном нагружении образца горной породы на прессе с параллельным замером продольной и поперечной деформаций с помощью специальных датчиков - тензометров, По результатам испытаний производится построение деформационной кривой, зятем по линейному участку графика определяются модуль упругости и коэффициент Пуассона.Метод считается классическим, поскольку он основан на непосредственном измерении напряжений и деформаций горной породы, однако он требует значительных затрат труда и времени, связанных с тщательностью изготовления образцов правильной формы и установки измерителей деформации (датчиков). Кроме того, метод практически невозможно реализовать в производственных условиях на массиве горных пород. Динамический метод в значительной степени свободен от этих недостатков. Существо метода состоит в измерении скорости распространения упругой волны в горных породах (как правило, в ультразвуковом диапазоне) и последующем вычислении упругих свойств пород по формулам. Наличие компактной переносной аппаратуры позволяет быстро и точно определять характеристики пород в производственных условиях. Таким образом, динамический импульсный метод более прост в исполнении, но при этом необходимо учитывать следующие обстоятельства. Используемые для вычисления формулы, строго говоря, справедливы для идеально упругих, однородных и сплошных сред. Чем больше реальная горная порода отличается от этой идеальной модели, тем значительнее ошибки метода. Впрочем, для большинства задач реальной горной практики возможные ошибки не превышают допустимых. С другой стороны, упругие характеристики одной и той же горной породы, измеренные статическим и динамическим методами, существенно различаются по величине. Это обусловлено следующими факторами: 1. Явление упругого последействия. Сопротивляясь внешним нагрузкам, горная порода изменяет свою температуру. При сжатии она стремится увеличить расстояние между атомами, т.е. нагревается. При растяжении - напротив, она охлаждается. При медленном (статическом) нагружении происходит теплообмен с окружающей средой и деформации соответствуют закону Гука. При быстром (динамическом) нагружении теплообмен происходить не успевает и измеряемая деформация меньше, чем при статических испытаниях. Следовательно, динамический модуль упругости больше статического. 2. Влияние дефектов структуры. При быстром нагружении дефекты структуры (точечные, линейные и объемные) не успевают включиться в процесс деформирования, и горная порода проявляет себя как менее дефектное тело, чем есть на самом деле. Отсюда динамическая упругость выше статической. 3. Релаксация напряжений. При нагружении породы с малой скоростью напряжения во времени перераспределяются с упругих элементов на менее упругие, что приводит к снижению общего уровня напряжений. Поэтому статический модуль упругости меньше по величине, чем динамический. Обьём взорванной породы: 8 м2 (сеч.выраб.) × 2 м (подв. забоя) × 1,8 (коэфф. разр.) = 28,8 м3 Количество вагонеток: 28,8 м3 (обьём породы) / 1,5 м3 (вмест. вагонетки) = 19,2 ≈ 20 вагонеток Задача 34 Дайте определение теплоёмкости горных пород. Как она зависит от температуры и влажности пород? Разрушение кубического образца горной породы со стороной 5 см произошло при вертикальной нагрузке 8 тонн и боковой – 5 тонн. Определить предельное касательное напряжение, действовавшее в площадке под углом 300 к горизонтальной плоскости. Теплоёмкостью породы называется количество тепла, необходимое для повышения на 1 градус температуры одного килограмма породы. 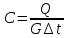 где 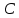 – теплоёмкость породы; – теплоёмкость породы;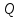 – количество переданного породе тепла; – количество переданного породе тепла;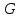 – вес породы; – вес породы;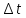 – изменение температуры. – изменение температуры.Установлено, что с увеличением влажности и температуры теплоемкость пород возрастает. Определение касательного напряжения: 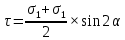 где 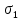 – вертикальная нагрузка, МПа; – вертикальная нагрузка, МПа;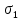 – боковая нагрузка, МПа; – боковая нагрузка, МПа;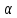 – угол к горизонтальной плоскости. – угол к горизонтальной плоскости.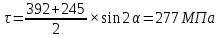 Задача 36 Опишите тепловое расширение и возникновение термических напряжений в горных породах. На расстоянии 20 м от источника энергия (амплитуда) упругой волны уменьшилась в 5 раз. Определить коэффициент затухания волны для данных условий. При изменении температуры неоднородных твердых тел, какими являются горные породы, на границах минеральных зерен возникают локальные термические напряжения (структурные термические напряжения) в связи с неодинаковым значением коэффициентов теплового расширения и модуля упругости различных минералов. При достижении этими напряжениями предельных значений происходит разрыв междузерновых связей, что приводит к тепловому расширению горных пород. Структурные термические напряжения в горных породах с изменением температуры не могут увеличиваться беспредельно. Максимальное их количество равно пределу прочности. Тепловое расширение (сужение) имеет место как при их нагреве, так и при их охлаждении. Тепловое расширение (сужение) горных пород начинает проявляться при температуре ±353-373 К (80-100˚С). До этих температур расширение породы происходит только за счет расширения только слагающих минералов. Выше этих температур структурные термические напряжения на границах отдельных минеральных зерен достигают предельных значений, что приводит к разрыву межзерновых связей на границах этих зерен, а увеличение размеров образца горной породы происходит при этом скачкообразно. В начале теплового расширения абсолютная величина отдельных скачков максимальна, а интервалы температур между смежными скачками относительно велики. С увеличением температуры частота скачков увеличивается, а абсолютное их значение уменьшается. Определение коэффициента затухания колебаний: 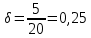 Задача 40 Что представляют собой диэлектрические потери в горных породах? Модуль пластичности горной породы составляет 25 ГПа, предел упругости – 40 МПа. Определить прочность при сжатии данной породы, если при её разрушении общая относительная продольная деформация составила 0,0015, а упругая – 0,0005. Построить график деформации. Электронная поляризация происходит практически мгновенно. Для завершения же последующих видов поляризации требуется все большее время (время релаксации). Поэтому с увеличением частоты переменного электрического поля все больше механизмов поляризации не успевает сработать и суммарный вектор поляризации уменьшается. При этом за счет запаздывания медленных видов поляризации увеличивается кинетическая энергия колебаний ионов и молекул в узлах кристаллической решетки, что сопровождается нагреванием горной породы. Та часть энергии электрического поля, которая расходуется на нагрев горной породы, называется диэлектрическими потерями. Определение прочности при сжатии: 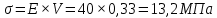 где 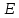 – предел упругости, МПа; – предел упругости, МПа;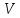 – коэффициент Пуассона; – коэффициент Пуассона;Расчёт коэффициента Пуансона 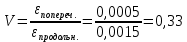  График деформации Задача 51 Опишите процедуру построения графика прочности глинистых пород. Определить объёмную теплоёмкость горной породы, если на цилиндрическом образце диаметром 6 см, высотой 15 см, и массой 1,2 кг определена удельная теплоёмкость 700 Дж/Кг*К. Глинистая порода в пластичном состоянии сопротивляется как растяжению, так и сжатию. Однако хрупкого разрушения (как скальные породы) глина не проявляет, поэтому зафиксировать разрушающую нагрузку при испытаниях глин невозможно. Поэтому принято считать прочностью глинистых пород при сжатии такое напряжение, при котором линейный размер образца уменьшается в два раза. Сложнее с прочностью при растяжении. При удлинении глинистая порода образует «шейку», вследствие чего площадь поперечного сечения образца непрерывно меняется, и величина прочности становится неопределенной. Поэтому построение паспорта прочности глинистых пород производится путем испытания их на срез со сжатием. Задавая ступенчато нормальное сжимающее напряжение, с помощью специальной матрицы определяется критическое срезающее напряжение. Откладывая точки, соответствующие этим напряжениям, определяют положение огибающей кругов напряжений Мора. Пористая нагрузочная плита обеспечивает удаление из глины отжатой воды. Особенностью паспорта прочности глинистых пород является более выпуклая, чем для скальных пород, огибающая кругов Мора. Определение объёмной теплоёмкости:  где  – удельная теплоёмкость, Дж/Кг*К; – удельная теплоёмкость, Дж/Кг*К; – плотность породы, кг/м3. – плотность породы, кг/м3.Расчёт плотности породы:  где  – масса образца, кг; – масса образца, кг; – обьем образца, м3. – обьем образца, м3.Объём образца:  где 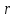 – радиус основания, м; – радиус основания, м;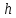 – высота образца, м. – высота образца, м. |
