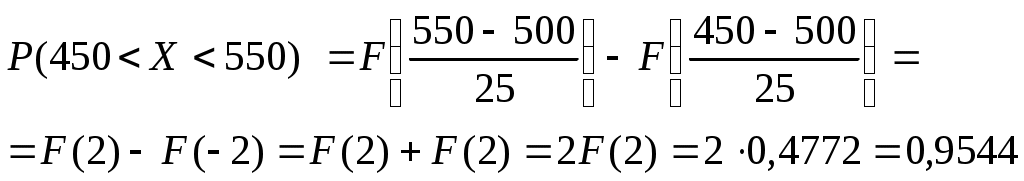Решение задач по теме Вероятность попадания х в заданный интервал. Решение Задач по теме Вероятность значения в интервале. Следующие задачи решаются по этому алгоритму
 Скачать 60 Kb. Скачать 60 Kb.
|
|
1. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 300 и среднеквадратическим отклонением 25. Найти вероятность того, что значение случайной величины Х окажется в пределах от 275 до 325.
2. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 500 и среднеквадратическим отклонением 25. Найти вероятность того, что значение случайной величины Х окажется в пределах от 450 до 550.
Следующие задачи решаются по этому алгоритму: 3. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 300 и среднеквадратическим отклонением 25. Найти вероятность того, что значение случайной величины Х окажется в пределах от 225 до 375. 4. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 500 и среднеквадратическим отклонением 15. Найти вероятность того, что значение случайной величины Х окажется в пределах от 485 до 515. 5. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 30 и среднеквадратическим отклонением 2,5. Найти вероятность того, что значение случайной величины Х окажется в пределах от 27,5 до 32,5. 6. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 50 и среднеквадратическим отклонением 2,5. Найти вероятность того, что значение случайной величины Х окажется в пределах от 45,0 до 55,0 7. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 3 и среднеквадратическим отклонением 0,25. Найти вероятность того, что значение случайной величины Х окажется в пределах от 2,25 до 3,75. 8. Случайная величина Х подчиняется нормальному закону распределения с математическим ожиданием 5,00 и среднеквадратическим отклонением 0,15. Найти вероятность того, что значение случайной величины Х окажется в пределах от 4,85 до 5,15 9. Записать функцию распределения и плотность вероятностей для нормально распределённой случайной величины, если М(Х)=-2, D(Х)=9. Решение: 1) Плотность вероятностей для нормального распределения случайной величины имеет вид 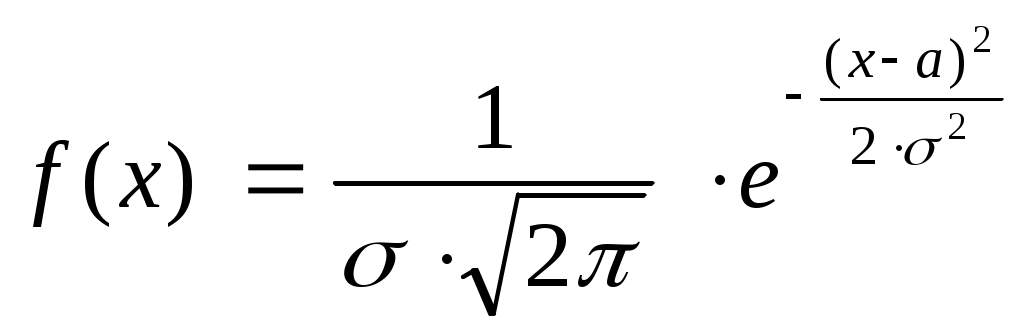 - функция Гаусса. - функция Гаусса.где а – математическое ожидание М(Х); – среднее квадратичное отклонение случайной величины Х, В нашем случае 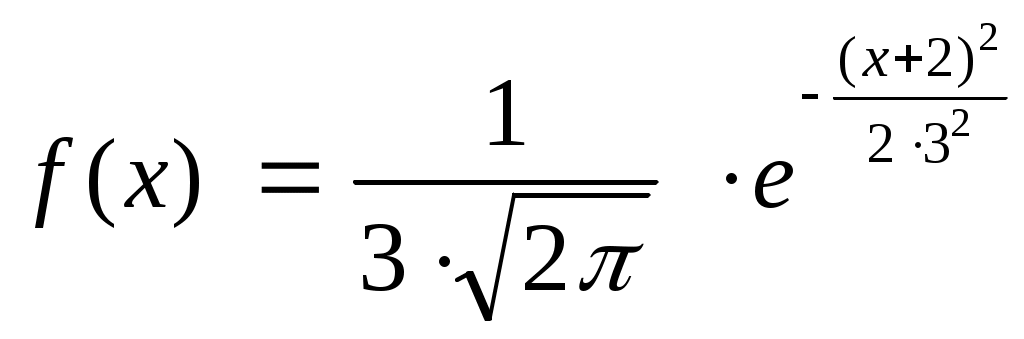 . .2) Функция распределения для нормально распределённой случайной величины это функция Лапласа 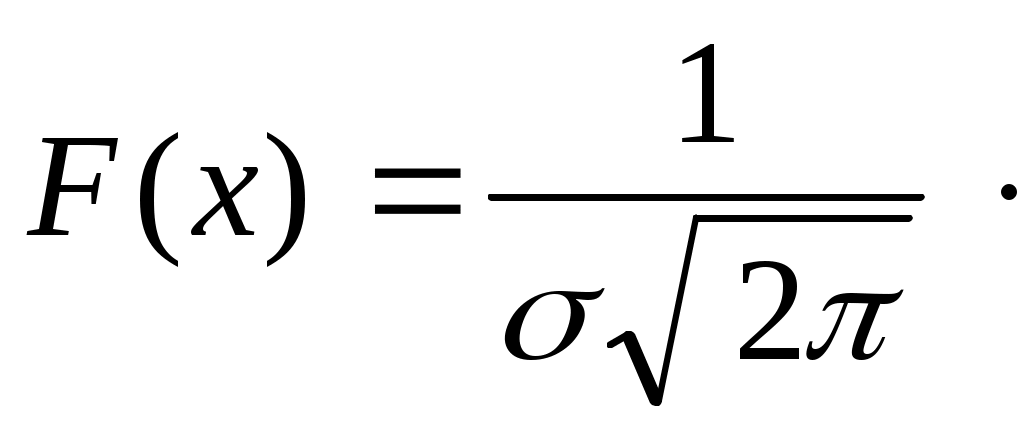 В нашем случае 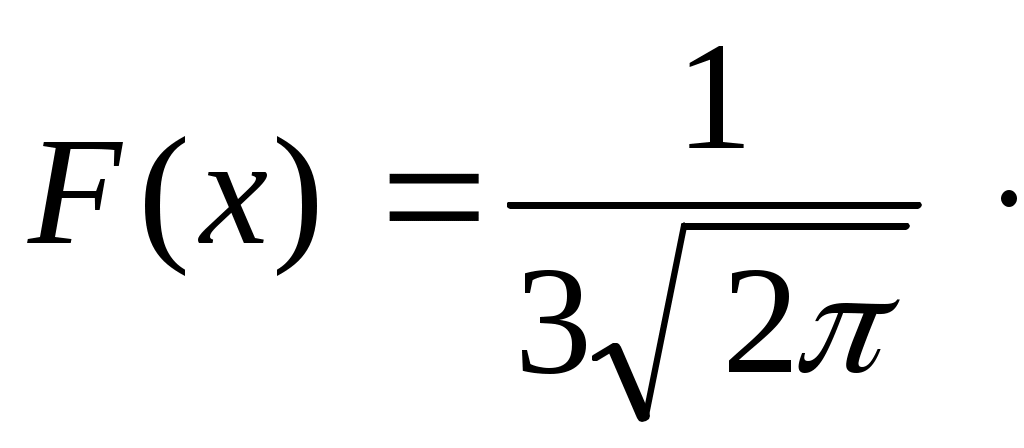 |

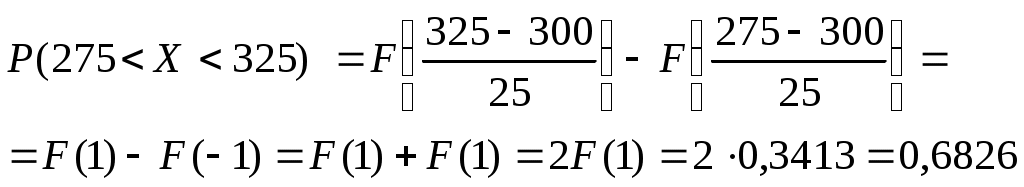
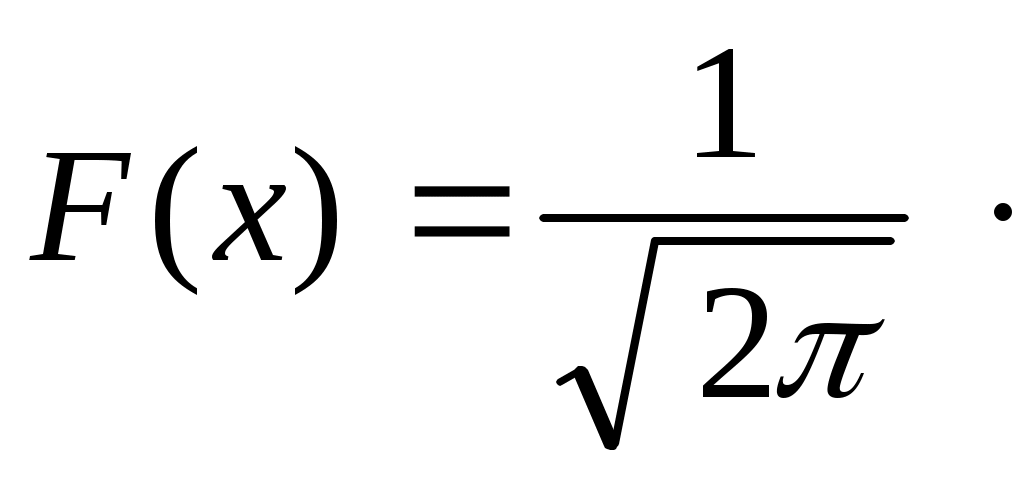
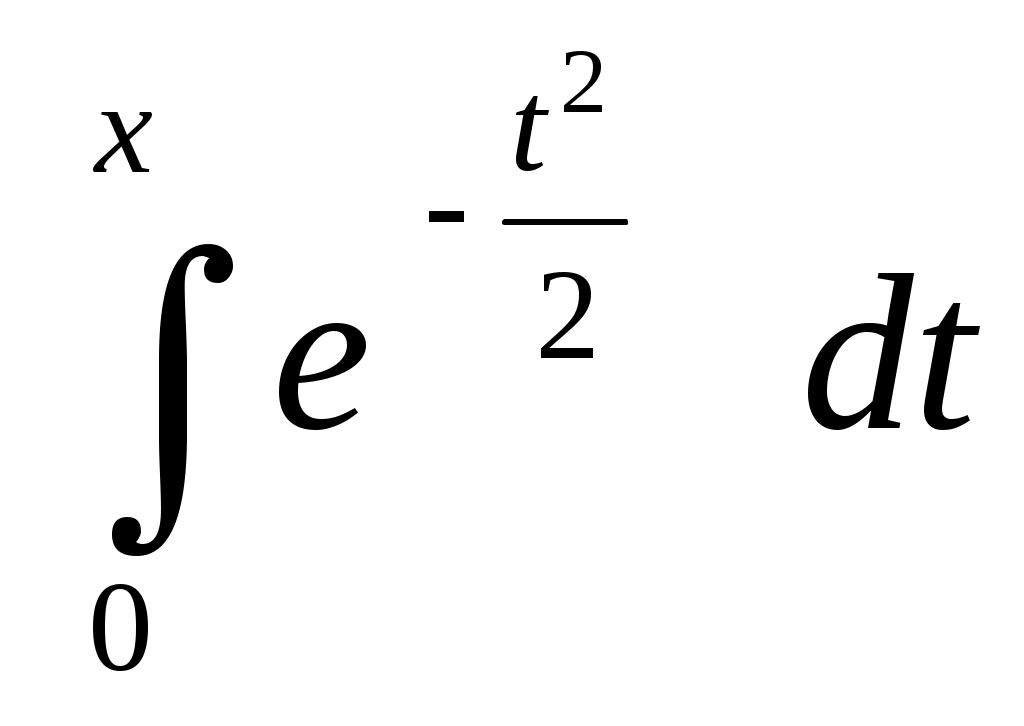 , при условии, что
, при условии, что