да. сопромат 1. Сложное сопротивление. Сложное сопротивление
 Скачать 280.45 Kb. Скачать 280.45 Kb.
|
|
Сложное сопротивление. Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения. Косой изгиб. Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса. В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.  Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения. Условие прочности при косом изгибе: 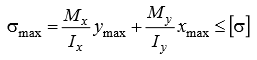 где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси. Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности: 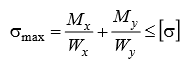 где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей. Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям. Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей: Изгиб с растяжением (сжатием). При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M. Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса: 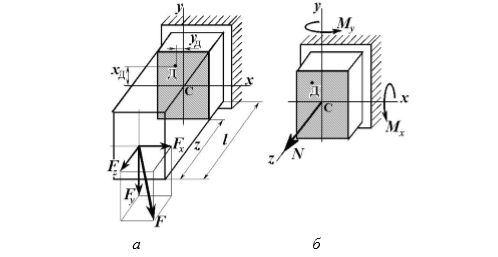 К расчёту на прочность бруса при изгибе с растяжением: a - нагружение бруса; б - внутренние силовые факторы в поперечном сечении; Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид: 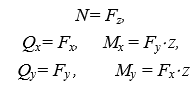 Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле: 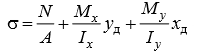 где А — площадь поперечного сечения. Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле: 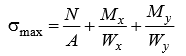 Условие прочночти имеет вид: Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям. Внецентренное растяжение или сжатие. При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса. 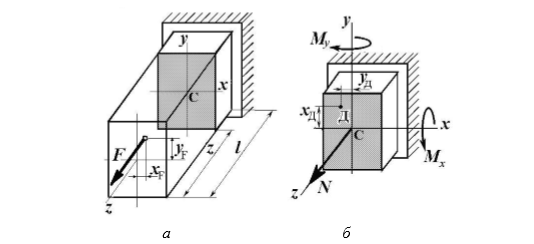 К расчёту на прочность бруса при внецентренном растяжении a - нагружение бруса; б - внутренние силовые факторы в поперечном сечении; Приведём силу F к центру тяжести:  где уF , xF — координаты точки приложения силы F. В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле: 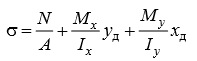 Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид: 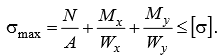 Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям. Кручение с изгибом. Сочетание деформаций изгиба и кручения характерно для работы валов машин. 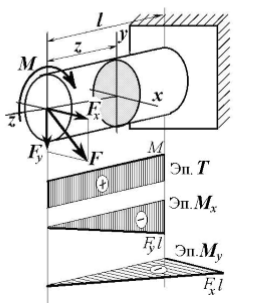 Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения: 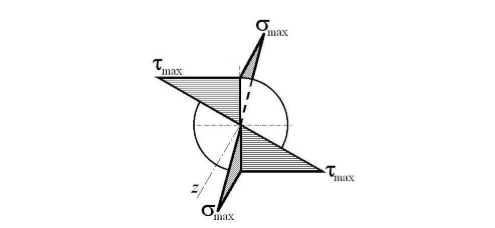 Эпюры напряжений в сечении бруса при кручении с изгибом Нормальное напряжение достигает максимума на поверхности: 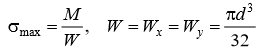 Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала: 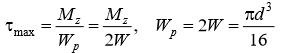 Из третьей и четвёртой теории прочности: 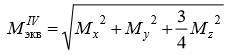 При кручении с изгибом условие прочности имеет вид: |
