вфв. 26 вариант. Внутренние силовые факторы возникающие в поперечном сечении тела
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОЗДУШНО-КОСМИЧЕСКИЕ СИЛЫ Федеральное государственное казенное военное профессиональное образовательное учреждение «183 учебный центр» Министерства обороны Российской Федерации КУРСОВАЯ РАБОТАна тему: ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ВОЗНИКАЮЩИЕ В ПОПЕРЕЧНОМ СЕЧЕНИИ ТЕЛА курсант: ______________________________ (фамилия, инициалы, подпись) руководитель: _________________________ Дата защиты: " ____ " ____________ 20__г. Оценка: _____________________________ Подписи членов комиссии: ______________________________ (фамилия, инициалы, подпись) Ростов-на-Дону 20__г.  УКАЗАНИЯ К ВЫПОЛНЕНИЮ курсовой РАБОТыСОДЕРЖАНИЕ РАБОТЫ (ПЕРЕЧЕНЬ, ПОДЛЕЖАЩИХ РАЗРАБОТКЕ ВОПРОСОВ) И ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЁТА 1 Теоретическая подготовка. 1.1Внутренние силовые факторы возникающие в поперечном сечении жёстко защемлённого стержня. 1.2Внутренние силы и напряжения при сдвиге. 1.3Внутренние силовые факторы возникающие в поперечном сечении двух опорной шарнирной балки. 2 Расчёт стержня на прочность . 2.1 Расчёт реакции в заделке. 2.2Построение эпюры продольных сил. 2.3Построение эпюры нормальных напряжений. 2.4Вывод о прочности стержня. Расчёт заклёпки на срез и смятие. 3.1Определение линий среза. 3.2Проверка прочности соединения на сдвиг (срез). 3.3Проверка прочности соединения на смятие. 3.4Вывод о прочности заклёпки. 4 Расчёт балки на изгиб. 4.1Определение реакций опор. 4.2Построение эпюры поперечных сил. 4.3Построение эпюры изгибающего момента. Заключение. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА III. Литература Основная: 1. Тарг, С.М. Краткий курс теоретической механики : Учебник для втузов / С. М. Тарг. - 20-е изд., стер. - М. : Высш. шк., 2010. - 416с. 2. Вереина Л.И. Техническая механика : Учебник для профтехобра-зования / Л. И. Вереина. - 4-е изд.,стер. - М. : Академия, 2007. - 224с. - (Начальное профессиональное образование). Дополнительная: 1. Александров, А.В. Сопротивление материалов : Учебник для вузов / А. В. Александров, В. Д. Потапов, Б. Д. Державин ; Под. ред. А.В. Александрова. - 4-е изд., испр. - М. : Высш. шк., 2004. - 560с. - 215-05. 2. Теория механизмов и детали машин. Под ред. В.Л. Воробьева. - М.,Воениздат,1985. 3. Курмаз Л.В. Детали машин. Проектирование : Сравочное учебно-метод. пособие / Л. В. Курмаз, А. Т. Скойбеда. - М. : Высш. шк., 2004. - 309с. «» 20__г. Подпись руководителя: ______________ « » 20__г. Задание принято к исполнению. Подпись курсанта: __________________  СОДЕРЖАНИЕ СОДЕРЖАНИЕ1 Введение…………………………………………………………………..5 2 Теоретическая подготовка……………………………………………..6 3 Расчёт стержня на прочность……………………………………….....20 4 Расчет заклепки на срез и смятие…………………………………… 22 5 Расчет балки на изгиб…………………………………………………. 23 6 Заключение…………………………………………………………….... 25 7 Список используемой литературы……………………………………26 8 Приложение №1 9 Приложение №2 Введение Курсовой проект по технической механике представляет собой одну из наиболее важных частей подготовки специалиста в области машиностроения, которое является основой технического перевооружения всех отраслей народного хозяйства. В настоящее время трудно представить себе промышленные предприятия без наличия тех или иных видов машин. Насыщенность производства средствами механизации трудоемких и тяжелых работ, уровень совершенства технологического процесса определяют собой степень совершенства технологического процесса и производительность предприятия. Современные высокоэффективные машины обеспечивают многократное повышение производительности труда человека. Дальнейшее развитие всех отраслей народного хозяйства, повышение роли науки и техники предъявляют все более высокие требования к качеству подготовки инженерных кадров. Специалисты, выпускаемые высшей школой, должны самостоятельно и творчески решать выдвигаемые научно-техническим прогрессом производственные вопросы, выполнять требования контрактов с зарубежными партнерами. Курсовое проектирование способствует закреплению, углублению и обобщению знаний, полученных курсантами за время обучения, и применение этих знаний к комплексному решению конкретной инженерной задачи. Системой курсовых проектов курсант подготавливается к выполнению более сложной инженерной задачи – дипломного проектирования. Наряду с этим курсовое проектирование учит пользоваться справочной литературой, а также прививает навыки выполнения расчетов, составление пояснительных записок. Выполняя свое задание, студент должен изучить существующие конструкции, обсудить с преподавателем все неясные и затруднительные места проекта и только после этого придать отдельным элементам законченную форму.  2.Теоретическая подготовка 2.1Внутренние силовые факторы возникающие в поперечном сечении жёстко защемлённого стержня Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю. Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений. Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на (рис. 1) 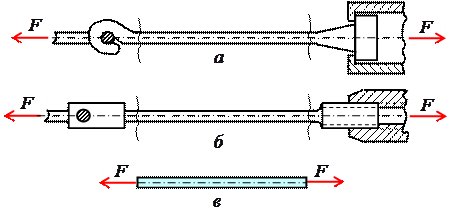 Рис. 1 Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис.1 а, б) оказывается единой (рис.1 в) согласно принципу Сен – Венана. Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2 б). Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2 б), а при сжатии – к сечению.  Рис. 2   Растягивающие продольные силы принято считать положительными (рис.3а), а сжимающие – отрицательными (рис. 3 б). 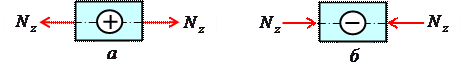 Рис. 3 Вместе с тем между растяжением и сжатием могут обнаружиться и качественные различия, как, например, при изучении процессов разрушения материала или при исследовании поведения длинных и тонких стержней, для которых сжатие сопровождается, как правило, изгибом. При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки. Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений. График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы. Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня. Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие принято называть опасным. Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня. Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.  2.2Внутренние силы и напряжения при сдвиге. Одним из распространённых форм деформации является сдвиг отдельных слоёв изделия в вертикальной или горизонтальной плоскости. Такое смещение называется – деформация сдвига. Изменение положения может вызывать постепенное или резкое изменение первоначальной формы конструкции или отдельной детали. Виды деформации характеризуют порядок произведенного смещения и определяют порядок расчёта основных характеристик. В технической механике и сопромате рассматривают два вида деформации со сдвигом: плавное (смятие) и резкое (разрыв или срез). 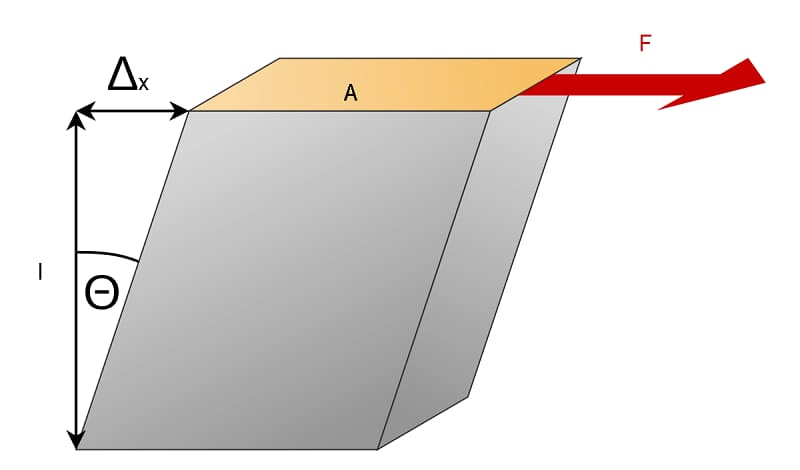 Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным. Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся: при распиловке бруса; отрезание или рубка металла; в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами; балки в местах крепления опор; места скрепления мостовых пролётов; крепёж на перемычках соединения железнодорожных рельс; разрезания листа бумаги ножницами. При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.  2.3Внутренние силовые факторы возникающие в поперечном сечении двух опорной шарнирной балки. Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.4 а). В этой же плоскости располагается изогнутая ось стержня (упругая линия) (рис. 4 б). Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.4). 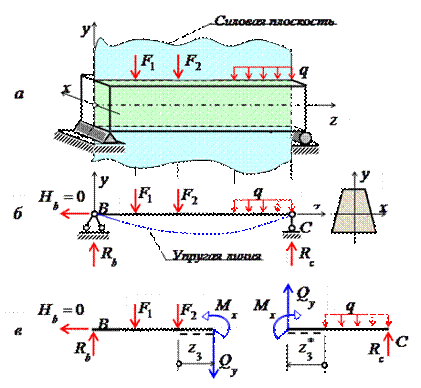 Рис.4 При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.4,в): поперечная сила Qy , где y – ось симметрии (главная центральная ось) и изгибающий момент Mx. , где x – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M. Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.5). При наличии поперечной силы Qy изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь. Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.  Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях. Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.  Рис.5 3.Расчёт стержня на прочность Построить эпюры: продольной силы N и нормальных напряжений σ. При F1 =8кН,F2 =5кН, A1=4 см2 , A2=2 см2, σдоп=32МПа. 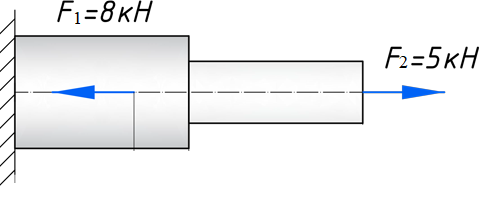 3.1 Расчёт реакции в заделке. Для того чтобы рассчитать реакцию в заделке необходимо стержень привезти в состояние равновесия. Следовательно реакция в заделке R=3кН и направлена в право. 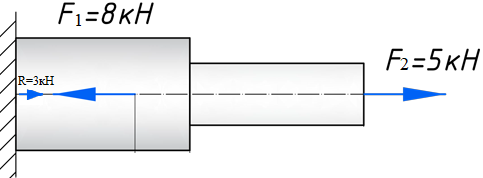 3.2Построение эпюры продольных сил Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, на которых эта эпюра будет иметь постоянное значение. Конкретно, для продольной эпюры, границами участков служат те точки, где прикладываются силы. Для данного примера, нужно рассмотреть всего 2 участка: 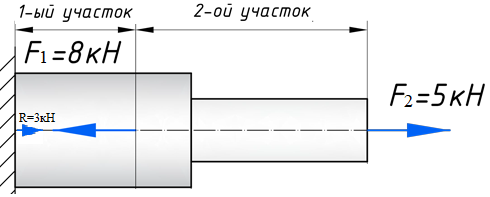   На первом участке реакция в заделке R растягивает брус на величину 3кН N1 = R=-3кН 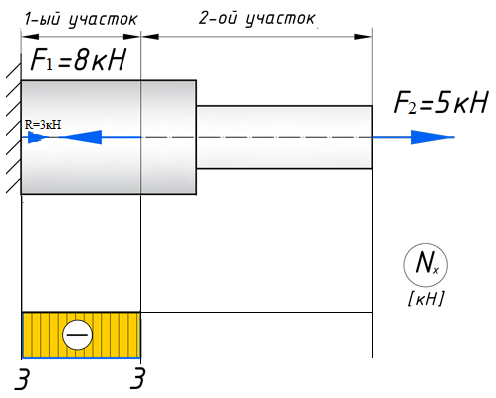 На втором участке сила F=8кН , поэтому на этом участке, продольная сила будет положительнойи равной: N2 = = R+ N1=5кН Откладываем это значение на графике. Эпюры в сопромате, принято штриховать перпендикулярно нулевой линии, а также для продольных сил, на эпюрах проставляются знаки: 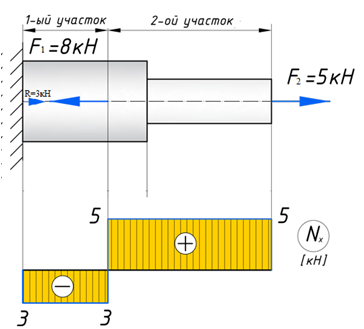   3.3Построение эпюры нормальных напряжений В отличие от продольных сил, нормальные напряжения зависят от площади поперечных сечений бруса и вычисляются , по следующей формуле: 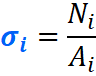 Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для данного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза: 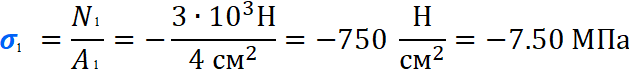 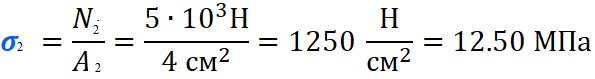 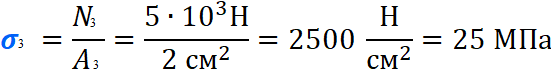  По полученным значениям строим эпюру нормальных напряжений: 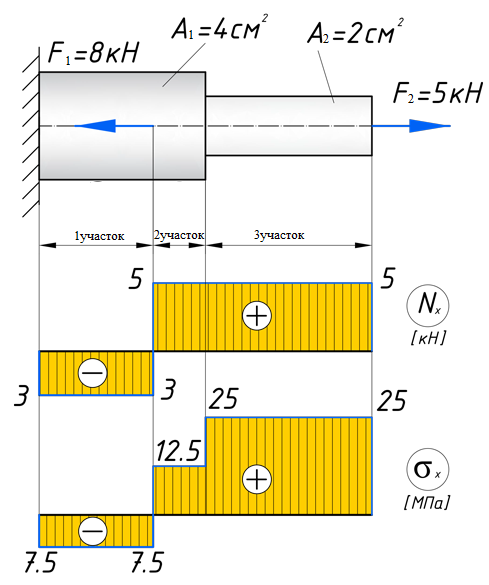 3.4Вывод о прочности стержня На основе произведённых расчётов, сравнив максимальное напряжение с допустимым, можно сделать вывод о прочности стержня σдоп=32МПа, σmax=25МПа σдоп>σmax Следовательно прочность стержня обеспечена  Расчёт заклёпки на срез и смятие  Проверить прочность заклепочного соединения на срез и смятие. Нагрузка на соединение 60 кН, [τс] = 100 МПа; [σсм] = 240 МПа. 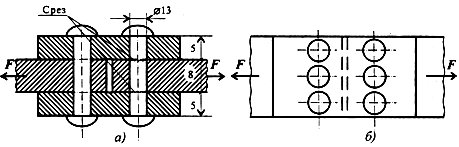 4.1Определение линий среза Соединение двухсрезными заклепками последовательно воспринимается тремя заклепками в левом ряду, а затем тремя заклепками в правом ряду. Площадь сдвига каждой заклепки Ас = 2πr2. Площадь смятия боковой поверхности Aсм = dδmin. 4.2 Проверим прочность соединения на сдвиг (срез). Q = F/z — поперечная сила в поперечном сечении заклепки: Прочность на сдвиг обеспечена. Проверим прочность соединения на смятие: 4.4 На основании произведённых расчётов можно сделать вывод о прочности заклёпки. Прочность заклепочного соединения обеспечена.  5 Расчёт балки на изгиб Для заданной двухопорной шарнирной балки нагруженной моментом построить эпюры Q и M если Мизг=5Нм, a=3м, b=2м. 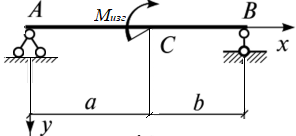 5.1Определение реакций опор Задаём направление реакций в опорах  Записываем уравнения равновесия ∑Fx = 0,=>RAX=0. ∑Fy = 0, ∑MАВ= 0; -5+5RBY=0 RBY=1H 5RAY-5=0 RAY=1H Проверка: -1+1=0=> реакции в опорах рассчитаны верно. 5.2Построение эпюры поперечных сил Из условия известно, что на балку действует только 2 силы они же реакции опор, зная это, делаем два сечения в начале и в конце балки. Рассчитываем в этих сечениях значения поперечных сил. Q1=-1H Q2=-1H Строим эпюру поперечных сил.  5.3Построение эпюры изгибающего момента Для построения эпюры изгибающего момента необходимо сделать четыре сечения и рассчитать значение изгибающего момента в каждом сечении. М1=0 т.к. у реакции опоры RAY нет плеча. М2=-1*3=-3Нм М3=-1*3+5=2Нм М4=0 т.к. у реакции опоры RBY нет плеча. Строим эпюру изгибающего момента.     3. Расчёт стержня на прочность П  острою эпюры: продольных сил N и нормальных напряжений σ. При острою эпюры: продольных сил N и нормальных напряжений σ. При  . . Р  ассчитываем значение и задаём направление реакции заделки. ассчитываем значение и задаём направление реакции заделки.Рассчитываем значение продольных сил:   ; ;N3 = 0кН Рассчитываем значение нормальных напряжений: 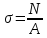 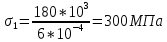 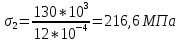 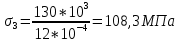 Следовательно, прочность стрежня необеспеченна. Рассчитываем значение удлинение на каждом участке: 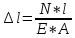 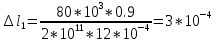 м м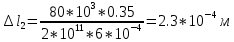 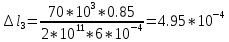 м мРассчитываем значение перемещения: 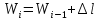 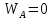 м м  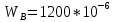 м м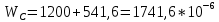 м м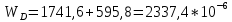 м мРассчитываем значение работы на каждом участке: 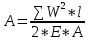 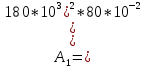 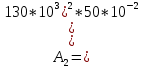 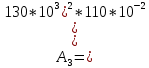 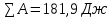 Графическую часть смотреть в приложении №1 Ответ: На основе произведённых расчётов, сравнив максимальное напряжение с допустимыми, можно сделать вывод о прочности стержня. 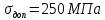 < <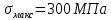 . .  4.Расчёт заклёпки на срез и смятие 4.Расчёт заклёпки на срез и смятиеПроверим прочность заклёпочного соединения на срез и смятие. Дана нагрузка на соединение:  Расчёт заклёпки на срез и смятие:  Рассчитываем напряжение в заклёпке на срез:   Рассчитываем напряжение в заклёпке на смятие: 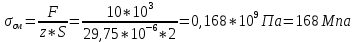 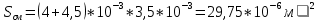 Ответ: На основе произведённых расчётов можно сделать вывод о прочности заклёпки. Прочность заклёпочного соединения на срез и смятие необеспеченна.  5. Расчёт балки на изгиб 5. Расчёт балки на изгибД 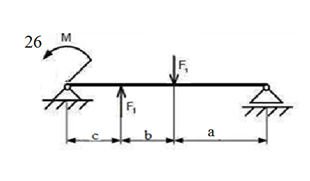 ля заданной двух опорной шарнирной балки нагруженной моментом построил эпюры Q И M . ля заданной двух опорной шарнирной балки нагруженной моментом построил эпюры Q И M .Дано: a=3(м); b=1(м); c=1(м); M=30(кНм); F1=4(кН) Записываем уравнение равновесия: 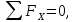 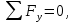 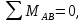 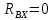 Р 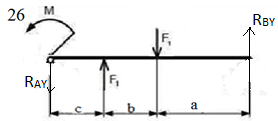 асставляем реакции в опорах: асставляем реакции в опорах: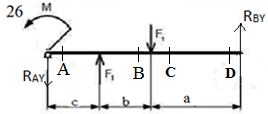 Составляем уравнение моментов относительно точке А: 30-40*4+40*3-5RAY=0 5RAY=-10 RAY=-2 Составляем уравнение моментов относительно точке B: 30+40-40*2+5RBY=0 5RBY=10 RBY=-2 Проверяем правильность нахождения значений реакций в опорах: П:-2-40+40+2=0 т.к. в результате получился ноль, следовательно реакция опоры найдена верно. Рассчитываем значения поперечных сил в каждом сечении: Q1=-2H; Q2=-2+40=38H; Q3=-2+40-40=-2H; Q4=-2+40-40=-2H. Рассчитываем значение изгибающего момента в каждом сечении: 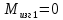 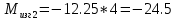 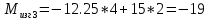 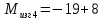 =-11 =-11Графическую часть смотреть в приложении №2 Ответ: На основе произведённых расчётов построили эпюру поперечных сил и изгибающего момента. Прочность заклёпочного соединения на срез и смятие обеспеченна.  6. Заключение В данной курсовой работе я, курсант Шелуха Александр Александрович закрепил, углубил и обобщил знания, полученные за время обучения, и применил эти знания к комплексному решению конкретных задач. Пользуясь справочной литературой и законспектированными лекциями. В первой задаче расчётной части Выполнил расчёт реакции в заделке стержня, построил эпюры продольных сил и нормальных напряжений, а также сделал вывод о прочности стержня. Значение продольных си и нормальных напряжений, удлинение стержня по действиям этих сил и перемещение поперечных сечений на каждом участке. Во второй задаче расчётной части выполнил расчёт заклёпки на прочность, рассчитав фактические напряжения на срез и смятие, и дал оценку прочности стержня, сравнив их с максимально допустимыми напряжениями. Рассчитал балку на изгиб, определил реакцию опоры, построил эпюры поперечных сил и изгибающего момента. В третьей задаче расчётной части рассчитал значение реакций в шарнирных опорах, сделал расчёт поперечных сил и сгибающего момента в каждом сечении. Все расчёты отображены на графиках в приложениях 1 и 2.  7.Список использованной литературы Основная: 1. Тарг, С.М. Краткий курс теоретической механики : Учебник для втузов / С. М. Тарг. - 20-е изд., стер. - М. : Высш. шк., 2010. - 416с. 2. Вереина Л.И. Техническая механика : Учебник для профтехобра-зования / Л. И. Вереина. - 4-е изд.,стер. - М. : Академия, 2007. - 224с. - (Начальное профессиональное образование). Дополнительная: 1. Александров, А.В. Сопротивление материалов : Учебник для вузов / А. В. Александров, В. Д. Потапов, Б. Д. Державин ; Под. ред. А.В. Александрова. - 4-е изд., испр. - М. : Высш. шк., 2004. - 560с. - 215-05. 2. Теория механизмов и детали машин. Под ред. В.Л. Воробьева. - М.,Воениздат,1985.  3. Курмаз Л.В. Детали машин. Проектирование : Сравочное учебно-метод. пособие / Л. В. Курмаз, А. Т. Скойбеда. - М. : Высш. шк., 2004. - 309с. 3. Курмаз Л.В. Детали машин. Проектирование : Сравочное учебно-метод. пособие / Л. В. Курмаз, А. Т. Скойбеда. - М. : Высш. шк., 2004. - 309с. |
