Смежные углы

• Название: Смежные углы
• Дата: 06.05.2022
• Размер: 1.61 Mb.
• Имя файла: 066192223ea80ad8a752f3ae2d9a3427.doc
• Тип: Задача; #515501
• страница: 3 из 4

1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство:Пусть прямая a || b и прямая с пересекает прямую а в точке М.Докажем, что тогда прямая с пересекает и прямую b. Если бы прямая с не пересекала прямую b, то через точку М проходили бы 2 прямые (а и с) параллельные прямой b. Но это противоречит аксиоме параллельных прямых, значит прямая с пересекает прямую b.
2) Если две различные прямые параллельны третьей прямой, то они параллельны.

2. 
   (п. 34) Свойства прямоугольных треугольников:
   

1⁰. Сумма двух острых углов в прямоугольном треугольнике равна 90⁰.
Доказательство:В самом деле,сумма углов треугольника равна180⁰,а т.к.прямой угол= 90⁰,тосумма двух других углов в треугольнике = 90⁰.
2⁰. Катет прямоугольного треугольника, лежащий против угла в 30⁰, равен половине гипотенузы.
Доказательство:Пусть в прямоугольном∆АСВ∠В=30°.Тогда другойего острый угол будет равен 60°. Докажем, что катет АС равен половине гипотенузы АВ.
Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник – равносторонний. Катет АС равен половине AM, а так как AM равняется АВ, то катет АС будет равен половине гипотенузы АВ. Ч.т.д.
3⁰. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30⁰.
3. Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.
Доказательство:

Билет. 11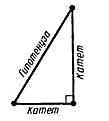

1. 
   (п. 31) Прямоугольный треугольник – это треугольник, у которого один угол прямой, т.е. равен 90⁰. Сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны - катетами. Гипотенуза всегда большего любого из катетов, т.к. лежит напротив большего угла в треугольнике.
   

2. 
   (п.29) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
   

Дано: а||b, с –секущая,

Д 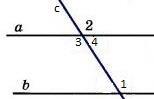оказать,что соответственные углы∠1 =∠2.
Доказательство:т.к. а||b,то∠1 =∠3 (накрест лежащие),а∠3 =∠2(вертикальные), следовательно ∠1 = ∠2. Ч.т.д.
3. Найти смежные углы, если один из них на 45⁰ больше другого.

	Решение: Обозначим ∠2 = х, тогда ∠1 = х + 450.
∠1	По свойству смежных углов ∠1 + ∠2 = 1800.
∠2	Составим уравнение х + х + 450 = 1800; 2х = 1350; х = 1350 : 2 = 67,50.
	Значит ∠2 = 67,50, тогда ∠1 = 67,50 + 450 = 112,50.

О твет: ∠1 = 112,5⁰; ∠2 = 67,5⁰.
Билет. 12

1. (п. 11) Смежные углы – это два угла, у которых одна сторона общая,	∠1
а две другие являются продолжениями одна другой.	∠2

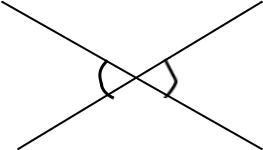
Свойство: Сумма смежных углов равна 180⁰.

На рисунке ∠1 и ∠2 вместе образуют развернутый угол, а он равен 180⁰, следовательно, ∠1 + ∠2 = 180⁰.

2. 
   (п.35) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
   

Дано:∆АВС и∆А₁В₁С₁–прямоугольные,АВ=А₁В₁и СВ=С₁В₁,углы С и С₁ – прямые.
Доказать,что∆АВС= ∆А₁В₁С₁Доказательство:т.к.∠С=∠С₁= 90⁰,то∆АВС можно наложить на
∆А₁В₁С₁ так, что вершина С совместится с С₁, а стороны СА и СВ наложатся на лучи С₁А₁ и С₁В₁. По условию СВ = С₁В₁, значит, вершина В совместится с В₁. Но тогда и вершина А совместится с А_1.
Ч.т.д.

2. 
   Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.
   

Дано:В∆АВС биссектриса ВД–это высота.Доказать,что∆АВС равнобедренный.Доказательство: ∆АВД= ∆СВД по второму признаку
(∠1 =∠2, т.к. ВД – биссек., ∠3 =∠4=90⁰, т.к. ВД – высота, а сторона ВД – общая).

З 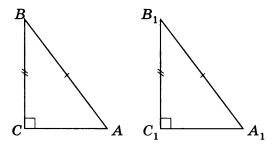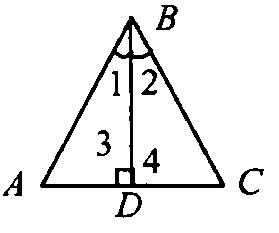начит АВ = ВС, т.е. ΔABC – равнобедренный. Ч.т.д.
Билет. 13

1. (п. 11) Вертикальные углы – это два угла, у которых		стороны одного угла	являются
продолжениями сторон другого.
Теорема: Вертикальные углы равны.			2
Доказательство: ∠1 + ∠2 = 1800 (смежные),		1	3
∠3 + ∠2 = 1800 (смежные),	→ ∠1 = ∠3. Ч.т.д.

2. (п.35) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Дано: ∆АВС и∆А₁В₁С₁–прямоугольные,АВ=А₁В₁,∠С=∠С₁= 90⁰,∠В=∠В₁.Доказать,что∆АВС= ∆А₁В₁С₁
Доказательство:т.к.∠С=∠С₁= 90⁰и∠В=∠В₁,следовательно,∠А=∠А₁(по теореме о сумме углов втреугольнике), а значит ∆АВС равен ∆А₁В₁С₁ по второму признаку равенства треугольников (у них равны гипотенуза и два прилежащих к ней угла)_. Ч.т.д.
3. Отрезки АВ и СЕ пересекаются в их общей середине О. На отрезках АС и ВЕ отмечены точки К и М так, что АК = ВМ. Доказать, что ОК = ОМ.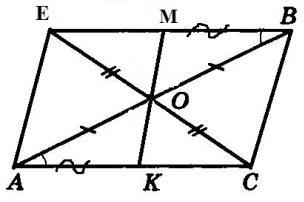




Доказательство:Соединим точки А,С,В,Е.Получиличетырёхугольник, диагонали которого делятся точкой пересечения пополам. А, значит, этот четырёхугольник – параллелограмм. ЕС и АВ – диагонали параллелограмма АСВЕ. ∠ОАС = ∠ОВЕ (как накрест лежащие при параллельных прямых АС и ВЕ и секущей АВ). Получили, что ∆АОК = ∆ВОМ по первому признаку равенства треугольников (АО = ОВ, АК = МВ, ∠ОАС = ∠ОВЕ). В равных треугольниках оставшиеся стороны равны, т.е. ОК = ОМ. Ч.т.д.
Билет. 14

1. 
   Отложить на данном луче от его начала отрезок, равный данному. Смотри презентацию, слайд 2.
   

2. 
   (п.18) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
   

Дано: ∆АВС,АВ=ВС,ВО–биссектриса.Доказать,что ВО–медиана и высота.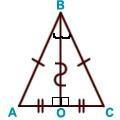




Доказательство: Рассмотрим ∆ABO и ∆CBO. У них:
AB = BC (по условию), BO – общая сторона, ∠AВO = ∠СВО (т.к. BO – биссектриса). Значит эти треугольники равны по 1 признаку. Следовательно, AO = OС, а значит BO – медиана.
Далее, ∠AOC – развернутый угол = 180°. Но т.к. ∆ABO = ∆CBO, то ∠AOB = ∠COB = 180°/2 = 90⁰, значит BO – высота. Ч.т.д.
3. Один из углов прямоугольного треугольника равен 60⁰, а сумма гипотенузы и меньшего из катетов равна 26,4см. Найдите гипотенузу треугольника.
Решение:Пусть в данном треугольнике∠В= 90⁰,∠A = 60⁰.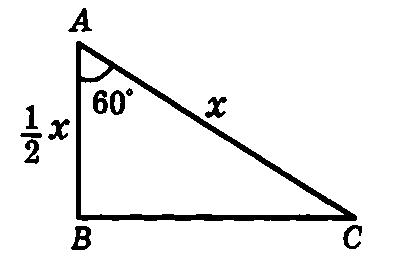




Тогда ∠С = 180⁰ – 90⁰ – 60⁰ = 30⁰. Меньший из катетов лежит напротив угла в 30⁰ и, значит, равен половине гипотенузы (по 2 свойству). Обозначим
гипотенузу АС = х, тогда катет АВ = ½*х. Составляем уравнение: х + ¹₂ х = 26,4 (по условию). Отсюда ³₂ х = 26,4 или х = 17,6. Ответ: гипотенуза АС = 17,6см.




Билет. 15

1. 
   (п.29) Во всякой теореме есть 2 части: условие и заключение. Условие теоремы – это то, что дано, а заключение – то, что требуется доказать.
   

Например, рассмотрим теорему: Если 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника, то такие треугольники равны. В ней условием будет утверждение: 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника (это дано), а
заключение: треугольники равны (это требуется доказать).
Теоремой, обратной данной, называется такая теорема, в которой условие и заключение меняются местами.
Например, для данной выше теоремы обратной теоремой будет: Если треугольники равны, то у них все стороны соответственно равны.
Или для теоремы: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Обратная теорема будет звучать так: Если две параллельные прямые пересечены секущей, то соответственные углы равны.

2. 
   (п.28) Если две прямые параллельны третьей прямой, то они параллельны.
   

Доказательство:Действительно,пусть а ||с и b ||с.Докажем, что тогда а || b.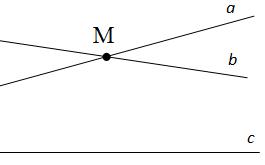




Допустим, что прямые а и b не параллельны, т.е. пересекаются в какой-то точке М. Тогда получим, что через точку М проходят 2 прямые (а и b) параллельные прямой с, а это противоречит аксиоме параллельных прямых. Поэтому наше предположение было неверным, а значит, прямые а и b параллельны.
3. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50⁰. Найти эти углы.

Р 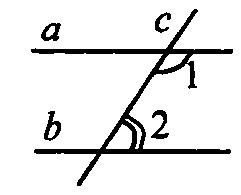ешение:Т.к.а||b,∠1 +∠2 = 180⁰.Пусть∠1 =х,тогда∠2 =х–50.

Составляем уравнение: х + х – 50 = 180. 2х = 230, х = 115,

т.е. ∠1 = 115⁰, ∠2 = 55⁰.
Билет. 16

1. 
   Как построить треугольник по стороне и двум прилежащим к ней углам. Смотри презентацию,
   

слайд 9.

2. 
   (п.30) Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
   

Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: ∆АВС,∠4–внешний.

Доказать,что∠4 =∠1 +∠3.

Доказательство: ∠1 + ∠3 + ∠2 = 180⁰ (по теореме о сумме углов ∆).

∠4 + ∠2 = 180⁰ (смежные)

Следовательно, ∠4 = ∠1 + ∠3. Ч.т.д.
3. Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой. Дано:О–середина АВ, l –прямая,проходящая через О.

Д 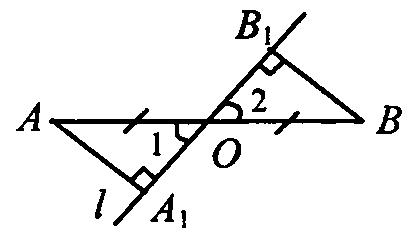оказать,что АА₁=ВВ₁.
Доказательство:АА₁ l иВВ₁ l.Рассмотрим прямоугольныетреугольники АОА₁ и ВОВ₁. Они равны по гипотенузе и острому углу (АО = ОВ по условию, ∠1 =∠2, как вертикальные).
Следовательно, АА₁ = ВВ₁. Ч.т.д.
Билет. 17

1. 
   (п.24, 37) Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: а ǀǀ b.
   

Два отрезка называются параллельными, если они лежат на параллельных прямых.
Расстоянием от точки до прямой называется длина перпендикуляра,проведенного из этой точки кпрямой.
Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной изпараллельных прямых до другой прямой.

2. 
   (п.32) В треугольнике против большего угла лежит большая сторона.
   

Д ано: ∆АВС,∠С>∠В.

Доказать,что АВ>АС.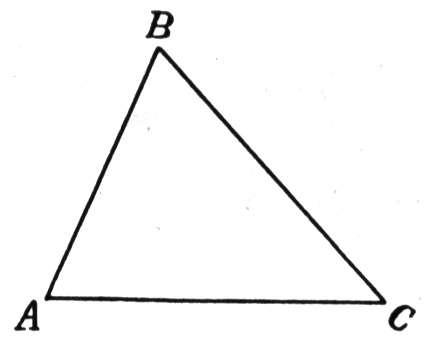




Доказательство:Предположим,что это не так.
Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆АВС
– равнобедренный, а значит углы при основании равны, т.е. ∠С=∠В, а это противоречит условию, что ∠С > ∠В. Во втором случае получаем, что ∠С < ∠В (т.к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше предположение неверно, и, следовательно, АВ > АС. Ч.т.д.
3. В ∆АВС ∠А = 40⁰, а ∠ВСЕ смежный с ∠АСВ равен 80⁰. Доказать, что биссектриса ∠ВСЕ параллельна прямой АВ.

Д ано:∠А= 40⁰,а∠ВСЕ= 80⁰,СК–биссектриса∠ВСЕ.

Доказать,СКǀǀАВ.
Доказательство:∠ВСК=∠КСЕ=½∠ВСЕ= 80⁰/2 = 40⁰.
Получили, что ∠ВАС = ∠КСЕ = 40⁰, а это соответственные углы при прямых АВ, СК и секущей АС. Раз они равны, то СК ǀǀ АВ. Ч.т.д.