Смежные углы

• Название: Смежные углы
• Дата: 06.05.2022
• Размер: 1.61 Mb.
• Имя файла: 066192223ea80ad8a752f3ae2d9a3427.doc
• Тип: Задача; #515501
• страница: 1 из 4

Экзаменационные билеты по геометрии. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы». Найдите величины смежных углов, если один из них в 5 раз больше другого.
Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников». Отрезки AC и BM пересекаются и точкой пересечения делятся пополам. Доказать, что треугольник ABC равен треугольнику CMA.
Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность». На окружности с центром О отмечены точки А и В так, что угол AOB прямой. Отрезок ВС - диаметр окружности. Докажите, что хорды AB и AC , равны.
Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

2. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Внешний угол треугольника». Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.
Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники». В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.
Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых». Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.
Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезок АМ-биссектриса треугольника ABC. Через точку M проведена прямая, параллельная AC и пересекающая сторону AB в точке E. Доказать, что треугольник AME равнобедренный.
Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников». На биссектрисе угла А взята точка E, а на сторонах этого угла точки В и С такие, что угол AEC равен углу AEB. Доказать, что BE равно CE.
Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезки AB и CD пересекаются в их общей середине. Доказать, что прямые AC и BD параллельны.
Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Соотношения между сторонами и углами треугольника».

Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы». Найти смежные углы, если один из них на 45 больше другого.
Билет №12.

1. Смежные углы ( определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

3. Задача на тему «Свойства равнобедренного треугольника».

Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.
Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников». Отрезки AB и CE пересекаются в их общей середине О. На отрезках AC и BE отмечены точки К и M так, что AK равно BM. Доказать, что OK равно OM.
Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников». Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.
Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых». Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50. Найти эти углы.
Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

3. Задача на тему «Расстояние от точки до прямой».

Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой.
Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Признаки параллельности двух прямых». В треугольнике ABC угол А равен 40, а угол ВСЕ, смежный с углом ACB, равен 80.Доказать, что биссектриса угла ВСЕ параллельна прямой AB.
Билет №18.

1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой». В равнобедренном треугольнике ABC с основанием АС = 37 см, внешний угол при вершине В равен 60. Найти расстояние от вершины С до прямой AB.
Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника». Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найти боковую сторону данного треугольника.
Билет №20.

1. Объясните, как построить биссектрису данного угла.

2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников». В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС + АВ = 18 см. Найти AC и AB.

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E. Доказать, что треугольник АСО равен треугольнику MEH.
Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°
Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и  OKM = 96°.
Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Неравенство треугольника».

В равнобедренном треугольнике одна сторона равна 25см, а другая равна 10 см. Какая из них является основанием?
Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Прямые АВ и CD пересекаются в точке О. Угол АОС равен 58⁰. Найдите угол ВОD.

Билет. 1

1. (п.1) К основным геометрическим фигурам на плоскости относятся точка и прямая линия.
Точка —это самая малаягеометрическая фигура,которая является основой всех прочих построений(фигур).
Прямую линию,или прямую,можно представить себе как бесчисленное множествоточек,которыерасположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:




Часть прямой линии, ограниченная с двух сторон точками, называется отрезком.
Отрезок изображается так: Длина отрезка - положительное число, показывающее, сколько раз единичный отрезок и его части
укладываются в данном отрезке. Длину отрезка АВ также называют расстоянием между точками А и В. Свойства:

1. 
   Длины равных отрезков равны;
   
2. 
   Длина суммы отрезков равны сумме их длин.
   

Обычно прямые обозначаются малыми латинскими буквами a, b, c, d, а точки – большими A, B, C...
Через любые 2 точки можно провести прямую и притом только одну.
Любые 2 прямые на плоскости либо имеют одну общую точку (пересекаются), либо не имеют общих точек (параллельны).
2. (п.20) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.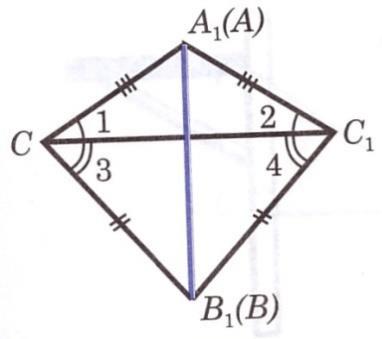




Дано: ∆АВС и∆А₁В₁С₁,у них АВ=А₁В₁,АС=А₁С₁,ВС=В₁С₁.Доказать,что∆АВС= ∆А₁В₁С₁
Доказательство:Приложим∆АВС к∆А₁В₁С₁так,чтобы сторона АВ совпала со стороной А₁В₁, а точки С и С₁ оказались по разные стороны от АВ.
По условию АС=А₁С₁, ВС=В₁С₁ → ∆А₁С₁С и ∆В₁С₁С – равнобедренные, а значит ∠1 = ∠2, ∠3 = ∠4 (углы при основании), поэтому весь ∠А₁СВ₁ = ∠А₁С₁В₁.

Итак, мы получили, что АС=А₁С₁, ВС=В₁С₁, ∠С = ∠С₁, следовательно ∆АВС = ∆А₁В₁С₁
(по I признаку). Ч.т.д. 3. Найдите величины смежных углов, если один в 5 раз больше другого.

Решение: Обозначим один из углов х, другой значит будет 5х, т.к. он в 5 раз больше.
Сумма смежных углов всегда 180⁰, получаем уравнение х + 5х = 180⁰, откуда 6х = 180⁰, х = 30⁰. Значит один из смежных углов 30⁰, другой 30*5 = 150⁰.
Билет. 2
1. (п. 14) Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его
сторонами. Виды треугольников:




2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Д 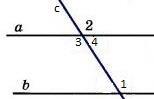ано:прямые а и b, с –секущая,соответственные углы∠1 =∠2.

Доказать,что а||b
Доказательство:∠1 =∠2 (по условию),∠2 =∠3 (вертикальные),следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b.
Ч.т.д.

3. Отрезки АС и ВМ пересекаются в точке О и делятся ею пополам. Докажите, что ∆АВС = ∆СМА.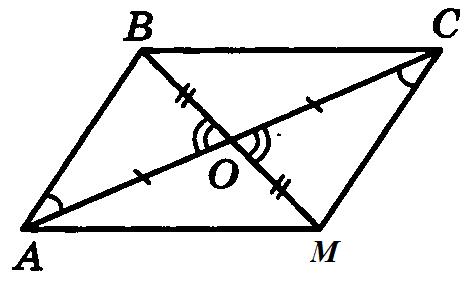




Дано:АО=ОС и ВО=ОМ.Доказать,что∆АВС= ∆СМА
Доказательство:Пусть отрезки АС и ВМ пересекаются в точке О.Тогда ∆АОВ = ∆СОМ по I признаку (АО = ОС и ВО = ОМ по условию, а ∠АОВ = ∠СОМ как вертикальные). Следовательно, ∠ВАО = ∠МСО и сторона АВ = МС (в равных треугольниках против равных углов лежат равные стороны).

Тогда ∆АВС = ∆СМА тоже по I признаку (∠ВАО = ∠МСО, АВ = МС, АС – общая сторона). Ч.т.д.
Билет. 3

1. (п.17)
Медиана – это отрезок, идущий из вершины треугольника к середине противоположной стороны. (Нельзя говорить идущий в противоположную сторону…)




^А1
А
Биссектриса – это отрезок, идущий из вершины треугольника к противоположной стороне и
делящий угол треугольника пополам.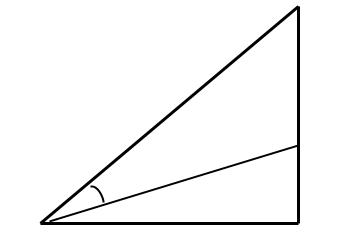


А₁

30⁰

• 
  30⁰
  

Высота – это перпендикуляр, идущий из вершины треугольника к противоположной стороне.
(Перпендикуляр – это отрезок, падающий под углом в 90⁰ к прямой).
Высота – это единственная линия в треугольнике, которая при построении может оказаться снаружи треугольника.
В любом треугольнике все 3 медианы пересекаются в одной точке, все 3 биссектрисы пересекаются в одной точке и все 3 высоты пересекаются в одной точке.

2. 
   (п.25) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
   

Дано:прямые а и b, АВ –секущая,накрест лежащие углы∠1 =∠2.

Доказать,что а||b
Доказательство: (метод от противного).Предположим,что прямые а и b не параллельны,а значит они пересекаются в некоторой точке М.Рассмотрим ∆АВМ: ∠1 будет внешним углом для этого треугольника, а ∠2 – внутренним. Из теоремы о внешнем угле треугольника следует, что ∠1 больше ∠2, а это противоречит условию (∠1 = ∠2), значит, прямые а и b не могут пересекаться, поэтому они параллельны. Ч.т.д.

2. 
   На окружности с центром О отмечены точки А и В так, что ∠АОВ – прямой. Отрезок ВС – диаметр окружности. Докажите, что хорды АВ и АС равны.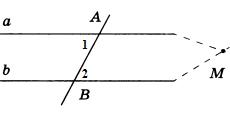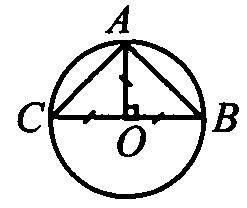
   

Доказательство:Рассмотрим∆ВОА и∆СОА,у них сторона ОА–общая,СО=ОВ(как радиусы одной окружности), ∠СОА = ∠ВОА = 90⁰.
Следовательно, ∆ВОА = ∆СОА по I признаку. А раз треугольники равны, то их соответственные стороны тоже равны, т.е. АВ = АС. Ч.т.д.

Билет. 4