Рациональное использование природных ресурсов. Содержание 1анализ и тенденции развития литья теплоэнергетического оборудования 5
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
5ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ5.1ОСНОВЫ ТЕРМОКИНЕТИЧЕСКОЙ ТЕОРИИ КРИСТАЛЛИЗАЦИИН.Г.Гиршович, Г.Ф.Баландин, Б.Я.Любов и Ю.А.Самойлович на основании синтеза теплофизической и молекулярно-кинетической теории создали математическую модель [35], позволяющую решить вопросы, связанные с особенностями формирования кристаллического строения слитков. Для сплава, кристаллизующегося в интервале температур ТL - ТS, залитого в форму при температуре ТН, в некоторый промежуточный момент затвердевания распределение температур представлено на Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1[34]. 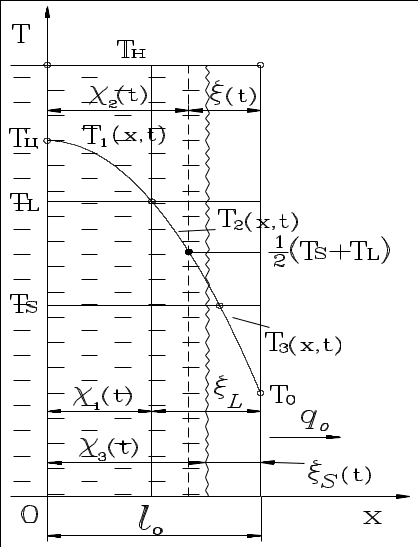 Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1. Схема температурных полей затвердевающей отливки Процесс затвердевания развивается в двухфазной зоне расплава, прилегающей к твердой корке. На Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1представлена схема температурных полей: Т1(x,t) - температурное поле в незатвердевшем расплаве, Т2(x,t) - в двухфазной зоне и Т3(x,t) - в твердой корке; c1(t) и c3(t) - соответственно координаты фронтов начала и конца затвердевания. Если внутри интервала кристаллизации сплава выбрать температуру, равную, например, 1/2×(ТL + TS ), и принять, что к моменту ее достижения в двухфазной зоне практически заканчивается процесс кристаллизации (Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1), то кинетику затвердевания можно характеризовать скоростью нарастания твердой корки x(t). Для математического описания такого варианта схемы можно использовать все уравнения и соотношения, которые были получены Г.Ф.Баландиным [34] применительно к схеме затвердевания металлов и эвтектик. Необходимо лишь вместо c3(t) подставить координату c2(t) условного фронта затвердевания (Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1) и Ткр заменить 1/2×(ТL + TS): 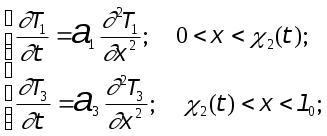 (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-1) (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) 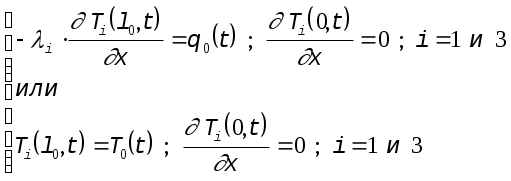 (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) 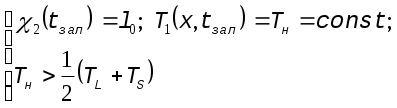 (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) Несмотря на очень грубую схематизацию процесса затвердевания, с помощью рассмотренного способа математического описания можно достаточно просто, но, естественно, приближенно рассчитать линейную скорость затвердевания U, которая необходима для практического применения экспериментальных данных и диаграмм, устанавливающих связь свойств и структуры отливки со скоростью ее затвердевания [34]. Данная математическая модель справедлива для отливки в виде неограниченной плиты. Правомерно ли ее использование в данном случае ? 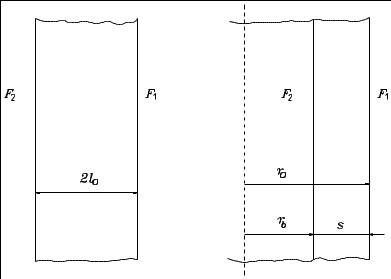 Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-2. Схемы для сравнения плоской и полой цилиндрической отливки Сравним плоскую отливку (плиту) с простейшим полым бесконечным цилиндром (Рис.ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-2), т.к. в нашем случае основной элемент конструкции отливки теплообменник - труба, т.е. полый цилиндр. Известно, что все поверхности, ограничивающие плиту, имеют радиус кривизны, равный бесконечной величине. Поэтому, если радиус кривизны боковых поверхностей плиты обозначить через r0, то отношение 2l0/r0 = 0. Следовательно, любую неплоскую отливку, у которой отношение толщины s ее тела к радиусу кривизны r0 ее поверхности будет весьма малой величиной, можно приближенно рассматривать как плоскую, т.е. если (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) то отливка плоская. Еще одно очевидное свойство плоской отливки в том, что у нее обе боковые поверхности F1 и F2 равны друг другу. Поэтому любую неплоскую отливку, у которой отношение (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) можно приближенно рассматривать как плоскую. Неравенство (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) и выражение (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) связаны между собой. Так, для полого цилиндра (втулки) (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) Допустим, что при приближенных расчетах затвердевания возможно пренебречь разницей, составляющей 20 %, между площадями наружной F1 и внутренней F2 поверхностей тела отливки. Другими словами, примем, что при F2/F1 = 0.8 величина F1 » F2. Тогда для полого цилиндра s/r0 = 0.2. Следовательно, можно условиться, что при [34] (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) отливки тонкостенные, и в расчетах затвердевания они являются плоскими. Анализ номенклатуры литых деталей машиностроения и приборостроения показывает, что подавляющее большинство отливок удовлетворяет требованию (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-); это - корпусные детали, детали арматуры, кронштейны, станины и т. п. Правда, соответствие требованию (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) нельзя понимать в буквальном смысле. На таких деталях, конечно, есть бобышки, приливы, утолщения, ребра и другие элементы, толщина которых отличается от толщины основного тела. Говоря о соответствии требованию (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) имеем в виду толщину и радиусы кривизны поверхности основного тела (или среднюю толщину тела и средний радиус кривизны для детали в целом) [34]. Отливка теплообменник удовлетворяет этим условиям, т.к. s = 8 мм, r0= 38 мм, (ПОСТРОЕНИЕ ПРИБЛИЖЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СКОРОСТИ ЗАТВЕРДЕВАНИЯ ОТЛИВКИ-) Следовательно, данная математическая модель справедлива для расчетов затвердевания отливки теплообменник. |
