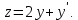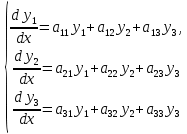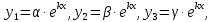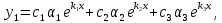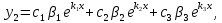курсовая решение систем диф.уравнений. Курсовая работа.Решение систем диф урав. Содержание введение 2 Глава Системы дифференциальных уравнений. 3 Основные понятия и сведения о дифференциальных уравнениях. 3 Системы дифференциальных уравнений.
 Скачать 51.15 Kb. Скачать 51.15 Kb.
|
|
СОДЕРЖАНИЕ ВВЕДЕНИЕ 2 Глава 1. Системы дифференциальных уравнений. 3 1.1.Основные понятия и сведения о дифференциальных уравнениях. 3 1.2.Системы дифференциальных уравнений. Основные понятия. 4 1.3.Интегрирование нормальных систем. 7 1.4.Системы линейных ДУ с постоянными коэффициентами. 10 ЗАКЛЮЧЕНИЕ 17 ЛИТЕРАТУРА 18 ВВЕДЕНИЕ Бурное развитие в последнее десятилетие информационных технологий и компьютерной техники способствует возникновению всё более сложных математических задач, для решения которых требуется значительное время. Очень часто возникают задачи, не требующие абсолютно точного решения; как правило, требуется найти приближенное решение с заданной погрешностью. Одной из таких задач является решение систем дифференциальных уравнений. Обыкновенными дифференциальными уравнениями можно описать поведение материальных точек в силовом поле, законы химической кинетики, уравнения электрических цепей и т. д. Ряд физических задач может быть сведён к решению дифференциальных уравнений или системы дифференциальных уравнений. Целью курсовой работы является рассмотрение решений систем дифференциальных уравнений. Для достижения данной цели решались следующие задачи: изучение основных понятий и сведений о дифференциальных уравнениях; рассмотрение систем дифференциальных уравнений и основных понятий; рассмотрение интегрирования нормальных систем и систем линейных ДУ с постоянными коэффициентами. Глава 1. Системы дифференциальных уравнений. Основные понятия и сведения о дифференциальных уравнениях. При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так, решением уравнения  является функция является функция 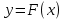 – первообразная для функции – первообразная для функции  . . Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ). Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае – ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ. Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения. Например, уравнение 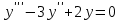 – обыкновенное ДУ третьего порядка, а уравнение – обыкновенное ДУ третьего порядка, а уравнение  – первого порядка; – первого порядка;  ДУ в частных производных первого порядка. ДУ в частных производных первого порядка. Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой. Рассмотрим задачу, решение которой приводит к дифференциальному уравнению. Задача. Материальная точка массы т замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости  . Найти зависимость скорости от времени. Найти скорость точки через . Найти зависимость скорости от времени. Найти скорость точки через 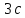 после начала замедления, если после начала замедления, если  Решение. Примем за независимую переменную время  отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки  будет функцией будет функцией 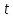 , т.е. , т.е. 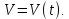 Для нахождения Для нахождения  воспользуемся вторым законом Ньютона (основным законом механики): воспользуемся вторым законом Ньютона (основным законом механики):  где где  - есть ускорение движущегося тела, - есть ускорение движущегося тела,  - результирующая сила, действующая на тело в процессе движения. - результирующая сила, действующая на тело в процессе движения. В данном случае  – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция – коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция  является решением дифференциального уравнения является решением дифференциального уравнения 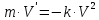 или или  Здесь Здесь 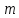 – масса тела. – масса тела. где где  Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления. Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления. Найдем сначала параметры  и и  . Согласно условию задачи, имеем: . Согласно условию задачи, имеем: 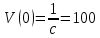 и и  Отсюда Отсюда 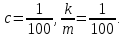 Следовательно, скорость точки изменяется по закону 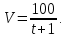 Поэтому Поэтому  Системы дифференциальных уравнений. Основные понятия. Системой дифференциальных уравнений называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные. Общий вид системы ДУ первого порядка, содержащей 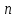 искомых функции искомых функции  следующий: следующий: Система ДУ первого порядка, разрешенных относительно производной, т. е. система вида
называется нормальной системой ДУ. При это предполагается, что число уравнений равно числу искомых функций. Замечание. Во многих случаях системы уравнений и уравнения высших порядков можно привести к нормальной системе вида (1). Так, система трех ДУ второго порядка 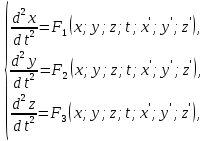 описывающая движение точки в пространстве, путем введения новых переменных:  приводится к нормальной системы ДУ: приводится к нормальной системы ДУ: Уравнение третьего порядка  путем замены путем замены  сводится к нормальной системе ДУ сводится к нормальной системе ДУ Из сказанного выше следует полезность изучения именного нормальных систем. Решение системы (1) называется совокупноcть из 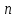 функций функций  удовлетворяющих каждому из уравнений этой системы. удовлетворяющих каждому из уравнений этой системы.Начальные условия для системы (1) имеют вид
Задача Коши для системы (1) ставиться следующим образом: найти решение системы (1), удовлетворяющее начальным условиям (2). Условия существования и единственности решения задачи Коши описывает следующая теорема. Теорема 1. Если в системе (1) все функции  непрерывны вместе со всеми своими частными производными по  в некоторой области в некоторой области  то в каждой точке то в каждой точке 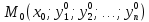 этой области существует, и притом единственное, решение этой области существует, и притом единственное, решение 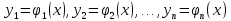 системы, удовлетворяющее начальным условиям (2). системы, удовлетворяющее начальным условиям (2).Меняя в области 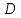 точку точку  (т.е. начальное условия), получим бесчисленное множество решений, которое можно записать в виде решения, зависящего от (т.е. начальное условия), получим бесчисленное множество решений, которое можно записать в виде решения, зависящего от 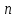 произвольных постоянных: произвольных постоянных: Это решение является общим, если по заданным начальным условиям (2) можно однозначно определить постоянные 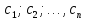 из системы уравнений из системы уравнений Решение, получающееся из общего при конкретных значениях постоянных 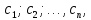 называется частным решением системы (1). называется частным решением системы (1).Интегрирование нормальных систем. Одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача – переход от ДУ к системе – рассмотрена выше на примере). Техника этого метода основана на следующих соображениях. Пусть задана нормальная система (1). Продифференцируем по x любое, например, первое уравнение:  Подставив в это равенство значения производных  из системы (1), получим из системы (1), получим  или, коротко,  Продифференцировав полученное равенство еще раз и заменив значения производных  из системы (1), получим из системы (1), получим Продолжая этот процесс (дифференцируем – подставляем – получаем), находим:  Соберем полученные уравнения в систему:
Из первых  уравнений системы (3) выразим функции уравнений системы (3) выразим функции  через через  , функцию , функцию  и ее производные и ее производные  Получим: Получим:
Найденные значения  подставим в последнее уравнение системы (3). Получим одно ДУ подставим в последнее уравнение системы (3). Получим одно ДУ  порядка относительно искомой функции порядка относительно искомой функции 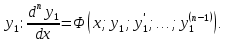 Пусть его общее решение есть Пусть его общее решение есть  Продифференцировав его  раз и подставив значения производных раз и подставив значения производных  в уравнения системы (4), найдем функции в уравнения системы (4), найдем функции   Пример 1. Решить систему уравнений  Решение. Продифференцируем первое уравнение 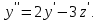 Подставляем Подставляем 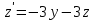 в полученное равенство: в полученное равенство:  Составляем систему уравнений: Составляем систему уравнений: Из первого уравнения системы выражаем  через через 
Подставляем значение  во второе уравнение последней системы: во второе уравнение последней системы: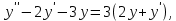 т.е.  Получили одно ЛОДУ второго порядка. Решаем его: Получили одно ЛОДУ второго порядка. Решаем его:  общее решение уравнения. Находим функцию общее решение уравнения. Находим функцию  . Значение . Значение  подставляем в выражение подставляем в выражение  через через  (формула (5)). Получим: (формула (5)). Получим: 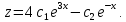 Таким образом, общее решение данной системы уравнений имеет вид 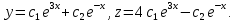 Замечание. Систему уравнений (1) можно решать методом интегрируемых комбинаций, суть метода состоит в том, что посредством арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, т.е. легко интегрируемые уравнения относительно новой неизвестной функции. Проиллюстрируем технику этого метода на следующем примере. Пример 2. Решить систему уравнений:  Решение. Сложим почленно данные уравнения:  или или  Обозначим Обозначим  Тогда имеем Тогда имеем 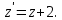 Решаем полученное уравнение: Решаем полученное уравнение:  Получили так называемый первый интеграл системы. Из него можно выразить одну из искомых функций через другую, тем самым уменьшить на единицу число искомых функций. Например,  . Тогда первое уравнение системы примет вид . Тогда первое уравнение системы примет вид 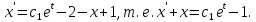 Замечание. Данная система «позволяет» образовать еще одну интегрируемую комбинацию:  Положив Положив  имеем: имеем:  Имеем два первых интеграла системы, то есть Имеем два первых интеграла системы, то есть 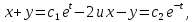 легко найти (складывая и вычитая первые интегралы), что легко найти (складывая и вычитая первые интегралы), что  Системы линейных ДУ с постоянными коэффициентами. Рассмотрим еще один метод интегрирования нормальной системы уравнения (1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, то есть систему вида  Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями 
где все коэффициенты 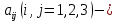 постоянные. постоянные.Будем искать частное решение системы (6) в виде
где  постоянные, которые надо подобрать так, чтобы функции (7) удовлетворяли системе (6). постоянные, которые надо подобрать так, чтобы функции (7) удовлетворяли системе (6).Подставив эти функции в систему (6) и сократив на множитель  , получим: , получим: Или
Систему (8) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными  Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю: Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю:
Уравнение (9) называется характеристическим уравнением системы (6). Раскрыв определитель, получим уравнение третьей степени относительно  . Рассмотрим возможные случаи. . Рассмотрим возможные случаи.Случай 1. Корни характеристического уравнения действительны и различны 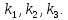 Для каждого корня Для каждого корня 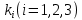 напишем систему (8) и определим коэффициенты напишем систему (8) и определим коэффициенты  (один из коэффициентов можно считать равным единице). Таким образом, получаем: (один из коэффициентов можно считать равным единице). Таким образом, получаем:для корня 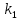 частное решение системы (6): частное решение системы (6):  для корня  для корня  Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (6) записывается в виде
Пример 3. Решить систему уравнений:  Решение. Характеристическое уравнение (9) данной системы имеет вид 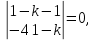 Или  Частные решения данной системы ищем в виде Частные решения данной системы ищем в виде 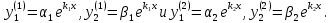 Найдем Найдем 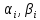 ( (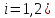 . .При 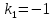 система (8) имеет вид система (8) имеет вид Эта система имеет бесчисленное множество решений. Положим 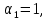 тогда тогда  . Получаем частные решения . Получаем частные решения  При 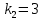 система (8) имеет вид система (8) имеет вид  Положим 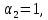 тогда тогда 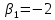 . Значит, корню . Значит, корню 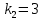 соответствуют частные решения: соответствуют частные решения: . .Общее решение исходной системы, согласно формуле (10), запишется в виде 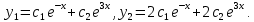 Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные:  Вид частных решений в этой ситуации определяют так же, как и в случае 1. Вид частных решений в этой ситуации определяют так же, как и в случае 1. Замечание. Вместе полученных частных решений можно взять их линейные комбинации, применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида  Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения. При этом понятно, что комплексно сопряжённый корень Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения. При этом понятно, что комплексно сопряжённый корень  не даст новых линейно независимых действительных решений. не даст новых линейно независимых действительных решений. Пример 4. Найти частное решение системы  Удовлетворяющее начальным условиям:  Решение: Составляем и решаем характеристическое уравнение:     Для  получаем: получаем: Отсюда находим:  Частное решение системы: Частное решение системы:  Для  получаем (8): получаем (8):  Отсюда находим:  Частное комплексное решение системы: Частное комплексное решение системы:  В найденных решениях действительную (Re) и мнимую (Im) части: 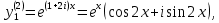      Как уже было сказано, корень  приведет к этим же самым решениям. приведет к этим же самым решениям.Таким образом, общее решение системы имеет вид  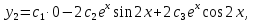 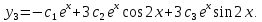 Выделим частное решение системы. При заданных начальных условиях получаем систему уравнений для определения постоянных   Следовательно, искомое частное решение имеет вид   Случай 3. Характеристическое уравнение имеет корень k кратности 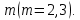 Решение системы, соответствующее кратному корню, следует кратному корню, следует искать в виде: Решение системы, соответствующее кратному корню, следует кратному корню, следует искать в виде: а) если  то то  б) если 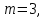 то то  Это решение зависит от 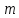 произвольных постоянных. Постоянные произвольных постоянных. Постоянные 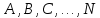 определяются методом неопределённых коэффициентов. Выразив все коэффициенты через определяются методом неопределённых коэффициентов. Выразив все коэффициенты через 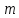 из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим 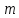 линейно независимых частных решений системы (6). линейно независимых частных решений системы (6).Пример 5. Решить систему уравнений:  Решение. Составляем и решаем характеристическое уравнение   Корню Корню 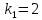 соответствует система: соответствует система: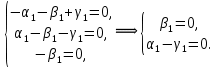 Полагая  находим находим 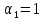 . Получаем одно частное решение исходной системы: . Получаем одно частное решение исходной системы:  Двукратному корню 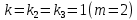 соответствует решение вида соответствует решение вида  Подставляем эти выражения (решения) в уравнения исходной системы: Подставляем эти выражения (решения) в уравнения исходной системы: 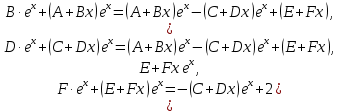 или, после сокращение на  и группировки, и группировки,  Эти равенства тождественно выполняются лишь в случае, когда  Выразим все коэффициенты через два из них  например, через например, через  Из второго уравнения имеем Из второго уравнения имеем  Тогда, учетом первого уравнения, получаем Тогда, учетом первого уравнения, получаем  Из четвертого уравнения находим Из четвертого уравнения находим  т.е. т.е. 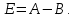 Из третьего уравнения: Из третьего уравнения:  Коэффициенты Коэффициенты 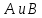 – произвольные. – произвольные. Полагая 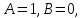 находим: находим:  Полагая  находим: находим:  Получаем два линейно независимых частных решения, соответствующих двукратному корню  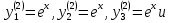 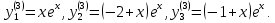 Записываем общее решение исходной системы:   ЗАКЛЮЧЕНИЕ В результате работы поставленные задачи выполнены, цель достигнута. Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким ДУ, образующим систему. Задача решения системы дифференциальных уравнений имеет важное прикладное значение при решении научных и технических проблем. Кроме того, она является вспомогательной задачей при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований. ЛИТЕРАТУРА Письменный, Д. Т./ Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - 10-е изд., испр. - М.: Айрис-пресс, 2011. - 608 с. Лунгу К. Н./ Сборник задач по высшей математике. 2 курс/ Лунгу К.Н. и др.; под ред. Федина С.Н. – 6-е. изд. – М.: Айрис – пресс, 2007. – 592 с. Ильин В.А./ Классический университетский учебник МГУ «Высшая математика» В.А. Ильин, А.В. Куркина / 2011г.- 592 с. Боярчук А.К./ Дифференциальные уравнения в примерах и задачах/ Боярчук А.К., Головач Г.П./ справочное пособие по высшей математике// М: Эдиториал УРСС, 2001- 384 с. Гунько В.Д./ Дифференциальные уравнения. Примеры и типовые задания// Гунько В.Д., Суховеева Л.Ю., Смоленцев В.М: Учебное пособие/ КубГАУ. – Краснодар, 2005 – 105с. |