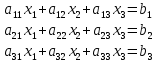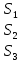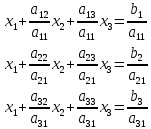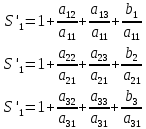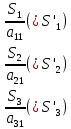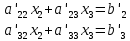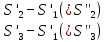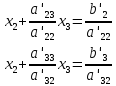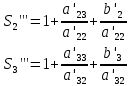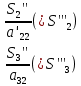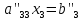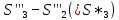лабораторная работа 3. Лабораторная работа № 3. Лабораторная работа 3 Решение систем линейных уравнений Цель работы Решение систем линейных уравнений с помощью различных методов
 Скачать 20.41 Kb.
|
|
Лабораторная работа №3 Решение систем линейных уравнений 1.Цель работы Решение систем линейных уравнений с помощью различных методов. 2.Задание: вариант 2 Методами Зейделя и Гаусса решить систему линейных уравнений с точностью ε=10-3.  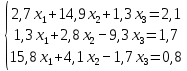 (1)3.Расчётная часть Методом Зейделя А) Краткое теоретическое введение Допустим, диагональные коэффициенты исходной матрицы {aij}отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему (1) в следующем виде: 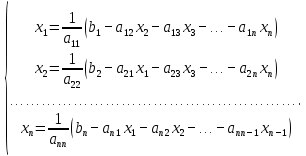 (2)Если теперь задать для неизвестных их начальные приближенные значения x(0)n,n=1,2,3 то система (2) позволяет вычислить более точные значения неизвестных на первом шаге (на первой итерации): 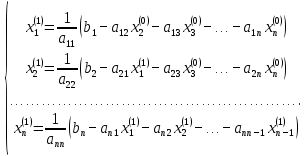 Используя найденные значения неизвестных, можно еще более уточнить их на второй итерации: 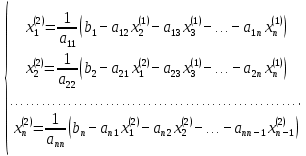 и так далее. Общую формулу определения i-го неизвестного на k-й итерации для системы n уравнений можно записать так: 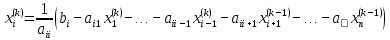 i=1,2,3,…,n; k=1,2,3,… Итерационный процесс продолжается до тех пор, пока все значения xi(k), не станут достаточно близкими к xi(k-1). 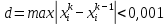 Б) Ручной расчёт 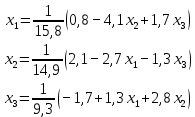 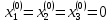 Первый шаг: 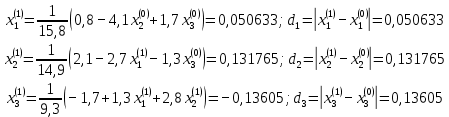 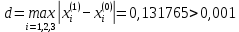 продолжать расчётВторой шаг: 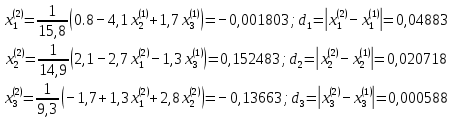 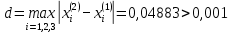 продолжать расчётТретий шаг: 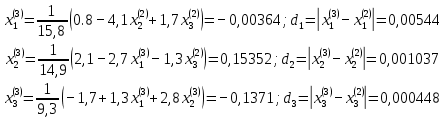  продолжать расчётИ так далее Следующие шаги приведены в таблице:
В) Результат 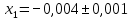 ;  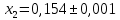;  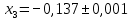Методом Гаусса А) краткое теоретическое введение В общем виде система трех линейных уравнений с тремя неизвестными имеет вид: 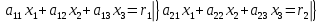 (1)Предположим, что хотя бы один из коэффициентов при неизвестном x1 отличен от нуля; пусть таким является коэффициент a11. Разделим все члены первого уравнения системы (1) на a11, затем все члены второго уравнения – на a21, все члены третьего уравнения – на a31. Если a21 или a31 равен нулю, то соответствующее уравнение входит в новую систему без изменений. 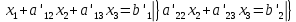 (2)Предположим, что в системе (2) хотя бы один из коэффициентов a’22 или a’32 отличен от нуля. Пусть таким является, например, коэффициент a’22. разделим почленно второе уравнение системы (2) на a’22, третье – на a’32. затем из третьего полученного уравнения вычтем второе полученное уравнение. В результате этих преобразований система примет вид: 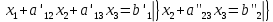 (3)Число, равное суме всех коэффициентов данного уравнения, включая его свободный член, будем называть строчной суммой. Контрольной суммой будем называть то число, которое на первом этапе совпадает с соответствующей строчной суммой, а на последующих этапах получается из контрольных сумм предыдущего этапа в результате того же преобразования, которое проводится над соответствующим уравнением. Строчные суммы обладают свойством, которое используется при контроле: При замене правых частей системы уравнений соответствующими строчными суммами получается система уравнений такая, что если x1, x2, x3 есть решение первоначальной системы, то x1+1, x2+1, x3+1 будет решение новой системы. Числа x’1=x1+1; x’2=x2+1; x’3=x3+1 удовлетворяют первому уравнению новой системы (1). Наряду с системами (1), (2), (3), будем иметь в виду еще три системы (1’), (2’), (3’). Левые части параллельных пар систем (1) и (1’), (2) и (2’), (3) и (3’) соответственно совпадают, а правые части систем (1’), (2’), (3’) получаются заменой свободных членов системы (1), (2), (3) соответствующими строчными суммами. Системы (1), (2), (3) эквивалентны между собой; системы (1’), (2’), (3’) – также эквивалентны между собой. Причем система (3’) имеет вид: 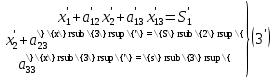 Используя «обратный ход», из системы (3) последовательно находим x3, x2, x1; параллельно из системы (3’) последовательно находим x’3, x’2, x’1. Числа x3 и x’3, x2 и x’2 , x1 и x’1 должны отличаться на 1 (расхождение в запасных знаках во внимание не принимается).
 , где   .
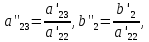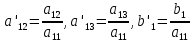Б) Ручной расчёт
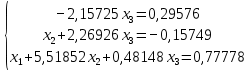
В) Результат 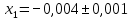; ; 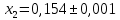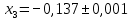Работу выполнил студент группы 1-31 Баринов Владимир | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
