Содержание. Введение Парная регрессия и корреляция в экономических исследованиях Линейная парная регрессия Корреляция Заключение Список литературы Введение
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
 Содержание. Введение………………………………………………………………………………………………..…….3 1. Парная регрессия и корреляция в экономических исследованиях………..5 2. Линейная парная регрессия……………………………………………………………………..7 3. Корреляция…………………………………………………………………………………….…….….19 Заключение……………………………………………………………………………………….……..….21 Список литературы……………………………………………………………………………..……….22 Введение. Единое общепринятое понятие эконометрики в настоящие время отсутствует. Сам термин «Эконометрика» был введен в 1926 году норвежским ученным Р.Фришем и в дословном переводе означает «экономические измерения». Наряду с таким широким пониманием эконометрики, порождаемым переводом самого термина, встречается и весьма узкая трактовка эконометрики как набора математическо-статистических методов, используемых в приложениях математики в экономике. Приводимые ниже определения и высказывания известных ученных позволяют получить представление о различных толкованиях эконометрики. Эконометрика – это раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными (С.Фишер) Основная задача эконометрики – наполнить эмпирическим содержанием априорные экономические рассуждения (Л.Кейн) Цель эконометрики – эмпирический вывод экономических законов (Э.Маленово). Эконометрика является не более чем набором инструментов, хотя и очень полезных. Эконометрика является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира (Ц.Трилехес). Р. Фриш указывает на то, что эконометрика есть единство трех составляющих – статистики, экономической теории и математики. С.А.Айвазян полагает, что эконометрика объединяет совокупность методов и моделей позволяющих на базе экономической теории, экономической статистики и математики констатического инструментария придавать количественные выражения качественными зависимостями. Основные результаты экономической теории носят качественный характер, а эконометрика вносит в них эмпирическое содержание. Математическая экономика выражает экономические законы в виде математических соотношений, а эконометрика осуществляет опытную проверку этих законов. Экономическая статистика дает информационное обеспечение исследуемого процесса в виде исходных (обрабатываемых) статистических и экономических показателей, а эконометрика, используя традиционные математически статистические и специально разрабатываемые методы, проводит анализ количественных взаимосвязей между этими показателями. Многие базовые понятия эконометрики имеют два определения – экономическое и математическое. Подобная двойственность имеет место и в формулировках результатов. Характер научных работ по эконометрике варьируется от «классических» экономических работ, в которых почти не используется математический аппарат, до солидных математических трудов, использующих достаточно тонкий аппарат современной математики. Экономическая составляющая эконометрии, безусловно, является первичной. Именно экономика определяет постановку задачи и исходные предпосылки, а результат, формируемый на математическом языке, представляет интерес лишь в том случае, если удается его экономическая интерпретация. В то же время многие эконометрические результаты носят характер математических утверждений (теорем). Широкому внедрению эконометрических методов способствовало появление во второй половине ХХ века ЭВМ и в частности персональных компьютеров. Компьютерные эконометрические пакеты сделали эти методы более доступными и наглядными так как всю наиболее трудоемкую работу, по расчетам статистики, параметров, построению таблиц и графиков в основном стал выполнять компьютер, а эконометристу осталась главным образом: постановка задачи, выбор соответствующих моделей и методов её решения, интерпретации результатов. 1. Парная регрессия и корреляция в экономических исследованиях. Простая регрессия – регрессия между двумя переменными – у и х, т.е. модели вида у= f(х) где у - зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная (признак - фактор). Множественная регрессия – регрессия результативного признака с двумя м большим числом факторов, т.е. модель вида: у=f(х1,х2,…..,хк). Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями. Практически в каждом отдельном случае величина у складывается из двух слагаемых: уi=уxi+εi где уi – фактическое значение результативного признака; уxi – теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т.е. из уравнения регрессии; εi – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. В парной регрессии выбор вида математической функции у= f(х) может быть осуществлен тремя методами:
Метод наименьших квадратов (МНК) – классический подход к оценке параметров линейной регрессии. МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) ух минимальна Σ(уi-yxi)2 min. Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояния по вертикали между точками и этой линией была минимальной. Нелинейная регрессия – если между экономическими явлениями существуют соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий:
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция у=ахbε. Связано это с тем что параметр b в ней имеет четкое экономическое истолкование, т.е. он является коэффициентом эластичности. Это означает, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент детерминации – характеристика практической силы анализируемой регрессионной модели. Критерий Фишера (F) – показывает в какой мере регрессия лучше оценивает значение переменной по сравнению с ее средней. 2. Линейная парная регрессия Корреляционная зависимость может быть представлена в виде Mx(Y) = (x) (1) или My(X) = (у), где (x) const, (у) const. В регрессионном анализе рассматривается односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной Х. Такая зависимость Y от X (иногда ее называют регрессионной) может быть также представлена в виде модельного уравнения регрессии Y от X (1). При этом зависимую переменную Yназывают также функцией отклика(объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком), а независимую переменную Х – объясняющей(входной, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором, факторным признаком). Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х, т.е. Х = х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (xi, yi) ограниченного объема n. В этом случае речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии: где Уравнение (2) называется выборочным уравнением регрессии. В дальнейшем рассмотрим линейную модель и представим ее в виде Для решения поставленной задачи определим формулы расчета неизвестных параметров уравнения линейной регрессии (b0, b1). Согласно методу наименьших квадратов (МНК) неизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений На основании необходимого условия экстремума функции двух переменных S = S(b0, b1) (4) приравняем к нулю ее частные производные, т.е. 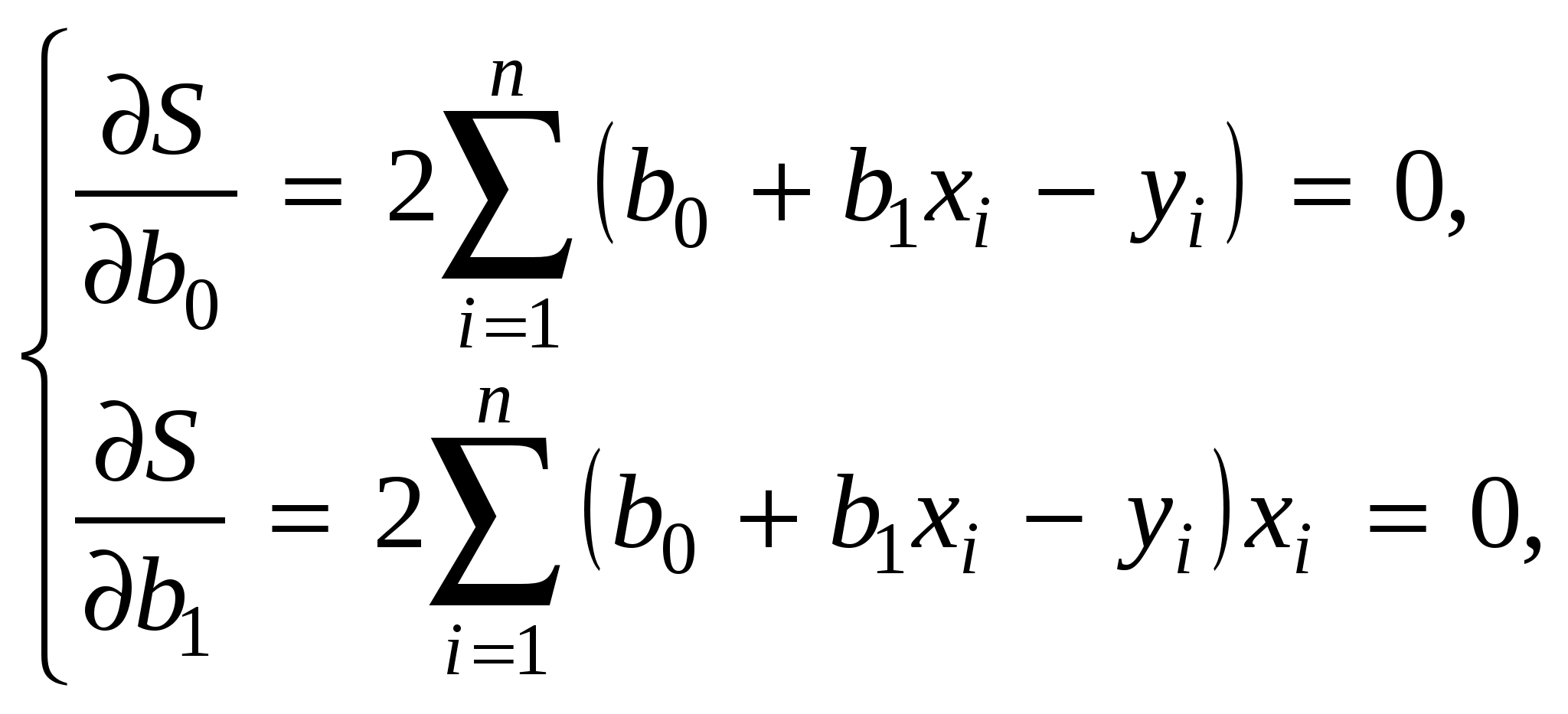 откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии: (5) Теперь, разделив обе части уравнений (5) на n, получим систему нормальных уравнений в следующем виде: где соответствующие средние определяются по формулам: 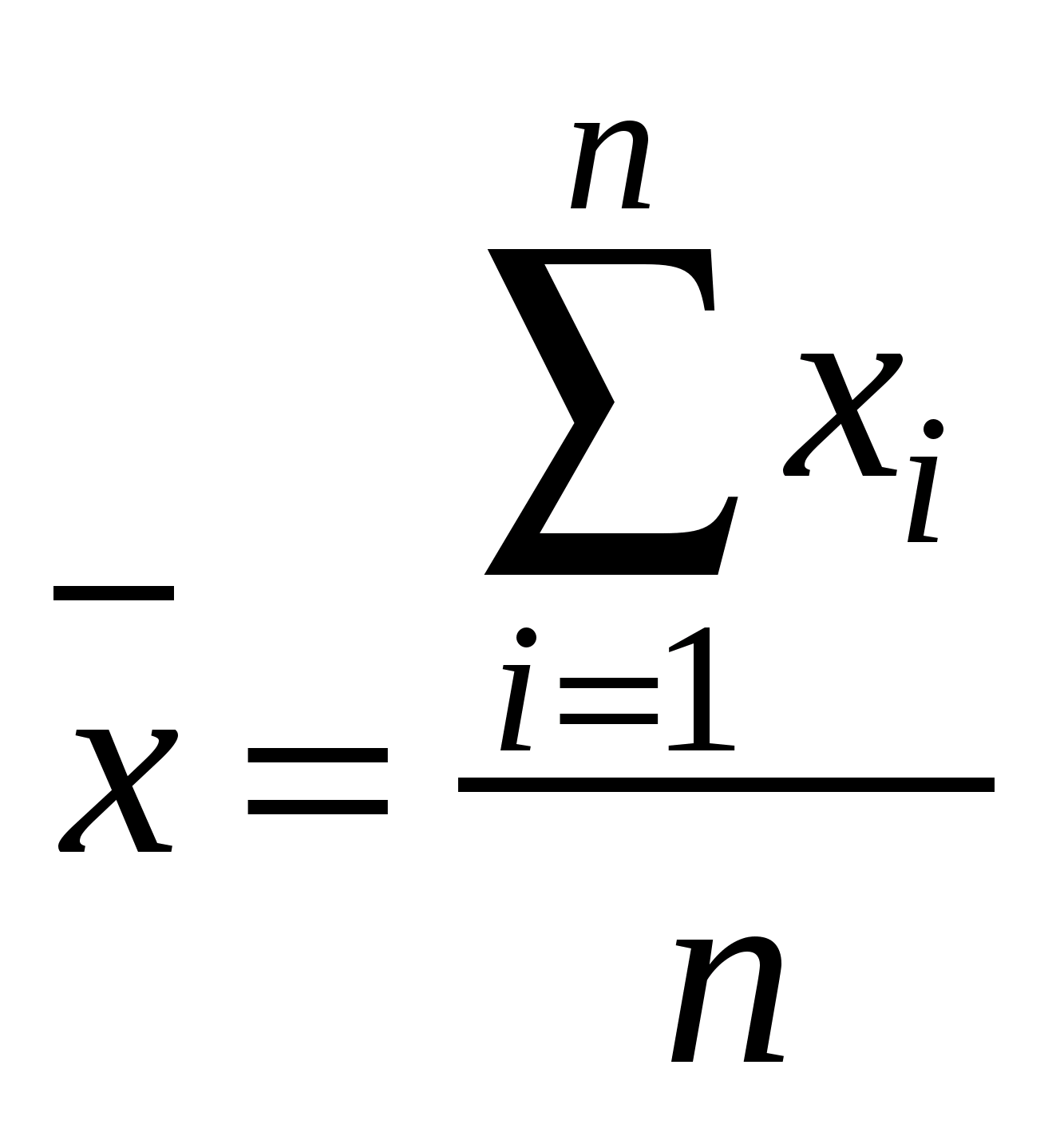 ; (7) ; (7) 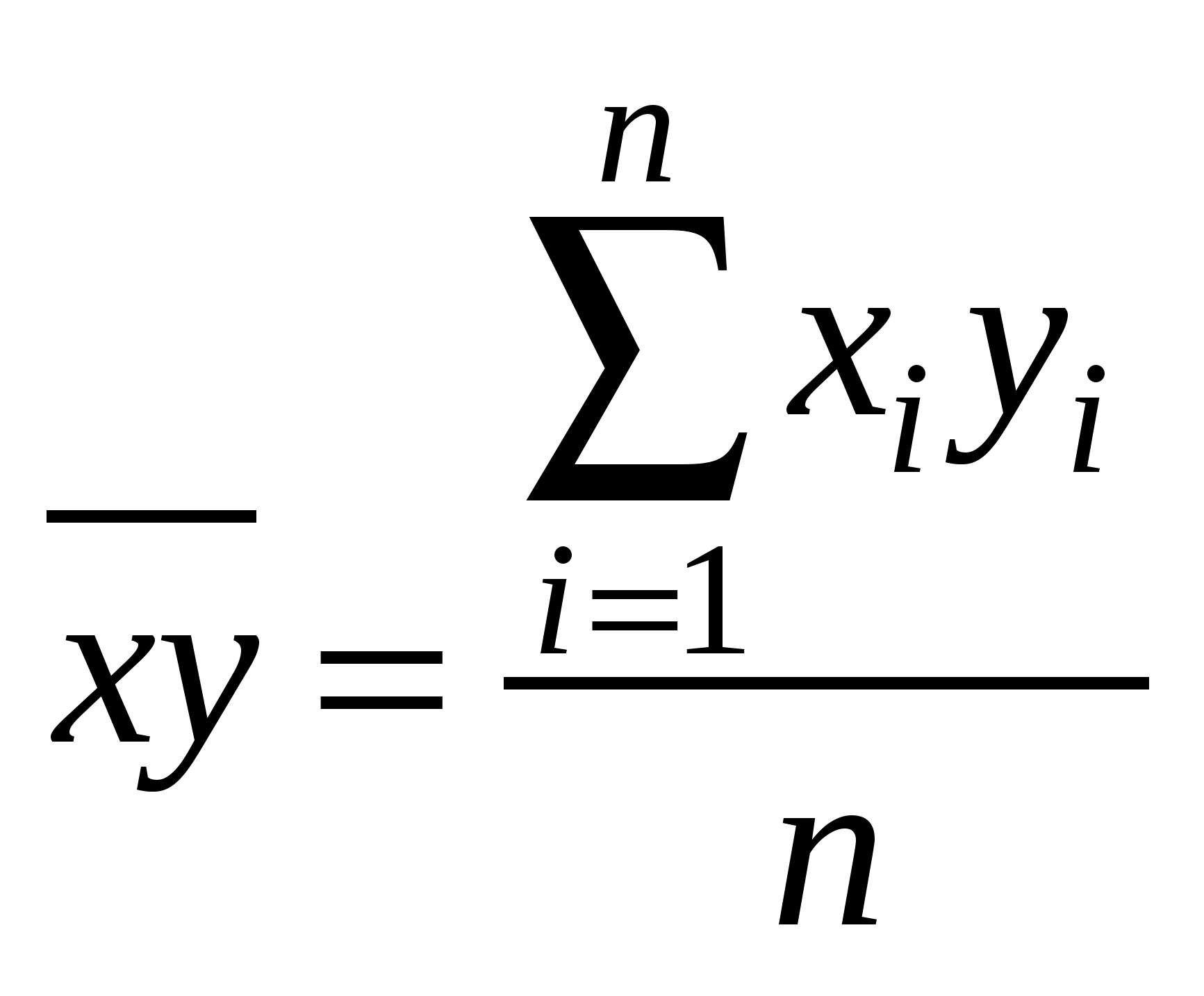 ; (9) ; (9); (8) 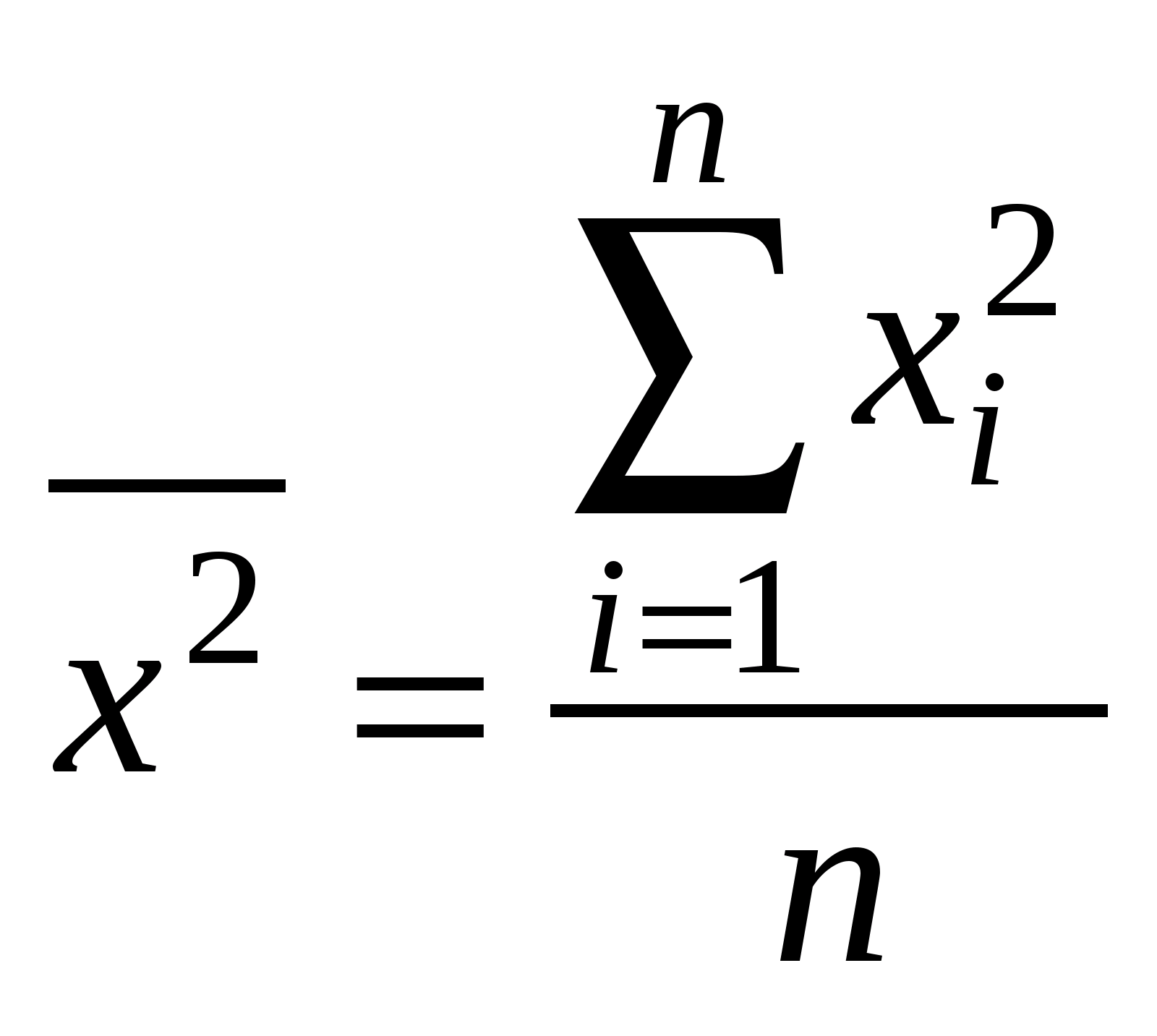 . (10) . (10)Решая систему (6), найдем где  , (12) , (12)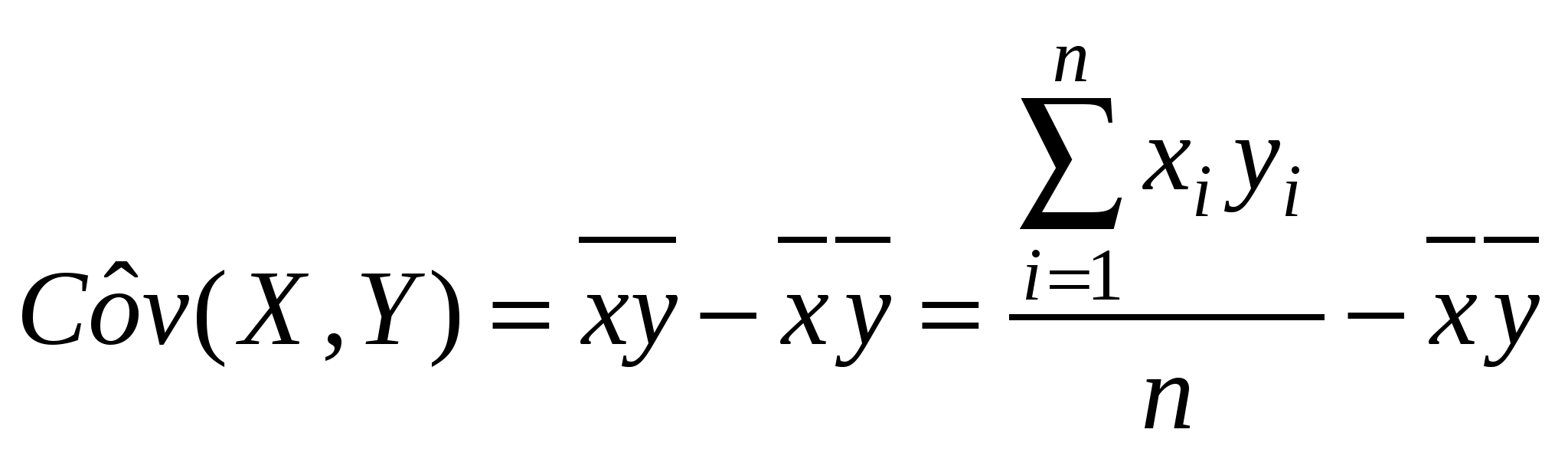 . (13) . (13)Коэффициент b1 называется выборочным коэффициентом регрессии Y по X. Коэффициент регрессии Y по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу. Отметим, что из уравнения регрессии На первый взгляд, подходящим измерителем тесноты связи Y от Х является коэффициент регрессии b1. Однако b1 зависит от единиц измерения переменных. Очевидно, что для "исправления" b1 как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Если представить уравнение В этой системе величина Если r > 0 (b1 > 0), то корреляционная связь между переменными называется прямой, если r < 0 (b1 < 0), обратной. Учитывая (7)–(13) получим следующие формулы для расчета коэффициента корреляции: 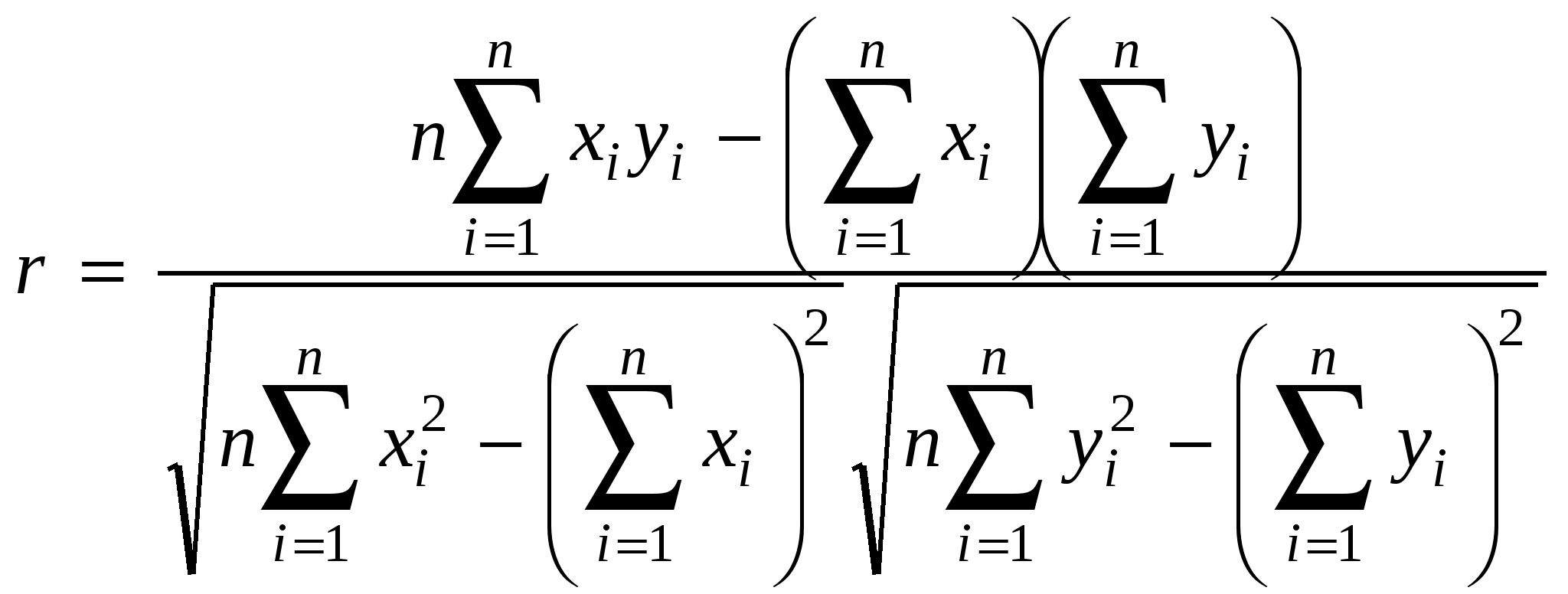 . (16) . (16)Выборочный коэффициент корреляции обладает следующими свойствами: 1.Коэффициент корреляции принимает значения на отрезке [1: 1], т.е. 1 ≤ r ≥ 1. 2.При r=±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдения располагаются на прямой линии. 3. При r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси ОХ. В силу воздействия неучтенных факторов и причин отдельные наблюдения переменной Y будут в большей или меньшей мере отклоняться от функции регрессии (Х). В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлена в виде: Y = (X) + , где случайная переменная (случайный член), характеризующая отклонение от функции регрессии. Рассмотрим линейный регрессионный анализ, для которого унция (Х) линейна относительно оцениваемых параметров: Mx(Y) = 0 + 1x.(17) Предположим, что для оценки параметров линейной функции регрессии (17) взята выборка, содержащая п пар значений переменных (xi, yi), где i = 1, 2, …, п. В этом случае линейная парная регрессионная модель имеет вид: yi = 0 + 1xi + i. (18) Отметим основные предпосылки регрессионного анализа (условия Гаусса-Маркова). 1. В модели yi = 0 + 1xi + i возмущение iесть величина случайная, а объясняющая переменная xi– величина неслучайная. 2. Математическое ожидание возмущения iравно нулю: M(i) = 0. (19) 3. Дисперсия возмущения i постоянна для любого i: D(i) = 2. (20) 4. Возмущения i и jне коррелированны: M(i j) = 0 (i j). (21) 5. Возмущения iесть нормально распределенная случайная величина. Оценкой модели (18) по выборке является уравнение регрессии Теорема ГауссаМаркова. Если регрессионная модель yi = 0 + 1xi + i удовлетворяет предпосылкам 15, то оценки b0, b1 имеют наименьшую дисперсию в классе всех линейных несмещенных оценок. Таким образом, оценки b0 и b1 в определенном смысле являются наиболее эффективными линейными оценками параметров 0 и 1. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Для проверки значимости выдвигают нулевую гипотезу о надежности параметров. Вспомним основные понятия и определения необходимые для анализа значимости параметров регрессии. Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным. Нулевая гипотеза Н0 – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверить ее. Так как проверку производят статистическими методами, то данная проверка называется статистической. При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов: можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода); можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода). Допустимая вероятность ошибки первого рода может быть равна 5% или 1% (0,05 или 0,01). Уровень значимости – это вероятность ошибки первого рода при принятии решения (вероятность ошибочного отклонения нулевой гипотезы). Альтернативные гипотезы принимаются тогда и только тогда, когда опровергается нулевая гипотеза. Это бывает в случаях, когда различия в средних арифметических экспериментальной и контрольной групп настолько значимы (статистически достоверны), что риск ошибки отвергнуть нулевую гипотезу и принять альтернативную не превышает одного из трех принятых уровней значимости статистического вывода: 1-йуровень 5% ( = 0,05), где допускается риск ошибки в выводе в пяти случаях из ста теоретически возможных таких же экспериментов при строго случайном отборе для каждого эксперимента; 2-й уровень 1% ( = 0,01), т. е. соответственно допускается риск ошибиться только в одном случае из ста; 3-й уровень 0,1% ( = 0,01), т. е. допускается риск ошибиться только в одном случае из тысячи. Последний уровень значимости предъявляет очень высокие требования к обоснованию достоверности результатов эксперимента и потому редко используется. В эконометрических исследованиях, не нуждающихся в очень высоком уровне достоверности, представляется разумным принять 5%-й уровень значимости. Статистика критерия некоторая функция от исходных данных, по значению которой проверяется нулевая гипотеза. Чаще всего статистика критерия является числовой функцией. Всякое правило, на основе которого отклоняется или принимается нулевая гипотеза, называется критериемпроверки данной гипотезы. Статистический критерий – это случайная величина, которая служит для проверки статистических гипотез. Критическая область – совокупность значений критерия, при котором нулевую гипотезу отвергают. Область принятия нулевой гипотезы (область допустимых значений) – совокупность значений критерия, при котором нулевую гипотезу принимают. При справедливости нулевой гипотезы вероятность того, что статистика критерия попадает в область принятия нулевой гипотезы должна быть равна 1. Процедура проверки нулевой гипотезы в общем случае включает следующие этапы:
В современных эконометрических программах (например, EViews) используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначенные обычно Prob, могут иметь различное числовое выражение в интервале от 0 до 1, например, 0,7, 0,23 или 0,012. Понятно, что в первых двух случаях, полученные уровни значимости слишком велики и говорить о том, что результат значим нельзя. В последнем случае результаты значимы на уровне двенадцати тысячных. Если вычисленное значение Рrob превосходит выбранный уровень Рrobкр, то принимается нулевая гипотеза, а в противном случае альтернативная гипотеза. Чем меньше вычисленное значение Рrob, тем более исходные данные противоречат нулевой гипотезе. Число степеней свободы у какого-либо параметра определяют как размер выборки, по которой рассчитан данный параметр, минус количество выбранных переменных. Величина W называется мощностью критерия и представляет собой вероятность отклонения неверной нулевой гипотезы, т.е. вероятность правильного решения. Мощность критерия – вероятность попадания критерия в критическую область при условии, что справедлива альтернативная гипотеза. Чем больше W, тем вероятность ошибки второго рода меньше. Коэффициент регрессии (b1) является случайной величиной. Отсюда после вычисления возникает необходимость проверки гипотезы о значимости полученного значения. Выдвигаем нулевую гипотеза (Н0) о равенстве нулю коэффициента регрессии (Н0:b1 = 0) против альтернативной гипотезы (Н1) о неравенстве нулю коэффициента регрессии (Н1:b1 0). Для проверки гипотезы Н0 против альтернативы используется t-статистика, которая имеет распределение Стьюдента с (n 2) степенями свободы (парная линейная регрессия). Коэффициент регрессии надежно отличается от нуля (отвергается нулевая гипотеза Н0), если tнабл > t;n-2. В этом случае вероятность нулевой гипотезы (Prob.) будет меньше выбранного уровня значимости. t;n-2 критическая точка, определяемая по математико-статистическим таблицам. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Согласно основной идее дисперсионного анализа 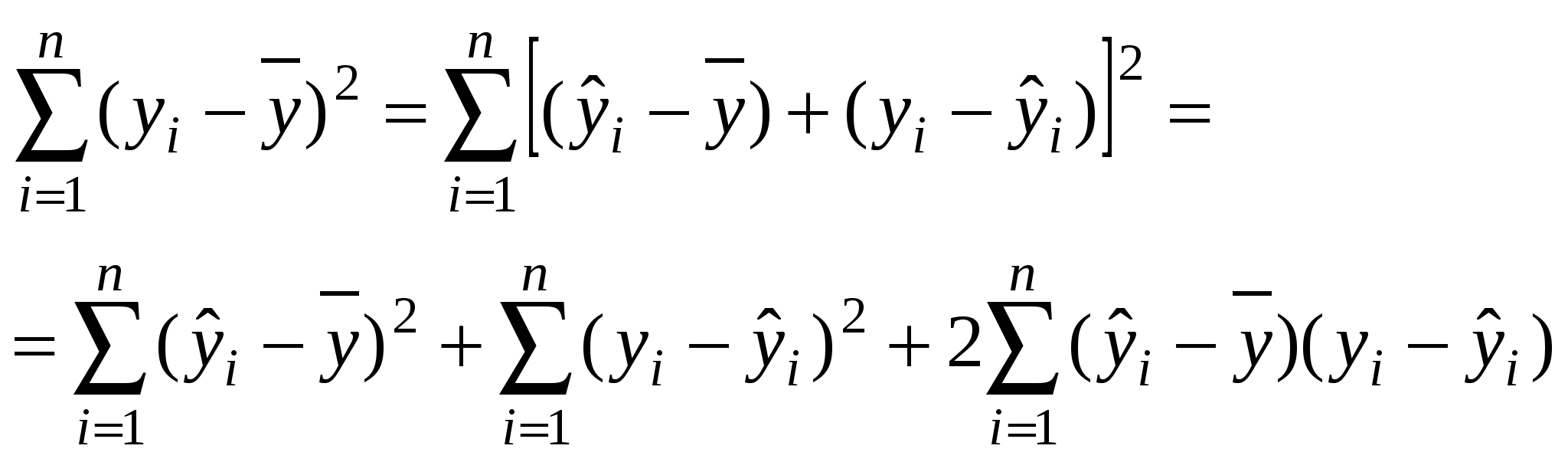 (22) (22)или Q = QR + Qe, (23) где Q – общая сумма квадратов отклонений зависимой переменной от средней, а QR и Qe – соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов. Схема дисперсионного анализа имеет вид, представленный в табл. 1. Средние квадраты При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины и Таблица 1
Поэтому уравнение регрессии значимо на уровне , если фактически наблюдаемое значение статистики где Учитывая смысл величин Для парной линейно регрессии т = 2, и уравнение регрессии значимо на уровне (отвергается нулевая гипотеза) Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии b1, который имеет t-распределение Стьюдента с k = n – 2 степенями свободы. Уравнение парной регрессии или коэффициент регрессии b1 значимы на уровне (иначе – гипотеза Н0 о равенстве параметра b1 нулю, т.е. Н0:b1 = 0, отвергается), если фактически наблюдаемое значение статистики больше критического (по абсолютной величине), т.е. |t| > t1 ; n 2. Коэффициент корреляции r значим на уровне (Н0: r = 0), если Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле: Величина R2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной. В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату корреляции, т.е. R2 = r2. Доверительный интервал для индивидуальных значений зависимой переменной где 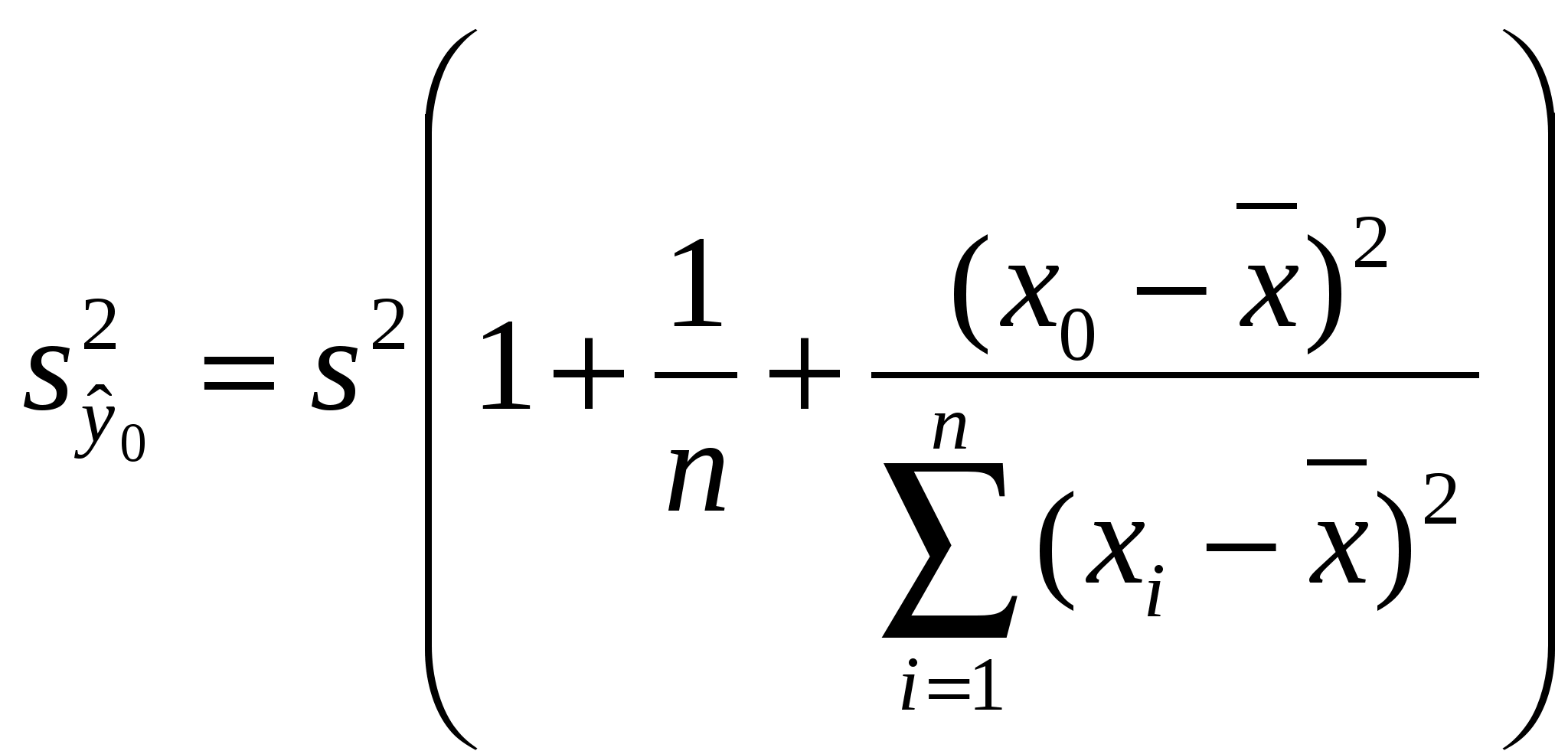 оценка дисперсии индивидуальных значений у0 при х = х0. оценка дисперсии индивидуальных значений у0 при х = х0.Доверительный интервал для параметров регрессионной модели. 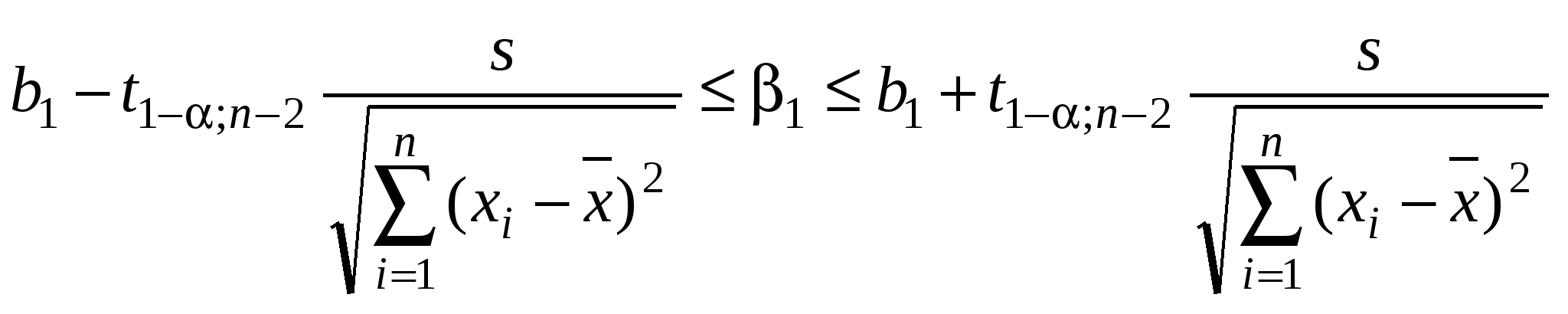 (30) (30)3. Корреляция. "корреляция" — стохастическая, вероятная, возможная связь между двумя (парная) или несколькими (множественная) случайными величинами. если для двух случайных величин X и Y имеет место равенство P(X ÇY) = P(X)·P(Y), то эти величины считаются независимыми. Ну, а если это не так!? Ведь всегда важно знать: насколько зависит одна СВ от другой? Дело не только в присущем людям стремлении анализировать что-либо обязательно в числовом измерении. Уже понятно, что прикладная статистика требует непрерывных вычислений, что использование компьютера вынуждает нас работать с числами, а не с понятиями. Для числовой оценки взаимосвязи между двумя СВ: Y – с известными M(Y) и sy и X – с M(X) и sx принято использовать так называемый коэффициент корреляции 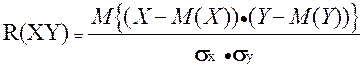 . {3–1} . {3–1}Обратим внимание на способ вычисления коэффициента корреляции. В числителе находится математическое ожидание произведения отклонений величин X и Y от собственных математических ожиданий. Этот коэффициент может принимать значения от –1 до +1 — в зависимости от тесноты и характера связи между данными СВ. Если коэффициент корреляции равен нулю, то X и Y называют некоррелированными. Считать их независимыми обычно нет оснований — оказывается, что существуют такие, как правило — нелинейные связи величин, при которых коэффициент корреляции равен нулю, хотя величины зависят друг от друга. Обратное всегда верно — если величины независимы, то R(XY) = 0. Но, если модуль R(XY) равен 1, то есть все основания предполагать наличие линейной связи между Y и X. Именно поэтому часто говорят о линейной корреляции при использовании такого способа оценки связи между СВ. Если у нас имеется ряд наблюдений за двумя случайными величинами, то можно оценить выборочное значение коэффициента корреляции – 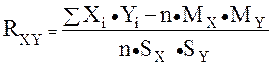 {3–2} {3–2}Оценку корреляционной связи двух СВ можно производить и без учета их дисперсий. Числитель коэффициента корреляции называют ковариацией случайных величин, которая также служит мерой связи, но без непосредственного учета дисперсий. Различие между такими двумя показателями парной связи СВ достаточно существенное. · Коэффициент корреляции определяет степень, тесноту линейной связи между величинами и является безразмерной величиной. · Ковариация двух СВ определяет эту связь безотносительно к ее виду и является величиной размерной. Заключение.Корреляционно-регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи.Наиболее разработанной в теории статистики является методология парной корреляции, рассматривающая влияние вариации факторного признака х на результативный у и представляющая собой однофакторный корреляционный и регрессионный анализ. Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна. Ряд авторов считают корреляционный анализ частью регрессионного анализа, а другие полагают, что регрессионный анализ является частью корреляционного, как общей теории взаимосвязи между случайными величинами. Практически, речь идет о том, чтобы анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности, точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию) - линию регрессии.Список литературы.1. Айвазян, С. А. Эконометрика / С.А. Айвазян, С.С. Иванова. - М.: Маркет ДС, 2017. - 104 c.2. Артамонов, Н. В. Введение в эконометрику / Н.В. Артамонов. - М.: МЦНМО, 2016. - 224 c. 3. Гладилин, А. В. Практикум по эконометрике / А.В. Гладилин, А.Н. Герасимов, Е.И. Громов. - М.: Феникс, 2016. - 336 c. 4. Колемаев, В. А. Эконометрика / В.А. Колемаев. - М.: ИНФРА-М, 2016. - 160 c. 5. Кочетыгов, А. А. Основы эконометрики / А.А. Кочетыгов, Л.А. Толоконников. - М.: Издательский центр "МарТ", 2015. - 352 c. |
