Реализация логических функций. Содержание задание Схемы основных логических элементов 3 Задание Создание схемы заданной функции 4 Задание Схема в Combinatorial Logic 5 Задание Представление
 Скачать 105.75 Kb. Скачать 105.75 Kb.
|
|
СОДЕРЖАНИЕ Задание 1. Схемы основных логических элементов 3 Задание 2. Создание схемы заданной функции 4 Задание 3. Схема в Combinatorial Logic 5 Задание 4. Представление логической функции в СКНФ и СДНФ 6 Задание 5. Схемы СКНФ и СДНФ 7 Задание 6. Выводы 9 Задание 1. Схемы основных логических элементовИспользуя блок Logical Operation, смоделировать работу логических элементов, реализующих логические функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ при всех возможных значениях аргументов и заполнить табл. 1. Реализуем функции в Matlab (Simulink), получаем схему на рисунке 1: 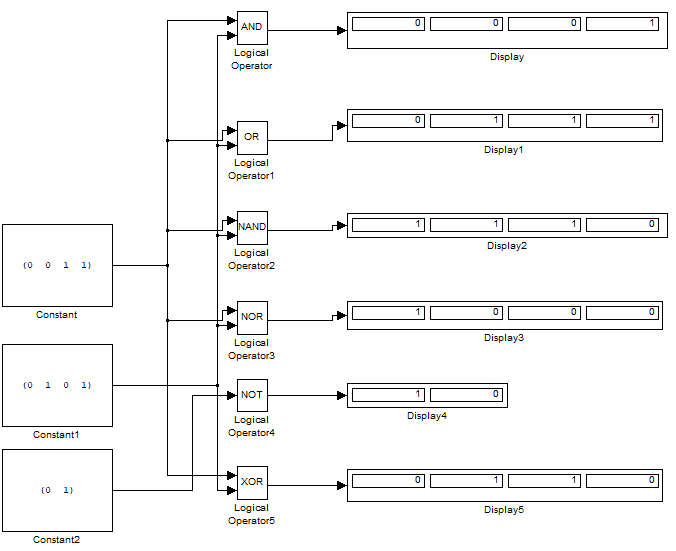 Рисунок 1 – Моделирование задания 1 в Matlab Заполняем таблицу 1 в соответствии с заданием, получаем: Таблица 1 – Результат моделирования логических функций:
Задание 2. Создание схемы заданной функцииВ соответствии со своим вариантом задания (таблица 3) собрать схему, реализующую заданную формулу (использовать блок Logical Operation) и промоделировать ее работу. По результатам моделирования заполнить таблицу истинности функции. Заданная функция: 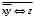 Схема, собранная в Matlab приведена на рисунке 2 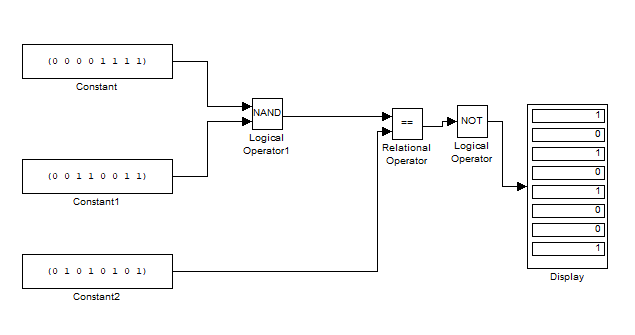 Рисунок 2 – Схема заданной функции Таблица истинности функции приведена в таблице 2. Таблица 2 – Таблица истинности функции
Задание 3. Схема в Combinatorial LogicСобрать схему, реализующую формулу из п. 2. Для выполнения задания необходимо использовать блок Combinatorial Logic и полученную в п.2 таблицу истинности функции. Схема, собранная в Matlab, приведена на рисунке 3 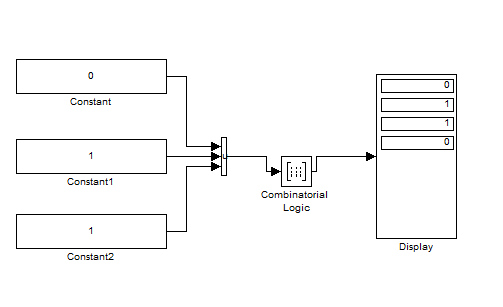 Рисунок 3 – Схема, собранная с помощью блока Combinatorial Logic и таблицы истинности Задание 4. Представление логической функции в СКНФ и СДНФИспользуя таблицу истинности функции, полученную в п. 2, представить заданную логическую функцию в СКНФ и СДНФ. Представляем заданную логическую функцию в СКНФ и СДНФ: Построение совершенной дизъюнктивной нормальной формы: Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 0 } { 0, 1, 0 } { 1, 0, 0 } { 1, 1, 1 } В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием: K1: { 0, 0, 0 } – 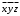 K2: { 0, 1, 0 } – 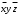 K3: { 1, 0, 0 } – 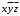 K4: { 1, 1, 1 } – 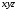 Объединим конъюнкции с помощью операции ИЛИ и получим совершенную дизъюнктивную нормальную форму: K1 ∨ K2 ∨ K3 ∨ K4 = 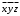 ∨ ∨ 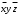 ∨ ∨ 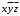 ∨ ∨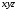 Построение совершенной конъюнктивной нормальной формы: Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 1 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 0 } В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием: D1: { 0, 0, 1 } – 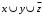 D2: { 0, 1, 1 } – 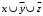 D3: { 1, 0, 1 } – 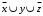 D4: { 1, 1, 0 } – 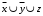 Объединим дизъюнкции с помощью операции И и получим совершенную конъюнктивную нормальную форму: D1 ∧ D2 ∧ D3 ∧ D4 = ( 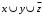 ) ∧ ( ) ∧ (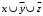 ) ∧ ( ) ∧ (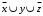 ) ∧ ( ) ∧ (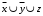 ) )Задание 5. Схемы СКНФ и СДНФСобрать схемы реализующие СКНФ и СДНФ. Промоделировать их работу и по результатам моделирования построить таблицы истинности. Схемы, построенные по данным формам представлены на рисунках 4 и 5. Схема реализации СДНФ в Simulink представлена на рисунке 4: 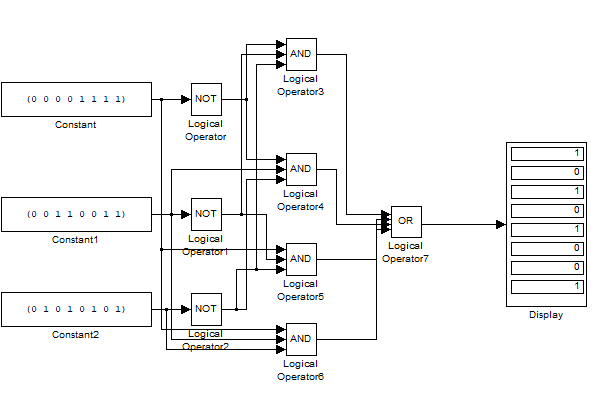 Рисунок 4 – Схема реализации СДНФ Схема реализации СКНФ в Simulink представлена на рисунке 5: 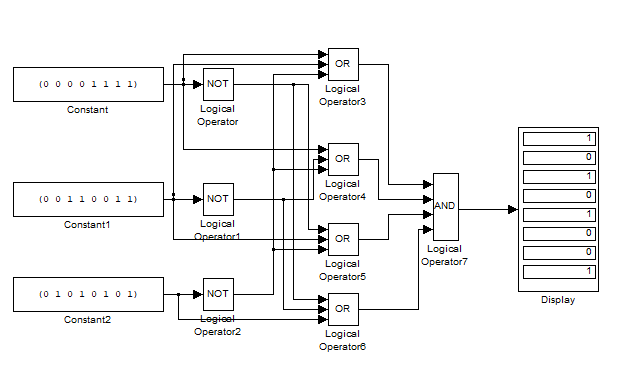 Рисунок 5 – Схема реализации СКНФ Задание 6. ВыводыСравнить таблицы истинности, полученные в п. 2 и п. 5. Сделать выводы. Как видно из полученных результатов таблицы истинности в заданиях 1 и 2 совпадают, что свидетельствует о корректности проведенных вычислений по логическим операциям |
