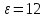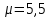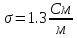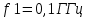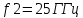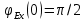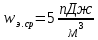Содержание задания
 Скачать 494.65 Kb. Скачать 494.65 Kb.
|
|
Московский Энергетический институт (технический университет) Институт радиотехники и электроники Кафедра Основ радиотехники Дисциплина: Электродинамика Типовой расчет Выполнил: Группа: Проверила: Москва, 2018 Содержание задания 1. Найдите тангенс угла потерь и угол потерь на частотах f1 и f2. 2. 2.Рассчитайте и постройте частотные зависимости коэффициента фазы, коэффициента ослабления, длины волны и фазовой скорости по точным формулам (жирная линия) в диапазоне частот, в котором тангенс угла потерь изменяется в пределах от 0.02 до 50. Используйте логарифмический масштаб по оси частот. На этих же графиках покажите кривые, полученные: а) по приближенным формулам для среды с малыми потерями (тонкая линия, в диапазоне, где tgδ=0,02..1); б) по приближенным формулам для хорошо проводящей (металлоподобной) среды (тонкая штриховая линия, в диапазоне, где tgδ=1..50). По графикам определите частотные области, в которых приближенные формулы дают погрешность не выше 5%. 3. Для частот f1, f2 и f3= 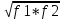 рассчитайте и сведите в таблицу значения коэффициента фазы, коэффициента ослабления, длины волны, модуля и фазы характеристического сопротивления среды. Получите общие формулы (для Вашего случая) и формулы с конкретными числовыми параметрами (на частотах f1, f2 и f3) для зависимостей комплексных амплитуд векторов E и H и плотности потока мощности от пространственной координаты и для зависимостей мгновенных значений векторов E и H от пространственной координаты и от времени. Для частот f1 и f2 рассчитайте и постройте зависимости амплитуды и мгновенных (при t = 0) значений проекций векторов E , H а также модуля вектора Пср от пространственной координаты распространения волны в пределах от 0 до 1,5λ. Примечание. Графики для амплитуды совместите с графиками для мгновенных значений. Для каждой частоты все графики приведите на одной странице один под другим в одинаковом масштабе по горизонтали. рассчитайте и сведите в таблицу значения коэффициента фазы, коэффициента ослабления, длины волны, модуля и фазы характеристического сопротивления среды. Получите общие формулы (для Вашего случая) и формулы с конкретными числовыми параметрами (на частотах f1, f2 и f3) для зависимостей комплексных амплитуд векторов E и H и плотности потока мощности от пространственной координаты и для зависимостей мгновенных значений векторов E и H от пространственной координаты и от времени. Для частот f1 и f2 рассчитайте и постройте зависимости амплитуды и мгновенных (при t = 0) значений проекций векторов E , H а также модуля вектора Пср от пространственной координаты распространения волны в пределах от 0 до 1,5λ. Примечание. Графики для амплитуды совместите с графиками для мгновенных значений. Для каждой частоты все графики приведите на одной странице один под другим в одинаковом масштабе по горизонтали.4. Проанализируйте полученные в пп. 1-3 результаты и представьте выводы: о влиянии частоты и tgδ на исследуемые характеристики и графики; о том, в каком направлении график для мгновенных значений H сдвинут относительно графика для E в пространстве и в каком направлении – во времени; обоснуйте, как затухание на расстоянии λ зависит от тангенса угла потерь. Ход работы Исходные данные:
1 ПУНКТ а) тангенс угла потерь для частоты 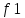 : :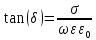 , где , где 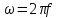 => => 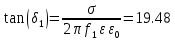 б) тангенс угла потерь для частоты 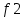 : :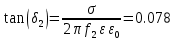 2 ПУНКТ Зададим диапазон частот, в котором тангенс угла потерь изменяется в пределах от 0.02 до 50: рад/c рад/c рад/c Запишем точные формулы для коэффициента фазы ( 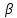 ), коэффициента ослабления ( ), коэффициента ослабления (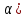 , длины волны (λ) и фазовой скорости (Vf): , длины волны (λ) и фазовой скорости (Vf):  Где Vsv =  м/c – скорость света м/c – скорость светаРассмотрим отдельно каждую из заданных сред: а) среда с малыми потерями 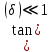 : :Запишем так же приближенные формулы:   Где Z0 = 377 Ом – характеристическое сопротивление вакуума   Найдём частотные области на графике, в которых приближенные формулы дают погрешность не выше 5%: б) хорошо проводящая среда 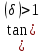 : :    Построим графики для полученных результатов: 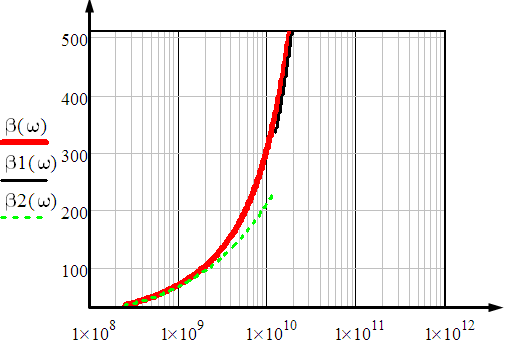 Рисунок 1 – график коэффициентов фазы  Рисунок 2 – погрешность коэффициентов фазы Частотные области с погрешностью до 5%: 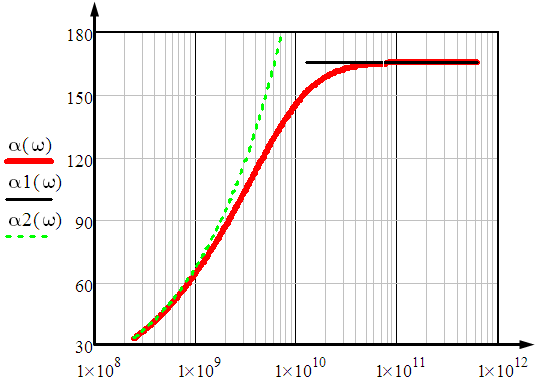 Рисунок 3 – график коэффициентов ослабления  Рисунок 4 – погрешность коэффициентов ослабления Частотные области с погрешностью до 5%: 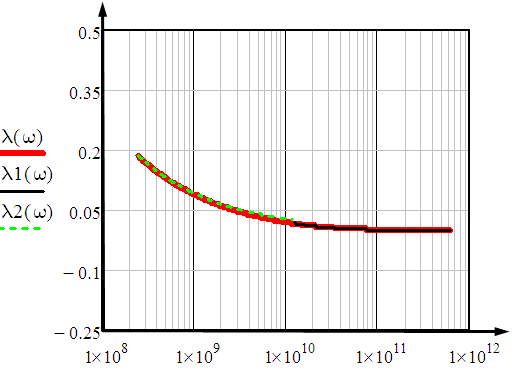 Рисунок 5 – график длин волн 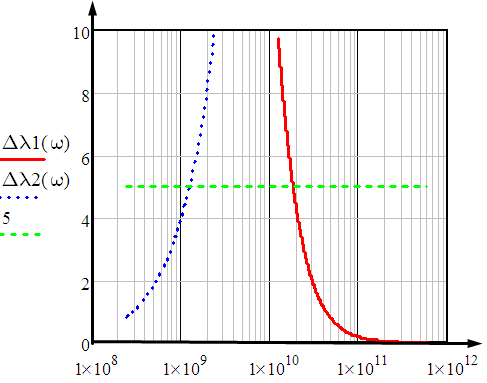 Рисунок 6 – погрешность длин волн Частотные области с погрешностью до 5%: 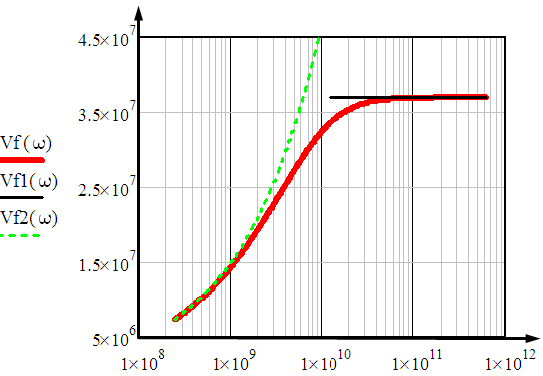 Рисунок 7 – график фазовых скоростей 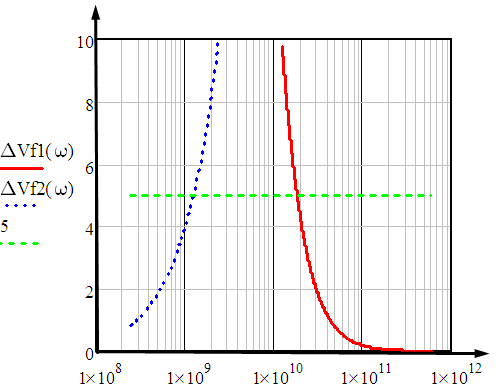 Рисунок 8 – погрешность фазовых скоростей Частотные области с погрешностью до 5%: 3 ПУНКТ               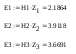  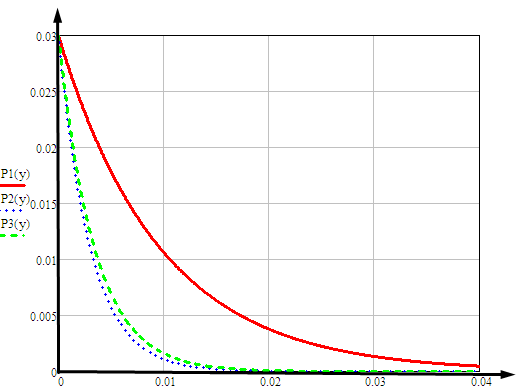 Рисунок 9 – среднее значение вектора Пойнтинга в плоскости x при частоте f1, f2, f3 Получить общие (для своего случая) формулы (на частотах f1, f2 и f3) для зависимостей мгновенных значений векторов E и H от пространственной координаты и от времени. 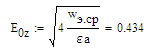 Для частот f1 и f2 рассчитать и построить зависимость амплитуды значений проекций векторов E, H от пространственной координаты распространения волны в пределах от 0 до 1.5λ. Для частот f1 и f2 рассчитать и построить зависимость мгновенных (при t=0) значений проекций векторов E, H от пространственной координаты распространения волны в пределах от 0 до 1.5λ. 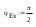 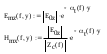 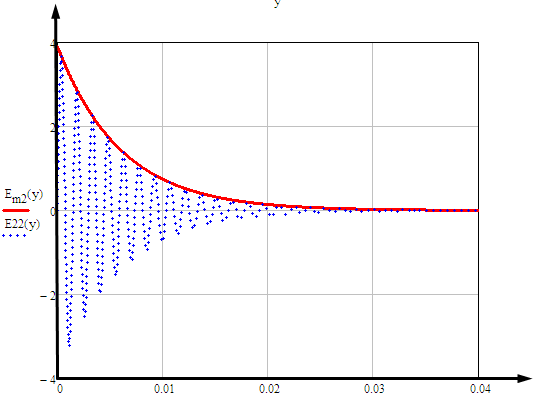 Графики амплитуды и мгновенного значений напряженности электрического поля при частоте f2 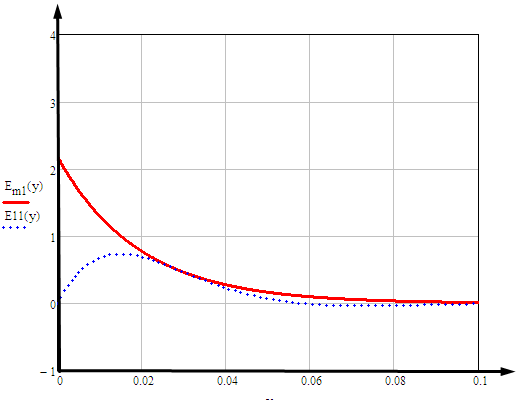 Графики амплитуды и мгновенного значений напряженности электрического поля при частоте f1  Графики амплитуды и мгновенного значений напряженности магнитного поля при частоте f2 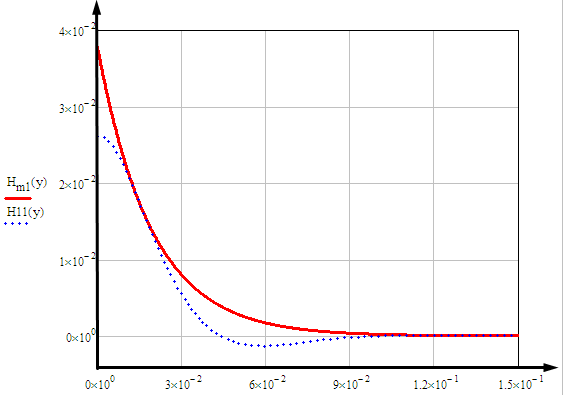 Графики амплитуды и мгновенного значений напряженности магнитного поля при частоте f1 4 ПУНКТ Проанализировав полученные результаты , выяснили , что при увеличении частоты (f) коэффициент фазы (β) нелинейно увеличивается , коэффициент затухания (α) возрастает , фазовая скорость (vф) увеличивается , а длинна волны (L) уменьшается. Тангенс угла потерь обратно пропорционален частоте волны, т. е. при увеличении частоты значение тангенса уменьшается, следовательно, уменьшается рассеяние энергии волны, следовательно, волна затухает медленнее. Соответственно при уменьшении тангенса угла диэлектрических потерь коэффициенты фазы, ослабления, длина волны и фазовая скорость ведут себя так же, как и при увеличении частоты. Амплитуды векторов Е, Н и Пср уменьшаются при увеличении пространственной координаты, вдоль которой распространяется электромагнитная волна. Из графиков проекций векторов Е(y) и Н(y) следует, что значения векторов в зависимости от координаты сдвинуты друг относительно друга на величину характеристического сопротивления φZc среды на данной частоте. Поскольку зависимость от времени обоих векторов Е и Н выражается в слагаемом ωt под знаком косинуса, зависимость сдвига по фазе от времени между этими векторами отсутствует. Также на каждой частоте скорость затухания колебаний для векторов Е и Н одинакова, поскольку они имеют один и тот же коэффициент затухания. |