Взаимодействие фотонного излучения с веществом
§1. Закон ослабления нерассеянного фотонного излучения. Коэффициенты ослабления
Фотонное косвенно ионизирующее излучение высокой энергии образуется:
при рассеянии (торможении) заряженных частиц (в основном электронов и позитронов) в кулоновском поле ядра – тормозное излучение; тормозное излучение имеет непрерывный спектр;
при радиоактивном распаде (при снятии возбуждённых состояний атомных ядер) и при аннигиляции частиц – гамма-излучение; гамма-излучение имеет линейчатый спектр;
при квантовых переходах на внутренних глубоколежащих электронных оболочках атомов – характеристическое излучение; характеристическое излучение имеет линейчатый спектр.
Выделяют также рентгеновское излучение – это фотонное излучение, состоящее из тормозного и характеристического излучений.
Взаимодействие фотонов с веществом определяется только их энергией ( Е ) и не зависит от происхождения фотонов.
П
Рис1. Прохождение узкого
параллельного пучка фотонов
через плоский слой.
рохождение излучения через вещество сопровождается рассеянием и поглощением его атомами вещества. Каждый акт взаимодействия кванта с атомами вещества приводит либо к полному исчезновению (поглощению), либо к существенному изменению направления его движения (рассеянию). Найдем закон ослабления узкого параллельного моноэнергетического пучка фотонов в плоской однородной мишени (рис.1), перпендикулярно поверхности которой падает поток квантов  . При этом предполагаем, что детектор регистрирует только то излучение (не рассеянное), которое не испытало взаимодействий с атомами вещества и имеет то же направление и энергию, что и излучение источника. Этот случай реализуется в так называемой «узкой» или «хорошей» геометрии измерений (рис.2). Коллиматор К1 находится между источником и поглотителем, формируя узкий мононаправленный пучок излучения, а коллиматор К2 между поглотителем и детектором отсекает рассеянную компоненту излучения. В узкой геометрии достаточно одного взаимодействия чтобы вывести фотон из первоначального параллельного пучка. Поэтому число квантов . При этом предполагаем, что детектор регистрирует только то излучение (не рассеянное), которое не испытало взаимодействий с атомами вещества и имеет то же направление и энергию, что и излучение источника. Этот случай реализуется в так называемой «узкой» или «хорошей» геометрии измерений (рис.2). Коллиматор К1 находится между источником и поглотителем, формируя узкий мононаправленный пучок излучения, а коллиматор К2 между поглотителем и детектором отсекает рассеянную компоненту излучения. В узкой геометрии достаточно одного взаимодействия чтобы вывести фотон из первоначального параллельного пучка. Поэтому число квантов  , выбывающих из пучка в тонком слое , выбывающих из пучка в тонком слое  , пропорционально толщине слоя , пропорционально толщине слоя  и количеству квантов и количеству квантов 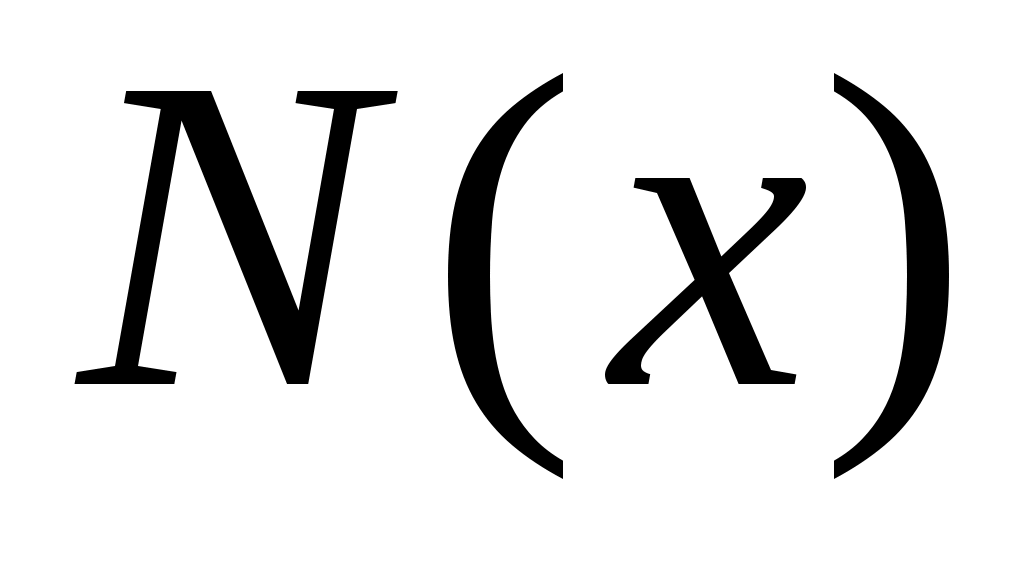 , дошедших до данной глубины , дошедших до данной глубины 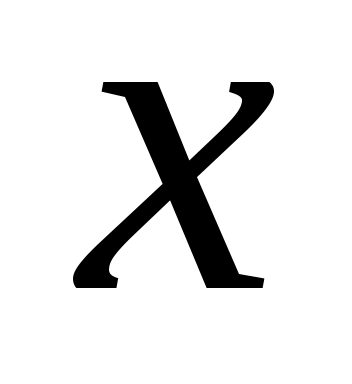 : :
 , (1) , (1)
где 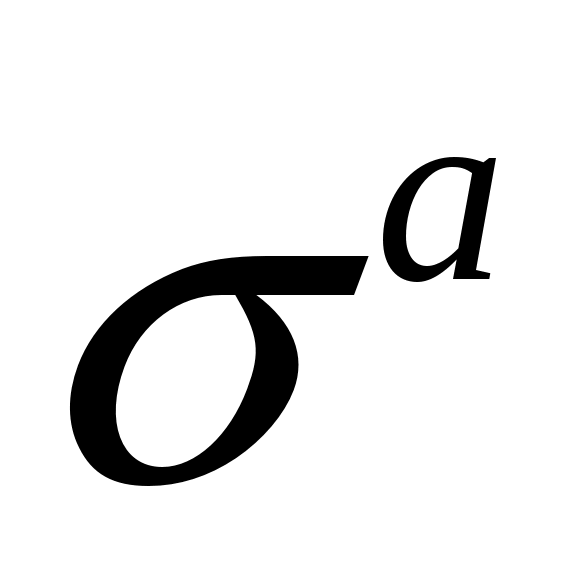 – коэффициент пропорциональности, представляющий вероятность рассеяния или поглощения кванта одним атомом, n – количество атомов в единице объёма. – коэффициент пропорциональности, представляющий вероятность рассеяния или поглощения кванта одним атомом, n – количество атомов в единице объёма.

Рис.2. Схема эксперимента в геометрии узкого пучка:
S – источник, П – поглотитель, Д – детектор, К – коллиматоры
Поскольку излучение монохроматическое и 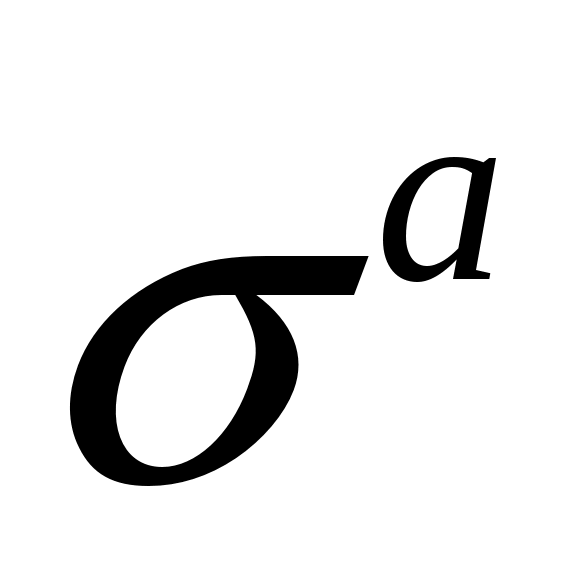 не зависит от глубины залегания слоя не зависит от глубины залегания слоя  то, разделяя переменные: то, разделяя переменные:
 (2) (2)
и интегрируя (2) с учетом того, что при  , получаем: , получаем:
 (3) (3)
Число остающихся в пучке квантов уменьшается экспоненциально с ростом толщины поглотителя. Напоминаем, что приведенный анализ предполагает геометрию ”узкого” пучка излучения, т.е. любой отклоненный фотон, как бы не был мал угол отклонения, считается полностью поглощенным, т.е. на детектор за поглотителем попасть не может.
Величину  называют макроскопическим сечением или линейным коэффициентом ослабления излучения, поскольку он определяет скорость убывания первичных (не рассеянных) фотонов из пучка. называют макроскопическим сечением или линейным коэффициентом ослабления излучения, поскольку он определяет скорость убывания первичных (не рассеянных) фотонов из пучка.
Из уравнения (2), которое можно записать в виде:

следует, что линейный коэффициент ослабления имеет размерность  и численно равен доле моноэнергетических квантов, выбывающих из параллельного пучка, т.е. испытавших столкновение, на единице пути излучения в веществе. и численно равен доле моноэнергетических квантов, выбывающих из параллельного пучка, т.е. испытавших столкновение, на единице пути излучения в веществе.
Величину  , где , где  – плотность вещества мишени, называют массовым коэффициентом ослабления. Толщину слоя в этом случае необходимо задавать в единицах массы, приходящейся на 1 – плотность вещества мишени, называют массовым коэффициентом ослабления. Толщину слоя в этом случае необходимо задавать в единицах массы, приходящейся на 1 поверхности мишени – поверхности мишени – 
 (4) (4)
Размерность массового коэффициента –  . .
Линейный коэффициент ослабления  зависит от энергии фотонов зависит от энергии фотонов , плотности , плотности  и порядкового номера вещества Z: и порядкового номера вещества Z:

Массовый коэффициент ослабления зависит только от Z и 

Вещества с одинаковыми эффективными порядковыми номерами имеют равные массовые коэффициенты ослабления. Так, массовые коэффициенты ослабления воды, кислорода, азота, воздуха, углерода и живой ткани почти совпадают, т.к. их эффективные порядковые номера не сильно отличаются.
Коэффициент 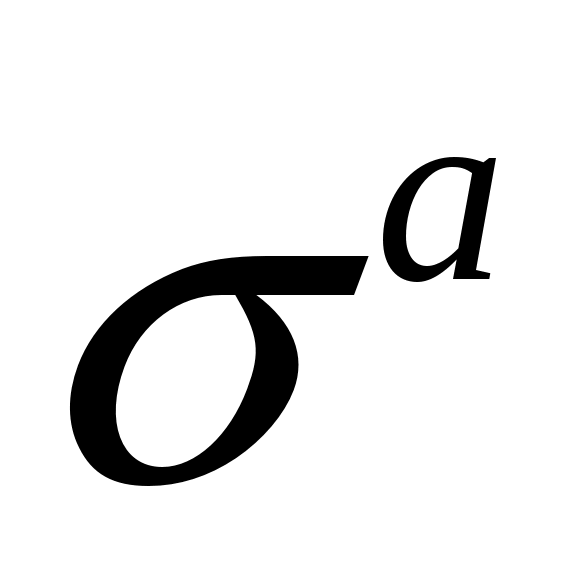 называют полным микроскопическим сечением или, иногда, атомным коэффициентом ослабления, характеризующим вероятность для фотона испытать взаимодействие в мишени с одним атомом на 1 см2. Толщину в этом случае нужно задавать как в формуле (3) числом атомов на 1 называют полным микроскопическим сечением или, иногда, атомным коэффициентом ослабления, характеризующим вероятность для фотона испытать взаимодействие в мишени с одним атомом на 1 см2. Толщину в этом случае нужно задавать как в формуле (3) числом атомов на 1  – –  . Размерность . Размерность  – см2/атом, единицей измерения является барн; 1барн/атом = 10-24 см2/атом. Используется и коэффициент ослабления на электрон – – см2/атом, единицей измерения является барн; 1барн/атом = 10-24 см2/атом. Используется и коэффициент ослабления на электрон –  см2/электрон. Очевидно, что: см2/электрон. Очевидно, что:  (5) (5)
Cвязь между различными коэффициентами легко найти, если учесть, что число атомов единице объёма равно  , а число электронов – , а число электронов –  , где , где  – число Авогадро и – число Авогадро и  – атомный вес: – атомный вес:
 (6) (6)
 (7) (7)
 (8) (8)
 (9) (9)
Величина  называется средней длиной свободного пробега фотонов в веществе до cоударения. Действительно, называется средней длиной свободного пробега фотонов в веществе до cоударения. Действительно,  – вероятность для кванта пройти путь – вероятность для кванта пройти путь 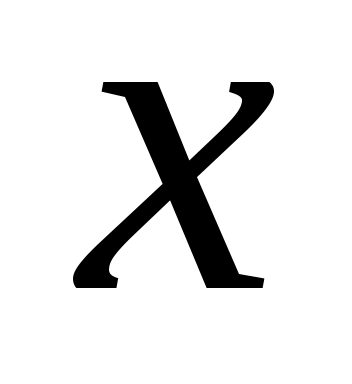 без соударения. Тогда по определению средний путь будет равен: без соударения. Тогда по определению средний путь будет равен:

Из формул (3) и (4) следует, что поток фотонов ослабляется в е=2,718 раз на пути, равном длине свободного пробега.
Величины  или или  характеризуют путь фотона в веществе в длинах свободного пробега. характеризуют путь фотона в веществе в длинах свободного пробега.
Толщину слоя поглотителя, уменьшающую поток фотонов вдвое, называют слоем половинного ослабления  или или  . Полагая в формулах (3) и (4) . Полагая в формулах (3) и (4)  при при  или или  , получаем: , получаем:
 и и  (10) (10)
Слой половинного ослабления характеризует поглощающую способность материала для излучения определенной энергии. Длина свободного пробега и слой половинного ослабления связаны соотношениями:

Для химического соединения или однородной смеси элементов массовые коэффициенты ослабления определяются по формуле:
 , (11) , (11)
где  – массовый коэффициент ослабления i-гo элемента, входящего в смесь; – массовый коэффициент ослабления i-гo элемента, входящего в смесь;  – весовая доля i-гo элемента в смеси или соединении. – весовая доля i-гo элемента в смеси или соединении.
Практически в диапазоне энергий радиоактивных препаратов (десятки КэВ – 3 МэВ) имеют место в основном три процесса взаимодействия фотонов с веществом, приводящие к удалению фотонов из первичного пучка.
1.Фотоэлектрический эффект, при котором фотон передает всю свою энергию связанному электрону, причём часть энергии расходуется на преодоление связи электрона с атомом, а остальная часть на сообщение электрону кинетической энергии. Этот эффект является преобладающим при низких энергиях.
2.Рассеянние атомными электронами, в результате которого фотон отклоняется от своего первоначального направления. При низких энергиях, когда длина волны сравнима с размерами атома, имеет место когерентное или томсон-рэлеевское рассеяние, при котором энергия фотона не изменяется. При энергиях, несколько превышающих энергию связи электронов, рассеяние не когерентно и некоторая доля энергии фотона передается электрону. Эта доля зависит от энергии и импульса электрона внутри атома. При энергиях, значительно превышающих энергию связи электронов, кванты рассеиваются так, как если бы электроны были свободными и покоились. Это комптоновское рассеяние или комптон-эффект, который в области энергий квантов около 1МэВ является преобладающим видом взаимодействия.
3.Образование пар, при котором фотоны в поле ядра или электрона исчезают и рождается пара электрон-позитрон, полная кинетическая энергия которой равна энергии фотона за вычетом энергии покоя двух появившихся частиц. Этот процесс может происходить только в том случае, когда энергия фотона равна или превышает энергию пары электрон-позитрон. Он становится преобладающим видом взаимодействия при больших энергиях.
Так как эти три процесса происходят независимо друг от друга, полный коэффициент ослабления и полное сечение взаимодействия можно разделить на три части, характеризующие вероятность каждого из процессов. Уравнение (1) и полные сечения взаимодействия можно записать в виде:
 , ,  (12) (12)

 (13) (13)

Здесь индексами ф , к и п помечены части, относящиеся соответственно к фотоэффекту, комптон-эффекту и эффекту рождения пар.
В результате указанных взаимодействий часть поглощенной энергии исходного кванта передается фотонам (рассеянным фотонам, фотонам флюоресценции, аннигиляционным фотонам), а другая часть передается частицам. Последняя часть называется истинным поглощением. В ряде практических приложений (биологические эффекты, воздействие радиации на материалы, защита и пр.) надо знать истинное поглощение электромагнитного излучения. Поэтому в упомянутых выше процессах (кроме когерентного рассеяния) коэффициенты могут быть представлены в виде:
 
где индекс а указывает на истинное поглощение, а индекс s – на рассеяние.
§2. Процессы взаимодействия фотонов с веществом
Фотоэффект – это чисто квантовое явление. Он невозможен на свободном электроне, т.к. законы сохранения энергии и импульса требуют участия в этом взаимодействии третьего тела. При атомном фотоэффекте первичный фотон поглощается и передает всю свою энергию одному из атомных электронов, выбивая его из атома.
Из закона сохранения энергии кинетическая энергия фотоэлектрона:
 , (14) , (14)
где  – ионизационный потенциал соответствующей оболочки,  – энергия отдачи ядра. Энергия отдачи ядра обычно мала и ею можно пренебречь. Угловое распределение фотоэлектронов относительно направления полета кванта зависит от их энергии. При малой энергии (десятки КэВ) фотоэлектроны испускаются преимущественно перпендикулярно направлению распространения квантов. С ростом энергии угол вылета уменьшается (20° – 30° при энергиях 0,5 МэВ), но никогда фотоэлектроны не испускаются в направлении движения кванта. После испускания фотоэлектрона атом ионизован и находится в возбуждённом состоянии. Возбуждение снимается одним из следующих способов: а) радиационный переход – свободное место электрона на i-уровне заполняет электрон с более высокого уровня j и при этом испускается фотон характеристического излучения, энергия которого равна: E = h ij = I i-I j ; б) безрадиационный переход – свободное место электрона на i-уровне заполняет электрон с более удалённого уровня j и при этом с одного из внешних уровней испускается электрон ( Оже-электрон). Этот переход называют оже-эффектом. Оже-электроны с большей вероятностью наблюдаются на атомах с малыми и средними значениями Z. Кванты характеристического излучения поглощаются на расстояниях того же порядка, что и пробег фотоэлектронов. Поэтому в случае фотоэффекта величина  пренебрежимо мала и  . Угловое распределение характеристического излучения и оже-электронов изотропно. Фотоэлектроны могут быть выбиты из любой оболочки атома, если энергия фотона больше энергии связи электрона на этой оболочке. Поэтому сечение фотоэффекта претерпевает резкие скачки при энергиях, равных энергиям ионизации оболочек. Вероятность фотоэффекта быстро растет с увеличением энергии связи электрона, так что при энергиях, превышающих энергию связи К-оболочки, поглощение во внешних оболочках ничтожно и в 80% случаев фотоэффект идет на К-оболочке. При энергиях  (но не вблизи края К-поглощения):  (15)  (16)  (17) При дальнейшем увеличении  сечение уменьшается несколько медленнее, чем  и при высоких энергиях (  ) пропорционально  . По этой причине для тяжелых элементов (свинца, например) фотоэффект имеет заметное значение даже при энергиях около 5 МэВ. Из последних формул следует, что сечение фотоэффекта Z 5 и быстро убывает с увеличением энергии первичного фотона. Поэтому этот эффект взаимодействия фотонов играет существенную роль в веществах с большим Z и при небольших энергиях фотонов. Фотоэффект – основной процесс в алюминии (Z= 13) при Е < 0,05 МэВ, а в свинце (Z=82) – при Е < 0,5 МэВ. Х

Рис. 3. Зависимость сечения
фотоэффекта
от энергии фотона.
арактер зависимости сечения фотоэффекта от энергии фотона показан на рис.3. С уменьшением энергии фотона сечение фотоэффекта растёт до тех пор, пока энергия фотона не станет равной потенциалу ионизации для К-оболочки (E =I к). При дальнейшем уменьшении энергии фотона фотоэффект на К-оболочке становится невозможен, и на кривой будет наблюдаться резкий вертикальный скачок, называемый К-скачком поглощения. Край К-полосы поглощения можно оценить из закона Мозли:  , где  – постоянная Ридберга. При дальнейшем уменьшении энергии фотона вероятность фотоэффекта снова начинает расти. Рост прекращается при Е =I L, где наблюдается новый скачок сечения, связанный с поглощением на L-оболочке, и т.д.
Комптон-эффект идет главным образом на слабо связанных электронах внешних оболочек атомов. Если энергия фотонов существенно превышает энергию связи этих электронов, последние можно считать свободными и рассматривать процесс как упругое столкновение двух шариков с массами  и и  (рис.4). (рис.4).
Применение релятивистских законов сохранения энергии и импульса в предположении первоначально покоившегося электрона приводит к уравнениям:
 
Здесь  – скорость электрона в – скорость электрона в
единицах скорости света
Исключая из этих уравнений
Рис.4. Схема комптон-эффекта любые две из величин  , ,  или или  , получим выражения для энергий рассеянного фотона , получим выражения для энергий рассеянного фотона  , электрона отдачи , электрона отдачи  и связи углов и связи углов  и и  : :

(18)
(19)
(20)
Угол рассеяния фотонов  может изменяться от 0 до 180°, а угол может изменяться от 0 до 180°, а угол  , под которым отлетает электрон отдачи – от 0 до 90°. Энергия комптон-электронов может иметь значения от нуля до максимально возможной величины: , под которым отлетает электрон отдачи – от 0 до 90°. Энергия комптон-электронов может иметь значения от нуля до максимально возможной величины:
 , (21) , (21)
а энергия фотонов – от  до минимально возможной величины, соответствующей рассеянию на угол до минимально возможной величины, соответствующей рассеянию на угол  =180°: =180°:
 (22) (22)
Отсюда следует, что рассеянные назад кванты всегда имеют энергию  независимо от начальной энергии, а энергия фотона, рассеянного под углом 900, не превышает 0,511 МэВ. Чем больше энергия рассеянного фотона, тем меньше угол рассеяния и энергия, переданная электрону. Чем больше угол рассеяния, тем больше энергия электрона и тем ближе его направление движения к направлению первичного фотона. независимо от начальной энергии, а энергия фотона, рассеянного под углом 900, не превышает 0,511 МэВ. Чем больше энергия рассеянного фотона, тем меньше угол рассеяния и энергия, переданная электрону. Чем больше угол рассеяния, тем больше энергия электрона и тем ближе его направление движения к направлению первичного фотона.
Вероятность для фотона испытать комптоновское рассеяние в любой мишени зависит только от количества электронов, содержащихся в этой мишени. Электронное сечение комптоновского рассеяния  не зависит от материала мишени. Следовательно, согласно формулам (6) и (7): не зависит от материала мишени. Следовательно, согласно формулам (6) и (7):
 (23) (23)
 (24) (24)
Поскольку  меняется от 0,5 для легких элементов до 0,4 для самых тяжелых, массовый коэффициент ослабления за счет комптон-эффекта мало зависит от материала поглотителя, а линейный коэффициент примерно пропорционален плотности поглотителя. меняется от 0,5 для легких элементов до 0,4 для самых тяжелых, массовый коэффициент ослабления за счет комптон-эффекта мало зависит от материала поглотителя, а линейный коэффициент примерно пропорционален плотности поглотителя.
Сечение комптон-эффекта сложным образом зависит от энергии фотонов, убывая с ростом энергии приблизительно как  (рис.5). Комптоновское рассеяние является основным процессом взаимодействия фотонов в области энергий (0,0515) МэВ для Al и (0,55) МэВ для Pb. (рис.5). Комптоновское рассеяние является основным процессом взаимодействия фотонов в области энергий (0,0515) МэВ для Al и (0,55) МэВ для Pb.
П

Рис.5. Зависимость сечения комптоновского рассеяния от энергии фотона
ри малых энергиях первичный квант почти полностью передает свою энергию рассеянному кванту и лишь малую долю – электронам отдачи. Коэффициент истинного поглощения  мал. С ростом энергии доля энергии, передаваемая электрону, растет. Средние значения этой энергии приведены в таблице 1. В области энергий от 0,25 МэВ до З МэВ мал. С ростом энергии доля энергии, передаваемая электрону, растет. Средние значения этой энергии приведены в таблице 1. В области энергий от 0,25 МэВ до З МэВ  остается практически постоянным, что имеет существенное значение при измерениях с помощью ионизационных детекторов. остается практически постоянным, что имеет существенное значение при измерениях с помощью ионизационных детекторов.
Таблица 1
Средние энергии вторичных фотонов и электронов
после комптоновского рассеяния
-
E , МэВ
|
E, МэВ
|
Te , МэВ
|
0,01
|
0,0098
|
0,0002
|
1,0
|
0,56
|
0,44
|
10
|
3,16
|
6,84
|
Отметим, что при комптоновских столкновениях электроны атома участвуют в рассеянии независимо друг от друга и рассеянное комптоновское излучение является некогерентным. Полная интенсивность некогерентного излучения равна сумме интенсивностей излучений от отдельных электронов. Таким образом, сечение эффекта Комптона на атоме в Z раз больше соответствующего сечения на электроне.
В области низких энергий E и при больших Z, когда существенен эффект связи электронов в атоме, наблюдается максимум рэлеевского (когерентного) рассеяния фотонов всей совокупностью атомных электронов (всей электронной оболочкой). При рэлеевском рассеянии энергия отдачи воспринимается атомом как целым. При рэлеевском рассеянии атом не ионизируется и не возбуждается, а фотон рассеивается без изменения своей энергии. Рассеяние происходит в основном на малые углы, т.е. рассеянное излучение направленно преимущественно вперёд. Полное сечение когерентного рассеяния на один атом имеет вид:
 . .
Сечение когерентного рассеяния при больших Z и малых Е значительно превышает сечение комптоновского рассеяния (таблица 2). Однако при этих Z и энергиях сечение фотоэффекта много больше кг и поэтому когерентное рассеяние практически не влияет на процесс ослабления фотонов, хотя именно оно определяет характер и существование рассеянного излучения.
Таблица 2
Вклад в % когерентногo рассеяния в общее сечение рассеяния фотонов
Вещество
|
 ,МэВ ,МэВ
|
0,01
|
0,1
|
1
|
5
|
10
|
Al
|
83,5
|
8,7
|
0,2
|
----
|
----
|
Cu
|
95
|
25,4
|
0,8
|
0,09
|
----
|
Pb
|
99,1
|
66,1
|
4,2
|
0,47
|
0,2
|
Образование электронно-позитронных пар – это типично квантовый процесс. Он происходит в сильном электрическом поле ядра, при этом первичный фотон превращается в электрон-позитронную пару, которой передается почти вся энергия фотона Е. Некоторую энергию отдачи получает ядро атома, но благодаря большой массе ядра эта энергия отдачи невелика (обычно менее 5 кэВ). Закон сохранения энергии для этого процесса имеет вид:
 , (25) , (25)
где  и и  – кинетические энергии электрона и позитрона, – кинетические энергии электрона и позитрона,  – энергия отдачи ядра. Из (25) следует, что эффект образования пар – пороговый процесс. Если пренебречь энергией отдачи ядра, то энергия первичного фотона Е должна быть не менее m+c2 + mc2 = 1,022 МэВ. В вакууме фотон не может образовать пару электрон-позитрон, так как в данном случае нарушается закон сохранения импульса. – энергия отдачи ядра. Из (25) следует, что эффект образования пар – пороговый процесс. Если пренебречь энергией отдачи ядра, то энергия первичного фотона Е должна быть не менее m+c2 + mc2 = 1,022 МэВ. В вакууме фотон не может образовать пару электрон-позитрон, так как в данном случае нарушается закон сохранения импульса.
Энергия фотона распределяется почти равновероятно между электроном и позитроном, т.е. и те и другие имеют широкий энергетический спектр от нулевой энергии до максимально возможной ( - - ). ).
Д

Рис. 6 Дифференциальная вероятность образования пар: V = (T+ meC2) E, цифры у кривых - энергии фотонов в МэВ.
Рис.6. Дифференциальное по энергии Т+ сечение образования пар
(по оси абсцисс отложено T+/Еγ-2m0c2,
цифры у кривых – энергия фотонов в МэВ)
ифференциальное по энергии позитрона (T+) сечение образования пар для различных энергий Е приведено на рисунке 6. При больших энергиях фотонов ( ) электрон и позитрон испускаются под малым углом относительно направления движения кванта – средний угол порядка ) электрон и позитрон испускаются под малым углом относительно направления движения кванта – средний угол порядка  . При малых энергиях фотонов углы разлета комптоновской пары могут быть очень большими (20° – 60°), особенно в случае ядер с большими . При малых энергиях фотонов углы разлета комптоновской пары могут быть очень большими (20° – 60°), особенно в случае ядер с большими  . .
Образование пар может происходить и в поле атомного электрона. При этом энергия отдачи электрона много больше энергии отдачи ядра, поэтому пороговая энергия фотона в этом случае выше 4m0c2. Сечение образования пар в поле ядра много больше, чем в электрическом поле электрона. Относительный вклад рождения пар в поле электронов приводится в таблице 3.
Таблица 3
Вклад (в%) рождения пар в поле электронов
в общее сечение рождения пар
Вещество
|
 ,МэВ ,МэВ
|
3
|
10
|
100
|
Al
|
0,6
|
4
|
6,9
|
Cu
|
0,27
|
1,9
|
3,2
|
Pb
|
0,08
|
0,8
|
1,3
|
Полное сечение образования пар сильно зависит от заряда ядра
и сложным образом зависит от  . Вначале оно быстро растет с ростом энергии фотонов, затем рост замедляется и при очень больших энергиях сечение стремится к постоянной величине, не зависящей от энергии. Характер этой зависимости показан на рис.7. . Вначале оно быстро растет с ростом энергии фотонов, затем рост замедляется и при очень больших энергиях сечение стремится к постоянной величине, не зависящей от энергии. Характер этой зависимости показан на рис.7.


Рис.7. Зависимость сечения образования пар от энергии фотона
(26)
Эффект рождения пар является основным процессом взаимодействия фотонов с веществом при больших энергиях, например, в Al при E15 МэВ, в Pb при E5 МэВ.
В процессе образования пар часть энергии первичного фотона Е материализуется в виде позитрона и электрона. Но позитрон в конечном счёте обязательно аннигилирует с образованием двух гамма-квантов. Этот процесс происходит, в основном, в конце пробега позитрона, когда его кинетическая энергия Т 0. При этом образуются два аннигиляционных гамма-кванта, энергии которых равны (примерно) m 0c2 = 0,511 МэВ и они летят в противоположных направлениях. Это следует из закона сохранения импульса. Угловое распределение рождающихся электрона и позитрона можно считать изотропным в пределах 4 стерадиан. Процесс аннигиляции необходимо учитывать при расчете ослабления высокоэнергетических фотонов, т.к. вторичные аннигиляционные кванты дают вклад в поток рассеянного излучения.
По известным сечениям или коэффициентам ослабления в каком – либо веществе можно оценить их значения для другого вещества. Например, для перехода от коэффициентов ослабления в свинце к коэффициентам для другого вещества с порядковым номером, атомной массой и плотностью соответственно и и  следует пользоваться формулами: следует пользоваться формулами:
 (27) (27)
 (28) (28)
 (29) (29)
В области малых энергий фотонов основной вклад в полный коэффициент ослабления вносит фотопоглощение. С увеличением энергии коэффициент ослабления уменьшается из-за быстрого уменьшения сечения фотоэффекта ( ) и более медленного уменьшения сечения комптон-эффекта ( ) и более медленного уменьшения сечения комптон-эффекта ( ). При дальнейшем росте энергии все больший вклад вносит эффект рождения пар и коэффициент ослабления начинает увеличиваться, стремясь при больших энергиях к постоянной величине, определяемой только этим эффектом. Кроме того, при больших энергиях нужно учитывать вклад ядерных процессов. ). При дальнейшем росте энергии все больший вклад вносит эффект рождения пар и коэффициент ослабления начинает увеличиваться, стремясь при больших энергиях к постоянной величине, определяемой только этим эффектом. Кроме того, при больших энергиях нужно учитывать вклад ядерных процессов.
В таблице 4 приведены области энергий, в которых преобладает тот или иной процесс взаимодействия фотонов с веществом.
Таблица 4.
Погло-
титель
|
Z
|
A
|
Область, в которой процесс преобладает, кэВ
|
Фотоэффект
|
Комптон-эффект
|
Образование пар
|
Воздух
|
7
|
14
|
20
|
30 – 23103
|
23103
|
Al
|
13
|
27
|
50
|
50 – 15103
|
15103
|
Cu
|
29
|
64
|
150
|
150 – 10103
|
10103
|
Pb
|
82
|
207
|
500
|
500 – 5103
|
5103
|
Таким образом, на зависимости коэффициента ослабления от  имеется минимум. В алюминии он наблюдается при энергии примерно 20 МэВ ( имеется минимум. В алюминии он наблюдается при энергии примерно 20 МэВ (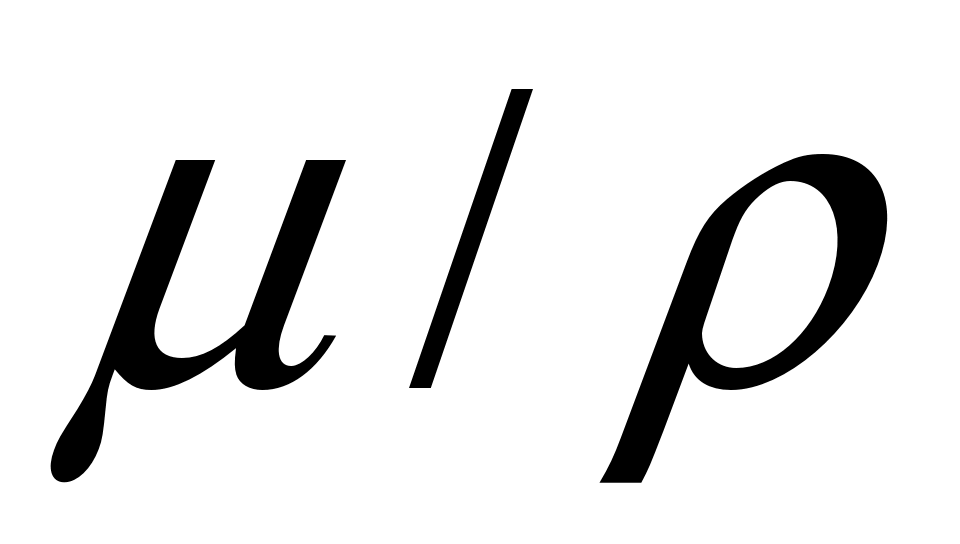 = 0,0217 = 0,0217 ), в меди при энергии 8 МэВ ( ), в меди при энергии 8 МэВ (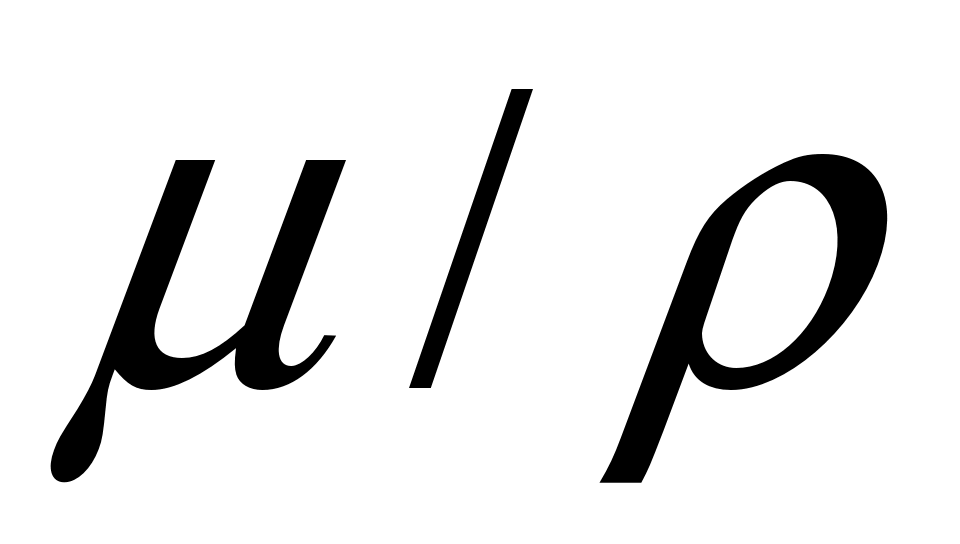 = 0,0306 = 0,0306  ) и в свинце при энергии 3,4 МэВ ( ) и в свинце при энергии 3,4 МэВ (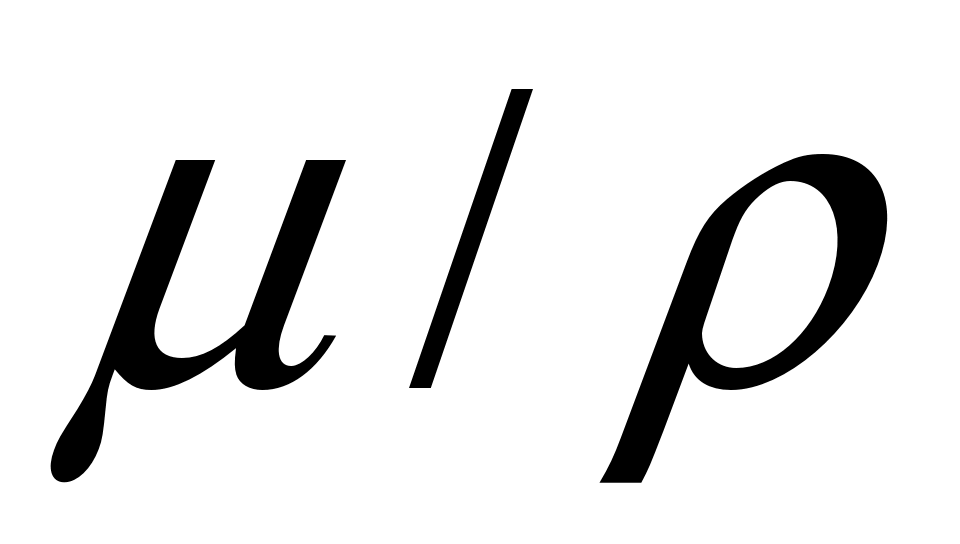 = 0,041 = 0,041  ). Для не слишком тяжелых элементов имеется область энергий ( примерно от 200 кэВ до 3 МэВ для А1, от 600 кэВ до 2 МэВ для Cu), когда фотоэффект еще мал, а эффект рождения пар еще несущественен, и ослабление излучения обусловлено практически только комптоновским рассеянием. В этой области массовые коэффициенты ослабления для различных веществ почти одинаковы, так как ). Для не слишком тяжелых элементов имеется область энергий ( примерно от 200 кэВ до 3 МэВ для А1, от 600 кэВ до 2 МэВ для Cu), когда фотоэффект еще мал, а эффект рождения пар еще несущественен, и ослабление излучения обусловлено практически только комптоновским рассеянием. В этой области массовые коэффициенты ослабления для различных веществ почти одинаковы, так как  . .
На рис.8 приведены полные и парциальные массовые коэффициенты ослабления и поглощения в свинце. На рис.13. приведена зависимость толщины слоя половинного ослабления от энергии фотонов в некоторых материалов.

Энергия фотонов, МэВ
Рис. 8. Коэффициенты поглощения и ослабления фотонов в свинце:
1,8 – фотоэффект, 2 – скачок К-поглощения, 3 – полное ослабление, 4 – полное поглощение, 5 – эффект рождения пар, 6 –комптоновское поглощение, 7 – комптоновское рассеяние, 9 – рэлеевское рассеяние
§3. Метод поглощения
Зависимость коэффициентов ослабления от энергии фотонов для различных материалов известна с погрешностью примерно (1-2)%. Это даёт возможность по экспериментально найденному коэффициенту ослабления найти энергию фотонов, если только известно, с какой стороны минимума кривой  лежит энергия исследуемого излучения. Это можно установить путем измерения лежит энергия исследуемого излучения. Это можно установить путем измерения  для двух различных веществ. Излучение большинства -источников попадает в область меньших энергий относительно минимума кривой для двух различных веществ. Излучение большинства -источников попадает в область меньших энергий относительно минимума кривой  . .
Если исследуемое излучение монохроматическое и если принять, что рассеянное излучение не попадает в детектор, то кривая ослабления (ее еще называют функцией пропускания) описывается уравнением (4). Строя ее в полулогарифмическом масштабе:
 , (30) , (30)
получаем прямую линию, тангенс угла наклона которой равен искомому коэффициенту ослабления (линейному, если толщина мишени отложена
в  или массовому, если в или массовому, если в  ). Наклон функции пропускания можно измерить с большой точностью, а погрешность определения энергии будет зависеть от того, насколько велика производная ). Наклон функции пропускания можно измерить с большой точностью, а погрешность определения энергии будет зависеть от того, насколько велика производная  . Если найденная величина . Если найденная величина  лежит в близи минимума функции лежит в близи минимума функции  , то погрешность определения , то погрешность определения  будет велика. В этом случае нужно в качестве поглотителей использовать легкие вещества, для которых этот максимум смещен в область высоких энергий. будет велика. В этом случае нужно в качестве поглотителей использовать легкие вещества, для которых этот максимум смещен в область высоких энергий.
Существенным источником погрешностей при определении энергии -квантов по функциям пропускания может быть недостаточно хорошая геометрия опыта, при которой в детектор может попадать часть рассеянного излучения. Чтобы уменьшить возможность его попадания необходимо:
Использовать по возможности узкий пучок -излучения; для этого источник коллимируется.
Расстояние источник – детектор брать по возможности большим.
Поглотитель располагать дальше от детектора с тем, чтобы из облучаемой области поглотителя детектор был виден под малым телесным углом.
Использовать детектор малых размеров, либо перед детектором использовать коллиматор.
Для уменьшения влияния излучения, рассеянного от окружающих предметов, а так же фонового излучения, как детектор, так и сам источник необходимо помещать в свинцовую защиту.
С целью уменьшения рассеяния в самом источнике должны применяться источники малого размера с высокой удельной активностью.
При большой толщине слоя поглотителя накапливается мягкое излучение, возникающее за счет многократного рассеяния -квантов в поглотителе. Эти рассеянные кванты могут попадать в детектор даже при хорошей коллимации. Поэтому толщина слоя поглотителя не должна сильно превышать среднюю длину свободного пробега -кванта  . .

Энергия гамма-излучения, МэВ
Рис.13. Толщина слоя половинного ослабления гамма-излучения
При исследовании кривых пропускания для мягкого излучения, особенно в материалах с большими  , особую трудность вызывает необходимость учета когерентного рассеяния. Сечение этого рассеяния в данном случае велико, а угол рассеяния очень мал. Поэтому полностью удалить из пучка когерентно рассеянные кванты коллимацией пучка практически невозможно. , особую трудность вызывает необходимость учета когерентного рассеяния. Сечение этого рассеяния в данном случае велико, а угол рассеяния очень мал. Поэтому полностью удалить из пучка когерентно рассеянные кванты коллимацией пучка практически невозможно.
Когда источник испускает -кванты нескольких различных энергий функция пропускания в полулогарифмическом масштабе уже не будет представлять собой прямую линию. Если при этом в спектре источника содержится две, максимум три не слишком близких друг к другу линии и если при больших толщинах поглотителя кривая переходит в прямую линию, тогда возможно приближенно определить коэффициенты ослабления для каждой компоненты излучения. Пример такой обработки показан на рис.14.
Кривая  описывает ослабление -излучения источника, испускающего кванты двух различных энергий – 2 МэВ и 1,5 МэВ, коэффициенты ослабления для которых отличаются в три раза ( описывает ослабление -излучения источника, испускающего кванты двух различных энергий – 2 МэВ и 1,5 МэВ, коэффициенты ослабления для которых отличаются в три раза ( ). Экстраполируя эту кривую в области больших толщин прямой линией (пунктир), получаем зависимость ). Экстраполируя эту кривую в области больших толщин прямой линией (пунктир), получаем зависимость  , описывающую ослабление потока квантов с большей энергией. Вычитая из экспериментальной кривой , описывающую ослабление потока квантов с большей энергией. Вычитая из экспериментальной кривой  значения, задаваемые пунктирной линией, получаем кривую ослабления значения, задаваемые пунктирной линией, получаем кривую ослабления  для квантов с меньшей энергией. В этом случае результаты менее точны по сравнению со случаем монохроматического пучка. Точность измерений можно повысить, если использовать детектор, способный регистрировать только кванты с наибольшей энергией, например, сцинтилляционный счетчик с амплитудным дискриминатором. для квантов с меньшей энергией. В этом случае результаты менее точны по сравнению со случаем монохроматического пучка. Точность измерений можно повысить, если использовать детектор, способный регистрировать только кванты с наибольшей энергией, например, сцинтилляционный счетчик с амплитудным дискриминатором.

Рис. 14. Пример обработки
кривой ослабления для -излучения с двумя линиями в спектре.
|
 Скачать 2.23 Mb.
Скачать 2.23 Mb.


 .
. 





 (4)
(4)
 (7)
(7) (8)
(8) (9)
(9)

 (10)
(10)

 (13)
(13)

 (15)
(15) (16)
(16) (17)
(17)



 , (21)
, (21) (22)
(22) (24)
(24)