Закон ослабления нерассеянного фотонного излучения. Коэффициенты ослабления

• Название: Закон ослабления нерассеянного фотонного излучения. Коэффициенты ослабления
• Дата: 14.07.2022
• Размер: 2.23 Mb.
• Имя файла: zadanie6-7.doc
• Тип: Закон; #630818
• страница: 2 из 3

§4. Факторы накопления фотонного излучения

Поле фотонного излучения в реальных задачах определяется не только не рассеянным излучением источника, но и рассеянными фотонами, которые испытали однократное или многократное (2 и более) взаимодействий в воздухе или материале поглотителя. Кроме этого, в детектор попадает также вторичное излучение: аннигиляционное, характеристическое, тормозное. Геометрию, при которой детектор регистрирует не рассеянное (первичное), рассеянное излучения, а также вторичное излучение, называют геометрией широкого пучка или "плохой" геометрией (рис.15).

Выражения (3) и (4) очень удобны для расчета ослабления излучения в веществе. Чтобы сохранить простоту записи и при этом учесть рассеянное излучение поступают следующим образом. Рассеянное в среде излучение источника и вторичное излучение учитывают введением в закон ослабления в геометрии узкого пучка сомножителя -– фактора накопления фотонного излучения :

(31)

Из этой формулы следует, что 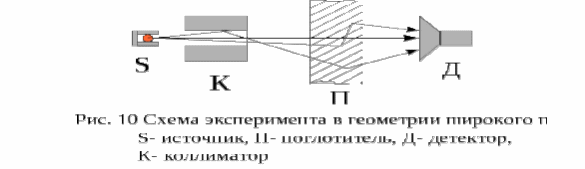представляет собой отношение общего числа фотонов (не рассеянных, рассеянных и вторичных) к числу не рассеянных фотонов, которое определяется как .



Рис. 15. Схема эксперимента в геометрии широкого пучка:

S – источник, К – коллиматор, П – поглотитель, Д – детектор


В общем случае если обозначить через G₀ некоторый функционал, описывающий поле не рассеянного первичного излучения, а через G_S – поле рассеянного и вторичного излучений, то фактор накопления по данному эффекту (числу частиц, дозе, интенсивности и т.д.) равен

В=(G₀+G_S)/G₀=1+G_S/G₀ (32)

Фактор накопления равен кратности превышения характеристик поля не рассеянного, рассеянного и вторичного излучения над характеристиками поля только не рассеянного излучения. Можно сказать, что фактор накопления (ФН) равен отношению показания детектора при измерении в геометрии широкого пучка к показанию детектора при измерении в геометрии узкого пучка.

ФН зависит от многих условий задачи: от того, какая характеристика поля излучения регистрируется, от геометрии, от спектра и углового распределения источника, от толщины и материала защиты, от взаимного расположения источника и детектора.

В зависимости от регистрируемых характеристик поля излучения различают следующие ФН (определения даются для первичного излучения с энергией Е₀).

Числовой ФН (для плотности потока фотонов ):

В_ч(х) =  (Е,x) dE / (Е₀,x)

Энергетический ФН (для интенсивности фотонов):

В_э(х) =  (Е,x)E dE / ((Е₀,x)Е₀)

Дозовый ФН (для поглощённой дозы в воздухе, для экспозиционной дозы):

В_D(х) =  (Е,x) E _а^в(E) dE / ((Е₀,x) Е_{0 а} ^в (Е₀) ),

здесь _а^в(Е) – коэффициент поглощения энергии фотонов в воздухе.

ФН поглощённой энергии (для поглощённой в среде энергии):

В_п(х) =  (Е,x) E _а^ср(E) dE / ((Е₀,x) Е_{0 а}^ср (Е₀) ),

здесь _а^ср(Е) – коэффициент поглощения энергии в данной среде .

Отметим, что дозовый ФН равен ФН поглощённой энергии в воздухе.

Польза от применения ФН заключается в том, что с его помощью можно записать закон ослабления широкого пучка, который как правило имеет место в реальной ситуации, в том же простом виде, что и для узкого пучка (4). Например, для плотности потока частиц :

(x) = ₀ exp(x) В_ч(х) (33)

Аналогично можно записать закон ослабления для интенсивности излучения, дозы, мощности дозы и т.д., используя соответствующее значение ФН. Без использования ФН расчёт поля излучения в практических ситуациях требует точного расчёта рассеянного и вторичного излучения, что выполнить очень сложно.

Удобство применения ФН заключается также в том, что он изменяется достаточно плавно в зависимости от x, Е₀ и Z вещества и можно проводить достаточно точную интерполяцию ФН по ограниченному числу расчётных и экспериментальных данных. Наиболее часто используют следующие аппроксимационные формулы:

Формула Бергера: В(x) = 1+axexp(bx) (x  10)

Коэффициенты а и b приводятся в специальных таблицах.

Формула Тейлора: В(Е₀, x, Z) = А₁exp(-₁x) + (1-А₁) exp(-₂x).

Коэффициенты А₁ , ₁ , ₂ имеются в таблицах в литературе.

Если первичное излучение имеет непрерывный спектр (что часто имеет место в действительности), то вычисление ФН необходимо проводить следующим образом:
В(x)=S(Е) В(Е, x) dE,

где S(E) – спектр источника.

ФН зависит от многих переменных, поэтому самым надёжным методом для его расчётов является метод статистического моделирования – метод Монте-Карло.

Основные закономерности поведения фактора накопления:

• 
  ФН монотонно возрастает с увеличением толщины вещества, так как увеличивается доля фотонов, испытавших рассеяние. Для высоких энергий и материалов с небольшими Z скорость возрастания ФН почти линейная от толщины. Для элементов с большим Z ФН растет медленнее за счет большего фотопоглощения.
  
• 
  ФН возрастает при увеличении изотропии источника, при этом для постоянного расстояния между источником и детектором справедливо следующее соотношение: В_  В _бар  В _огр , т.е. наибольший ФН в бесконечной среде.
  
• 
  ФН при одной энергии фотонов больше в веществах с меньшим Z, где меньше сечение фотоэффекта, который приводит к поглощению излучения при большой энергии фотонов он больше в веществах с большим за счёт интенсивной генерации вторичного излучения;
  
• 
  ФН зависит от поперечных размеров источника и возрастает с их увеличением.
  

В таблице 5 приводятся конкретные значения ФН для двух веществ. Из неё видны основные закономерности ФН, отмеченные выше. Из таблицы также следует, что на больших расстояниях от источника вклад рассеянного излучения в поле излучения является преобладающим и может в десяткисотни раз превышать вклад от не рассеянного излучения.

В качестве примера на рис. 16 и 17 приведены дозовые факторы накопления в бесконечной среде (бетон, железо) при разных энергиях источника.
Таблица 5

Дозовые ФН для точечного изотропного источника в бесконечной среде

E0 , МэВ	x, воздух					x, железо
	1	2	4	10	20	1	2	4	10	20
0,2	3,28	7,74	25,6	192	1220	1,86	2,59	4,08	8,90	17,6
1,0	2,08	3,60	7,60	25,8	72,8	1,85	2,85	5,30	15,8	41,3
6,0	1,52	1,97	2,85	5,42	9,58	1,47	1,87	2,76	6,18	14,2

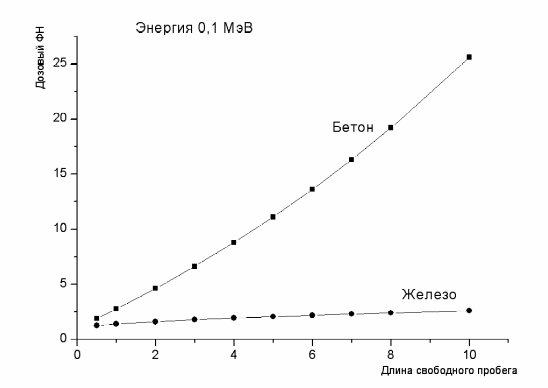Рис. 16. Дозовые факторы накопления изотропного

источника в бесконечной среде.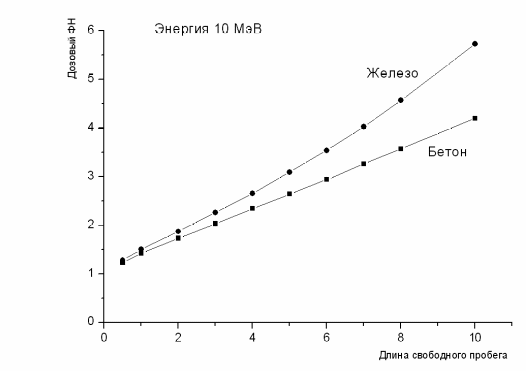


Рис. 17. Дозовые факторы накопления изотропного

источника в бесконечной среде.


Задание №6

• 
  Измерить коэффициенты ослабления -излучения в Al, Fe и Cu.
  
• 
  Определить энергию -излучения радиоактивного источника.
  
• 
  Оценить вклад различных процессов взаимодействия
  

-излучения с веществом в полное сечение.
В качестве источника -квантов используется -активный изотоп ₂₇Со⁶⁰ с периодом полураспада 5,27 года. Схема распада ₂₇Со⁶⁰ приведена на рис.18. Из-за большой разницы в спинах (5+  0+ и 5+  2+) практически не происходит -распад ядра кобальта в основное и первые возбуждённые состояния никеля, а идёт на высший возбуждённый уровень (5+  4+). Переход ядра никеля из возбуждённого состояния в основное является сильно запрещённым вследствие большой мультипольности -кванта (Е4), поэтому испускаются два каскадных -кванта. Оба -кванта излучаются при электрических квадрупольных переходах (Е2), т.е. практически испускаются только фотоны с энергиями 1,333 МэВ и 1,172 МэВ, средняя энергия излучения 1,25 МэВ. Так как -кванты, испускаемые ядром Ni, вызваны -распадом ядер Со, то и -активность источника спадает с периодом 5,27 года. Энергия -частиц мала (Е_гр=0,32 МэВ) и они полностью поглощаются в стенках ампулы, в которую заключён источник. Для -излучения эти стенки практически прозрачны.

Рис. 18. Схема распада ₂₇Со⁶⁰

Для вычисления коэффициентов ослабления необходимо получить зависимости (4) ослабления потока -квантов от толщины поглотителя в условиях узкой геометрии. После логарифмирования этой зависимости получаем в полулогарифмическом масштабе линейную зависимость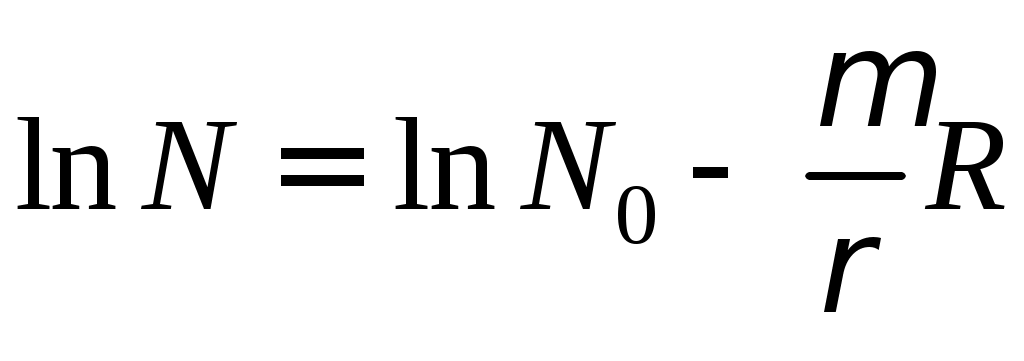

, (34)

угол наклона которой и даёт искомую величину.

Экспериментальное создание узкой геометрии (рис. 2) связано с необходимостью хорошей коллимации пучка, что требует использования источника большой активности. Кроме того, возникают проблемы, связанные с рассеянием фотонов в стенках каналов коллиматоров. Указанных трудностей можно избежать, если для регистрации -квантов использовать спектрометрический детектор, позволяющий выделять события, связанные с регистрацией фотонов с начальной энергией, т.е. не испытавших взаимодействия с веществом поглотителя. В данной работе для регистрации -излучения используется сцинтилляционный спектрометрический детектор с размерами кристалла NaI(Tl): диаметр – 185 мм, высота – 155 мм. Схема эксперимента показана на рис. 19.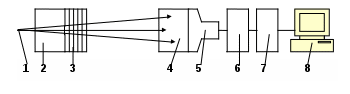



Рис. 19. Упрощённая схема эксперимента:

1 – источник, 2 – коллиматор, 3 – поглотитель, 4 – сцинтиллятор,

5 – ФЭУ, 6 – усилитель, 7 – АЦП, 8 – компьютер
Детектор используется в составе программно-аппаратного комплекса «Анализатор амплитудного спектра», программное обеспечение которого позволяет проводить статистическую обработку отдельных участков спектра, выделенных маркерами. Выделяя маркерами область пика полного поглощения, мы находим количество полностью поглотившихся в кристалле фотонов с энергией, равной начальной Е₀.

Но не каждый попавший в кристалл фотон с энергией Е₀ поглощается полностью и создаёт импульс, амплитуда которого попадает в пик полного поглощения. Доля полностью поглотившихся квантов определяется величиной фотовклада Р. Если в кристалл попало N квантов с энергией Е₀, то в пике полного поглощения будет зарегистрировано N_р=NP событий. С учётом этого уравнение (4) приобретает вид:

. (35)
Но , где – число зарегистрированных импульсов при . Поэтому окончательно:
(36)

(37)
Порядок выполнения работы

1. 
   Ознакомится с описанием программно-аппаратного комплекса ”Анализатор амплитудного спектра”.
   
2. 
   Включить установку в сеть.
   
3. 
   Включить питание крейта КАМАКа тумблером на нижней правой панели крейта. Загорится зелёная сигнальная лампочка.
   
4. 
   Включить ЭВМ и в окне ОS DOS запустить программу по адресу ANALIZ  /mine.exe/. После загрузки компьютера загорится красная лампочка на контроллере КАМАКА «крейт выбран».
   
5. 
   Установить на место -источник. Геометрию измерений выбрать таким образом, чтобы не рассеянные кванты не попадали на края сцинтиллятора.
   
6. 
   Выбрать пункт меню «Накопление спектра». Установить ширину окна в 300 каналов ( левый канал – 0, правый канал – 300). Командой «Часть» установить выбранные границы отображения спектра.
   
7. 
   Запустить накопление и подобрать напряжение на ФЭУ и коэффициент усиления таким образом, чтобы спектр амплитуд импульсов после усиления укладывался в шкалу анализатора (в интервал между маркерами).
   
8. 
   Остановить накапливание и маркерами выделить пики полного поглощения. Построение кривой ослабления производить по данным, полученным с выделенного участка (поле «Расчет»).
   
9. 
   Удалить -источник и измерить скорость счета импульсов фона. Время измерения подбирать таким образом, чтобы статистическая ошибка не превышала %.
   
10. 
    Установить -источник и снять кривые ослабления для веществ с разными значениями . Время измерения выбрать таким образом, чтобы статистическая ошибка измерения не превышала 3%. Данные занести в таблицы:
    

Материал поглотителя – Z = ,  = , nф= .
x, см		Число отсчетов N	Время из­- мерения	Скорость счета
0 x1

11. 
    В терминале OS Linux запустить программу "exp1". Ввести через пробел значения и (начиная с =0). Ввести значение . Программа находит уравнения прямых, аппроксимирующих экспериментально полученные зависимости для различных материалов, выдаёт значение и статистическую ошибку.
    
12. 
    Найденные аппроксимирующие прямые для разных поглотителей построить на одном графике. На этом же графике проставить экспериментальные точки .
    
13. 
    По найденным значениям вычислить линейные коэффициенты ослабления (макроскопические се­чения) и микроскопические сечения и . Результаты занести в таблицу:
    

Вещество	Z

14. 
    Указать погрешность измеренных значений коэффициентов ослабления.
    
15. 
    Используя графики на рис.13 или 20 оценить энергию -квантов источника. Поскольку спектр излучения содержит две близкие по энергии линии и разделить их по кривой ослабления невозможно, определяется усредненное значение энергий квантов, точнее такое значение энергии монохроматического пучка, для которого коэффициент ослабле­ния равен найденному.
    
16. 
    Оценить степень согласия результатов опыта с экспоненциальным законом по -критерию.
    17. Используя программу компьютерного моделирования прохождения излучения через вещество PCLab промоделировать траектории фотонов в легких и тяжелых материалах при разных энергиях и качественно объяснить результат. По той же программе просчитать кривую ослабления для одного из материалов. Построить кривую ослабления и вычислить коэффициент ослабления, сравнить с экспериментом.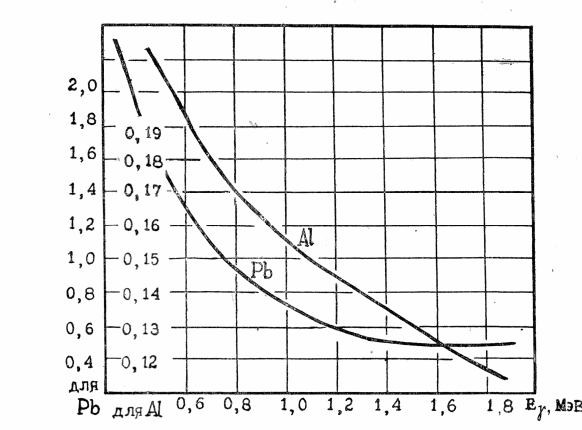