Сопло Лаваля представляет собой канал с переменной по длине проточной части площадью проходного сечения
 Скачать 438.5 Kb. Скачать 438.5 Kb.
|
|
Введение Сопло Лаваля представляет собой канал с переменной по длине проточной части площадью проходного сечения. Сопла Лаваля находят широкое применение в тепловых двигателях и энергоустановках (сопловых аппаратах паровых и газовых турбин, камерах ракетных двигателей и т.д.). Расчет течения потока в сопле Лаваля заключается в определении его параметров (скорости, давления, температуры, напряжения трения) в интересующих точках проточной части. В настоящее время предпочтительным считается выполнение расчета в два этапа с выделением в движущемся потоке двух областей – потенциального ядра и пограничного слоя. Такой подход позволяет существенно упростить расчет, поскольку оказывается возможным в ядре потока пренебречь влиянием сил вязкости и считать течение идеальным, а в пограничном слое из-за малой его толщины – пренебречь членами уравнения движения и энергии, содержащими вторые производные скорости и температуры по продольной координате. Поскольку заранее граница между указанными областями течения не известна, то расчет проводят методом последовательных приближений: сначала, пренебрегая толщиной пограничного слоя, рассчитывают идеальное течение в пределах всей проточной части сопла, а затем, используя в качестве граничных условий найденное распределение параметров по его длине, рассчитывают пограничный слой. По результатам расчета пограничного слоя определяются в частности его условные толщины (вытеснения, потери импульса, потери энергии) и напряжение трения потока на поверхности стенки. Во втором приближении область идеального течения в каждом сечении сопла уменьшается на толщину вытеснения пограничного слоя в этом сечении, расчет ядра потока повторяется, а параметры течения уточняются. Затем повторяется и расчет пограничного слоя. Как правило, уже после 2-го приближения достигается удовлетворительная точность расчетов. 1. РАСЧЕТ ИДЕАЛЬНОГО ТЕЧЕНИЯ В ЯДРЕ ПОТОКА При сверхкритическом перепаде давления поток рабочего тела при движении по тракту сопла Лаваля (рис. 1.1) интенсивно ускоряется, достигая на выходе сверхзвуковых скоростей. Минимальное сечение сопла называют критическим. Параметры потока в критическом сечении называют критическими.  Рис. 1.1. Сопло Лаваля В общем случае параметры потока в осесимметричном сопле Лаваля изменяются как в осевом (вдоль координаты На входе в сопло поток движется с дозвуковой скоростью. В критическом сечении скорость потока достигает скорости звука Отношение площадей, занятых невязким ядром в критическом и анализируемом сечениях, представляет собой газодинамическую функцию где При расчете функции Максимальное свое значение, равное 1, функция Связь между функцией где Получить точное аналитическое решение уравнения (1.3) для определения коэффициента скорости Рассмотрим суть метода последовательных приближений. Пусть дано уравнение вида Требуется отыскать вещественные (действительные) корни этого уравнения. Заменим исходное уравнение (1.4) эквивалентным ему уравнением Следует заметить, что переход от уравнения (1.4) к уравнению (1.5) может быть выполнен в общем случае разными вариантами. Например, переход от уравнения (1.3) к уравнению вида (1.5) может быть выполнен следующими вариантами 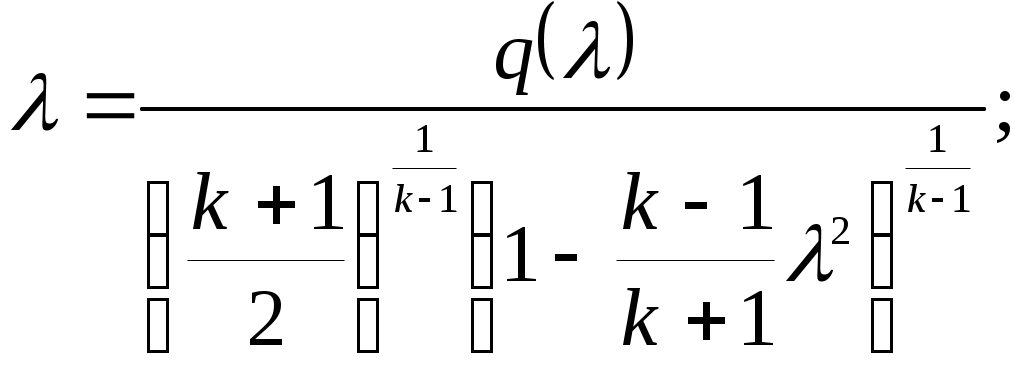 (1.6) (1.6)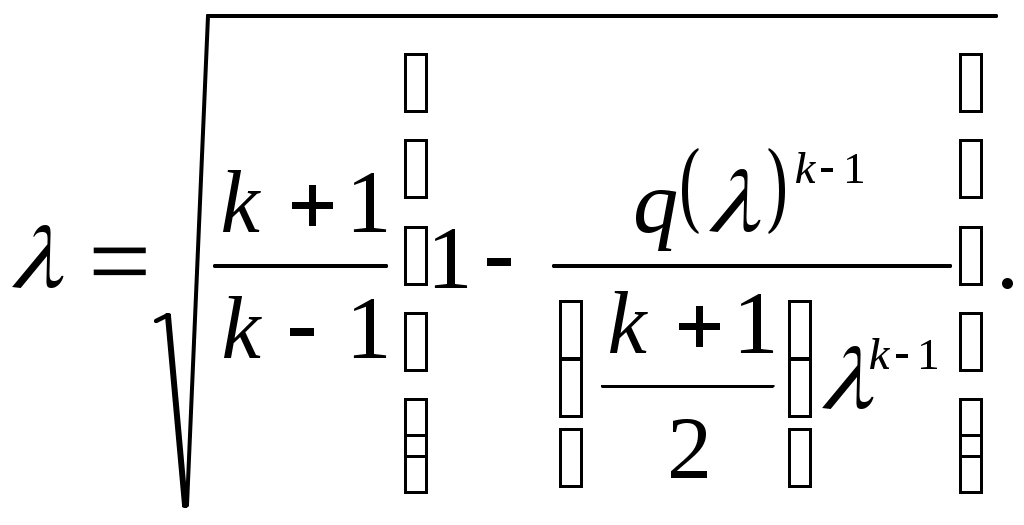 (1.7) (1.7)Далее в уравнении вида (1.5) выбирается начальное приближение где i – номер итерации. Если итерационный процесс (1.8) сходится, т.е. значение Практически сходящийся итерационный процесс прерывается при некотором значении Не вдаваясь в детали анализа условий сходимости решения, отметим, что реализация схемы (1.6) для уравнения (1.3) обеспечивает сходимость решения в сужающейся части сопла Лаваля, где поток движется с дозвуковой скоростью, а коэффициент скорости Решение удобно выполнить с помощью компьютера. Алгоритм решения задачи можно представить следующим образом 1. Задаем значения исходных величин Замечание: при анализе параметров течения в сечении, расположенном в сужающейся части сопла Лаваля, начальное приближение 2. Уточняем значение 3. Определяем погрешность решения 4. Если окажется, что С программой, реализующей рассмотренный алгоритм, можно ознакомиться в работе [4]. Более простой, но значительно менее точный способ отыскания коэффициента скорости По найденному в каждом сечении сопла значению коэффициента скорости Критическая скорость звука где Массовый расход где Входящий в соотношение (1.12) коэффициент Абсолютные значения скорости в ядре потока, его давления, температуры, плотности в каждом сечении сопла могут быть найдены по формулам Найденные значения параметров могут быть использованы при расчете пограничного слоя в качестве граничных условий на его внешней границе. 2. Расчет пограничного слоя в соплах В результате расчета пограничного слоя определяется сопротивление трения потока на поверхности сопла, толщина вытеснения, необходимая для корректного расчета параметров в ядре потока, а также многие другие локальные и интегральные характеристики. Расчет пограничного слоя в соплах является достаточно сложной задачей. Движение потока в пограничном слое сопел в большинстве случаев является турбулентным. Оно осложняется большими скоростями движения, сжимаемостью потока, существенным влиянием продольного отрицательного градиента давления на осредненные параметры турбулентного течения и на интенсивность турбулентного переноса. Достаточно полный и строгий учет влияния этих особенностей возможен лишь при использовании дифференциальных методов расчета пограничного слоя, основанных на применении численных методов интегрирования системы его дифференциальных уравнений и компьютерной техники. 2.1. Система уравнений пограничного слоя и граничные условия Система уравнений стационарного пограничного слоя для рассматриваемых условий может быть представлена в виде (см., например, [5,6]): уравнение движения уравнение энергии уравнение неразрывности уравнение состояния Здесь x, y – координаты, направленные вдоль поверхности, обтекаемой потоком (вдоль криволинейной образующей сопла), и по нормали к ней; r – расстояние от рассматриваемой точки до оси сопла; ρ, μ, λ, Если в уравнениях (2.1), (2.2) принять Величины u, v, ρ, T, p, входящие в уравнения (2.1) – (2.4), для турбулентного режима течения полагаются осредненными за период времени Граничные условия однозначности для задачи расчета пограничного слоя можно представить в виде Условие Система (2.1) – (6.4), включающая четыре уравнения, содержит при ламинарном режиме течения четыре неизвестных величины u, v, T, ρ и является замкнутой. При турбулентном режиме течения система уравнений включает шесть неизвестных величины u, v, T, ρ, Используя гипотезу Прандтля о пути смешения l, получим Длина пути смешения в пограничном слое может быть рассчитана по выражению, предложенному Прандтлем, с поправкой Ван-Дрийста1 Здесь безразмерная координата определяется соотношением где Для определения коэффициента турбулентного переноса æ в стационарном пограничном слое в соплах можно воспользоваться формулой, предложенной автором [6]  (2.11) (2.11)Здесь индекс Связь между коэффициентами турбулентного переноса где При расчетах стационарного пограничного слоя можно принять 2.2. Численный метод решения Анализ различных разностных схем для решения системы уравнений пограничного слоя показывает, что наиболее удобными являются неявные шеститочечные схемы. Для составления такой схемы на координатной плоскости x, y выбираются основная и две вспомогательные сетки. Координаты узлов основной сетки Координаты узлов вспомогательных сеток Здесь i, j – целые числа (0, 1, 2, ...); Значения любого из параметров u, v, T, μ и т.п. в узлах основной или вспомогательных сеток обозначают следующим образом: Используя метод разностной аппроксимации производных применительно к уравнениям (2.1) – (2.3), получают их разностную схему. Так, например, разностный аналог (разностная схема) уравнения (2.1) имеет вид 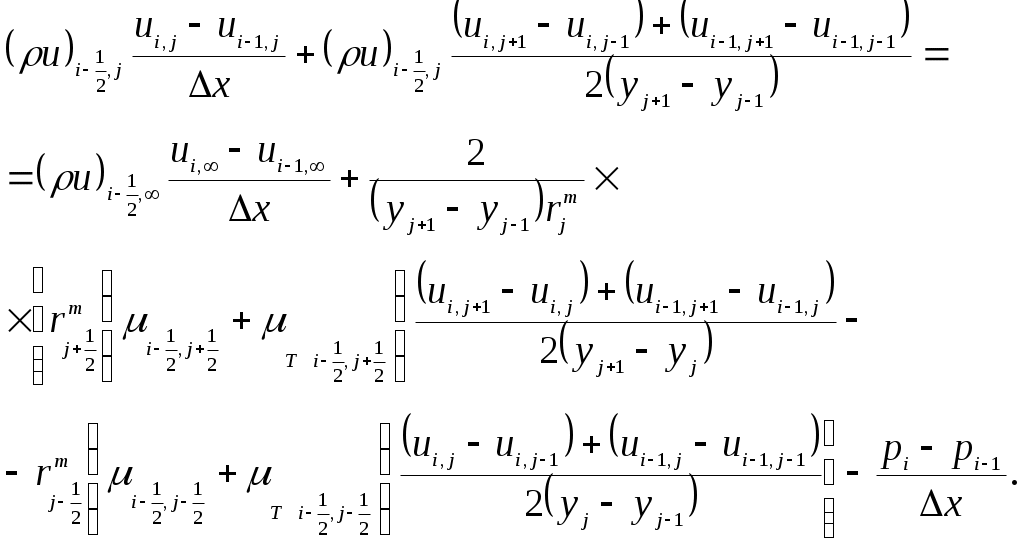 (2.15) (2.15)Разностное уравнение энергии (2.15) представляется в более компактной форме где коэффициенты Аналогично получают разностный аналог дифференциального уравнения энергии (2.2). Алгебраическое уравнение (2.16) совместно с разностным уравнением неразрывности решается методом прогонки. При этом решение уравнения (2.16) представляется в форме Прогоночные коэффициенты Расчет структуры пограничного слоя осуществляется последовательно, начиная с сечения i= 1, при этом все параметры потока в предыдущем сечении i= 0 известны из граничных условий для х = 0. В каждом расчетном сечении сначала определяются прогоночные коэффициенты По результатам расчета структуры пограничного слоя в интересующих сечениях потока определяются коэффициент трения толщина вытеснения безразмерные скорости φ и координаты η По полученным данным о структуре могут быть найдены и другие локальные и интегральные характеристики пограничного слоя. Более подробно численный метод интегрирования дифференциальных уравнений пограничного слоя изложен в работе [6]. 2.3. Программа расчета Рассмотренный численный метод расчета пограничного слоя реализован в виде программы “POGR” на алгоритмическом языке Microsoft QuickBASIC. Текст программы с содержащимся в ней базовым комплектом (базой) исходных данных приведен в приложении 3. Эта программа может быть переписана преподавателем на дискету студента. Программа оперирует с относительными безразмерными параметрами, поэтому большая часть исходных данных и результатов расчета представляются в безразмерном виде. Приведение параметров к безразмерному виду осуществляется с помощью выражений (безразмерные параметры снабжены верхней чертой) Здесь нижний индекс Базовый комплект исходных данных позволяет рассчитать турбулентный пограничный слой на гладкой непроницаемой поверхности одного из сопел конкретной геометрии при течении воздушного потока с учетом зависимости его теплофизических свойств от температуры. Работа с программой сводится к подготовке и вводу изменений в базовый комплект исходных данных и выполнения соответствующих расчетов. Внося изменения в базовый комплект данных, можно смоделировать различные условия течения. Значения параметров, которые должны быть изменены, располагаются в тексте программы между двумя строками с комментариями в виде пунктирной линии: rem ----------------------------------------------------------------- rem Количество расчетных сечений M3%=59 rem Масштабное значение скорости (м/с) - скорость на входе в сопло uz=36. rem Давление (Па) и температура (К) заторможенного потока pz=70e05:Tz=1473 rem Масштабное значение динамического коэффициента вязкости потока (Па*с) mz=0.535e-04 rem Масштабное значение удельной изобарной теплоемкости потока (Дж/(кг*К)) cpz=1210 roz=pz/(Rz*Tz):kz=roz*uz/(1000*mz) rem Координаты расчетных сечений вдоль образующей сопла (мм) data 0.,5.,10.,15.,20.,25.,30.,35.,40.,45.,50.,55.,60.,65.,70.,75.,80 data 85.02,90.05,95.15,100.5,106.1,112.2,117.8,123.9,129.3,135.4,141.2 data 146.8,152.2,157.3,162.5,167.8,172.9,178.1,183.2,188.4,193.5,198.6 data 203.8,209,214.1,219.3,224.4,229.6,234.8,239.9,245.1,250.2,255.4 data 260.5,265.7,270.8,276.0,281.1,286.3,291.4,296.6,301.7 for J%=1 to M3%: read XB(J%):XB(J%)=kz*XB(J%):next J% rem Диаметры проточной части в расчетных сечениях (мм) data 100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100 data 99,98,96,92,87,80,75,68,64,57,51,46,42,40,43,46,48.5,51,53.5,56,58.5 data 61,63.5,66,68.5,71,73.5,76,78.5,81,83.5,86,88.5 data 91,93.5,96,98.5,101.0,103.5,106,108.5,110 for J%=1 to M3%: read DB(J%):DB(J%)=kz*DB(J%):next J% rem Относительная скорость в ядре потока в расчетных сечениях data 1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1. data 1.02,1.042,1.086,1.184,1.326,1.573,1.795,2.199,2.498,3.205,4.125,5.34 data 7.082,9.816,13.2,14.46,15.22,15.83,16.33,16.76,17.14,17.47,17.76,18.03 data 18.27,18.49,18.69,18.87,19.04,19.2,19.35,19.48,19.61 data 19.73,19.85,19.95,20.05,20.15,20.24,20.32,20.40,20.45 for J%=1 to M3%: read UB(J%): next J% rem -----------------------------------------------------------------. При подготовке исходных данных необходимо изменить численные значения указанных в этой части программы параметров на те, которые соответствуют индивидуальному заданию на курсовую работу. Единицы измерения параметров также указаны в комментариях к программе. Замечания: 1. Количество введенных в базу данных значений координат расчетных сечений (вдоль образующей сопла), диаметров проточной части и относительных скоростей в ядре потока в этих сечениях должно быть одинаковым и численно равным введенному количеству расчетных сечений. 2. Масштабные значения динамического коэффициента вязкости и удельной изобарной теплоемкости потока выбираются из таблицы приложения 2 по температуре заторможенного потока T*. В программе предусмотрено отображение результатов расчета в графической и табличной формах. При графическом отображении на экран дисплея (а при желании исследователя и на бумажный носитель) выдаются графики зависимостей а также профили скорости в сечениях пограничного слоя, построенные в координатах Здесь Результаты численного расчета при их графическом отображении представляются на графиках в форме дискретных условных знаков (точек). На этих же графиках в виде линий изображаются результаты, соответствующие ламинарному и турбулентному течению в “стандартных” (эталонных) условиях. Под “стандартными” условиями понимают обтекание гладкой непроницаемой пластины стационарным безградиентным потоком несжимаемой жидкости с постоянными (не зависящими от параметров состояния) свойствами. Для “стандартных” условий при ламинарном режиме течения потока справедливы следующие зависимости для коэффициента трения Для турбулентного потока зависимости для коэффициента трения Профили скорости в турбулентном пограничном слое для “стандартных” условий аппроксимируются зависимостями для вязкого подслоя (η > 11,5) для турбулентного ядра Отображению результатов численного расчета в табличной форме предшествует выдача таблиц исходных данных для выполненного варианта расчета. Отображение результатов численного расчета в табличной форме осуществляется последовательно для всех сечений, выбранных в качестве расчетных. Для каждого сечения выводятся три массива информации, отделенные друг от друга интервалом. В первом массиве содержится семь строк. В первой строке выводится значение текущего значения числа Второй массив информации содержит семь столбцов. В первом столбце приведены номера расчетных точек j поперек полосы интегрирования; во втором столбце – соответствующие значения величин Третий массив информации содержит шесть столбцов. В первом столбце также приведены номера расчетных точек j; во втором столбце – соответствующие значения величин Пример отображения результатов расчета в графической форме представлен в приложении 4, а в табличной форме – в приложении 5. 3. Задание на курсовую работу В сопле Лаваля заданной формы и размеров (см. рис. 3.1) движется воздушный поток. Размеры сопла выражаются соотношениями: 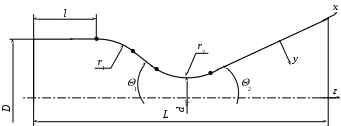 Рис. 3.1. Геометрия сопла Лаваля Требуется рассчитать и построить графики изменения по длине сопла скорости 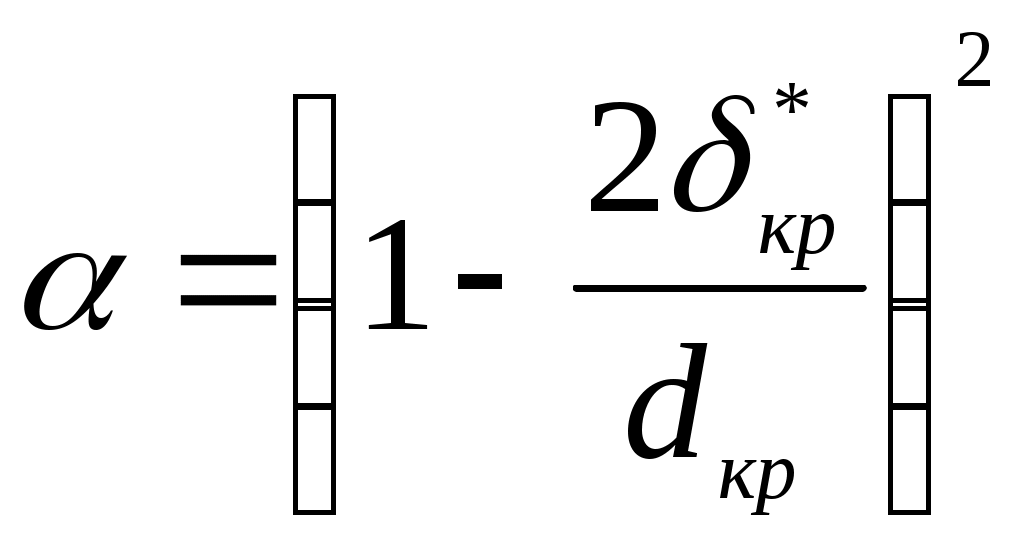 , где , где Замечание. Используемая в расчетах система координат (x, y, z) показана на рис. 3.1. 4. Порядок выполнения работы 4.1. На миллиметровке формата А4 в удобном (максимально крупном) масштабе строится профиль сопла, выделяется его критическое (минимальное) сечение и измеряется его диаметр 4.2. Определяются криволинейные (вдоль образующей сопла) координаты 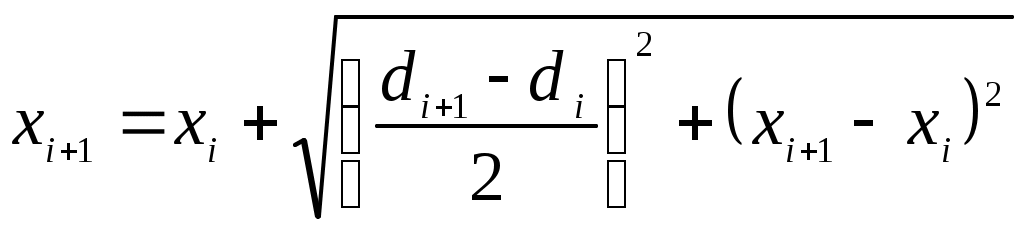 . (4.1) . (4.1)4.3. По выражению (1.2) рассчитывается значение газодинамической функции 4.4. По формулам (1.10) последовательно во всех расчетных сечениях определяются газодинамические функции 4.5. По формуле (1.11) рассчитывается критическая скорость звука 4.6. По формулам (1.12), (1.13) рассчитывается расход рабочего тела в каждом выделенном сечении и контролируется правильность расчетов путем проверки постоянства (в пределах точности вычислений) расхода во всех сечениях 4.7. По выражениям (1.14) определяются абсолютные значения скорости в ядре потока u, его давления p, температуры T, плотности 4.8. Определяются относительные значения скорости 4.9. Вносятся изменения в базу данных программы “POGR” в соответствии с инструкцией, изложенной в подразделе 2.3. 4.10. Выполняется расчет пограничного слоя на компьютере. 4.11. По результатам расчета пограничного слоя во всех выделенных сечениях определяются коэффициент трения 4.12. Во всех выделенных сечениях рассчитывается напряжение трения 4.13. Рассчитывается коэффициент расхода сопла 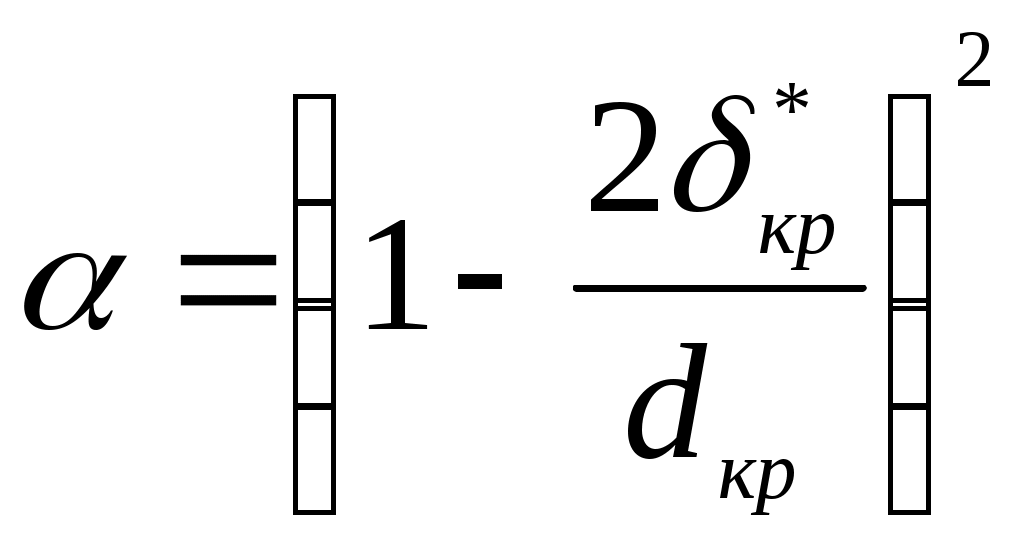 . .4.14. Производится уточнение результатов путем повторения пп. 4.3 – 4.13 до достижения требуемой точности (пока разность значений каждого из параметров u, p, T, 4.15. Результаты расчета, полученные в первом и последнем приближениях, отображаются в виде графиков. 1 Поправка Ван-Дрийста представляет собой сомножитель в правой части выражения (2.9), заключенный в квадратные скобки. Этот сомножитель учитывает интенсивное гашение турбулентных пульсаций вблизи стенки в вязком подслое. |
