информатика 9 класс. Сортировка массива

• Название: Сортировка массива
• Дата: 12.04.2022
• Размер: 122.19 Kb.
• Имя файла: информатика 9 класс.docx
• Тип: Практическая работа; #466915

9 класс

Сортировка массива.

Под сортировкой (упорядочением) массива понимают перераспределение значений его элементов в некотором определённом порядке.

Порядок, при котором в массиве первый элемент имеет самое маленькое значение, а значение каждого следующего элемента не меньше значения предыдущего элемента, называют возрастающим.


Порядок, при котором в массиве первый элемент имеет самое большое значение, а значение каждого следующего элемента не больше значения предыдущего элемента, называют убывающим.

Цель сортировки — облегчить последующий поиск элементов: искать нужный элемент в упорядоченном массиве легче. Вы уже встречались с сортировкой при работе с базами данных. Сейчас мы рассмотрим один из возможных вариантов реализации механизма этой операции — сортировку выбором.


Сортировка выбором (например, по убыванию) осуществляется следующим образом:

1. 
   В массиве выбирается максимальный элемент;
   
2. 
   Максимальный и первый элементы меняются местами (первый элемент считается отсортированным);
   
3. 
   В неотсортированной части массива снова выбирается максимальный элемент; он меняется местами спервым неотсортированным элементом массива;
   
4. 
   Действия, описанные в пункте 3, повторяются с неотсортированными элементами массива до тех пор, пока неостанется один неотсортированный элемент (его значение будет минимальным).
   

Рассмотрим процесс сортировки выбором на примере массива a={0,1,9,2,4,3,6,5}.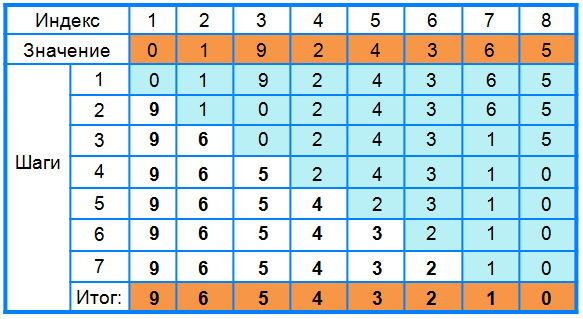



В этом массиве из восьми элементов операцию выбора максимального элемента мы проводили 7 раз. Вмассиве из n элементов такая операция будет проводиться n−1 раз.


Практическая работа № 4

program  n_8;

var n, i, j, x, imax: integer;

a:array[1..10] of integer;

begin 

for i:=1 to 10 do read (a[i]);

for i:=1 to 10 do write (a[i],` `);

for i:=1 to 9 do

begin

imax:=i;

for j:=i+1 to 10 do if a[j]>a[imax] then imax:=j;

x:=a[i];

a[i]:=a[imax];

a[imax]:=x

end;

for i:=1 to 10 do write (a[i],` `);

end.

9 класс

Конструирование алгоритмов

Цель урока: рассмотреть примеры и получить опыт решения типовых задач по обработке массивов (суммирование, поиск, наименьшего / наибольшего значения, подсчет количества элементов с некоторым свойством); познакомиться с сущностью процесса сортировки массива, сформировать умение записывать на языке программирования короткие алгоритмы обработки одномерных массивов.

Ход урока.

1. 
   Организационный момент.
   
2. 
   Проверка домашнего задания.
   
3. 
   Основная часть урока.
   

Новый материал излагается в сопровождении презентации

Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся содним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называетсяметодом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.

Процесс последовательного построения алгоритма выглядит следующим образом.

На первом шаге мы считаем, что перед нами совершенный исполнитель, который всё знает и всё умеет.Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в видеединого предписания — постановки задачи.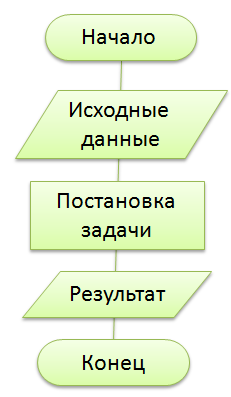



Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание ввиде совокупности более простых предписаний (команд). Для этого:

• 
  задачу разбивают на несколько частей, каждая из которых проще всей задачи;
  
• 
  решение каждой части задачи формулируют в отдельной команде, которая также может выходить за рамки системы команд исполнителя;
  
• 
  при наличии в алгоритме предписаний, выходящих за пределы возможностей исполнителя, такие предписания вновь представляются в виде совокупности ещё более простых предписаний.
  

Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.

Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закреплена.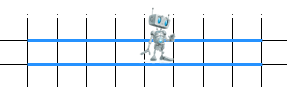




 

Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходноеположение.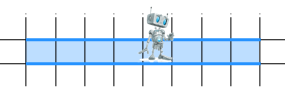

 



 

Представим план действий Робота следующими укрупнёнными шагами (модулями):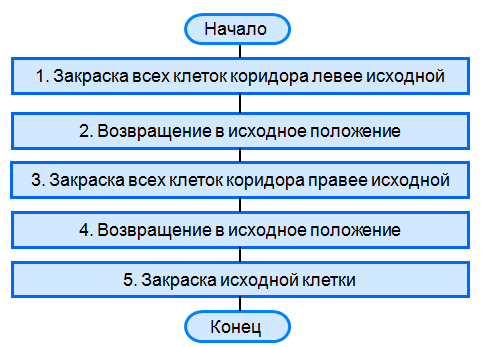

  



 

Детализируем каждый из пяти модулей.

 

1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл ПОКА:

  



 

Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.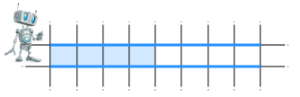

  



 

2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.

 



 

Под управлением этого алгоритма Робот окажется в исходной точке.

  



 

3. Выполнив команду вправо, Робот пройдёт исходную клетку и займёт клетку правее исходной. Теперь можно закрашивать клетки коридора, расположенные правее исходной.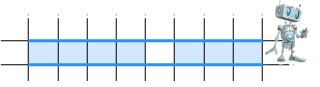

 



 



 

4. Так как, выполнив предыдущий алгоритм Робот оказался правее коридора, командой «влево» вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:

 



 



 

5. По команде «закрасить» Робот закрашивает исходную точку.

При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполнение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.

Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.

При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс», внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.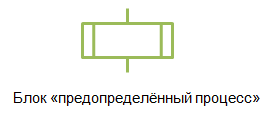




 

Вспомогательный алгоритм делает структуру алгоритма более понятной.

 

Построим алгоритм вычисления степени y=ax, где x — целое число, a≠0.

По определению степени с целым показателем.

 

a0=1,a≠0;a−n=1an,a≠0,n∈N.

 

Исходя из определения и учитывая, что 1a−x=(1a)−x, можно записать: y=⎧⎩⎨⎪⎪⎪⎪1  при x=0ax при x>0(1a)−x при x<0.

 

Решение задачи вычисления степени y=ax, где x — целое число, a≠0, представим блок-схемой: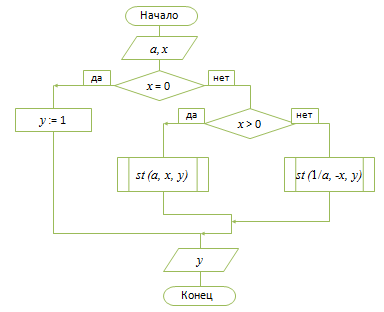

 



 

Этот алгоритм является основным по отношению к вызываемому в нём вспомогательному алгоритму.

 

Напомним, что параметрами используемого вспомогательного алгоритма были величины a,n,y. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т.е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.

 

Команда вызова вспомогательного алгоритма исполняется следующим образом:

1. 
   Формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
   
2. 
   Для заданных входных данных исполняются команды вспомогательного алгоритма:
   
3. 
   Полученные результаты присваиваются переменным с именами фактических результатов;
   
4. 
   Осуществляется переход к следующей команде основного алгоритма.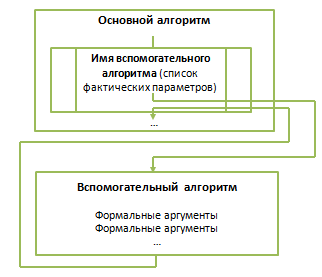
   

 

4. 
     Закрепление.
   
5. 
   Выводы по теме.
   
6. 
   Подведение итогов.
   
7. 
   Домашнее задание: выучить §2.3 ст. 76 -87.