Вариант 1
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: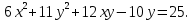 
Составить каноническое уравнение гиперболы, если ее асимптоты имеют уравнения 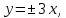 а межфокусное расстояние равно 20.
|
Вариант 2
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,5, а межфокусное расстояние равно 4.
|
Вариант 3
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: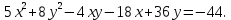 
Составить каноническое уравнение гиперболы, если ее межфокусное расстояние равно 10, а эксцентриситет равен 4.
|
Вариант 4
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: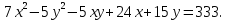 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 4, а малая полуось равна 3.
|
Вариант 5
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: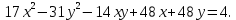 
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,8, а межфокусное расстояние равно 8.
|
Вариант 6
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: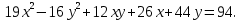 
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 6.
|
Вариант 7
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: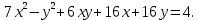
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,8, а межфокусное расстояние равно 6.
|
Вариант 8
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: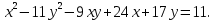 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 4, а большая полуось равна 3.
|
Вариант 9
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: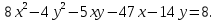 
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 10.
|
Вариант 10
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: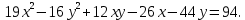 
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,6, а межфокусное расстояние равно 10.
|
Вариант 11
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 5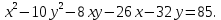
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,1, а межфокусное расстояние равно 2.
|
Вариант 12
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: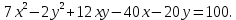 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 6, а малая полуось равна 3.
|
Вариант 13
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: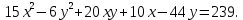 
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 12.
|
Вариант 14
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: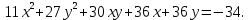 
Составить каноническое уравнение гиперболы, если ее асимптоты имеют уравнения 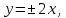 а межфокусное расстояние равно 10.
|
Вариант 15
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: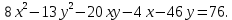 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 4, а большая полуось равна 10.
|
Вариант 16
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: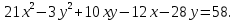 
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,4, а межфокусное расстояние равно 4.
|
Вариант 17
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 7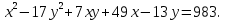
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,2, а межфокусное расстояние равно 14.
|
Вариант 18
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: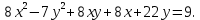 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 8, а малая полуось равна 3.
|
Вариант 19
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 18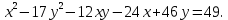
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 20.
|
Вариант 20
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: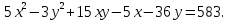 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 4, а большая полуось равна 12.
|
Вариант 21
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: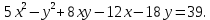 
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,3, а межфокусное расстояние равно 10.
|
Вариант 22
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: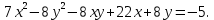 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 10, а малая полуось равна 2.
|
Вариант 23
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 5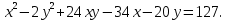
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 4.
|
Вариант 24
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 3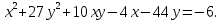
Составить каноническое уравнение гиперболы, если ее асимптоты имеют уравнения 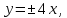 а межфокусное расстояние равно 30.
|
Вариант 25
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 3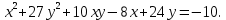
Составить каноническое уравнение гиперболы, если ее межфокусное расстояние равно 40, а эксцентриситет равен 2.
|
Вариант 26
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика:  .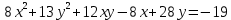
Составить каноническое уравнение гиперболы, если ее асимптоты имеют уравнения 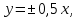 а межфокусное расстояние равно 10.
|
Вариант 27
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 7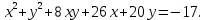
Составить каноническое уравнение эллипса, если его эксентриситет равен 0,9, а межфокусное расстояние равно 10.
|
Вариант 28
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: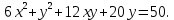 
Составить каноническое уравнение эллипса, если его межфокусное расстояние равно 12, а малая полуось равна 5.
|
Вариант 29
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 3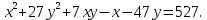
Составить каноническое уравнение гиперболы, если ее асимптоты имеют уравнения 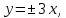а межфокусное расстояние равно 30.
|
Вариант 30
Привести уравнение кривой второго порядка к каноническому виду, найти координаты фокусов и центра (если он есть) в исходной системе координат и построить эскиз графика: 2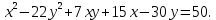
Составить каноническое уравнение параболы, если ее расстояние от фокуса до директрисы равно 14.
|
Скачать 20.48 Kb.