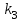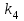Задачи_Лоя. Совместные случайные события могут произойти или не произойти в некотором стохастическом опыте. Составить таблицу наступлений и ненаступлений события в зависимости от наступления и ненаступления событий
 Скачать 353.96 Kb. Скачать 353.96 Kb.
|
|
Задача №1. Совместные случайные события 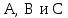 могут произойти или не произойти в некотором стохастическом опыте. Составить таблицу наступлений и ненаступлений события могут произойти или не произойти в некотором стохастическом опыте. Составить таблицу наступлений и ненаступлений события 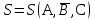 в зависимости от наступления и ненаступления событий в зависимости от наступления и ненаступления событий 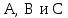 . Построить диаграмму Эйлера и заштриховать . Построить диаграмму Эйлера и заштриховать 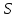 . .
Задача №2. Наудачу выбрано двузначное число. Найти вероятность того, что: сумма цифр выбранного числа не превосходит 8; произведение цифр не превосходит 8; произведение цифр делится на 8. Наудачу выбрано двузначное число  . Найти вероятности событий: . Найти вероятности событий: 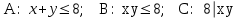 . .Решение. По классическому определению: 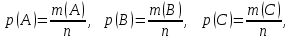 где 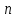 - число элементарных исходов опыта (выбор наудачу двузначного числа), - число элементарных исходов опыта (выбор наудачу двузначного числа), 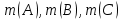 - соответственно: число благоприятных для - соответственно: число благоприятных для 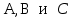 исходов опыта. исходов опыта. Очевидно  . .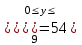 . .Следовательно, 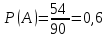 . .  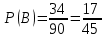 . .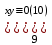 ; заметим, что для каждого ; заметим, что для каждого  сравнение сравнение  имеет два решения, т.к. имеет два решения, т.к.  . Наконец, для . Наконец, для  это сравнение имеет 5 решений это сравнение имеет 5 решений 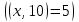 . Таким образом, . Таким образом, . .Ответ: 
Задача №3. В студенческой стройбригаде 10 человек, из которых 4 первокурсника. Из бригады наудачу взяли 3 человек для работы на первом объекте. Найти вероятность того, что среди взятых студентов 1 первокурсников. Решение. Пусть 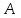 – событие – среди взятых 3-х человек один первокурсник (остальные 1 – не первокурсники). По классическому определению – событие – среди взятых 3-х человек один первокурсник (остальные 1 – не первокурсники). По классическому определению 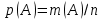 , где , где 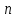 - число всех элементарных исходов опыта (из 10 человек наудачу взяли 4 человека). Тогда - число всех элементарных исходов опыта (из 10 человек наудачу взяли 4 человека). Тогда 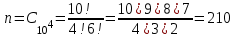 . .Число благоприятных для 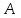 исходов равно исходов равно  . . ; ;Ответ: 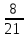 . .Задача №4. В промежутке между 12 и 22 часами к причалу независимо друг от друга должны прибыть для разгрузки два танкера. Один из этих танкеров разгружается в течение 4 часов, другой – в течение 6 часов. Найти вероятность того, что ни одному из танкеров не придется ждать освобождения причала другим. Задача №5. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что  -й станок потребует переналадку в течение смены равна -й станок потребует переналадку в течение смены равна 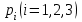 , р1 = 0,4, р2 = 0,5, р3 = 0,6. Найти вероятности следующих событий: , р1 = 0,4, р2 = 0,5, р3 = 0,6. Найти вероятности следующих событий:А – в течение смены 2 станка потребуют переналадку; В – ни один станок не потребует переналадки; С – хотя бы 1 станок потребует переналадку; D – не более 2-х станков потребуют переналадку. Решение. Введем обозначения: 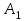 - первый станок потребует переналадку, - первый станок потребует переналадку, 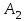 - второй потребует переналадку, - второй потребует переналадку, 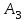 - третий потребует переналадку. Тогда, согласно определениям операций над событиями, имеем: - третий потребует переналадку. Тогда, согласно определениям операций над событиями, имеем: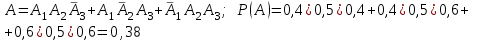  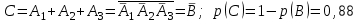 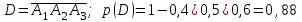 . .Ответ:  Задача №6. В партии деталей 30 % получены от завода №1, а остальные от завода №2. Из партии наудачу взяли деталь. Найти вероятность того, что взятая деталь стандартная, если брак на заводе №1 – 0,2, а на заводе №2 – 0,5. Взятая деталь оказалась с браком. Найти вероятность того, что эта деталь получена от завода №2. Введем обозначения: 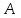 - взятая деталь стандартная, - взятая деталь стандартная,  - деталь получена от завода №1, - деталь получена от завода №1,  - деталь получена от завода № 2. По условию: - деталь получена от завода № 2. По условию:  По формуле полной вероятности: 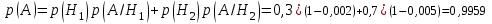 По формуле Байеса:  Ответ: 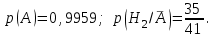 Задача №7. Контрольный тест содержит 10 вопросов, каждый из которых требует выбор правильного ответа из четырех данных, один из которых правильный, а остальные неправильные. Найти наиболее вероятное число правильных ответов, которое дает тестируемый, знающий 6 вопросов. Найти вероятность того, что тестируемый дает наиболее вероятное число правильных ответов. Решение. Пусть 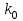 - наиболее вероятное число правильных ответов, которое даст тестируемый, отвечая наудачу на 4 вопроса теста, которых он не знает. Тогда общее число наиболее вероятного числа правильных ответов будет - наиболее вероятное число правильных ответов, которое даст тестируемый, отвечая наудачу на 4 вопроса теста, которых он не знает. Тогда общее число наиболее вероятного числа правильных ответов будет 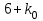 . Итак, найдем . Итак, найдем 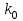 : : - целое, следовательно, - целое, следовательно, 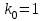 или или 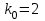 . Поэтому . Поэтому  или или 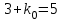 . Это означает, что . Это означает, что 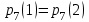 и искомая вероятность равна: и искомая вероятность равна: 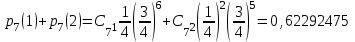 . .Ответ: 4 или 5; 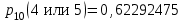 . .
Задача №8. Стрелок производит 4 выстрела по движущейся мишени. Вероятность попадания при  -м выстреле равна -м выстреле равна 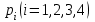 , p1 = 0,2, p2 = 0,3, p3 = 0,4, p4 = 0,5 , p1 = 0,2, p2 = 0,3, p3 = 0,4, p4 = 0,5Найти вероятности следующих событий: A – стрелок попадает в мишень ровно 2 раза; B - стрелок попадет в мишень хотя бы один раз; C – стрелок ни разу не попадет в мишень. Решение. Вероятность промаха при первом выстреле 0,6; при втором – 0,7; при третьем – 0,8 и при четвертом выстреле 0,9. Составим производящую функцию (многочлен) 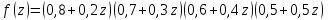 . .Если раскроим скобки, сделаем приведение подобных членов и запишем многочлен по возрастающим степеням, то вероятность  попаданий будет равна коэффициенту при попаданий будет равна коэффициенту при  . Итак: . Итак:  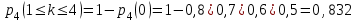 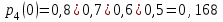 . .Ответ:  Задача №9. Игральная кость подбрасывается 4 раза. Найти вероятность того, что  очков выпадет 1 очко выпадает 2 раза, 2 очка – 1 раз и 3 очка – 1 раз.. очков выпадет 1 очко выпадает 2 раза, 2 очка – 1 раз и 3 очка – 1 раз..
Задача №10. 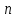 станков работают независимо друг от друга, причем вероятность бесперебойной работы каждого станка в течение смены равна станков работают независимо друг от друга, причем вероятность бесперебойной работы каждого станка в течение смены равна 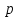 .Найти вероятность того, что в течение смены бесперебойно проработают: .Найти вероятность того, что в течение смены бесперебойно проработают: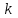 станков; станков;от 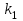 до до  станков. станков.
Задача №11. На торговую базу завод отправил 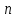 бутылок минеральной воды. Вероятность повреждения при транспортировке для каждой бутылки равна бутылок минеральной воды. Вероятность повреждения при транспортировке для каждой бутылки равна 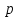 . Найти вероятность повреждения при транспортировке: . Найти вероятность повреждения при транспортировке: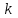 бутылок; бутылок;от 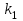 до до  бутылок; бутылок;более 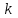 бутылок. бутылок.
Задача №12. Найти закон распределения случайной величины  - числа изделий высшего сорта среди - числа изделий высшего сорта среди 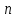 наудачу извлеченных из коробки изделий, если в коробке наудачу извлеченных из коробки изделий, если в коробке 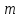 изделий, среди которых изделий, среди которых 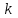 изделий высшего сорта. Найти изделий высшего сорта. Найти 
Задача №13. Мишень разделена на три зоны: I, II, III. За попадание в зону I дается 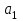 очков, в зону II - очков, в зону II - 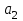 очков и в зону III - очков и в зону III -  очков. Для данного стрелка вероятности попадания в зоны I, II, III соответственно равны очков. Для данного стрелка вероятности попадания в зоны I, II, III соответственно равны  . Найти закон распределения случайной величины . Найти закон распределения случайной величины  , равной числу заработанных очков стрелком при двух независимых выстрелах по мишени. Найти , равной числу заработанных очков стрелком при двух независимых выстрелах по мишени. Найти  . .
|

 +BC
+BC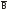 +AC
+AC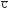 +AB
+AB