Билеты математика. билеты матан. Вопрос 22. Случайное событие, виды событий, действия над событиями
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Вопрос 22. Случайное событие, виды событий, действия над событиями. Случайными событиями мы будем называть любое явление, которое может происходить вокруг нас (или не происходить). События называются несовместными, если появление одного из них исключает появление других. Несовместные, т.е. события, которые не могут произойти одновременно. Теорема: Если события А и В несовместны, то их произведение есть невозможное событие. Достоверным событиемназывается событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. Действия над событиями. 1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произойдет либо событие А, либо событие В, либо, если это возможно, они произойдут одновременно. 2. Произведением А*Всобытий А и В называется событие, состоящее в том, что события А и В произойдут одновременно. 3. Разностью А\В событий А и В называется событие, состоящее в том, что произойдет та часть события А, которая не входит в В. Сумма события – операция «ИЛИ» Произведение события- операция «И» Переход к противоположному- операция «НЕ» СВОЙСТВА ОПЕРАЦИЙ A+ A = A A · A = A A+B = B + A (A+B) + C = A+ (B + C) A+ Ω = Ω A · Ω = A AB = BA A · ∅ = ∅ A(B + C) = AB + AC A+ (BC) = (A+B)(A+ C) A+ A = Ω A+ ∅ = A A+B = AB A ·B = A+B Вопрос 23. Классическое определение вероятности, статистическое определение вероятности, геометрическое определение вероятности Вероятность события равна отношению числа случаев , благоприятствующих ему, из общего числа единственно возможных, равновозможных и несовместных случаев к числу 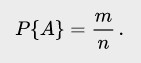 Частота появления событий при многократно повторяющихся Опытах имеет тенденцию стабилизироваться около какой-то постоянной величины. Таким образом, с рассматриваемым событием можно связать некоторую постоянную величину, около которой группируются частоты и которая является характеристикой объективной связи между комплексом условий, при которых проводятся опыты, и событием. Вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний. Это определение вероятности называется статистическим. вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности. Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3. Вероятность невозможного события равна нулю. Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей. Вопрос 24. Совместные и несовместные, зависимые и независимые события. Условная вероятность. Теоремы сложения и умножения вероятности. События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое. Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны. События называются совместными, если наступление одного из них не исключает наступления другого. Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события. Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми. Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события. P(А+B)=P(A)+P(B)-P(A*B) Вероятность двух событий равна сумме вероятностей этих событий минус вероятность их произведения Вероятность суммы несовместных событий равна сумме вероятностей этих событий. P(A)=1-P(A*) Вероятность наступления события равна единице минус вероятность ненаступления события Пусть с испытаниями связаны события А,Б. запись P(B/A)означает вероятность события B при условии, что А наступило P(B/A)-условная вероятность P(A*B)=B(A)*P(B/A) вероятность произведения двух событий равна вероятности одного из них, умноженного на вероятность другого при условии, что первое наступило. Операции над событиями: Сумма событий несовместные P(A+B)=P(A)+P(B) совместные P(A+B)=P(A)+P(B)-P(A*B) произведение событий независимые P(A*B)=P(A)*P(B/A) Вопрос 25. Формула полной вероятности. Формула Байеса Пусть событие а может наступить при условии появления 1 из несовместимых событий h1,h2,h3…. Которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности P(H1/A)…события А ТЕОРЕМА: вероятность события а, которое может наступить лишь при условии появления 1 из несовместных событий h1,h2,hn образуюих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события а P(A)=P(H1)*P(A/H1)+P(H2)*P(A/H2)…    Формула Байеса   Вопрос 26. Схема с повторениями испытаний(схема Бернулли). Формула Бернулли. Теорема Пуассона. Проводится серия н независимых испытаний. Независимость испытаний означает, что при выполнении каждого следующего испытания полностью восстанавливается комплекс условий, при которых выполнялось предыдущее испытание При каждом испытании интересующее нас событие А(успех) наступает в вероятность р и не наступает с вероятностью g=1-р ФОРМУЛА БЕРНУЛЛИ  Пример 1. Проводится 10 независимых бросаний монеты. Вероятность того, что 3 раза из 10 выпадет герб P=g=1/2, n=10, k=3 Pn(k)=сочетание из 10 по 3 *(1/2)^3*(1/2)^7=15/128 ТЕОРЕМА ПУАССОНА Если вероятность р наступление события а в каждом испытании стремится к нулю при неограниченном увеличении числа н испытаний, причём произведение нр стремится к постоянному числу лямбда, то вероятность того, что событие а появится к раз в н независимых испытаниях, удовлетворяет предельному равенству  Вопрос 27. Повторные независимые испытания. Локальная и интегральная формулы Муавра-Лапласа Повторные независимые испытания На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие . При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа появлений события в результате испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события в каждом испытании постоянна. Такие испытания называются повторными независимыми. Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом. Локальная формула 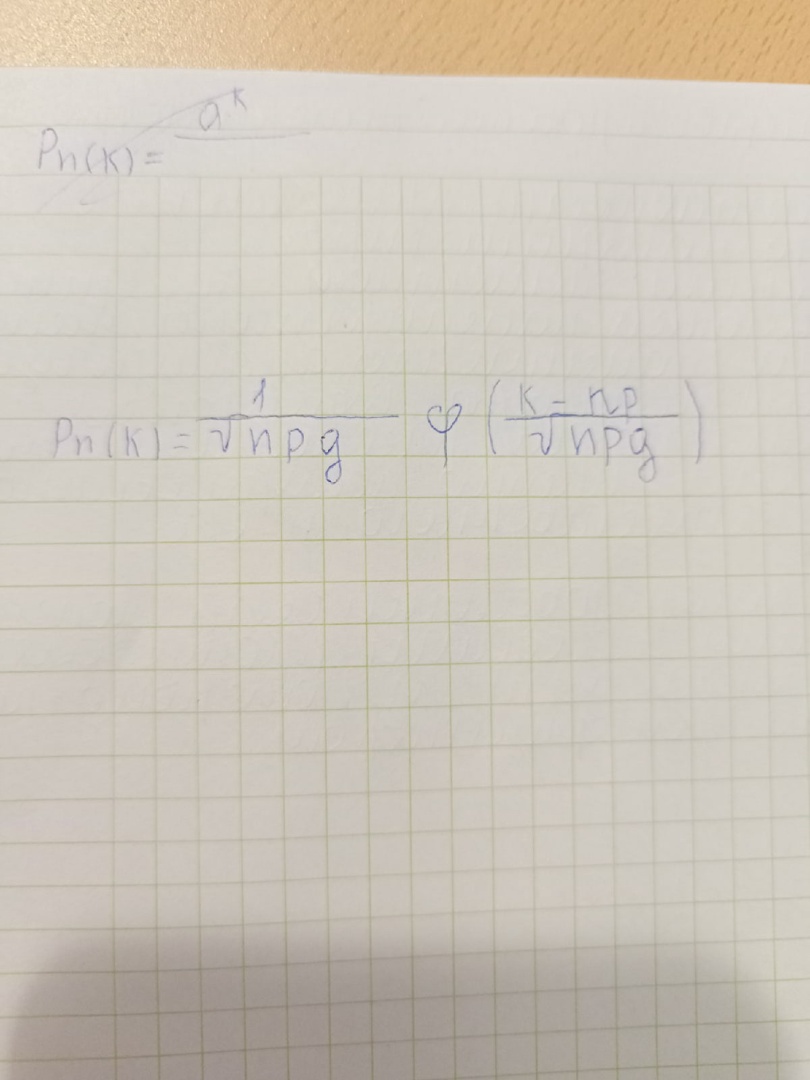 Интегральная формула 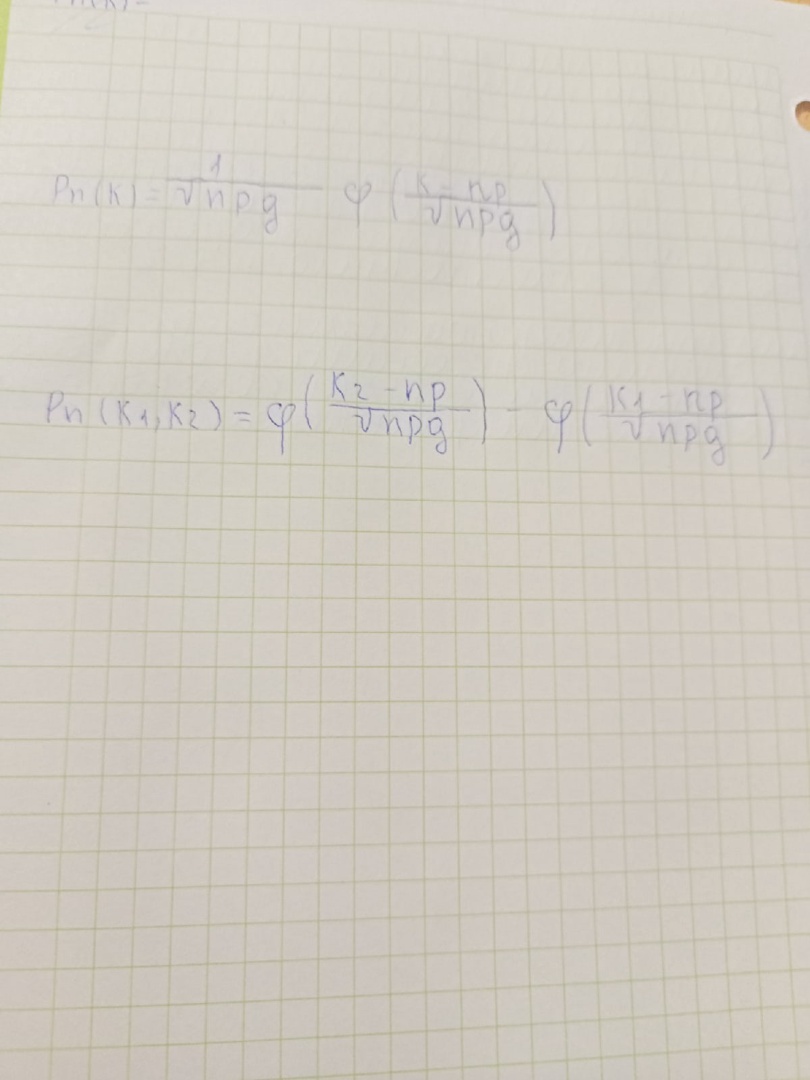 Вопрос 28. Случайная величина. Виды случайных величин. ЗРВДСВ. случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое. Дискретные и непрерывные величины Дискретная величина, величина, принимающая отдельные, изолированные друг от друга возможные значения с определённой вероятностью Число возможных значений дискретной случайной величины может быть КОНЕЧНЫМ и БЕСКОНЕЧНЫМ. Непрерывная- величина, которая принимает все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. ЗРВДСВ называют соответствие между возможными значениями и их вероятность( табличный, аналитический, графический) При табличном значении первая строка- возможные значения, вторая- их вероятности.
P1+p2+…=1 Если множество возможных значений бесконечно, то ряд p1,p2 сходятся и его сумма=1 Пример: В денежной лотерее выпущено 100 билетов. Разыгрывается 1 выигрышный билет стоимостью 50 р. И десять выигрышных билетов стоимостью в 1 р. Найти ЗРСВ х- стоимости возможного выигрыша.
P1+p2+p3=1 0,01+0,1+0,89=1 ЗРДСВ х может быть задан аналитически P(x=xi)= фи(xi)или с помощью функции распределения Вопрос 29. Закон распределения вероятностей дискретной случайной величины. Биноминальное распределение и его числовые характеристики. |
