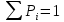Совместное распределение. Совм.расп. Совместный закон распределения

• Название: Совместный закон распределения
• Анкор: Совместное распределение
• Дата: 15.06.2021
• Размер: 23.2 Kb.
• Имя файла: Совм.расп.docx
• Тип: Закон; #217448

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Омский государственный технический университет»

Факультет информационных технологий и компьютерных систем

Кафедра «Автоматизированные системы обработки информации и управления»

ДОМАШНЕЕ ЗАДАНИЕ

по дисциплине «Математика»

на тему

«Совместный закон распределения»

23 вариант

Выполнил:

ст.гр. ПИН – 191

А.Ю. Судакова

Принял:

доцент

Г.А. Троценко

Омск 2021

Задание

В приведенной ниже задаче на основе заданного распределения случайной точки (ξ₁, ξ₂) найти:

1) одномерные законы распределения случайных величин ξ₁, ξ₂ и их числовые характеристики;

2) коэффициент корреляции случайных величин ξ₁, ξ₂.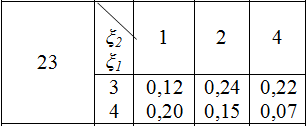

Решение

Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:

P(X=x_i, Y=y_j) = p_ij, i=1, 2..., n, j=1, 2.., m

Ряд распределения Х:

x	3	4
P	0.58	0.42

Математическое ожидание M[X]:
M[X] = 3*0.58 + 4*0.42 = 3.42

Дисперсия D[X]:
D[X] = 3²*0.58 + 4²*0.42 - 3.42² = 0.24

Среднее квадратическое отклонение σ(x):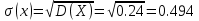

Ряд распределения Y:

y	1	2	4
P	0.32	0.39	0.29

Математическое ожидание M[Y].
M[Y] = 1*0.32 + 2*0.39 + 4*0.29 = 2.26

Дисперсия D[Y].
D[Y] = 1²*0.32 + 2²*0.39 + 4²*0.29 - 2.26² = 1.41

Среднее квадратическое отклонение σ(x):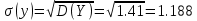



Поскольку, P(X=3,Y=1) = 0.12≠0.58•0.32, то случайные величины X и Y зависимы.

Ковариация:

cov(X,Y) = M[X*Y] - M[X]*M[Y]

cov(X,Y) = 1*3*0.12 + 2*3*0.24 + 4*3*0.22 + 1*4*0.2 + 2*4*0.15 + 4*4*0.07 - 3.42*2.26 = -0.17

Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X,Y) ≠ 0.

Коэффициент корреляции: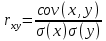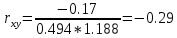