Имитационная модель многоядерного процессора. Современные вычислительные системы по способу построения аппаратной части делятся на сосредоточенные и распределенные. Первые, в свою очередь, могут быть одномашинными или комплексами многомашинными и многопроцессорными
 Скачать 332.77 Kb. Скачать 332.77 Kb.
|
1 2 ВВЕДЕНИЕ Современные вычислительные системы по способу построения аппаратной части делятся на сосредоточенные и распределенные. Первые, в свою очередь, могут быть одномашинными или комплексами: многомашинными и многопроцессорными. Распределенные ВС характеризуются большой длиной каналов связи между устройствами и подразделяются на системы с телекоммуникационным доступом и сети. Сети компьютеров представляют собой полностью распределенные системы. По масштабу и составу ЭВМ различают локальные и кампусные сети, а также сети мегаполисов и глобальные. Современные компьютеры имеют Неймановскую архитектуру и работают в одно- или мультипрограммном режиме. Последний позволяет повысить их производительность и характеризуется коэффициентом мультипрограммирования, который равен среднему количеству одновременно выполняемых программ. В теории вычислительных систем формируются и решаются три класса задач: анализа, развития и проектирования. Задачи анализа связаны с разработкой моделей, позволяющих определить зависимость характеристик от параметров системы. При решении задач развития и проектирования используются модели, разработанные для анализа. Причем задача проектирования обычно формулируется как задача оптимизации. Ее сложность не позволяет решить эту задачу в общем случае. В теории вычислительных систем используются два класса методов исследования: экспериментальные и модельные. Экспериментальные методы исследования вычислительных систем помогают получить наиболее достоверные сведения об объекте, но при этом достаточно трудоемки и имеют частный характер результатов. В модельных методах исследования используются два класса моделей: аналитические и имитационные. Аналитические модели просты в исполнении, но характеризуются большими погрешностями. Имитационные модели описывают поведение объекта с помощью алгоритмических методов. Главное преимущество этих моделей – универсальность. Они позволяют исследовать объекты любой сложности и с любым уровнем детализации. Имитационные модели используются для изучения сложных систем. Для лучшего усвоения материала в них применяется анимация. Высокая сложность элементов и устройств вычислительных систем, а также интегральные технологии, используемые при их производстве, затрудняют изучение их структур и режимов работы непосредственно на объектах. Альтернативой является имитационное моделирование, которое позволяет воспроизвести наиболее важные аспекты структуры и функционирования вычислительных систем и отбросить второстепенные факторы. Целью предлагаемого дипломного проекта является разработка имитационных моделей типового многоядерного процессора, работающего в одно- и мультипрограммном режиме. Указанная цель достигается: Выбором структуры модели; Определением уровня детализации параметров; Разработкой алгоритмов и программ имитационного моделирования. Программа будет включена в пакет, который предназначен для проведения лабораторных работ по дисциплине «Аппаратные средства вычислительной техники». В процессе дипломного проектирования предстоит решить следующие задачи: проанализировать предметную область; выбрать структуру процессора, которую нужно отобразить в модели; выбрать уровень детализации параметров структуры; разработать структуру имитационной модели двухъядерного процессора; произвести тестирование разработанной системы. Актуальность и практическая значимость предлагаемой работы заключаются в решении проблем организации лабораторного практикума по дисциплине «Аппаратные средства вычислительной техники», которая впервые вводится в учебный процесс. 1 Методы и средства исследования вычислительных систем 1.1 Типовые структуры современных процессоров и режимы их работы Центральный процессор (CPU) – это главный рабочий компонент компьютера, выполняющий машинные инструкции (арифметические и логические операции), заданные программой. Он управляет вычислительными процессами и координирует работу аппаратного обеспечения компьютера. Типовой центральный процессор, в общем случае, состоит из следующих элементов: арифметико-логическое устройство; блок управления; регистры; счетчики команд; кэш. Укрупненная структура процессора представлена на рисунке 1.1. Арифметико-логическое устройство (АЛУ) – блок процессора, предназначенный для выполнения логических и арифметических операций, то есть преобразования информации. Регистр – устройство, служащее для временного хранения управляющей информации, операндов и/или результатов выполняемых операций. Счетчик команд (СК) – регистр, который, в зависимости от архитектуры, хранит в себе адрес текущей выполняемой команды или команды, которая будет выполняться. СК обеспечивает автоматический переход к следующей команде программы из последовательных ячеек памяти Регистр команд (РК) – регистр, содержащий в себе выполняемую команду. Блок управления (БУ) – устройство, задачей которого является формирование очереди управляющих сигналов, которые посылаются на все блоки центрального процессора, и обеспечивают выполнение очередной команды и переход к следующей. 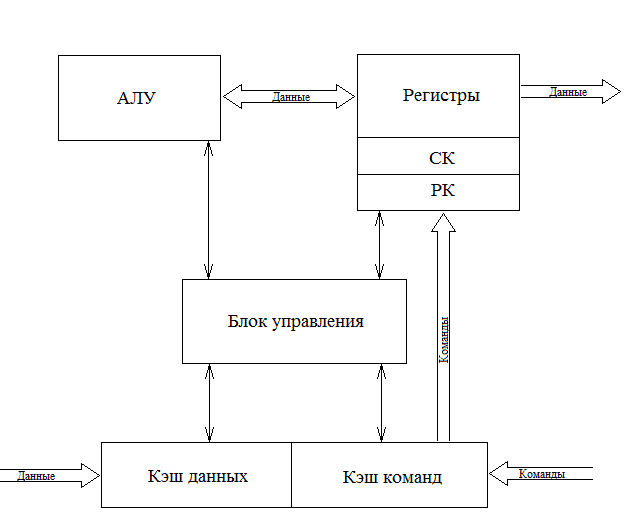 Рисунок 1.1 – Укрупненная структура центрального процессора. В современных центральных процессорах кэш, как правило, делится на два блока: команд и данных. Первый используется для более быстрой загрузки команд машинного кода. Кэш данных применяется для быстрого чтения и записи данных. Данный кэш центрального процессора разделён на несколько уровней. В большинстве современных универсальных процессоров в настоящее время используется до трех уровней. Иерархия уровней кэша данных идёт от самого маленького и быстрого (L1) и затем переходит к большим и более медленным кэшам (L2 и затем L3). L1-кэш – это самая быстрая память, которая является неотделимой частью центрального процессора, так как располагается в том же кристалле что и процессор и служит частью функциональных блоков. Зачастую процессоры не способны функционировать без L1-кэша. Данный кэш работает параллельно с центральным процессором и на одной с ним частоте, поэтому обращение к нему может производиться на каждом такте. Конвейерная архитектура центрального процессора является одной из наиболее широко распространенных архитектур. Конвейерный принцип используется для повышения быстродействия процессора. Суть данной архитектуры заключается в том, что центральный процессор может работать над несколькими командами одновременно, разделяя их на микрооперации и выполняя разные микрооперации разных команд одновременно. В каждом такте команда в конвейере продвигается на следующую микрооперацию. Если в команде выполнилась последняя микрооперация, то эта команда заменяется следующей в конвейере. Известно, что типичную арифметическую команду можно разделить на следующие микрооперации: IF (Instruction Fetch ) – выборка команд из памяти (по адресу в счётчике команд); ID ( Instruction Decoding ) – декодирование кода операции; OR (Operand Reading ) – выборка операндов из регистров; EX (Executing ) – выполнение операции в АЛУ; WB (Write Back ) – запоминание результата в регистре. Выполнение команд в конвейере представлено на рисунке 1.2. Длительность одного такта процессора задаётся в соответствии с максимальным временем выполнения всех микроопераций в конвейере, поскольку в течении такта обычно выполняются различные этапы обработки команд. При этом учитывается, что для перехода команды с одной стадии на другую тратится дополнительное время ( 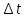 ), в течение которого промежуточные результаты записываются в буферные регистры. ), в течение которого промежуточные результаты записываются в буферные регистры. 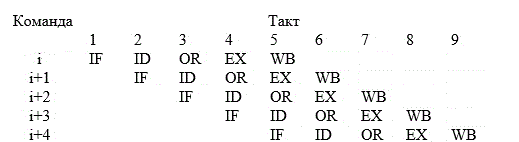 Рисунок 1.2 – Выполнение микроопераций в конвейере При анализе рисунка 1.2 можно увидеть, что во время конвейерной обработки после того, как получен результат выполнения первой команды, результат второй появляется в следующем такте работы процессора. Время выполнения команд в конвейере рассчитывается по формуле При этом среднее время выполнения одной команды При N→∞, Тср→T, т.е. конвейером выполняется одна команда за такт. Существенное превосходство конвейерного принципа обработки перед последовательным имеет место в идеальном конвейере, когда все микрооперации имеют одинаковую продолжительность. Когда данное условие нарушается, производительность конвейера начинает снижаться, поскольку некоторые устройства начинают простаивать. Ситуации, которые препятствуют очередной команде из потока выполняться в предназначенном для нее такте, называются конфликтами в конвейере. Их наличие может значительно снижать настоящую производительность центрального процессора по сравнению с идеальной ситуацией. Существует три типа конфликтов. структурные, которые возникают из-за занятости отдельных ресурсов (когда аппаратные средства не могут поддерживать выполнение команд в режиме с совмещением); по данным, появляющиеся, если выполнение очередной команды зависит от результата предыдущей; по управлению, которые возникают при наличии команд переходов и команд, изменяющих значение счетчика команд. Возникновение конфликтов приводит к задержке выполнения команды, во время выполнения которой они возникли. Такая ситуация называется «конвейерным пузырем», в течение которого на конвейере не выполняется никакая работа. Существуют разнообразные методы борьбы с перечисленными конфликтами. Для устранения структурной коллизии стараются уменьшить количество кэш-промахов за счет увеличения объема кэша, а также используют раздельную память команд и данных и другие средства. Конфликты по данным устраняются с помощью оптимизирующих компиляторов или аппаратных средств микропроцессоров, которые изменяют порядок выполнения команд в программе. Другим путем ликвидации этих коллизий является расширение регистровой и кэш памяти, в частности, создание регистровых файлов, у которых запись данных производится в разные ячейки. Конфликты по управлению устраняются за счет дублирования ветвей, а также использования так называемого отсроченного или прогнозируемого перехода. В настоящее время широко применяется суперконвейризация, которая увеличивает количество ступеней конвейеров. При этом каждая отдельная ступень исполняет меньшую работу и, следовательно, содержит меньше аппаратной логики. Увеличение простоты логики уменьшает задержку распространения сигнала. Благодаря этому становится возможным повышение тактовой частоты. Стремление увеличить производительность центрального процессора привело к включению в состав АЛУ нескольких параллельно работающих конвейеров. Для того чтобы обеспечить оптимальную загрузку такой системы, в каждом такте формируется пакет команд, длина которого равна числу конвейеров. Пакет может быть получен одним из двух способов: динамически, в процессе выполнения программы, причем размер пакета зависит от положения конфликтов в программе; до выполнения программы, с помощью компилятора. Первый способ используется в суперскалярных, а второй – в VLIW процессорах. Суперскалярная архитектура центрального процессора на сегодняшний день является наиболее распространенной. Центральный процессор имеет два и более конвейеров, что позволяет исполнять несколько команд в течение каждого такта. Общая структура суперскалярного процессора представлена на рисунке 1.3. 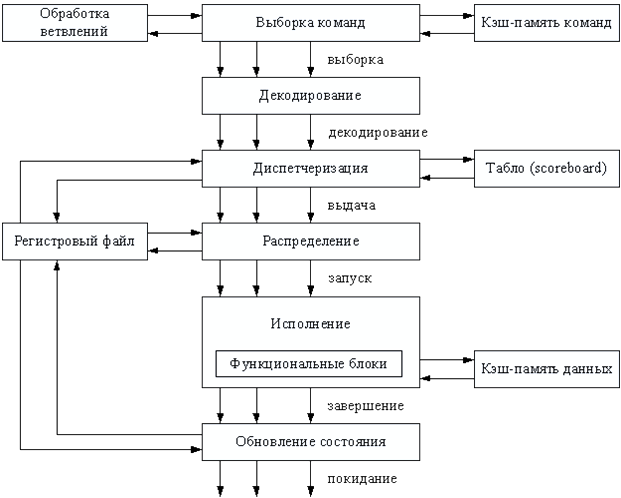 Рисунок 1.3 – Структура суперскалярного процессора. Блоки суперскалярного процессора выполняют следующие функции: Блок выборки команд используется для извлечения команды из кэша, хранения очереди выбранных команд и обработки команды условного перехода; Блок декодирования дешифрирует код операции, заключающийся в извлеченных из кэш-памяти командах; Блоки диспетчеризации и распределения взаимодействуют друг с другом и в совокупности исполняют в суперскалярном процессоре роль контроллера трафика. Оба блока хранят очереди расшифрованных команд. Очередь блока распределения зачастую разделяется на несколько независимых буферов – накопителей команд или схем резервирования (reservation station), – предназначенных для сохранения команд, которые уже расшифрованы, но еще не  Рисунок 1.4 – Конвейер выборки и декодирования. Рисунок 1.4 – Конвейер выборки и декодирования.реализованы. Все накопители команд связаны со своим функциональным блоком (ФБ), поэтому количество накопителей обычно равно числу функциональных блоков, но если в процессоре применяется несколько однотипных функциональных блоков, то им придается общий накопитель. По отношению к блоку диспетчеризации накопители команд выполняют роль виртуальных функциональных устройств. В дополнение к очереди блок диспетчеризации сохраняет список неиспользуемых ФБ, который называется табло. Табло применяется для отслеживания состояния очереди распределения. Один раз за цикл блок диспетчеризации достает команды из своей очереди, считывает из памяти или регистров операнды этих команд, после чего табло отправляет команды и значения операндов в очередь распределения. Этот процесс называется выдачей команд. Блок распределения в каждом цикле исследует все команды в своих очередях на присутствие всех нужных для их исполнения операндов и при утвердительном результате приступает к исполнению этих команд в соответствующем ФБ. Блок исполнения содержит в себе комплект функциональных блоков. Образцами ФБ могут быть целочисленные операционные блоки, блоки умножения и сложения с плавающей запятой, блок доступа к памяти. Когда реализация команды завершается, полученный результат сохраняется и используется блоком обновления состояния, который позволяет учитывать сохранённый результат теми командами в очередях распределения, где данный результат является одним из операндов. Каждый из блоков процессора в свою очередь, как правило, построен в виде конвейера. Как было отмечено ранее, суперскалярность предполагает параллельную работу максимального числа исполнительных блоков, что возможно лишь при одновременном выполнении нескольких скалярных команд. Последнее условие хорошо сочетается с конвейерной обработкой, при этом желательно, чтобы в суперскалярном процессоре было несколько конвейеров, например два или три. Подобный подход реализован в микропроцессоре Intel Pentium, где имеются два конвейера, каждый со своим АЛУ (рисунок 1.4). Отметим, что здесь, в отличие от стандартного конвейера, в каждом цикле необходимо производить выборку более чем одной команды. Соответственно, память ВМ должна допускать одновременное считывание нескольких команд и операндов, что чаще всего обеспечивается за счет ее модульного построения. 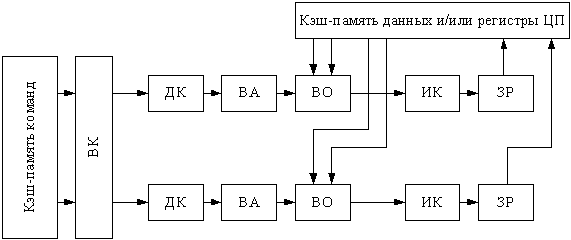 Рисунок 1.5 – Суперскалярный процессор с двумя конвейерами. По разным оценкам, применение суперскалярного подхода приводит к повышению производительности ВМ в пределах от 1,8 до 8 раз. Основным достоинством суперскалярных процессоров является возможность выполнения исполняемого модуля программы в любой модели процессора. Недостатком таких процессоров является сложность управления процессом выполнения программы, поскольку формирование пакета команд и устранение конфликтов выполняется динамически. В отличие от суперскалярной архитектуры, в процессорах архитектуры VLIW (very long instruction word – «очень длинная машинная команда») оптимизирующий компилятор создаёт такой код, в котором отсутствуют конфликты или их количество сведено к минимуму. Код точно указывает, когда будет выполнена каждая операция, какие функциональные устройства будут работать и какие регистры будут содержать операнды. Компилятор VLIW создаёт такой план выполнения, имея полное представление о процессоре VLIW, причём создаёт этот план так, чтобы добиться требуемой записи выполнения – последовательности событий, которые действительно происходят во время работы программы. Компилятор передаёт план выполнения (через архитектуру набора команд, которая точно описывает параллелизм) аппаратному обеспечению, которое, в свою очередь, выполняет этот план. Процессоры VLIW представляют собой пример архитектуры, для которой программа представляет точную информацию о параллелизме. Компилятор выявляет параллелизм в программе и сообщает программному обеспечению, какие операции не зависят друг от друга. Эта информация имеет важное значение для аппаратного обеспечения, поскольку в этом случае оно «знает» без дальнейших проверок, какие операции можно начинать выполнять в одном и том же такте. Достоинства VLIW заключаются в следующем: Компилятор может эффективнее исследовать зависимости между командами и выбирать параллельно исполняемые команды, чем это делает аппаратура суперскалярного процессора, ограниченная размером окна исполнения. VLIW процессор имеет более простое устройство управления и потенциально может иметь более высокую тактовую частоту. Недостатком этих процессоров является то, что исполняемый код программы зависит от структуры процессора (от числа конвейеров). Поэтому программу приходится компилировать заново для новых моделей процессоров. Одной из перспективных считается архитектура центральных процессоров с явно выраженным параллелизмом команд (EPIC – Explicitly Parallel Instructions Computer), которая сочетает в себе принципы как суперскалярной, так и VLIW–обработки. Первым представителем такой структуры был микропроцессор Itanium компании Intel. EPIC позволяет микропроцессору реализовывать инструкции параллельно, опираясь на работу компилятора, а не обнаруживая возможность параллельной работы инструкций с использованием специальных схем. Это помогло увеличить вычислительную мощность центрального процессора, не увеличивая тактовую частоту. В архитектуре EPIC команды группируются компилятором в сверхдлинную группу (длиной в 128 разрядов). Логика выдачи команд на исполнение сложнее, чем в традиционных процессорах типа VLIW, но намного проще, чем у суперскалярных с неупорядоченной выдачей. В центральных процессорах типа EPIC конфликты по данным и часть структурных устраняются на этапе компиляции, а коллизии по управлению и промахи при обращении к кэш памяти – динамически. Данный подход делает механизм и схему управления вычислениями заметно проще. Время, затрачиваемое на этот процесс, укорачивается, а эффективность системы повышается. EPIC упрощает два ключевых момента, реализуемых во время выполнения. Во-первых, его принципы позволяют во время исполнения отказаться от проверки зависимостей между операциями, которые компилятор уже объявил как независимые. Во-вторых, данная архитектура позволяет отказаться от сложной логики внеочередного исполнения операций, полагаясь на порядок выдачи команд, определенный компилятором. Более того, EPIC совершенствует возможность компилятора статически генерировать планы выполнения за счет поддержки разного рода перемещений кода во время компиляции, которые были бы некорректными в последовательной архитектуре. Более ранние решения достигали этой цели главным образом за счет серьезного увеличения сложности аппаратного обеспечения, которое стало настолько значительным, что превратилась в препятствие, не позволяющее отрасли добиваться еще более высокой производительности. EPIC разработан именно для того, чтобы обеспечить более высокую степень параллелизма на уровне команд, поддерживая при этом приемлемую сложность аппаратного обеспечения. Более высокая производительность достигается как за счет увеличения скорости передачи сигналов, так и благодаря увеличению плотности расположения функциональных устройств на кристалле. Зафиксировав рост этих двух составляющих, дальнейшего увеличения скорости выполнения программ можно добиться в первую очередь благодаря реализации определенного вида параллелизма. Так, параллелизм на уровне команд (ILP — Instruction-Level Parallelism) стал возможен благодаря созданию процессоров и методик компиляции, которые ускоряют работу за счет параллельного выполнения отдельных RISC-операций. Системы на базе ILP используют программы, написанные на традиционных языках высокого уровня, для последовательных процессоров, а обнаружение «скрытого параллелизма» автоматически выполняется благодаря применению соответствующей компиляторной технологии и аппаратного обеспечения. Тот факт, что эти методики не требуют от прикладных программистов дополнительных усилий, имеет крайне важное значение, поскольку данное решение резко отличается от традиционного микропроцессорного параллелизма, который предполагает, что программисты должны переписывать свои приложения. Параллельная обработка на уровне команд является единственным надежным подходом, позволяющим добиться увеличения производительности без фундаментальной переработки приложения. Таким образом, в современных микропроцессорах широко используется конвейерная обработка. Для повышения их производительности применяют мульти- и суперконвейеризацию. Эффективная работа конвейера может быть нарушена из-за конфликтов. Стремление максимально повысить производительность процессора привело к использованию двух разных подходов к устранению конфликтов. Первый реализуется динамически, в процессе выполнения программы. Он характерен для суперскалярных процессоров. Устранение большинства конфликтов с помощью компилятора характерно для VLIW – процессоров. Наконец, процессоры EPIC используют сочетание обоих подходов. Несмотря на целый ряд недостатков, суперскалярные процессоры занимают лидирующее положение на рынке. Их важнейшим достоинством является независимость исполняемого кода программы от внутренней структуры процессора. Это позволяет выполнять одну и ту же программу на любой модели микропроцессора. 1.2 Задачи исследования вычислительных систем Основными задачами, решаемыми в рамках теории вычислительных систем являются: анализ; развитие; проектирование. Анализ – это установление свойств, характерных системе или классу систем. При анализе оцениваются характеристики вычислительной системы и строятся её модели. Отталкиваясь от цели исследования, устанавливают набор характеристик. Основными характеристиками вычислительной системы, которые исследуются во время анализа являются: производительность; время ответа; надежность. Производительность вычислительных систем общего назначения оценивается в зависимости от области применения номинальной, комплексной, системной производительностью и производительностью на рабочей нагрузке. Номинальная производительность характеризует только быстродействие, или производительность устройств, входящих в состав системы. Комплексная производительность учитывает не только быстродействие устройств, но и структуру системы – ее влияние на быстродействие совместно функционирующих устройств. Системная производительность учитывает как вышеназванные факторы – быстро действие устройств и структуру связей между ними, так и влияние операционной системы. Производительность на рабочей нагрузке (кратко – производительность) отображает все факторы, влияющие на системную производительность, и, кроме того, свойства рабочей нагрузки – задач, решаемых вычислительной системой. С производительностью тесно связана такая характеристика качества обслуживания пользователей, как время ответа, т.е. время пребывания задач в системе. Поэтому при оценке производительности определяется не только количество работы, выполняемое системой в единицу времени, но и время ответа для всего множества задач и отдельных классов задач. Производительность вычислительной системы проявляется, с одной стороны, в скорости обработки задач, а с другой – в степени использования ресурсов системы. Чем больше загружены ресурсы, тем выше производительность системы, и недогрузка ресурсов свидетельствует о наличии резервов для повышения производительности. Поэтому при анализе производительности системы оцениваются не только показатели производительности, но и показатели, характеризующие использование ресурсов. Производительность вычислительной системы связана с продолжительностью процессов обработки задач, которая зависит от трех факторов: 1) рабочей нагрузки; 2) конфигурации системы; 3) режима обработки задач. Эти три фактора в совокупности определяют порядок развития вычислительных процессов во времени, и первая задача анализа производительности сводится к порску компактных и информативных форм представления вычислительных процессов. Эти формы создают концептуальную (понятийную) основу для оценки функционирования вычислительных систем в процессе эксплуатации и при исследовании с помощью моделей производительности. Вторая задача анализа – создание моделей, позволяющих прогнозировать производительность систем для различной конфигурации, режимов обработки и, возможно, разной рабочей нагрузки. При анализе требуется найти способ оценки характеристик Y объекта с заданной погрешностью ∆, и на основе этого способа определить его характеристики. Оценка характеристик Y производится замером параметров функционирования с обработкой измерительных данных. При этом определяют набор измеряемых параметров, периодичность и длительность замеров. Для уменьшения затрат измеряют наименьшее число наиболее легко измеримых параметров X={x1,…,xM}, а искомые характеристики определяют косвенным методом с использованием зависимостей ym=m(X), m=1,…,M. Такие зависимости обладают или статистической природой, или их получают, используя фундаментальные закономерности теории вычислительных систем. При анализе разрабатываемых ВС для оценки характеристики Y необходимо обладать моделью F, устанавливающей зависимостьY=F(X) характеристик от параметров X, определяющих конфигурацию вычислительной системы, режим функционирования, а также рабочую нагрузку. Тогда решение задачи сводится к проведению ряда экспериментов, позволяющих дать ответы на интересующий вопросы. Точность оценки характеристик зависит от адекватности модели и погрешности изменения параметров X. Модель считается адекватной системе, если воспроизводит тенденцию изменения характеристик, т. е. их прирост или снижение при изменении конфигурации системы. Перед решением задачи развития происходит идентификация– это построение модели системы на основе априорных сведений о ее организации и результатов измерений. В качестве функциональных моделей могут использоваться различные математические системы – дифференциальные и алгебраические уравнения, сети массового обслуживания и др. Для определения ее параметров к вычислительной системе подключаются необходимые измерительные средства. Получаемые данные используются системой оценки параметров и характеристик для вычисления параметров X* и характеристик Y* системы, а также параметров модели A={an}. Система оценки представляет собой набор программ для обработки измерительных данных, реализующий методы оценки параметров и характеристик. Вычисленные значения параметров A вводятся в модель, полностью определяя ее. Значения параметров X* и характеристик Y* системы используются для проверки адекватности модели, т.е. оценки погрешности ∆ с которой она воспроизводит характеристики системы. Оценка производится путем сравнения значений характеристик Y=F(X*), порождаемых моделью, с зарегистрированными характеристиками Y* системы. При решении задачи развития используются модели, разработанные для анализа, и на основании оценки характеристик производительности, времени ответа и надежности вносятся предложения об изменении конфигурации ВС с целью улучшения ее работы. При этом вначале разрабатывается функциональная модель, т.е. выполняется функциональная идентификация. Модель строят с учетом особенностей функционирования системы. Затем выполняют параметрическую идентификацию, т.е. определяют параметры модели. Далее к системе подключают измерительные средства, и результаты измерений используют для оценки параметров модели. Измеренные значения используют для оценки адекватности модели. Если разность измеренных значений и параметров модели не превышает погрешность, то модель адекватна, и ее можно использовать для решения задач развития.  Рисунок 1.6 – Схема развития вычислительной системы. При проектировании систем применяются те же модели для определения структуры ВС, наилучшим образом сбалансированной с ее рабочей нагрузкой. Для решения задачи проектирования нужны следующие сведения о вычислительной системе: функция данной ВС; ограничения на ее характеристики (производительность, время ответа, надежность); критерий эффективности, устанавливающий способ оценки качества системы в целом. Результатами проектирования являются: – структура вычислительной системы; – режим обработки задач. Необходимо выбрать режим обработки данных и конфигурацию системы, удовлетворяющие заданным ограничением и оптимальные по критерию эффективности. Математически задача проектирования вычислительной системы формулируется следующим образом. Пусть Q = (q1, q2, … , qM) – вектор параметров, характеризующих класс задач A, решение которых является функцией системы; S = (s1, . . . , sN) – вектор параметров, характеризующий конфигурацию (структуру) системы; С = (с1, . . . , сR) – вектор параметров режима обработки; Y = (y1, . . . , yN) – вектор характеристик системы, связанный с параметрами задач Q, конфигурации S и режима обработки С зависимостью Y = F(Q, S, С); S = {Si} – множество возможных конфигураций вычислительных систем; C = {Cj} – множество возможных режимов обработки. Ограничения на параметры и характеристики системы z, . . . , z (Y X) представляются в виде z z, . . . , z z, где z, . . . , z - области допустимых значений соответствующих характеристик и параметров. Критерий эффективности системы представляется заданной функцией E = Ф(Y), зависящей от характеристик системы, которые в свою очередь предопределяются ее параметрами Y = F(, S, С). В установленных обозначениях задача проектирования вычислительной системы формулируется так: определить конфигурацию S и режим обработки C, максимизирующие эффективность системы max E = max Ф(Y) (1.3) SS, CC при выполнении ограничений z z, . . . , z z. (1.4) Таким образом, при исследовании вычислительных систем решаются задачи анализа, развития и проектирования. Для этого используются модели вычислительных процессов и системы в целом, которые позволяют определить их характеристики. 1.3 Методы исследования ВС При исследовании вычислительных систем обычно используются следующие два класса методов: экспериментальные; модельные; Экспериментальные методы основываются на получении данных о работе вычислительных систем в реальных или специально созданных условиях для оценки качества работы и обнаружения зависимостей между параметрами и характеристиками. Типовые задачи, разрешаемые с использованием экспериментальных методов – оценка производительности и надежности вычислительных систем, установление состава и количественных показателей рабочей нагрузки. Исследование вычислительных систем с использованием экспериментального метода выполняется в несколько этапов: формулирование цели исследования; разработка методики исследования, определяющей модель объекта, способ и средства замера, способ и средства обработки измерительных данных и интерпретации результатов измерений; измерение процесса функционирования объекта в реальных или специально создаваемых условиях; обработка и интерпретация измерительных данных. Экспериментальные методы позволяют приобрести наиболее надежные данные о вычислительных системах. В большинстве случаев эксперименты оказываются единственным источником получения данных о функционировании и свойствах вычислительных систем. К примеру, количественная оценка параметров рабочей нагрузки систем общего назначения осуществляется, в основном, экспериментальными методами. Особенно большое значение данный метод имеет при решении задач эксплуатации, поскольку улучшение конфигурации и режима функционирования систем не является возможным без применения измерительных данных, описывающих конкретные условия работы системы. Недостатками экспериментального метода являются большая трудоёмкость и время, затрачиваемые на эксперименты, а также зависимость результатов от конфигурации системы и режимов её работы. Модельные методы исследования вычислительных систем заключаются в построении одного из двух типов моделей: аналитических; имитационных; Аналитические модели вычислительных систем являются, по сути, математическими, представляющими физические параметры системы как математические объекты и связи между ними, проявляемые посредством математических операций. Математические модели выявляют фундаментальные свойства вычислительных систем и являются центральной частью теории вычислительных систем. Аналитические модели показывают связь между исходными данными (параметрами) Х и характеристиками Y в форме некоторой функции Y=F(X). Чем крупнее область определения Х, тем универсальнее и точнее оказывается модель. Подобные модели обеспечивают высокую точность лишь в ограниченном диапазоне параметров. Связь между характеристиками и параметрами может быть представлена в явной форме – с помощью выражений ym=fm(x1,…,xN), решаемых в отношении искомых величин, или же в неявной форме – с помощью уравнений Ф(Y, Х)=0, связывающих характеристики и параметры. Аналитические модели можно создать лишь для довольно элементарных систем. При этом принимаются допущения о свойствах и поведении описываемых объектов, к примеру, отсутствие связи некоторых факторов, линейность отдельных зависимостей, мгновенность переходов от одного состояния к другому и т. д. Но исследование на упрощенной модели позволяет получить лишь приблизительные результаты, с довольно высокой погрешностью. Подобным образом, аналитические модели, можно использовать только для изучения тех систем, в которых достоверны принятые допущения. Большое число систем недоступно для изучения математическими моделями из-за специфики их устройства. Преимущества аналитических моделей заключаются в следующих причинах: полученные формулы являются достоверными и строго доказуемыми; математические зависимости позволяют найти характеристики для всей области значений параметров X и включают информацию о поведении соответствующих систем при различных сочетаниях параметров. На основе подобных моделей можно определить эффекты, которые возникнут при модификации параметров; математические модели характеризуются наименьшей сложностью расчётов. Подобное свойство является крайне существенным при решении задач проектирования, поскольку осуществляемая при этом оптимизация связана с многократными вычислениями характеристик при разнообразных значениях параметров. Основа имитационных моделей заключается в изображении последовательности функционирования системы в форме алгоритма, называемого имитационной (алгоритмической) моделью. Данные модели используют для исследования процесса функционирования сложных систем. Для реализации этого метода разрабатывается специальный моделирующий алгоритм, в соответствии с которым в ЭВМ формируется информация, изображающая элементарные процессы изучаемой системы с учетом всех взаимосвязей и взаимных влияний. Моделирующий алгоритм создается с учетом логической структуры системы, последовательности выполняемых в ней процессов и основных состояний системы. При построении имитационных моделей широко используется агрегатный подход. Для моделирования заданного класса систем создается набор агрегатов Ф1,…,ФQ – элементов модели. Агрегаты могут соответствовать элементам систем, например, процессорам, оперативным запоминающим устройствам, каналам ввода–вывода, каналам передачи данных и другим, воспроизводя определенные аспекты их функционирования. В качестве агрегатов могут выступать математические объекты, с помощью которых генерируются и преобразуются необходимые процессы. Так, для моделирования систем на основе сетей массового обслуживания в качестве агрегатов представляются источники потоков заявок, системы массового обслуживания, узлы, управляющие распределением заявок по нескольким направлениям, и т.д. По существу, агрегат – описание функции некоторого объекта в аспектах, соответствующих цели моделирования – оценке производительности, надежности и т. д. Функции агрегатов Ф1,…,ФQ представляются в параметрической форме, т. е. в записи функций используются параметры, характеризующие конкретный объект. Так, параметром процессора является производительность (быстродействие), оперативной памяти – емкость, системы массового обслуживания– дисциплина обслуживания, число каналов и распределение длительности обслуживания. Функция агрегата Фq,q=1,…,Q , представляется в алгоритмической форме – в виде процедуры Фq=(a1,…,ak,b1,…,bi,c1,…,cm), где параметры a1,…,ak – определяют состояние входов элемента, b1,…,bi – режим его функционирования и c1,…,cm – состояние выходов элемента. Сколь ни была бы сложна функция агрегата Фq, в модели агрегат выглядит как элемент (рисунок 1.7), настраиваемый на заданный режим функционирования множеством параметров Bq={b1,…,bi} и преобразующий входные воздействия Aq={a1,…,ak} в выходные состояния Cq={c1,…,cm} в соответствии с функцией агрегата Фq и значениями параметров Bq. Множество агрегатов разного типа {Ф1,…,ФQ} составляет базис имитационных моделей заданного класса систем.  Рисунок 1.7 – Агрегат, как элемент модели. Имитационная модель собирается из агрегатов путем соединения выходов агрегатов с входами других агрегатов (рисунок 1.8).  Рисунок 1.8 – Агрегатная модель. На рисунке агрегаты обозначены 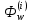 , где w – тип и i –порядковый номер агрегата в модели. Агрегаты , где w – тип и i –порядковый номер агрегата в модели. Агрегаты 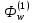 и и 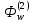 – генераторы, формирующие воздействия в соответствии с параметрами В1и В2. Состав агрегатов, структура связей между ними и наборы параметров агрегатов В1,...,В6 определяют модель. Процесс моделирования состоит в реализации процедур – генераторы, формирующие воздействия в соответствии с параметрами В1и В2. Состав агрегатов, структура связей между ними и наборы параметров агрегатов В1,...,В6 определяют модель. Процесс моделирования состоит в реализации процедур 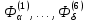 в необходимом порядке. При этом значения, формируемые на выходах агрегатов, переносятся на входы связанных с ними агрегатов, в результате чего вычисляются значения z1и z2. Путем обработки данных, наблюдаемых в характерных точках модели (на выходах элементов), получают оценки качества функционирования любого из агрегатов и системы в целом. в необходимом порядке. При этом значения, формируемые на выходах агрегатов, переносятся на входы связанных с ними агрегатов, в результате чего вычисляются значения z1и z2. Путем обработки данных, наблюдаемых в характерных точках модели (на выходах элементов), получают оценки качества функционирования любого из агрегатов и системы в целом.Имитационные модели воспроизводят процесс функционирования и параметры исследуемых систем, отталкиваясь от известных свойств их элементов – с помощью объединения моделей элементов в структуру, соответствующую изучаемой системе, и имитации функционирования элементов в их взаимодействии. Исследование систем с помощью имитационных моделей выполняется в несколько этапов: установление принципов построения модели. Задача данного этапа – выработать главную цель модели (набор характеристик и параметров, область определения, требования к точности результатов и т. д.). При этом выдвигаются предположения о параметрах моделируемой системы, принимаются допущения для использования необходимых математических методов и конкретизируются эксперименты, которые будут проводиться на модели; разработка модели. На данном этапе выполняется разработка программы моделирования. При этом общий замысел модели преобразуется в конкретное алгоритмическое описание. Этап завершается проверкой адекватности модели и её работоспособности; моделирование на ЭВМ. Задача этого этапа состоит в получении данных о поведении изучаемой системы и их обработке, а при проектировании – в выборе параметров, оптимизирующих отдельные характеристики системы и соответствующих заданным ограничениям. Самое важное свойство имитационной модели – универсальность, которая обусловливается следующими параметрами: возможность изучения систем любой сложности. Повышение сложности системы приводит к увеличению объема данных, обрабатываемых моделью, и времени, затрачиваемого на моделирование, но при этом не меняется сам принцип её построения; отсутствие ограничений уровня детализации. С использованием алгоритмов можно воспроизвести любые взаимосвязи между элементами системы и процессы их работы. Детализация оказывает влияние лишь на объем соответствующей программы и количество времени, затрачиваемого на моделирование системы. Особенности организации и функционирования, мешающие применению аналитических моделей, без труда воссоздаются при имитации; модель является источником информации о поведении изучаемой системы – эксперименты на модели позволяют приобретать дополнительную информацию о ней. При этом имитационные модели обладают и рядом недостатков: на создание имитационной модели могут уходить значительно большие временные затраты; поскольку полученное решение основано на конкретных заданных алгоритмах функционирования, фиксированных параметрах и частях системы, то оно всегда будет носить только частный характер. Не смотря на эти недостатки, имитационные модели являются одними из наиболее обширно применяемых методов при решении задач проектирования и анализа сложных процессов и систем, а также при исследовании особенностей их работы. Таким образом, наибольшее распространение получили экспериментальные и модельные методы исследования вычислительных систем. Экспериментальные методы исследования вычислительных систем помогают получить наиболее достоверные сведения об объекте, но при этом имеют большую трудоёмкость и время, затрачиваемые на эксперименты, а также их результаты зависят от конфигурации системы и режимов её работы. Модельные методы, в свою очередь, делятся на аналитические и имитационные. Первые просты в реализации, но характеризуются значительными погрешностями. Имитационные методы позволяют описать поведение объекта с использованием алгоритмической модели. Главное преимущество этих методов – универсальность. Они позволяют исследовать объекты любой сложности и с любым уровнем детализации. Имитационные модели используются для изучения сложных систем. 1.4 Выводы В современных микропроцессорах широко используется конвейерная обработка. Для повышения их производительности применяют мульти- и суперконвейеризацию. Эффективная работа конвейера может быть нарушена из-за конфликтов. Стремление максимально повысить производительность процессора привело к использованию двух разных подходов к устранению конфликтов. Первый реализуется динамически, в процессе выполнения программы. Он характерен для суперскалярных процессоров. Устранение большинства конфликтов с помощью компилятора характерно для VLIW – процессоров. Наконец, процессоры EPIC используют сочетание обоих подходов. Несмотря на целый ряд недостатков, суперскалярные процессоры занимают лидирующее положение на рынке. Их важнейшим достоинством является независимость исполняемого кода программы от внутренней структуры процессора. Это позволяет выполнять одну и ту же программу на любой модели микропроцессора. При исследовании вычислительных систем решаются задачи анализа, развития и проектирования. Для этого используются модели вычислительных процессов и системы в целом, которые позволяют определить их характеристики. Наибольшее распространение получили экспериментальные и модельные методы исследования вычислительных систем. Экспериментальные методы исследования вычислительных систем помогают получить наиболее достоверные сведения об объекте, но при этом имеют большую трудоёмкость и время, затрачиваемые на эксперименты, а также их результаты зависят от конфигурации системы и режимов её работы. Модельные методы, в свою очередь, делятся на аналитические и имитационные. Первые просты в реализации, но характеризуются значительными погрешностями. Имитационные методы позволяют описать поведение объекта с использованием алгоритмической модели. Главное преимущество этих методов – универсальность. Они позволяют исследовать объекты любой сложности и с любым уровнем детализации. Имитационные модели используются для изучения сложных систем. 1 2 |
