СОЗДАНИЕ КОНТЕКСТНЫХ ЗАДАЧ В ПРОЦЕССЕ ОБУЧЕНИЯ ШКОЛЬНИКОВ МАТЕМАТИКЕ. Евелина, Седова_статья. Создание контекстных задач в процессе обучения школьников математике
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
СОЗДАНИЕ КОНТЕКСТНЫХ ЗАДАЧ В ПРОЦЕССЕ ОБУЧЕНИЯ ШКОЛЬНИКОВ МАТЕМАТИКЕ Евелина Л.Н. Доцент кафедры физики, математики и методики обучения, к.п.н., доцент, Самарский государственный социально-гуманитарный университет, Седова К.П. Студент 5 курса факультета математики, физики и информатики Самарского государственного социально-педагогического университета Аннотация. Гуманизация образования, как средство нравственного воспитания молодого поколения, занимает центральное место в решении проблемы развития общества. Одним из каналов реализации гуманистического подхода в обучении стала теория личностно – ориентированного обучения. По мнению авторов статьи, эффективным направлением реализации личностно-ориентированного подхода в образования на данный момент является контекстный подход к отбору содержания и форм организации учебно-познавательной деятельности обучающихся. Ключевые слова: личностно-ориентированное обучение, контекстный подход в обучении, контекстная задача. Согласно теории личностно-ориентированного обучения, образовательный вектор направлен на развитие личности учащегося, обладающего способностями воспроизводить содержание, путь и методы познания, проявляя собственную активность [4, с.26]. Организация процесса взаимодействия учителя и учащегося позволяет ребенку самостоятельно выделять существенные свойства объектов, определять их структуру, связи между несколькими объектами. В свою очередь, традиционное обучение отвергает субъективный опыт, считая его несущественным и несовершенным. Реализация личностно – ориентированного обучения возможна через использование контекстного подхода в обучении. На сегодняшний день понятием «контекста» активно оперируют исследователи гуманитарной области (педагоги, лингвисты, политологи). Под «контекстом» подразумевается процесс семантизации психических содержаний за счет соотнесения объекта с некоторым окружением. В результате в восьмидесятые годы XX столетия формируется контекстный подход в форме теории и методики контекстного обучения в образовании, а в начале нашего столетия – психологической методики научного исследования. Абстрагируясь от системы контекстного подхода, можно найти научные обоснования создания и внедрения контекстных учебников. Изучением данного вопроса в девяностые годы XX столетия занимались некоторые ученые, в частности, В.Д. Еремеева, Б.Л. Ливер, Т.П. Хризман. Используя методы нейропсихологии, они смогли сделать вывод о «контекстно – зависимых детях» - детях, которым особенно трудно воспринимать и усваивать материал вне контекстов (дети с развитым правым полушарием), однако большая часть учебной литературы контекстом не снабжена. Работая по данному вопросу, Э.Г. Гельфман и М.А. Холодная [1] выдвинули ряд требований для контекстов, используемых в учебных текстах. Был выдвинут принцип «текста в контексте». Примером может послужить изложение некоторого математического знания в рамках нематематического контекста, при этом используются игровые ситуации, исторические сведения, диалоги и размышления ученых, афоризмы. Предлагаемая избыточность контекста, по мнению М.А. Холодной, позволяет обучающемуся осваивать предметные понятия и явления в более обширных межпредметных связях, создавая при этом широкое смысловое пространство. Можно сделать вывод, что в своем большинстве контекстный подход ориентируется на личностно – смысловой, а уже потом на когнитивный аспект феномена контекста. Сформирован ряд требований, предъявляемых к задаче, которая претендует на роль контекстной: 1) задача основывается на реальном жизненном опыте учащихся, знаниях, взглядах, мнениях; 2) задача представляется в нестандартной/оригинальной форме, что способствует повышению интереса у учащихся; 3) в описании задачи содержатся математические и нематематические элементы и их взаимосвязь; 4) задача соответствует образовательной программе; 5) контекст задачи представляется в разных формах кодировки: от «сухого» текста до графиков и таблиц; 6) математическая модель задачи соответствует уровню подготовленности учащихся; 7) развитие сюжета; 8) задача в скрытом виде включает в себя основную идею занятия. Проанализируем учебно–методическую литературу на предмет наличия контекстных задач на примере учебника Математика: 5 класс: учебник для учащихся общеобразовательных учреждений /А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М: Вентана – Граф, 2013. 304с. Наиболее подходящей, на наш взгляд, под понятие контекстной, является задача №112 [3, с.35] (рисунок 1). 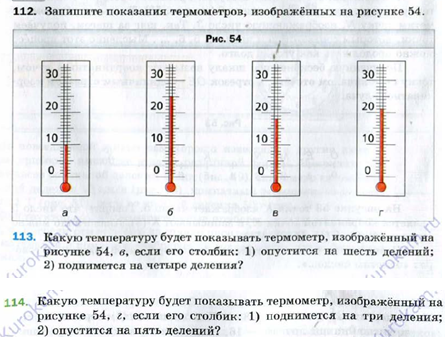 Рисунок 1. Задачи №112-114 Проверим, удовлетворяет ли она всем требованиям контекстной задачи: 1) задача опирается на реальный жизненный опыт учащихся; 2) задача нестандартна для восприятия, способствует повышению интереса; 3) в задаче отражены математические и нематематические проблемы и их взаимосвязь; 4) задача соответствует программе курса; 5) контекст задачи представлен в форме рисунка; 6) описанная математическая модель соответствует уровню подготовленности школьников; 7) сюжет задачи считается частично последовательным, так как сюжет развивается только от задания 112 к заданию 113, а задание 114, относящееся к тому же контексту, является аналогичным 113. 8) задача является «ловушкой» частично, так как пример шкалы термометра был использован в теоретическом описании параграфа. Таким образом, задача может быть заявлена как контекстная, но с частичным выполнением требований. Представленный перечень, включающий не более 15 задач (при общем количестве задач в учебнике 1222) является единственным списком задач, которые можно считать контекстными, в данном пособии. Несмотря на то, что достаточно большое количество задач разработчиками помещено в контексты, задачи не удовлетворяют основным требованиям контекстных задач. Распространенными неточностями, которые наблюдаются в данных задачах, являются отсутствие развития контекста (№137, №165, №201, №202, №234, №319, №336 №541) и однообразное представление информации. Задачи ограничиваются одним вопросом к тексту, а если перед учащимся ставится несколько вопросов, то, зачастую, они аналогичные. Также можно обнаружить задачи с некорректным контекстом. Примером служит задание №814 [3, с.210] (рисунок 2). Человек в повседневной жизни не оперирует деньгами в виде обыкновенных дробей. Таким образом, задача теряет контекстную ценность. 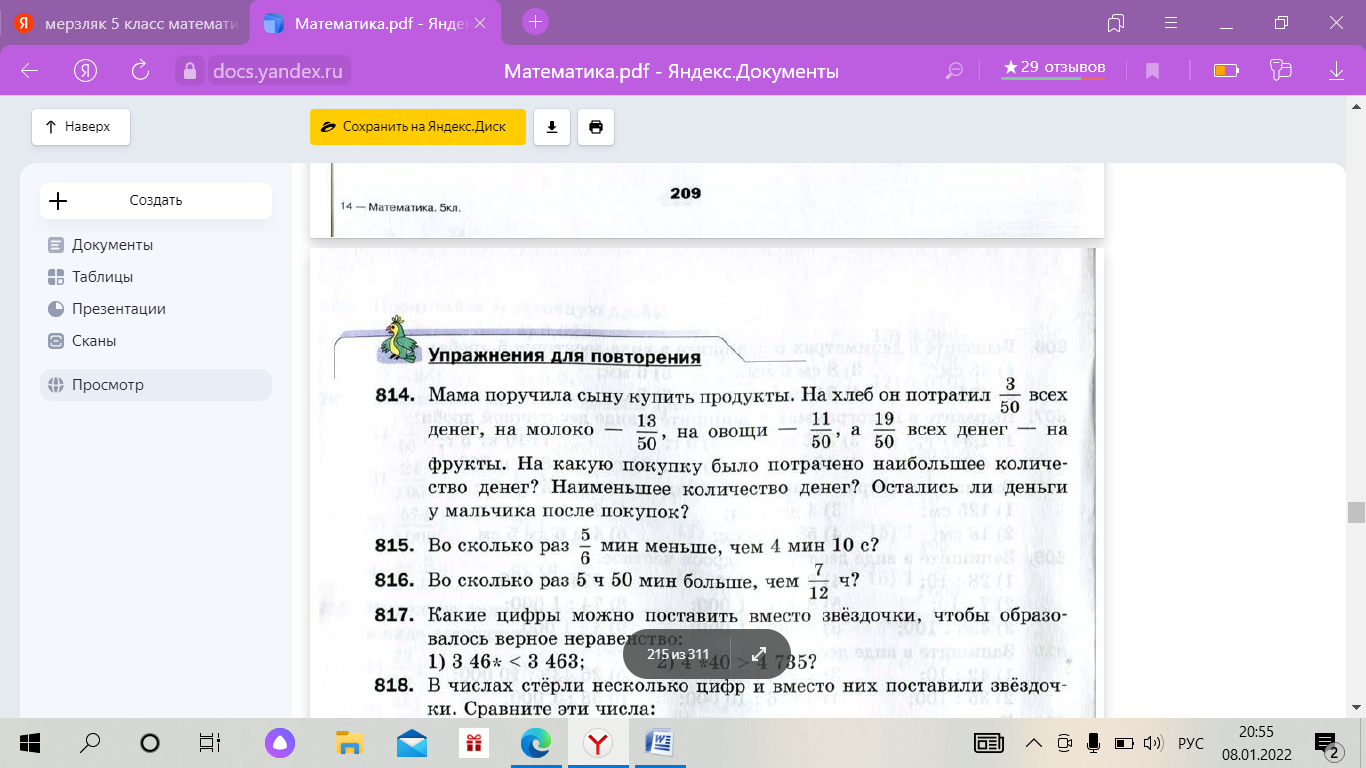 Рисунок 2. Задача №814 Составим контекстную задачу на тему «Десятичные дроби» по выше описанным правилам и требованиям. Задача. В южной части Восточной Сибири расположилось самое глубокое озеро нашей планеты – Байкал. Оно образовалось в результате тектонического движения литосферных плит. На сегодняшний день Байкал является крупнейшим по площади пресноводным озером. Максимальная глубина озера составляет 1642 метра, а его средняя глубина 758 метров. Задание 1. Для исследования озерного дна ученым необходимо знать коэффициент емкости озера (отношение средней глубины озера к его максимальной глубине). Этот коэффициент помогает определить форму чаши озера. Определите коэффициент емкости озера Байкал и результат округлите до десятых. Задание 2. Для заполнения чаши озера Байкал всем рекам мира необходимо 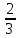 года отдавать свои воды озеру. Сколько это месяцев? года отдавать свои воды озеру. Сколько это месяцев?Задание 3. На фотографии (рисунок 3) представлен вид озера Байкал из космоса. Посчитайте примерную площадь озера, учитывая, что площадь одной клетки равна 5287 км2. 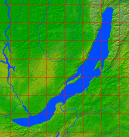 Рисунок 3. Вид озера Байкал Данная задача несет в себе такие контексты, как пространственно- временной (при вычислении коэффициента емкости озера), контекст межпредметности (использование математического знания в области географии и морфометрии озер), контекст профессиональной деятельности, а также удовлетворяет всем требованиям, предъявляемым к контекстным задачам. Количество контекстных задач к каждому разделу учебной программы должно быть не менее трех. Задачи, предлагаемые разработчиками PISA, как правило, охватывают несколько разделов, а задачи, представленные в учебной литературе, не всегда удовлетворяют требованиям контекстных задач. Поэтому вопросы методики создания контекстных задач выступают на передний план, несмотря на массовую актуализацию данной темы. Список литературы 1. Гельфман Э.Г., Холодная М.А. Психодидактика школьного учебника. Интеллектуальное воспитание учащихся. – СПб.: Питер, 2006. 384 с. 2. Егупова М.В. Практико-ориентированное обучение математике в школе как предмет методической подготовки учителя. Монография. – М.: МПГУ, 2014. 284 с. 3. Мерзляк А.Г. Математика: 5 класс: учебник для учащихся общеобразовательных учреждений /А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М: Вентана – Граф, 2013. 304 с. 4. Пинская М.А., Михайлова А.М. Компетенции «4К»: формирование и оценка на уроке: Практические рекомендации. - М.: корпорация «Российский учебник», 2019. 76с. |
