5 кл преемственность. Специальные математические знания, умения и навыки
 Скачать 276.05 Kb. Скачать 276.05 Kb.
|
|
Переход из начальной в среднее звено школы традиционно считается одной из наиболее педагогически сложных школьных проблем, а период адаптации в 5-м классе – одним из труднейших периодов. Проблема преемственности в обучении математике приобрела особое значение в связи с широким внедрением Федерального государственного образовательного стандарта. ФГОС, в том числе, направлен на обеспечение преемственности основных образовательных программ начального общего, среднего (полного) общего, профессионального образования. Цели обучения и подход к обучению имеют большие различия. В качестве главного результата образования в соответствии с ФГОС рассматривается не система знаний, умений и навыков сама по себе, а набор ключевых компетентностей в интеллектуальной, гражданско-правовой, коммуникационной, и информационной сферах. Проблемы преемственности в преподавании математики между начальной школой и 5 классом можно поделить на три группы: организационно-психологические; общеучебные умения и навыки; специальные математические знания, умения и навыки. Специальные математические знания, умения и навыки. 1. Недостаточные умения устных вычислений (все арифметические действия в пределах до ста учащиеся должны выполнять устно). Возможности разрешения: постоянное подкрепление знаний таблиц сложения и умножения, систематическое проведение содержательного и напряженного устного счета. 2. Ошибки в письменном делении многозначных чисел и письменном умножении многозначных чисел. Возможности разрешения: регулярное повторение всех этапов алгоритма выполнения деления и умножения, систематическое включение в устную работу заданий на табличное умножение и деление, сложение и вычитание. 3. Слабое знание правил порядка действий (в том числе и в выражениях со скобками). Возможности разрешения: после записи вычислительных примеров начинать с выделения отдельных «блоков», из которых он состоит, обращать внимание на «сильные» и «слабые» знаки арифметических действий, а затем расставлять номера действий. 4. Недостаточные умения решать текстовые задачи (даже в одно - два действия). Возможности разрешения: предлагать сначала представить себе ситуацию, о которой идет речь в задаче, изобразить её на рисунке или схеме; при обсуждении решения – вопросы: как догадались, что первое действие именно такое? 5. Недостаточное развитие графических умений. Возможности разрешения: регулярное выполнение чертежей как на бумаге в клетку, так и на нелинованной бумаге, построение фигур по командам. 6. Формальные представления об уравнении, его корне, способах проверки правильности решения уравнения. Возможности разрешения: большее внимание уделять первым этапам формирования понятия переменной, верного и неверного равенства, нахождение значения выражения с переменной. 7. Недостаточно грамотная математическая речь учащихся. Возможности разрешения: учителю чаще давать образцы чтения выражений, равенств, уравнений и неравенств, склонять числительные, тренировать школьников в верном чтении математических выражений, использовании названий натуральных чисел и дробей в косвенных падежах. Как показывает практика, в первые месяцы 5-го класса многие ученики не справляются с поставленными перед ними вопросами и заданиями. В это период у детей наблюдается повышенная возбудимость, быстрая утомляемость, рассеянное внимание, и как следствие, снижение качества успеваемости. И в этом случае на помощь приходит занимательная математика, истории развития математики. Я на каждом уроке во время физ. минутки, стараюсь давать задачи – шутки, задачи на логику. Например: Двое подошли к реке. У берега стояла лодка, которая может вместить лишь одного человека, но они оба переправились. Как это могло случиться? (Стояли на разных берегах реки). Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода? (Нет, 72 = 3 суток, будет ночь). Горело 7 свечей. 2 свечи погасили, а остальные продолжали гореть. Сколько свечей осталось? (2, остальные сгорели). В корзине три яблока. Как поделить их между тремя детьми так, чтобы одно яблоко осталось в корзине? (Отдать одно яблоко вместе с корзиной). На берёзе три толстых ветки, на каждой толстой ветке по три тоненьких веточки. На каждой тоненькой веточке по одному яблочку. Сколько всего яблок? (Нисколько – на берёзе яблоки не растут.) и т.д. Особая роль в 5 классе отводится отработке вычислительных навыков. В устных вычислениях развивается память, внимание, сосредоточенность – важные элементы общего развития ребенка. Много времени на уроке отвожу игровым элементам на логическое мышление, например: Устный счет (числа записаны вразброс, найти и показать их от 1 до 90). 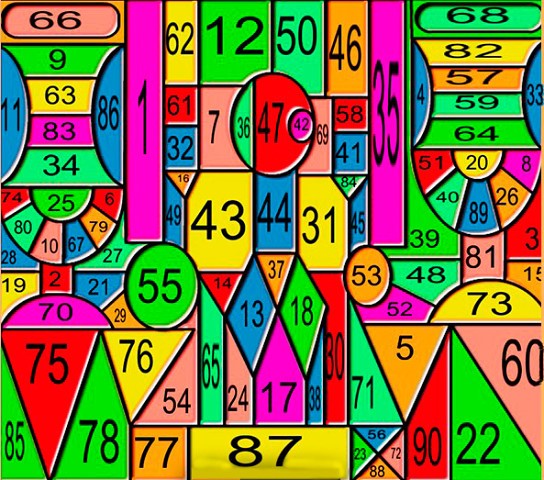 Из фигур: круг, треугольник, квадрат нарисовать человека. Сколько лет человечку? (Сложи все найденные цифры).  Найти сколько животных изображено на рисунке?  Внимательно посмотрите на квадрат, в клетках которого, нарисованы фигуры. Сложите по памяти такую же таблицу. 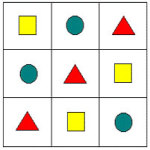 Все эти задания позволяют за короткое время сконцентрировать внимание ребят, развивают память, логику, скорость мышления, наблюдательность и т.п. Очень важно в короткие сроки помочь пятикласснику адаптироваться в новых, необычных для него условиях и для этого преподавателю нужно вести работу с учетом тех знаний, которые они получили, и использовать те методические приемы, которые характерны для начальной школы. Например, это: Подробное разъяснение домашнего задания Ежедневный контроль за выполнением классного и домашнего заданий Частое оценивание знаний учащихся формирует чувство ответственности к учебе, поэтому нужно проводить тренировочные, развивающие контролирующие самостоятельные работы и тестовые задания Особое место уделять развитию речи на уроках математики, пополнение словарного запаса новыми терминами через формулировку правил, определений, работа с учебником, умению пересказывать, выделяя главную мысль. Формирование новых знаний с опорой на знакомый учащимся материал знаний, с использованием знакомых оборотов речи, дает хороший результат продвижения по уровню успеваемости. В качестве рекомендации хотелось бы пожелать, чтоб учителя начальных классов учитывали значимость вычислительных навыков, без которых обучение в старших классах становится проблематичным (таблица умножения должна быть отработана до автоматизма), желательно отработать и приемы вычисления на 11, 5, 25, 125, например, 4 * 25, 8* 125, 11*31 и т.п. Учащиеся к 5 классу должны уметь самостоятельно добывать знания. Увеличение нагрузки в 5-х классах ведет к переутомлению, поэтому на уроках обязательно введение физкультминуток, физ. пауз, аутотренингов. На учителя ложится такая нагрузка, когда он должен постоянно увлекать за собой детей в работе, быть справедливым, не терять чувство юмора. |
