Спектральний аналіз періодичних та неперіодичних детермінованих безперервних сигналів. Николаенко ТЗ-18 Курсовая. Спектральний аналіз періодичних та неперіодичних детермінованих
 Скачать 1.91 Mb. Скачать 1.91 Mb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДНІПРОВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ФІЗИКО-ТЕХНІЧНИЙ ФАКУЛЬТЕТ КАФЕДРА РАДІОЕЛЕКТРОННОЇ АВТОМАТИКИ КУРСОВА РОБОТА З дисципліни «Радіотехнічні кола та сигнали» НА ТЕМУ: Спектральний аналіз періодичних та неперіодичних детермінованих безперервних сигналів Виконавець: Студент групи ТЗ-18-1 Ніколаєнко С.В. Комісія з прийому курсової роботи: Петренко О.М. Мазуренко В.Б. Селіванов Ю.М. Дніпро 2019 Завдання №1 Отримати представлення сигналу у вигляді ряду Фур'є (в синусно-косинусній формі, дійсній формі та в комплексної формі) з розрахунком перших десяти членів ряду (частоти, амплітуди і фази перших десяти гармонік) для кожного з вказаних сигналів. Для кожного з сигналів: Представити графік зміни сигналу за часом. Представити амплітудну та фазову спектральні діаграми (число гармонік не менше 10-ти).
Завдання №2 Записати в аналітичному вигляді спектральну функцію для заданого відеоімпульсу, побудувати і представити у вигляді графіків амплітудний і фазовий спектри сигналу. Записати в аналітичному вигляді спектральну функцію для заданого радіоімпульсу, побудувати і представити у вигляді графіку (для позитивних частот) амплітудний спектр сигналу.
Завдання №1 1. Прямокутний сигнал. Вхідні параметри: f= 0,5 Гц; А1 = 30 В; q = 5; n = 10; 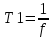 ; ; 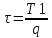 ; ω = 2πf;ω = 3.14 Гц; τ = 0.5 c; ; ω = 2πf;ω = 3.14 Гц; τ = 0.5 c;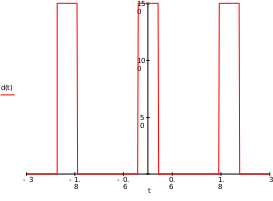 Рис.1 Графік прямокутного сигналу d(t) 2Фур'є будуть присутні лише косинусні складові аk, bk = 0; Розрахуємо перші десять коефіцієнтів ak і bk по формулам: 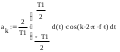 , де k = 0 .. 10; , де k = 0 .. 10; 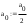 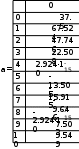 Запишемо представлення ряду Фур’є в синусно-косинусній формі: 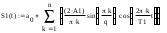 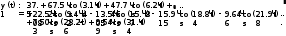 Розрахуємо перші десять коефіцієнтів Ak і φk по формулам: 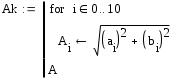 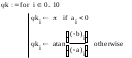  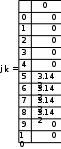 Запишемо представлення ряду Фур’є в дійсній формі: 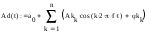 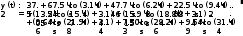 Побудуємо амплітудну і фазову спектральні діаграми сигналу: 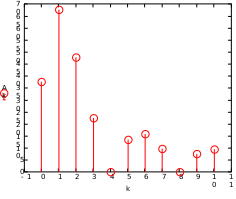 Рис.2 Амплітудна спектральна діаграма  Рис.3 Фазова спектральна діаграма Розрахуємо перші десять коефіцієнтів Сk по формулі: 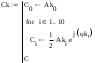 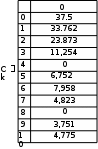 Запишемо представлення ряду Фур’є в комплексній формі: 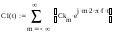 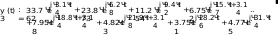 2. Пилкоподібний сигнал. Вхідні параметри: f=1500 Гц; А1 = 150 В; n = 10; 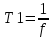 ; ; 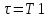 ; ω = 2πf;ω = 9.42*103 Гц; τ = 6.667*10-4 c; ; ω = 2πf;ω = 9.42*103 Гц; τ = 6.667*10-4 c;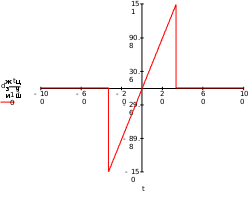 Рис.4 Графік пилкоподібного сигналу d(t/105) Даний сигнал є непарною функцією, тому в синусно-косинусній формі ряду Фур'є будуть присутні лише синусні складові bk, аk = 0; Розрахуємо перші десять коефіцієнтів ak і bk по формулам: 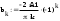 , де k = 0 .. 10; , де k = 0 .. 10;  Запишемо представлення ряду Фур’є в синусно-косинусній формі: 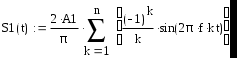 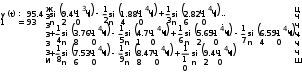 Розрахуємо перші десять коефіцієнтів Ak і φk по формулам: 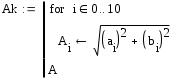 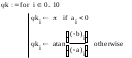 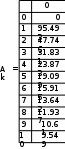  Запишемо представлення ряду Фур’є в дійсній формі: 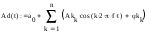 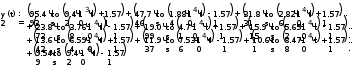 Побудуємо амплітудну і фазову спектральні діаграми сигналу: 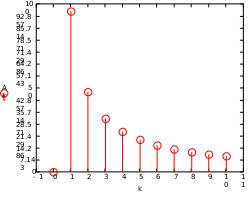 Рис.5 Амплітудна спектральна діаграма 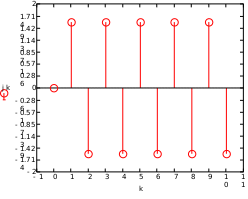 Рис.6 Фазова спектральна діаграма Розрахуємо перші десять коефіцієнтів Сk по формулі: 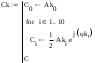 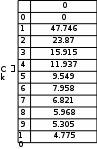 Запишемо представлення ряду Фур’є в комплексній формі: 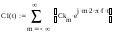 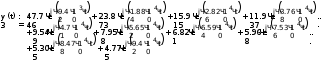 3. Трикутний сигнал. Вхідні параметри: f= 3500 Гц; А1 = 150 В; n = 10; 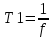 ; ; 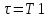 ; ω = 2πf;ω = 2.199*104 Гц; τ = 2.857*10-4 c; ; ω = 2πf;ω = 2.199*104 Гц; τ = 2.857*10-4 c;. 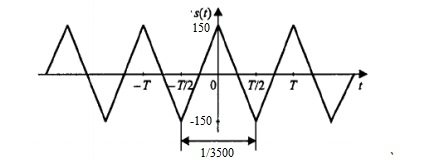 Рис.7 Графік трикутного сигналу d(t) Даний сигнал є парною функцією, тому в синусно-косинусній формі ряду Фур'є будуть присутні лише косинусні складові аk, bk = 0; Розрахуємо перші десять коефіцієнтів ak і bk по формулам: 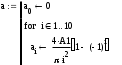 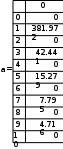 Запишемо представлення ряду Фур’є в синусно-косинусній формі: 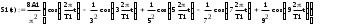 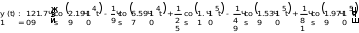 Розрахуємо перші десять коефіцієнтів Ak і φk по формулам: 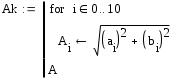 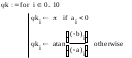 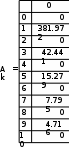  Запишемо представлення ряду Фур’є в дійсній формі: 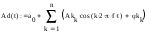 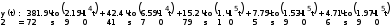 Побудуємо амплітудну і фазову спектральні діаграми сигналу:  Рис.8 Амплітудна спектральна діаграма 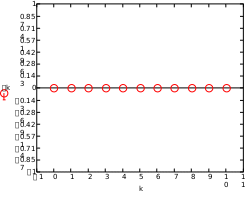 Рис.9 Фазова спектральна діаграма Розрахуємо перші десять коефіцієнтів Сk по формулі: 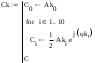 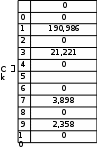 Запишемо представлення ряду Фур’є в комплексній формі: 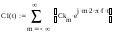 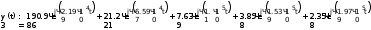 4. Меандр. Вхідні параметри: f= 350 Гц; А1 = 150 В; q = 2; n = 10; 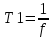 ; ; 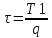 ; ω = 2πf;ω = 2,198 *103 Гц; τ = 1,429*10-3 c; ; ω = 2πf;ω = 2,198 *103 Гц; τ = 1,429*10-3 c;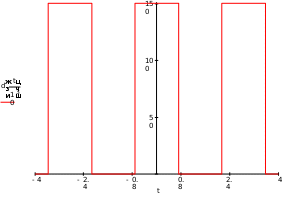 Рис.10 Графік меандру d(t/103) Даний сигнал є парною функцією, тому в синусно-косинусній формі ряду Фур'є будуть присутні лише косинусні складові аk, bk = 0; Розрахуємо перші десять коефіцієнтів ak і bk по формулам: 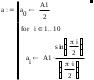 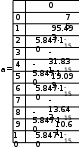 Запишемо представлення ряду Фур’є в синусно-косинусній формі: 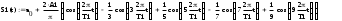 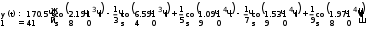 Розрахуємо перші десять коефіцієнтів Ak і φk по формулам: 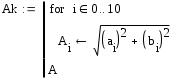 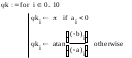  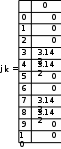 Запишемо представлення ряду Фур’є в дійсній формі: 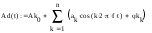 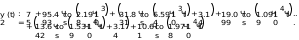 Побудуємо амплітудну і фазову спектральні діаграми сигналу: 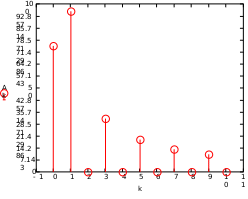 Рис.11 Амплітудна спектральна діаграма  Рис.12 Фазова спектральна діаграма Розрахуємо перші десять коефіцієнтів Сk по формулі: 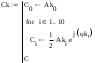 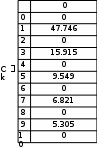 Запишемо представлення ряду Фур’є в комплексній формі: 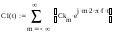 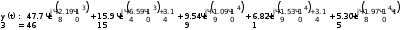 Завдання №2 1. Прямокутний сигнал Вхідні параметри: f0= 106 Гц; А1 = 150 В; τ = 4*10-5 c; 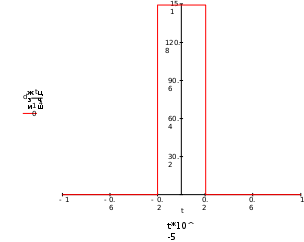 Рис. 13 Графік прямокутного сигналу d(t/105) Спектральна функція прямокутного імпульсу 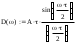 Представимо у вигляді графіків амплітудний і фазовий спектри сигналу 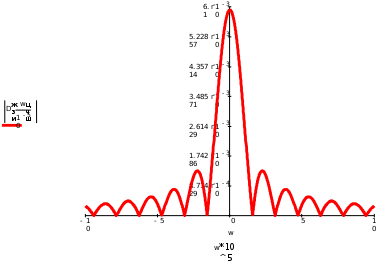 Рис.13 Амплітудний спектр прямокутного сигналу 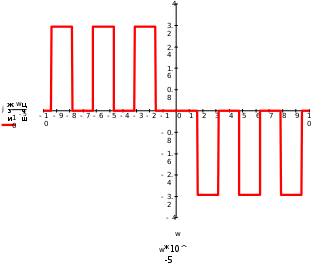 Рис.14 Фазовий спектр прямокутного сигналу Помножимо сигнал d(t) на гармонійну функцію g(t) = cos(ω0t+φ0) 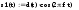 Знайдемо спектральну функцію S1(ω) нового сигналу s1(t) 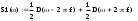 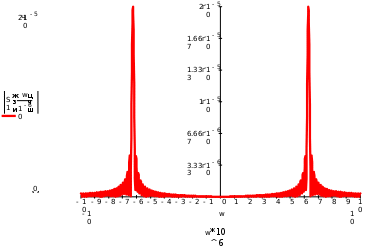 Рис.15 Амплітудний спектр прямокутного радіоімпульсу 2. Трикутний сигнал Вхідні параметри: f0= 106 Гц; А1 = 150 В; τ = 4*10-5 c; 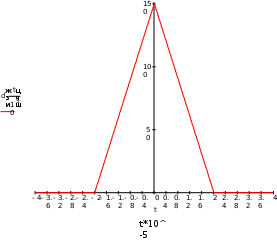 Рис. 16 Графік трикутного сигналу d(t/105) Спектральна функція трикутного імпульсу 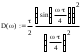 Представимо у вигляді графіків амплітудний і фазовий спектри сигналу 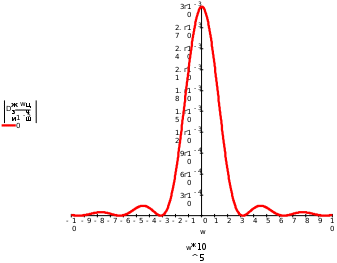 Рис.17 Амплітудний спектр прямокутного сигналу 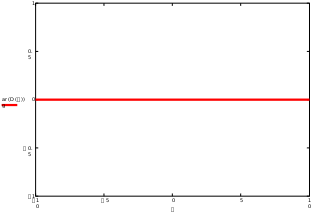 Рис.18 Фазовий спектр прямокутного сигналу Помножимо сигнал d(t) на гармонійну функцію g(t) = cos(ω0t+φ0) 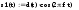 Знайдемо спектральну функцію S1(ω) нового сигналу s1(t) 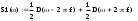 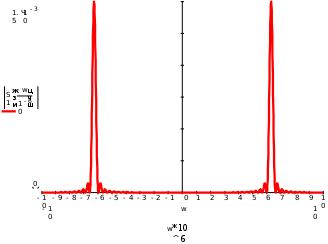 Рис.19 Амплітудний спектр трикутного радіоімпульсу 3. Двосторонній експоненційний сигнал Вхідні параметри: f0= 106 Гц; А1 = 150 В; а = 1.2*106 1/c; 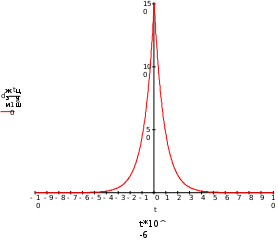 Рис. 13 Графік двостороннього експоненційного сигналу d(t/106) Спектральна функція двостороннього експоненційного імпульсу 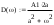 Представимо у вигляді графіків амплітудний і фазовий спектри сигналу 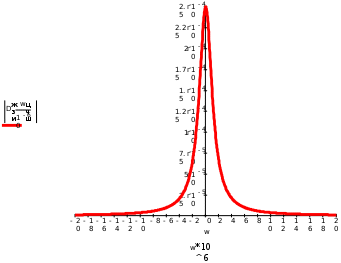 Рис.13 Амплітудний спектр двостороннього експоненційного сигналу 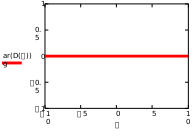 Рис.14 Фазовий спектр двостороннього експоненційного сигналу Помножимо сигнал d(t) на гармонійну функцію g(t) = cos(ω0t+φ0) 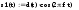 Знайдемо спектральну функцію S1(ω) нового сигналу s1(t) 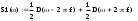 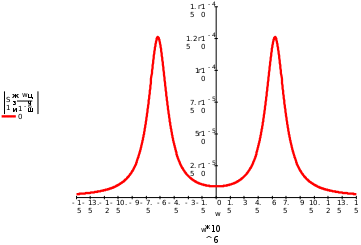 Рис.15 Амплітудний двостороннього експоненційного сигналу | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
