инж график. Способ сфер
 Скачать 62.73 Kb. Скачать 62.73 Kb.
|
|
Министерство образования Московской области Государственное бюджетное профессиональное образовательное учреждение Московской области «Электростальский колледж» Инженерная графика Тема: «Способ сфер». Выполнил студент: 2 курса, группы ПБ 20-01, Прокопов Виктор Алексеевич; Электросталь 2022 г. Способ концентрических сфер Этот способ применяется в случае, когда оси двух поверхностей вращения пересекаются под некоторым углом и находятся в плоскости, параллельной какой-либо плоскости проекций (особенно в том случае, когда на чертеже дана только одна проекция деталей). Шар со всякой поверхностью вращения, ось которой проходит через центр шара, пересекается по окружностям. Эти окружности находятся в плоскостях, перпендикулярных к оси поверхности вращения, и проецируются на одну из плоскостей проекций в виде прямых, в этом состоит преимущество способа сфер. На рисунке дана фронтальная проекция шара, пересекающегося с конусом и цилиндром. Как видно, центр шара находится на пересечении осей данных поверхностей, а линии его пересечения с ними — окружности диаметров: 1-2, 3-4, 5-6. 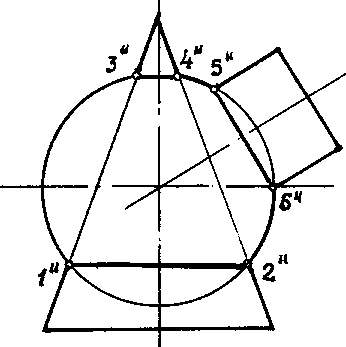 Пример. Даны конус и цилиндр, оси которых пересекаются под некоторым углом. Построить линию пересечения заданных поверхностей. Наивысшую и наинизшую точки 1 и 2 линии пересечения находят непосредственно в пересечении крайних образующих на фронтальной проекции заданных поверхностей. 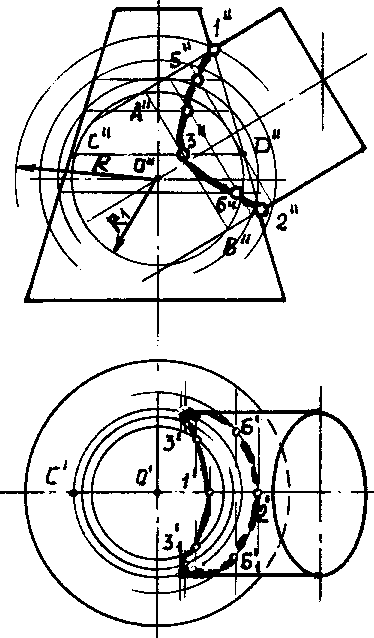 Для нахождения промежуточных точек 3, 4, 5, ... проводят из центра О” ряд вспомогательных концентрических сфер радиуса от RдоR1, которые рассекают заданные тела по окружностям. На фронтальной проекции эти окружности проецируются в прямые линии и, пересекаясь между собой, определяют точки линии перехода. Так, для нахождения точек 3 (одна из них невидима) проводят сферу радиуса R1, которая пересечет цилиндр по окружности диаметра а” b”, конус — по окружности диаметра c”. В пересечении указанных окружностей определяются точки 3. Горизонтальные проекции этих точек находятся на окружности (параллели), проведенной из центра О' радиусом, равным c ” d”/2. Все остальные промежуточные точки определяются аналогично. Так как пересекающиеся тела симметричны, их линия пересечения также симметрична. На фронтальной проекции невидимая часть линии пересечения сливается с видимой. Точки 4 (на горизонтальной проекции) служат границами раздела видимой и невидимой части линии пересечения. Найденные точки соединяют плавной кривой по лекалу. Способ эксцентрических сфер Указанный способ построения линии пересечения двух поверхностей состоит в применении вспомогательных сфер, имеющих различные центры.  В этом примере центры вспомогательных сфер можно брать в любой точке оси поверхности вращения. Поэтому построение линии пересечения в этом случае можно выполнить не только способом концентрических сфер, но и способом эксцентрических сфер. В примере проведены четыре сферы радиусов r1, r2, r3, r4 из различных центров О1, О2, О3, О4, расположенных на оси i поверхности вращения. Каждая из этих сфер пересекается с данными поверхностями по окружностям, точки пересечения которых и будут точками линии пересечения поверхностей. Даны усеченный конус и четверть кольца, оси которых пересекаются под углом 90о. Построить линию пересечения заданных поверхностей. Наивысшую и наинизшую точки 1 и 2 линии пересечения заданных поверхностей находят непосредственно в пересечении крайних образующих на фронтальной проекции. Для нахождения промежуточных точек 3 через центр кругового кольца проводят фронтально-проецирующую плоскость Р. Она пересечет кольцо по окружности; a”— ее фронтальная проекция, которая находится на сфере, проведенной из центра О1. Проекцию О1 центра сферы находят на пересечении оси конуса и касательной t” О1 к направляющей окружности кольца в точке t”. Сфера с центом в точке О1 пересекает конус по окружности d”. 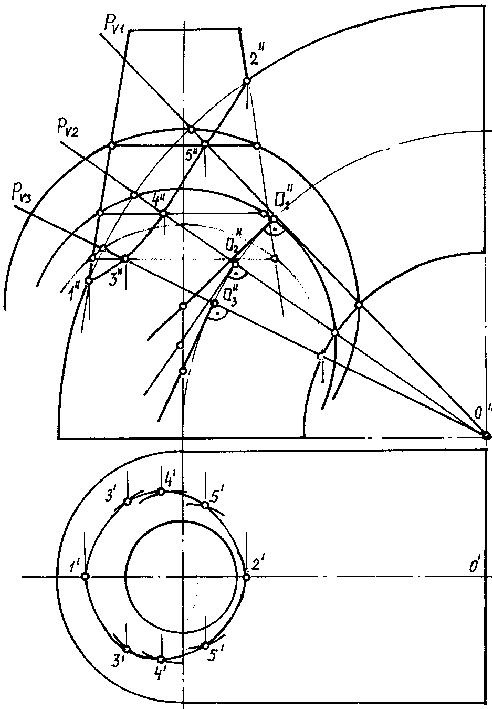 В пересечении a” и c” получают две общие точки 3 и 31 линии пересечения. Промежуточные точки 4 и 5 определяют аналогично. Горизонтальные проекции точек 3, 4, 5 линии пересечения определяют при помощи фронтальной плоскости Q. Эта плоскость рассекает кольцо по параллели, что видно из чертежа. Точки 4 лежат на крайних образующих горизонтальной проекции конуса и служат границами раздела между видимой и невидимой частями линии пересечения. Найденные точки соединяют плавной кривой по лекалу. +Часто этот способ называют способом скользящего шара. |
