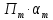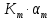КР_Трофимова. Спрос на продукцию компании задается функцией Qx 12000 3Px 4Py 1M 2Ax
 Скачать 137.12 Kb. Скачать 137.12 Kb.
|
|
Задание 1 Спрос на продукцию компании задается функцией Qx = 12000 – 3Px + 4Py – 1M + 2Ax; где Ax – затраты на рекламу товара Х, 2000 долл.; Px − цена единицы товара Х, 200 долл.; Pу − цена единицы товара У, 15 долл.; М – потребительский доход, 10000 долл. а. Какое количество товара Х купят потребители? Qx = 12000 – 3Px + 4Py – 1M + 2Ax=12000 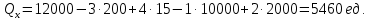 б. Являются ли Х и У взаимодополняющими или взаимозаменяющими товарами? 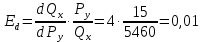 Так как 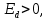 то товары взаимозаменяемые. то товары взаимозаменяемые.в. Является ли Х нормальным или низшим товаром? 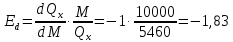 Так как 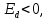 товар низший. товар низший.г. Определите уравнение кривой спроса и обратной кривой спроса. 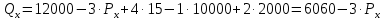 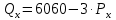 – уравнение кривой – уравнение кривой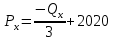 – уравнение обратной кривой спроса – уравнение обратной кривой спроса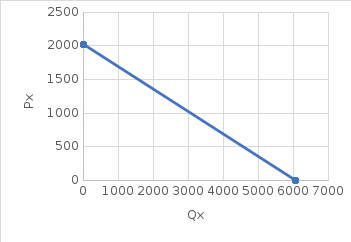 Задание 2. а. Предположим, что вводится К единиц капитала = 3; составьте таблицу, содержащую значения общего выпуска продукции, среднего продукта, предельного продукта при вводимом факторе – труде, меняющемся от 1 до 8 единиц труда.
б. Используя указанные данные, постройте график с кривыми общего выпуска продукции, среднего продукта и предельного продукта. Укажите на графике: 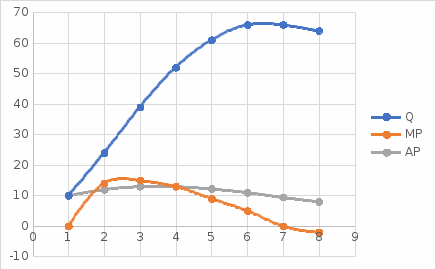 численное значение рабочей силы как вводимого фактора производства, максимизирующее предельный продукт – 3 численное значение рабочей силы как вводимого фактора производства, максимизирующее средний продукт – 3 и 4 численное значение рабочей силы как вводимого фактора производства, максимизирующее общий выпуск продукции – 6 и 7 Задание 3. Функция общих затрат компании, производящей галстуки, имеет вид ТС = 8 + 12Q – 6Q2 + Q3, где ТС- общие затраты (в сотнях долл. в месяц), а Q - объем производства (в сотнях галстуков в месяц). a. Каково уравнение для средних общих затрат? 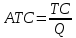 б. Каково уравнение для средних переменных затрат? 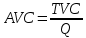 в. Каково уравнение для предельных затрат? 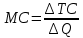 г. Заполните таблицу для колонок постоянных издержек (ТFС), переменных издержек (ТVС), общих издержек (TС), средних постоянных издержек (АFС), средних переменных издержек (АVС), средних общих издержек (АТС) и предельных издержек (МС) для значений Q от 1 до 5. Постройте кривые общих, переменных и постоянных затрат для значений Q. Постройте кривые АТС, АVС и МС для этих значений Q.
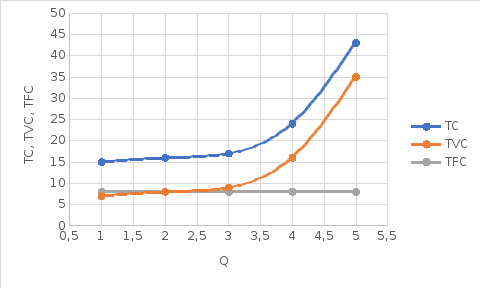 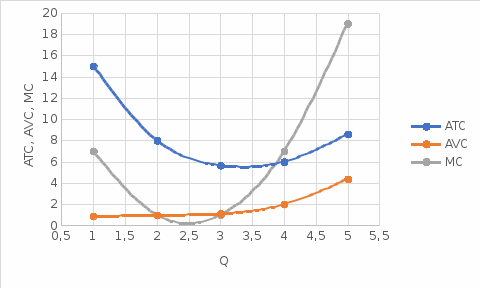 Задание 4. Проведите анализ безубыточности производства. Постройте график безубыточности по данным в таблице. 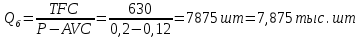 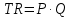 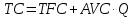 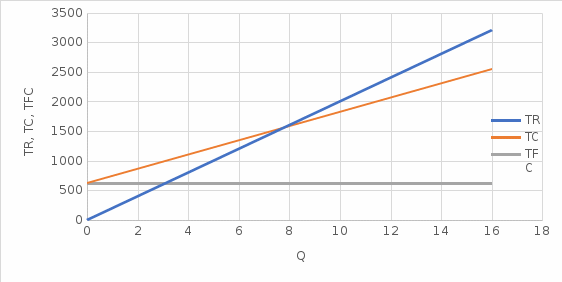 1. Рассчитайте, при каком объеме производства предприятие работает без прибыли и убытка. 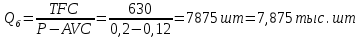 При объеме 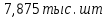 2. Цена изменяется на 10 % (а – уменьшается; б – увеличивается). Как изменяется прибыль? 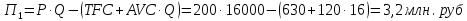 а – уменьшается 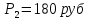 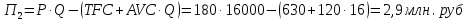 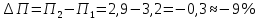 б – увеличивается 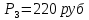 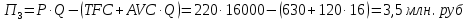 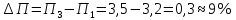 3. Оценить влияние 10 %-ного изменения (а – уменьшаются; б – увеличиваются) переменных расходов на прибыль. а – уменьшается 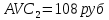 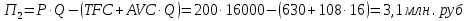 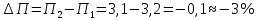 б – увеличивается 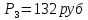 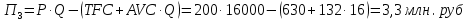 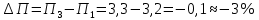 4. Оценить влияние 10 %-ного изменения (а – уменьшаются; б – увеличиваются) постоянных расходов на прибыль. а – уменьшается 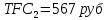 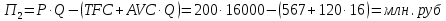 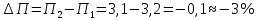 б – увеличивается 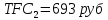 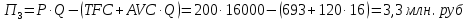 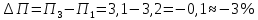 5. Оценить влияние 10 %-ного увеличения объема реализации на прибыль. 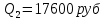 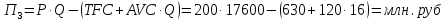 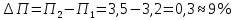 6. Сколько изделий необходимо продать для получения (300 + А×10) тыс. руб. прибыли? (А − последняя цифра номера зачетной книжки (студенческого билета) Если цифра равна нулю, необходимо взять число 10.) № 51200305 А=5 П=300+5*10=350 руб. П2=200Q+(630+120Q) 350=Q(200-120)+630=Q80+630 350-Q80-630=0 Q80=280 Q=3,5 тыс.шт – необходимо произвести для получения прибыли 350 тыс. руб. 3адание 5. Определить величину чистого дисконтированного дохода (NPV) и индекс доходности инвестиционного проекта по данным таблицы, тыс. руб. Дать оценку экономической эффективности проекта. Данные выбираются по номеру зачетной книжки (студенческого билета): А − последняя цифра; В − предпоследняя цифра; С − третья с конца цифра. Если цифра равна нулю, необходимо взять число 10. Рассчитанное по формуле значение занести в скобки. А = 5 В = 10 С = 3 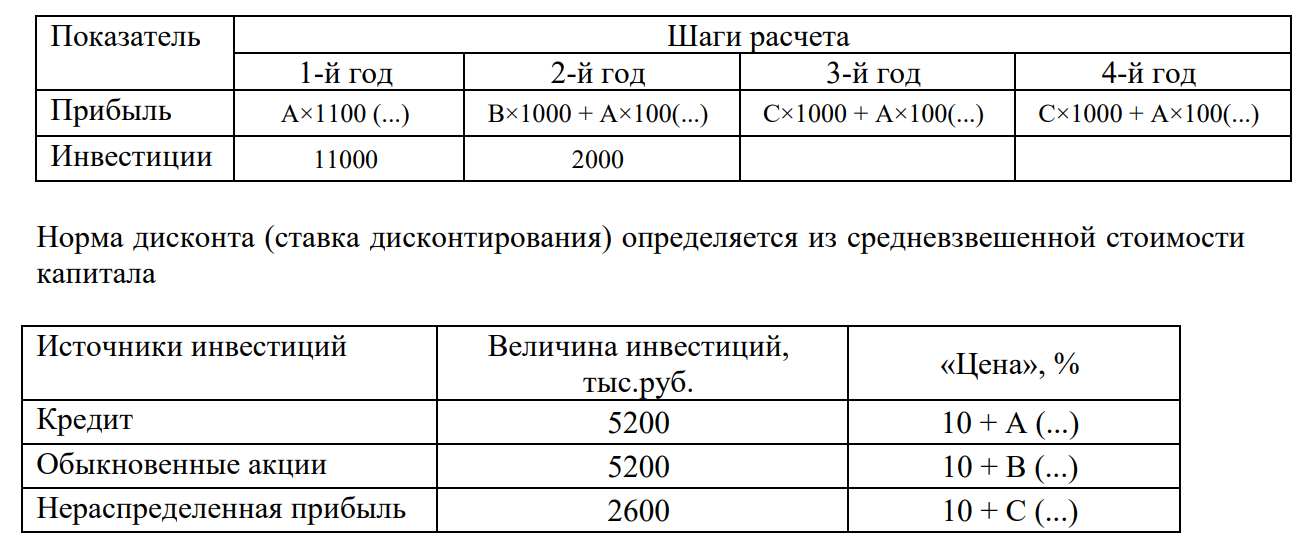 10+А=10+5=15% dкр=40% 10+В=10+10=20% dакц=40% 10+С=10+3=13% dпр=20% 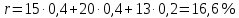
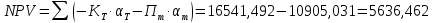 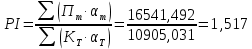 Проект эффективен, так как NPV больше нуля, PI больше единицы 3адание 6. Кондитерский цех изготавливает и продает торты. Заведующий производством цеха должен спрогнозировать спрос. На основе этого прогноза определите, сколько тортов следует выпекать и какова будет прогнозная прибыль. Проведенные исследования показывают, что спрос на торты за день составлял: 10 тортов – Ах10 (...) раз; 15 тортов – Вх15 (...) раз; 20 тортов – Сх15 (...) раз; 25 тортов – Вх10 (...) раз; 30 тортов – Сх10 (...) раз. Выпечка одного торта обходится цеху в Ах50 (...) руб., а продается он по цене Ах60 (...) руб. за штуку. Если кондитерское изделие не продается в течение дня, оно портится, а столовая несет убытки. Составить матрицу решения. Расписать расчет всех элементов матрицы и предполагаемой стоимости. Данные выбираются по номеру студенческого билета: А – последняя цифра; В – предпоследняя цифра; С – третья с конца цифра. Если цифра равна нулю, необходимо взять число 10. Рассчитанное по формуле значение занести в скобки.
10 тортов – Ах10 = 50 раз; 13% 15 тортов – Вх15 = 150 раз; 40% 20 тортов – Сх15 = 45 раз; 12% 25 тортов – Вх10 = 100 раз; 27% 30 тортов – Сх10 = 30 раз. 8% АТС = 5х50 = 250 руб Р = 5х60 = 300 руб
П = PQ-TC Вывод: при изготовлении 15 тортов мы получаем оптимальные продажи. 3адание 7. По оценке исследовательского отдела компании издержки, связанные с выпуском продукции (Q) можно выразить зависимостью TC = 53 + 4Q2. Цена на продукцию составляет 100 д. е. а. При каком значении Q прибыль становится максимальной? б. Каковы предельные поступления при этом значении Q? в. Каков максимальный уровень прибыли? 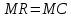 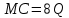 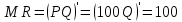 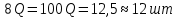 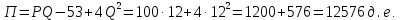 Ответы: 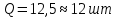 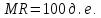 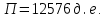 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||