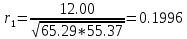Варианты 9, 10
|
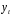
|
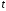
|
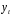
|
1
|
5,6
|
9
|
8,2
|
2
|
4,7
|
10
|
5,6
|
3
|
5,2
|
11
|
6,4
|
4
|
9,1
|
12
|
10,8
|
5
|
7,0
|
13
|
9,1
|
6
|
5,1
|
14
|
6,7
|
7
|
6,0
|
15
|
7,5
|
8
|
10,2
|
16
|
11,3
|
Требуется:
Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
Сделать прогноз на 2 квартала вперед.
Решение:
Построим поле корреляции:
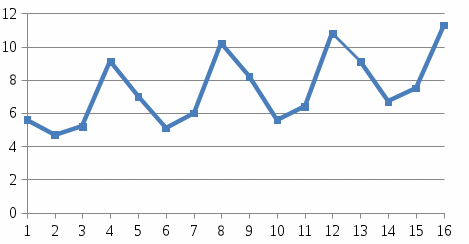
Рис.1. Поле корреляции
Уже исходя из графика видно, что значения y образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции.
Для этого составляем первую вспомогательную таблицу 2.
Таблица 2
t
|
yt
|
yt-1
|
yt-yt-1
|
yt-1-yt-2
|
(yt-y1)* (yt-1-y2)
|
(yt-y1)2
|
(yt-1-y2)2
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
5,6
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
4,7
|
5,6
|
-2,71
|
-1,10
|
2,98
|
7,32
|
1,21
|
3
|
5,2
|
4,7
|
-2,21
|
-2,00
|
4,41
|
4,87
|
4,00
|
4
|
9,1
|
5,2
|
1,69
|
-1,50
|
-2,54
|
2,87
|
2,25
|
5
|
7,0
|
9,1
|
-0,41
|
2,40
|
-0,98
|
0,17
|
5,76
|
6
|
5,1
|
7,0
|
-2,31
|
0,30
|
-0,69
|
5,32
|
0,09
|
7
|
6,0
|
5,1
|
-1,41
|
-1,60
|
2,25
|
1,98
|
2,56
|
8
|
10,2
|
6,0
|
2,79
|
-0,70
|
-1,96
|
7,81
|
0,49
|
9
|
8,2
|
10,2
|
0,79
|
3,50
|
2,78
|
0,63
|
12,25
|
10
|
5,6
|
8,2
|
-1,81
|
1,50
|
-2,71
|
3,26
|
2,25
|
11
|
6,4
|
5,6
|
-1,01
|
-1,10
|
1,11
|
1,01
|
1,21
|
12
|
10,8
|
6,4
|
3,39
|
-0,30
|
-1,02
|
11,52
|
0,09
|
13
|
9,1
|
10,8
|
1,69
|
4,10
|
6,94
|
2,87
|
16,81
|
14
|
6,7
|
9,1
|
-0,71
|
2,40
|
-1,70
|
0,50
|
5,76
|
15
|
7,5
|
6,7
|
0,09
|
0,00
|
0,00
|
0,01
|
0,00
|
16
|
11,3
|
7,5
|
3,89
|
0,80
|
3,12
|
15,16
|
0,64
|
Cумма
|
118,5
|
107,2
|
1,81
|
6,70
|
12,00
|
65,29
|
55,37
|
Среднее значение
|
7,41
|
6,70
|
|
|
|
|
|
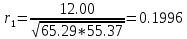
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка
Таблица 3
t
|
yt
|
yt-2
|
yt-y3
|
yt-2-y4
|
(yt-y3)* (yt-2-y4)
|
(yt-y3)2
|
(yt-2-y4)2
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
5,6
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
4,7
|
-
|
-
|
-
|
-
|
-
|
-
|
3
|
5,2
|
5,6
|
-2,21
|
-0,63
|
1,39
|
4,87
|
0,40
|
4
|
9,1
|
4,7
|
1,69
|
-1,53
|
-2,59
|
2,87
|
2,34
|
5
|
7,0
|
5,2
|
-0,41
|
-1,03
|
0,42
|
0,17
|
1,06
|
6
|
5,1
|
9,1
|
-2,31
|
2,87
|
-6,62
|
5,32
|
8,23
|
7
|
6,0
|
7,0
|
-1,41
|
0,77
|
-1,08
|
1,98
|
0,59
|
8
|
10,2
|
5,1
|
2,79
|
-1,13
|
-3,16
|
7,81
|
1,28
|
9
|
8,2
|
6,0
|
0,79
|
-0,23
|
-0,18
|
0,63
|
0,05
|
10
|
5,6
|
10,2
|
-1,81
|
3,97
|
-7,17
|
3,26
|
15,75
|
11
|
6,4
|
8,2
|
-1,01
|
1,97
|
-1,98
|
1,01
|
3,88
|
12
|
10,8
|
5,6
|
3,39
|
-0,63
|
-2,14
|
11,52
|
0,40
|
13
|
9,1
|
6,4
|
1,69
|
0,17
|
0,29
|
2,87
|
0,03
|
14
|
6,7
|
10,8
|
-0,71
|
4,57
|
-3,23
|
0,50
|
20,87
|
15
|
7,5
|
9,1
|
0,09
|
2,87
|
0,27
|
0,01
|
8,23
|
16
|
11,3
|
6,7
|
3,89
|
0,47
|
1,83
|
15,16
|
0,22
|
Cумма
|
118,5
|
99,7
|
4,51
|
12,46
|
-23,96
|
57,96
|
63,34
|
Среднее значение
|
7,41
|
6,23
|
|
|
|
|
|
|
 Скачать 192.71 Kb.
Скачать 192.71 Kb.