3 задачи 04.04.22. Среднедушевой прожиточный минимум в день одного трудоспособного, руб

Название	Среднедушевой прожиточный минимум в день одного трудоспособного, руб
Дата	12.10.2022
Размер	192.71 Kb.
Формат файла
Имя файла	3 задачи 04.04.22.docx
Тип	Документы #729840
страница	4 из 4

1 2 3 4

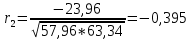Составляем вспомогательную таблицу для расчета коэффициента автокорреляции третьего порядка и т.д. получаем:

Лаг (порядок) – L	r_t,t-L	Коррелограмма
1	0,200	*
2	-0,395	*
3	0,223	**
4	0,861	****
5	0,268	*

Временной ряд содержит сезонные колебания периодичностью 4, т.к. объем потребления электроэнергии в первый-второй кварталы ниже, чем в третий-четвертый.

Рассчитаем компоненты мультипликативной модели временного ряда

Проведем выравнивание ряда скользящей средней

Таблица 4

№ квартала	yt	Итого за 4 квартала	скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оцентка сезонной компоненты
1	5,6	-	-	-	-
2	4,7	24,6	6,15	-	-
3	5,2	31,1	7,775	6,9625	0,75
4	9,1	32,4	8,1	7,9375	1,15
5	7,0	37,4	9,35	8,725	0,80
6	5,1	29,5	7,375	8,3625	0,61
7	6,0	30	7,5	7,4375	0,81
8	10,2	30,4	7,6	7,55	1,35
9	8,2	31	7,75	7,675	1,07
10	5,6	31,9	7,975	7,8625	0,71
11	6,4	33	8,25	8,1125	0,79
12	10,8	34,1	8,525	8,3875	1,29
13	9,1	34,6	8,65	8,5875	1,06
14	6,7	31,1	7,775	8,2125	0,82
15	7,5	-	-	-	-
16	11,3	-	-	-	-

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Эти оценки используются для расчета сезонной компоненты S

Таблица 5

Показатель	Номер квартала
	1	2	3	4
1	-	-	0,75	1,15
2	0,80	0,61	0,81	1,35
3	1,07	0,71	0,79	1,29
4	1,06	0,82	-	-
Всего за период	2,93	2,14	2,34	3,79
Среднее значение индексов	0,98	0,71	0,82	1,26
Корректирующий коэффициент	4/3,73=1,07
Скорректированный индекс	1,05	0,76	0,84	1,35
Сумма скорректированных индексов	4,00

Проверяем условие равенство 4 суммы значений сезонной компоненты:

1,05+0,76+0,84+1,35=4

Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины T*E=Y/S, которые содержат только тенденцию и случайную компоненту

Таблица 6

t	y_t	S_i	y_{t /Si}	T	T*S	E	E`	E²	e²
1	2	3	4	5	6	7	8	8	9
1	5,6	1,05	5,35	6,77	7,09	0,79	-1,49	2,23	6,37
2	4,7	0,76	6,15	6,59	5,03	0,93	-0,33	0,11	0,21
3	5,2	0,84	6,21	6,69	5,60	0,93	-0,40	0,16	1,06
4	9,1	1,35	6,73	7,51	10,15	0,90	-1,05	1,10	31,16
5	7,0	1,05	6,69	7,07	7,40	0,95	-0,40	0,16	8,01
6	5,1	0,76	6,68	6,67	5,10	1,00	0,00	0,00	0,28
7	6,0	0,84	7,17	6,86	5,74	1,05	0,26	0,07	1,37
8	10,2	1,35	7,54	7,74	10,46	0,97	-0,26	0,07	34,73
9	8,2	1,05	7,83	7,32	7,66	1,07	0,54	0,29	9,57
10	5,6	0,76	7,33	6,77	5,17	1,08	0,43	0,18	0,37
11	6,4	0,84	7,65	6,94	5,81	1,10	0,59	0,35	1,54
12	10,8	1,35	7,99	7,86	10,63	1,02	0,17	0,03	36,76
13	9,1	1,05	8,69	7,51	7,86	1,16	1,24	1,54	10,83
14	6,7	0,76	8,77	7,00	5,35	1,25	1,35	1,82	0,61
15	7,5	0,84	8,96	7,17	6,00	1,25	1,50	2,24	2,06
16	11,3	1,35	8,36	7,97	10,77	1,05	0,53	0,28	38,49
Итого	118,5		122,10	119,44	121,835265	23,49	2,66	7,10	183,43

Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T E.

При помощи МНК составим систему из двух уравнений с двумя неизвестными – параметрами а₀ и а₁: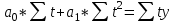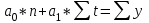

где у – исходный уровень ряда динамики,

n – число членов ряда,

t – показатель времени, который обозначается порядковыми номерами, начиная от низшего. Находим параметры уравнения методом наименьших квадратов.

Система уравнений МНК: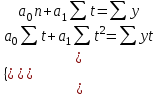

Для наших данных система уравнений имеет вид: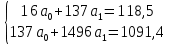

Из первого уравнения выражаем а₀ и подставим во второе уравнение

Получаем a₁ =0,21, a₀ = 5,60

Результаты аналитического выравнивания следующие:

T = 0,21t+5,60

Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты. На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели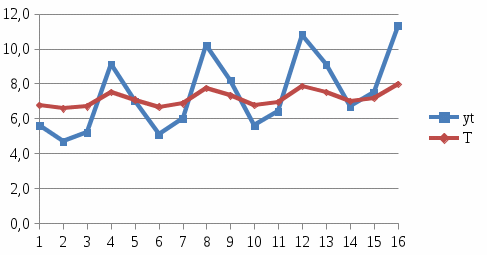

Рис.2. Исходные и прогнозные данные
Расчет ошибки в мультипликативной модели производится по формуле: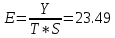

Рассчитаем коэффициент детерминации по формуле: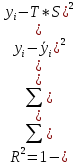

Прогнозирование по мультипликативной модели.

Если предположить, что по нашему примеру необходимо дать прогноз об общем объеме потребления электроэнергии на 17 и 18 кварталы, прогнозное значение Ft уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент.

Для определения трендовой компоненты воспользуемся уравнением тренда T = 0,21t+5,60

T₁₇=0.21*17+5.60=9.16

T₁₈=0.21*18+5.60=9.37

Значения сезонных компонент за соответствующие кварталы равны:

S₁=1,05

S₂=0,76

Таким образом

F17= T17*S1=9.16*1.05=9,59

F18= T18*S2= 9.37*0.76=7,15

т.е. в первые два квартала следовало ожидать порядка 9.59 и 7.15 объема потребления электроэнергии соответственно.

1 2 3 4