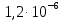Средняя интенсивность отказов для элементов системы

• Название: Средняя интенсивность отказов для элементов системы
• Дата: 10.03.2023
• Размер: 94.03 Kb.
• Имя файла: 1.docx
• Тип: Документы; #979828

Задание

При проектировании информационной системы следует обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97.
Исходные данные:

1. 
   Проектируемая система состоит из n элементов.
   
2. 
   Средняя интенсивность отказов для элементов системы – λ.
   
3. 
   Время, для которого определяется вероятность безотказной работы ИС – t.
   
4. 
   Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая.
   

При решении задачи необходимо определить:

1. 
   Как следует изменить количество элементов системы (n), чтобы надежность системы удовлетворяла поставленным требованиям?
   
2. 
   Как следует изменить надежность элементов системы (λ), чтобы надежность всей системы удовлетворяла поставленным требованиям?
   
3. 
   Как следует изменить время работы системы (t), чтобы надежность системы удовлетворяла поставленным требованиям?
   
4. 
   Построить графики зависимости надежности ИС от времени при различных значениях n, λ. Диапазон изменения времени функционирования – от 0 до 400, с шагом изменения – 25. Значения n выбрать равными - 50, 100, 200, 400, 800. Значения λ выбрать равными – 10^-5,
   

10^-6, 10^-7.

Вариант 1:

n	1200
λ (1/ч)
t (ч)	300

Выполнение

Исходные данные:n=1200, λ=1,2·10^-6 1/ч, t=300 ч.

Вероятность безотказной работы проектируемой системы (если не принимать дополнительных мер) составляет: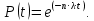




Вычислим P(t) учетом исходных данных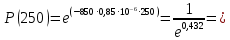

0,649209377

Полученное значение вероятности безотказной работы ИС не удовлетворяет поставленным требованиям P(300) ≥ 0,97.

Рассмотрим возможные способы повышения надежности проектируемой системы.

Для этого определим условия, при которых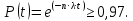



Решив последнее уравнение относительно параметров n, λ, t, получим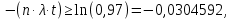



откуда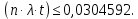



Обеспечить выполнение заданного требования по значению надежности ИС возможно, если n, при прочих равных условиях будет принимать следующие значения: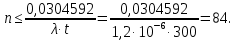



Результаты расчетов показывают, что для удовлетворения требований по значению вероятности безотказной работы ИС необходимо сократить количество элементов с 850 до 143.

Обеспечить выполнение требования по значению надежности ИС возможно, если повысить надежность входящих в систему элементов, при прочих равных условиях, до следующих значений: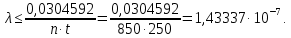



То есть, для удовлетворения требований по значению вероятности безотказной работы ИС необходимо повысить надежность входящих в состав системы элементов (уменьшить интенсивность отказов) практически в шесть раз.

Обеспечить выполнение требования по значению надежности ИС возможно, если уменьшить время работы системы, при прочих равных условиях, до следующих значений: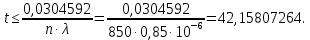



Как показывают результаты вычислений, обеспечить выполнение требования по значению надежности ИС возможно, если уменьшить время работы системы до величины 42 часов.

Для построения графиков зависимости значений вероятности безотказной работы ИС, определим следующие значения параметров:

- t_нач=0, t_кон=400, ∆t=25;

- n₁=50, n₂=100, n₃=200, n₄=400, n₅=800;

- λ₁=10^-5, λ₂=10^-6; λ₃=10^-7.

При использовании для построения графиков программы Excel вначале следует сформировать таблицы значений вероятности, которые в данном случае будут иметь следующий вид (табл. 2, 3, 4), соответствующие графики функции P(t) представлены на рис. 1, 2, 3.

Таблица 2

Расчетные значения вероятности безотказной ИС при λ=10^-5

t (ч)	P(t)=e-nλt (λ=10-5)
	n=50	n=100	n=200	n=400	n=800
0	1	1	1	1	1
25	0,9875778	0,975309912	0,951229425	0,904837418	0,818730753
50	0,975309912	0,951229425	0,904837418	0,818730753	0,670320046
75	0,963194418	0,927743486	0,860707976	0,740818221	0,548811636
100	0,951229425	0,904837418	0,818730753	0,670320046	0,449328964
125	0,939413063	0,882496903	0,778800783	0,60653066	0,367879441
150	0,927743486	0,860707976	0,740818221	0,548811636	0,301194212
175	0,916218872	0,839457021	0,70468809	0,496585304	0,246596964
200	0,904837418	0,818730753	0,670320046	0,449328964	0,201896518
225	0,893597347	0,798516219	0,637628152	0,40656966	0,165298888
250	0,882496903	0,778800783	0,60653066	0,367879441	0,135335283
275	0,87153435	0,759572123	0,57694981	0,332871084	0,110803158
300	0,860707976	0,740818221	0,548811636	0,301194212	0,090717953
325	0,85001609	0,722527354	0,522045777	0,272531793	0,074273578
350	0,839457021	0,70468809	0,496585304	0,246596964	0,060810063
375	0,829029118	0,687289279	0,472366553	0,22313016	0,049787068
400	0,818730753	0,670320046	0,449328964	0,201896518	0,040762204

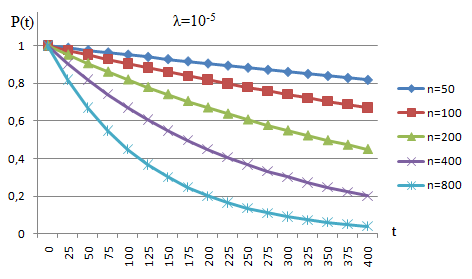Рис. 1. График значений вероятности безотказной работы ИС согласно табл. 2

Таблица 3

Расчетные значения вероятности безотказной ИС при λ=10^-6

t (ч)	P(t)=e-nλt (λ=10-6)
	n=50	n=100	n=200	n=400		n=800
0	1	1	1		1	1
25	0,998750781	0,997503	0,995012479		0,990049834	0,980198673
50	0,997503122	0,995012	0,990049834		0,980198673	0,960789439
75	0,996257022	0,992528	0,98511194		0,970445534	0,941764534
100	0,995012479	0,99005	0,980198673		0,960789439	0,923116346
125	0,993769491	0,987578	0,975309912		0,951229425	0,904837418
150	0,992528055	0,985112	0,970445534		0,941764534	0,886920437
175	0,99128817	0,982652	0,965605416		0,93239382	0,869358235
200	0,990049834	0,980199	0,960789439		0,923116346	0,852143789
225	0,988813045	0,977751	0,955997482		0,913931185	0,835270211
250	0,9875778	0,97531	0,951229425		0,904837418	0,818730753
275	0,986344099	0,972875	0,946485148		0,895834135	0,802518798
300	0,98511194	0,970446	0,941764534		0,886920437	0,786627861
325	0,983881319	0,968022	0,937067463		0,878095431	0,771051586
350	0,982652236	0,965605	0,93239382		0,869358235	0,755783741
375	0,981424688	0,963194	0,927743486		0,860707976	0,740818221
400	0,980198673	0,960789	0,923116346		0,852143789	0,726149037

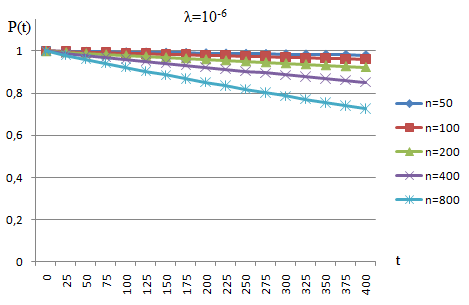Рис. 2. График значений вероятности безотказной работы ИС согласно табл. 3

Таблица 4

Расчетные значения вероятности безотказной ИС при λ=10^-7

t (ч)	P(t)=e-nλt (λ=10-7)
	n=50	n=100	n=200	n=400	n=800
0	1	1	1	1	1
25	0,999875	0,99975	0,9995	0,999	0,998002
50	0,99975	0,9995	0,999	0,998002	0,996008
75	0,999625	0,99925	0,998501	0,997004	0,994018
100	0,9995	0,999	0,998002	0,996008	0,992032
125	0,999375	0,998751	0,997503	0,995012	0,99005
150	0,99925	0,998501	0,997004	0,994018	0,988072
175	0,999125	0,998252	0,996506	0,993024	0,986098
200	0,999	0,998002	0,996008	0,992032	0,984127
225	0,998876	0,997753	0,99551	0,99104	0,982161
250	0,998751	0,997503	0,995012	0,99005	0,980199
275	0,998626	0,997254	0,994515	0,98906	0,97824
300	0,998501	0,997004	0,994018	0,988072	0,976286
325	0,998376	0,996755	0,993521	0,987084	0,974335
350	0,998252	0,996506	0,993024	0,986098	0,972388
375	0,998127	0,996257	0,992528	0,985112	0,970446
400	0,998002	0,996008	0,992032	0,984127	0,968507

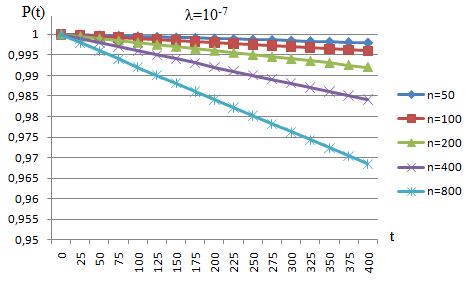Рис. 3. График значений вероятности безотказной работы ИС согласно табл. 4