метод указаний. Метод указания_Таблица сопряженности. Срсп анализ качественных признаков. Таблицы сопряженности
 Скачать 41.59 Kb. Скачать 41.59 Kb.
|
СРСП - Анализ качественных признаков. Таблицы сопряженностиСуществует множество признаков, различных явлений и вещей, измерение которых затруднено или вовсе невозможно. Например, как измерить признак «профессия» или «вид патологии», а как сравнить эти признаки для получения статистического представления о профессиональной заболеваемости? В этих случаях изучается распространенность признаков, частота встречаемости признаков (доля объектов с интересующим нас признаком) в различных выборках, оценивается взаимосвязь частоты встречаемости одного признака с частотой встречаемости другого признака. Для этого используются таблицы сопряженности. Столбцы этой таблицы обозначают градации одного признака, строки – градации другого признака. В каждой ячейке записывается число случаев с сопряженными признаками. Наиболее простой случай таблица 2х2 (исследуется частота совместного распространения двух признака, каждый из которых имеет две градации). В общем случае Н(0) формулируется следующим образом: в генеральных совокупностях доля объектов с интересующими нас признаками одинакова или частота встречаемости одного признака не зависит от частоты встречаемости другого признака или какой-либо фактор не влияет на частоту встречаемости признака (признаков) СЛУЧАЙ 1. Выборки независимые Предположим, что у нас есть два качественных признака, характеризующие обследованных лиц. Занесем эти данные в таблицу сопряженности
Критерием для проверки нулевой гипотезы является хи-квадрат Пирсона с поправкой Йетса 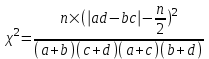 Его критическое значение находится для заданного уровня значимости α и числа степеней свободы f=(m-1)(n-1), где m-число столбцов, n – число строк (Приложение 5). Если 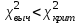 то Н(0) принимается, то Н(0) принимается, В случае 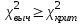 принимается Н(1) принимается Н(1)Можно вычислить меру связи между двумя признаками – ею является коэффициент ассоциации Юла Q(аналог коэффициента корреляции) 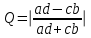 Qлежит в пределах от 0 до 1. Близкий к единице коэффициент свидетельствует о сильной связи между признаками. При равенстве его нулю – связь отсутствует. Работа с преподавателем Руководствуясь тем, что аспирин препятствует образованию тромбов, Г. Харатер решил проверить, нельзя ли снизить риск тромбоза назначением небольших доз аспирина (160 мг/сут.). Было проведено контролируемое испытание. Все больные, согласившиеся принять участие в испытании и не имевшие противопоказаний к аспирину, были случайным образом разделены на две группы: 1-я получала плацебо, 2-я - аспирин. Исследование проводилось до тех пор, пока общее число больных с тромбозом шунта не достигло 24. Группы практически не различались по возрасту, полу и продолжительности лечения гемодиализом. В 1-й группе тромбоз шунта произошел у 18 из 25 больных, во 2-й -у 6 из 19. Можно ли говорить о статистически значимом различии доли больных тромбозом, а тем самым об эффективности аспирина? Зададим уровень значимости α=0,05 Сформулируем Н(0): в генеральной совокупности доля больных тромбозом не зависит от приема аспирина. Занесем результаты испытания в таблицу.
Посчитаем значение критерия хи-квадрат с поправкой Йетса 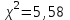 Q=0,7 Мы задали 5% -ный уровень значимости α = 0,05 . Тогда критическое значение = 3,84 (по таблице для f=1). Полученное значение χ2=5,56 больше, чем критическое, следовательно, мы отвергаем Н(0) гипотезу о том, что аспирин не влияет на проявление тромбоза шунта. Следовательно, мы можем утверждать с вероятностью 95%, что использование аспирина эффективно снижает риск тромбоза в генеральной совокупности. Q=0,7 показывает сильную связь между приемом аспирина и вероятностью тромбоза. Случай 2. Выборки зависимые Над одними и теми же объектами проводятся два наблюдения: до и после. (прием лекарства, обучение, внушение и т.д.) Подсчитывается сколько раз данное свойство встречается: и «до» и «после», (+,+) только «до» (+,-) только «после» (-,+) ни «до» ни «после» (-,-)
Н(0) – доля объектов с интересующим нас признаком «после» не изменилась по сравнению с «до» Вычисляем критерий хи-квадрат Мак-Нимара 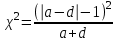 Если 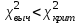 то Н(0) принимается то Н(0) принимаетсяЕсли 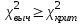 то принимаем Н(1), то принимаем Н(1), Работа с преподавателем. Было проведено исследование эффективности антитабачной рекламы. Для этого сравнили соотношение курящих/некурящих до и после проведения рекламной компании. Сформулируем Н(0): рекламная компания, проведенная в генеральной совокупности, не повлияет на долю курящих. Или - соотношение курящих и некурящих среди членов генеральной совокупности после рекламной компании не изменится. Зададим уровень значимости α=0,01 Рекламная компания была проведена среди 100 человек. В результате исследования были получены следующие результаты
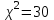 Мы задали 1% -ный уровень значимости α = 0,01 . Тогда критическое значение = 6,64 (по таблице для f=1). Полученное значение χ2=30 больше, чем критическое, следовательно: мы отвергаем нулевую гипотезу и принимаем альтернативную о том, что с вероятностью 99 % рекламная компания повлияет на соотношение курящих и некурящих в популяции (генеральной совокупности). Контрольные вопросы Для каких целей используются таблицы сопряженности Структура таблицы сопряженности Сформулирйте нулевую гипотезу для общего случая Какие данные заносятся в таблицу сопряженности в случае зависимых выборок Какие критерии используются при анализе таблицы сопряженности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
