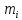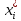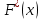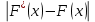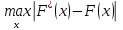Математическая статистика. Задачи. Статистическая обработка выборочных данных
 Скачать 68.15 Kb. Скачать 68.15 Kb.
|
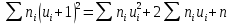 , 283=283 , 283=283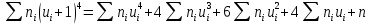 , 7207=7207, , 7207=7207,совпадение контрольных сумм свидетельствует о правильности вычислений. Вычислим условные моменты первого, второго, третьего и четвертого порядков: 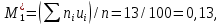 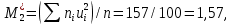 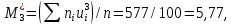 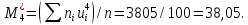 Вычислим центральные эмпирические моменты третьего и четвертого порядков 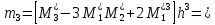 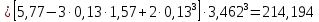 , ,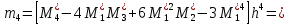 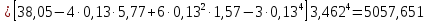 . .Определим искомые значения выборочных среднего, дисперсии, асимметрии и эксцесса: 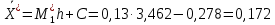 , ,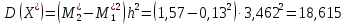 , ,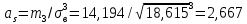 , ,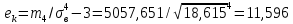 . .Построим гистограмму и график эмпирической функции распределения. 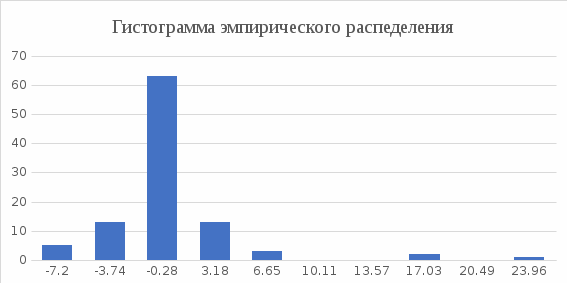 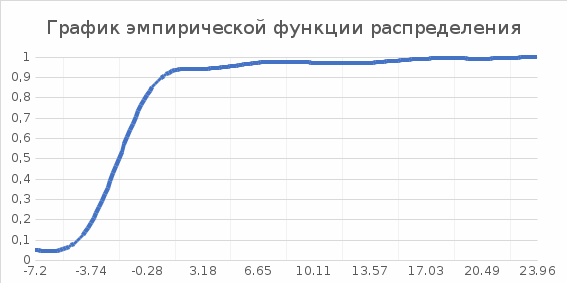 4. Для выборочного среднего доверительный интервал с надежностью 0,95 определяется выражением: 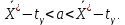 При неизвестном 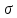 определим определим 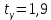 по приложению 2 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] с параметрами по приложению 2 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] с параметрами 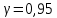 и и 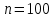 . Таким образом, доверительные интервалы для выборочного среднего представим в виде: . Таким образом, доверительные интервалы для выборочного среднего представим в виде: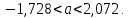 Для построения доверительного интервала дисперсии с надежностью 0,95 воспользуемся приложением 4 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] и определим 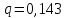 (входом в приложение являются параметры (входом в приложение являются параметры 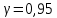 и и 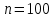 . Так как . Так как 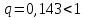 , доверительный интервал определяется выражением: , доверительный интервал определяется выражением: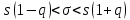 где 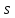 – исправленная выборочное среднее квадратическое отклонение: – исправленная выборочное среднее квадратическое отклонение: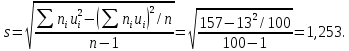 Таким образом, доверительные интервалы для выборочного среднего квадратического отклонения представим в виде: 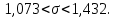 5. Выдвинем статистическую гипотезу о соответствии выборочного закона распределения распределению Коши с параметрами 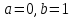 : :Теоретическая функции распределения Коши определяется выражением: 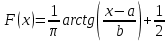 Или в соответствии с заданными параметрами: 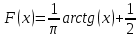 Для проверки гипотезы методом К. Пирсона результаты испытаний представим в виде таблицы (смотри пункт 2) и дополним их вероятностями 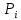 попадания случайной величины попадания случайной величины 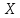 в соответствии с теоретическим законом распределения в в соответствии с теоретическим законом распределения в 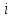 -ый интервал: -ый интервал: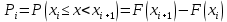
В качестве показателя согласованности используем случайную величину 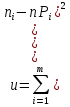 где 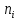 - число результатов испытаний, попавших в - число результатов испытаний, попавших в 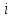 -ый интервал; -ый интервал; 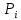 - вероятность попадания результата испытания в - вероятность попадания результата испытания в 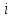 -ый интервал при теоретическом законе распределения исследуемой переменной -ый интервал при теоретическом законе распределения исследуемой переменной 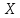 . .Вычислим значение показателя согласованности 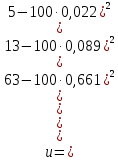 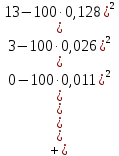 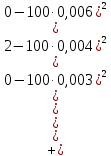 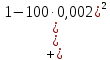 Показатель согласованности имеет 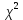 -распределение с числом степеней свободы -распределение с числом степеней свободы 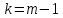 , где , где 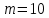 – количество интервалов разбиения эмпирических данных. – количество интервалов разбиения эмпирических данных. При требуемом уровне значимости ( 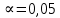 ) и числом степеней свободы ) и числом степеней свободы 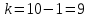 определим в соответствии с приложением 5 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] значение определим в соответствии с приложением 5 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] значение 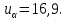 В качестве критической целесообразно выбрать правостороннюю критическую область 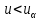 . .Так как неравенство 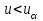 не выполняется то гипотезе о том, что эмпирическое распределение подчиняется закону Коши бракуется. не выполняется то гипотезе о том, что эмпирическое распределение подчиняется закону Коши бракуется.При проверке гипотез методом А.Н. Колмогорова в качестве показателя согласованности принимают случайную величину 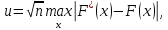 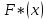 , , 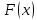 - эмпирическая и теоретическая функции распределения исследуемой случайной переменной - эмпирическая и теоретическая функции распределения исследуемой случайной переменной 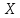 . .Независимо от вида закона распределения случайной переменной 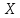 функция распределения показателя согласованности имеет вид функция распределения показателя согласованности имеет вид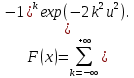 В качестве критической области используется правосторонняя область, границу  которой определяют из условия которой определяют из условия 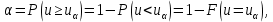 то есть она равна 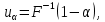 При требуемом уровне значимости ( 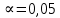 ) ) 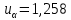 Определим максимальную величину модуля разности ординат эмпирической и теоретической функций распределения и вычислим значение показателя согласованности 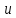 : :
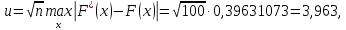 Так как неравенство 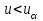 не выполняется то гипотеза о соответствии выборочного закона распределения распределению Коши с параметрами не выполняется то гипотеза о соответствии выборочного закона распределения распределению Коши с параметрами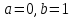 отклоняется. отклоняется.6. Даны значения трёх факторов X, Y, Z каждый на двух уровнях (всего 8 наборов значений), для каждого из них известно экспериментальное значение W. На основе исходных данных план полного факторного эксперимента оформим в виде матрицы планирования.
Линейное уравнение регрессии представим в виде полинома: 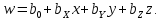 Данный полином содержит один свободный член 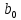 и 3 линейных члена и 3 линейных члена 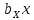 , , 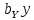 , , 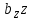 . Вычислим соответствующие коэффициенты регрессии: . Вычислим соответствующие коэффициенты регрессии: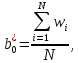 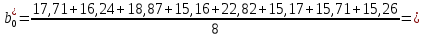 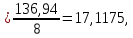 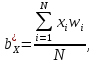 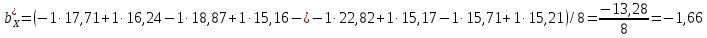 По аналогии с оценкой коэффициента регрессии  , найдем остальные: , найдем остальные: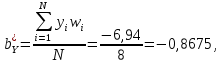 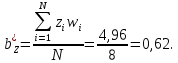 Таким образом линейное уравнение регрессии примет вид: 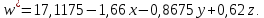 Литература 1. Гмурман В.Е. Руководство к решению задач по теории вероятностей, математической статистике и случайным функциям. М., 2002. 2. Ткачев А.Н., Некрасов С.А. Теория вероятностей и ее приложения. Учебное пособие. На компьютерном носителе (сервер лаборатории ЭВМ кафедры ПМ). 3. Ткачев А.Н., Некрасов С.А. Теория вероятностей и ее приложения. Учебное пособие. Новочеркасск, ЮРГТУ (НПИ), 2007. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||