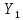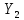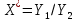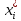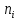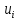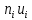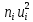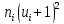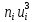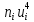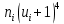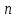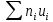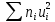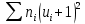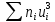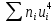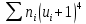Математическая статистика. Задачи. Статистическая обработка выборочных данных
 Скачать 68.15 Kb. Скачать 68.15 Kb.
|
2. Сгруппируем данные выборки и построим таблицу соответствующего статистического ряда. Найдем минимальное и максимальное значение в выборке: 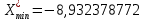 , , 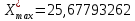 Разобьем полученный интервал на 10 равных и полученное значение шага округлим до тысячных в большую сторону: 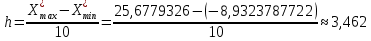 Получим следующие границы интервалов взяв за левую границу первого интервала минимальное значение, округленное до тысячных в большую по модулю сторону: 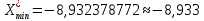
Округление в большую по модулю сторону позволяет учесть все 100 значений выборки. Определим значения вариант (середин интервалов) и частоту попадания значений выборки в данные интервалы:
3. Так-как варианты являются равноотстоящими, для вычисления выборочных среднего, дисперсии, асимметрии и эксцесса удобно воспользоваться методом произведений, то есть использовать следующие формулы: 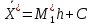 , , 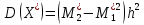 , , 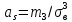 , , 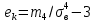 , ,где 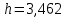 – шаг (разность между двумя соседними вариантами); С – ложный нуль (выберем варианту (-0,278), которая имеет наибольшую частоту); – шаг (разность между двумя соседними вариантами); С – ложный нуль (выберем варианту (-0,278), которая имеет наибольшую частоту); 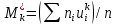 – условные моменты – условные моменты 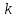 -го порядка; -го порядка; 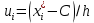 – условная варианта; – условная варианта; 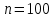 общий объем выборки; общий объем выборки; 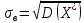 – выборочное среднее квадратическое отклонение; – выборочное среднее квадратическое отклонение; 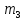 и и 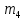 – центральные эмпирические моменты третьего и четвертого порядков которые в случае равноотстоящих вариант удобно вычислять по формулам: – центральные эмпирические моменты третьего и четвертого порядков которые в случае равноотстоящих вариант удобно вычислять по формулам: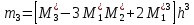 , , 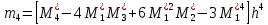 . .Составим расчетную таблицу:
Столбцы 6 и 9 служат для контроля вычислений с помощью тождеств: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||