М_В3_Заказ_5095391_13_12_22. Статистическая
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
1 2 П 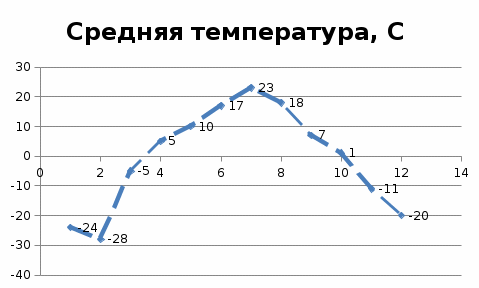 остроим график остроим графикИз 100 учеников старших классов все изучают английский, французский или немецкий языки. Английский изучают 70 учащихся, французский – 65, немецкий – 50, английский и немецкий – 3, английский и французский – 40, французский и немецкий – 20. Сколько учеников изучают все три языка? Решение. При решении задачи будем использовать круги Эйлера. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знает немецкий. Все три круга пересекаются. Универсальное множество U – это множество всех учеников старших классов. 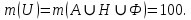 А – множество учащихся, изучающих английский язык; Н – множество учащихся, изучающих немецкий язык; Ф – множество учащихся, изучающих французский язык. 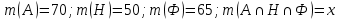 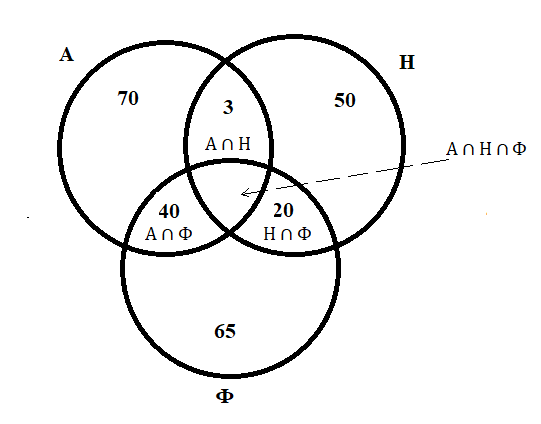 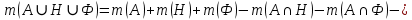 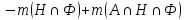 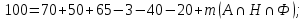 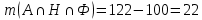 Получаем, что все три языка изучают 22 учащихся старших классов Семья, состоящая из отца А, матери В и трех дочерей С. Д. Е купила телевизор. Условились, что в первый вечер будут смотреть передачи в таком порядке: Когда отец А смотрит передачу, то мать В делает то же. Дочери Д и Е, обе или одна из них, смотрят передачу. Из двух членов семьи – мать В и дочь С – смотрят передачу одна и только одна. Дочери С и Д или обе смотрят передачу, или обе не смотрят. Если дочь Е смотрит передачу, то отец A и дочь Д делают то же. Кто же из членов семьи в этот вечер смотрит передачу? Решение. Составим сложное высказывание: F (A, B, C, D, E) = (A→B)∧(D∨E)∧(B⊕C)∧(C↔D)∧(E→A)∧(E→D) Выясним, на каком наборе переменных это высказывание истинно. Составим таблицу истинности. При заполнении будем учитывать, что высказывание F истинно тогда и только тогда, когда истинны все входящие в него «подвысказывания» между операциями конъюнкции, поэтому в некоторых случаях можно сразу указать, на каких наборах F принимает ложное значение. Высказывание A→B принимает ложные значения, когда А истинно, а В ложно, поэтому на наборах №№17 – 24 оно ложно, следовательно, ложно и F. Высказывание (D∨E) принимает ложные значение, когда и D, и Е ложно, поэтому на наборах №№1, 5, 9, 13, 17, 21, 25, 29 оно ложно, следовательно, ложно и F. Высказывание (B⊕C) принимает ложные значение, когда В и С одновременно или истинны, или ложны, поэтому на наборах №№1 – 4, 13 – 20, 29 - 32 оно ложно, следовательно, ложно и F. Высказывание C↔D принимает ложные значение, когда или С истинно и D ложно, или С ложно и D истинно, поэтому на наборах №№3 – 6, 11 – 14, 19 – 22, 27 – 30 оно ложно, следовательно, ложно и F. Высказывание (E→A) принимает ложные значения, когда Е истинно, а А ложно, поэтому на наборах №№2, 4, 6, 8, 10, 12, 14, 16 оно ложно, следовательно, ложно и F. Высказывание (E→D) принимает ложные значения, когда Е истинно, а D ложно, поэтому на наборах №№ 2, 6, 10, 14, 18, 22, 26, 30. оно ложно, следовательно, ложно и F.
Видно, что высказывание принимает истинное значение на единственном наборе №7, т.е. дочери С и D смотрят телевизор, остальные нет. Автобусные билеты имеют шестизначные номера от 000000 до 999999. сколько номеров, у которых есть хотя бы одна нечетная цифра? сколько номеров содержат цифру 7? сколько номеров содержат цифру 7 и 0? сколько среди них счастливых? (Счастливым считается номер abcabc или abccba). Решение. Сначала найдем количество номеров, все цифры которых чётны. Сначала поставим на первое место одну из 5 чётных цифр, это можно сделать пятью способами. Для каждого из этих способов есть по пять возможностей поставить чётную цифру на второе место, затем на третье, и т.д.. Всего получается 5·5·5·5·5·5 = 56 = 15625 способов составить шестизначный номер только из чётных цифр. Т.о, во всех остальных номерах будет хотя бы одна нечетная цифра, т.е. 1 000 000 – 15625 = 984 375. Количество билетов, не содержащих цифру 7: на первом месте может быть любая цифра, кроме 7, на втором, любая кроме 7, на третьем тоже кроме одной (7), и так далее. Итого билетов, не содержащих цифру 7: 9*9*9*9*9*9 = 96 = 531441. Т.о, во всех остальных номерах будет хотя бы одна цифра 7, т.е. 1 000 000 – 531441 = 468 559. Возьмём все шестизначные номера билетов = 1000000 и вычтем из них все, в которых нет 7 и нуля. Это цифры 1 2 3 4 5 6 8 9. Перемножаем все варианты 8*7*6*5*4*3 = 20160 Т.о, во всех остальных номерах будет хотя бы одна цифра 7 или 0, т.е. 1 000 000 – 20160 = 979 840 . Количество билетов вида abcabc: на первом месте может быть любая цифра, на втором, любая, на третьем тоже любая, на четвертом – 1 (такая же как на первом), на пятом 1, на шестом 1. Итого билетов вида abcabc: 10*10*10*1*1*1 = 103 = 1000. Количество билетов вида abccba: на первом месте может быть любая цифра, на втором, любая, на третьем тоже любая, на четвертом – 1 (такая же как на третьем), на пятом 1, на шестом 1. Итого билетов вида abccba: 10*10*10*1*1*1 = 103 = 1000. Т.о. количество счастливых билетов 1000 + 1000 = 2000. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве 25 с первого завода, 35 со второго, 40 с третьего. Вероятность качественного изготовления изделий на первом заводе 0,9, на втором 0,8, на третьем 0,7. Какова вероятность того, что взятое случайным образом изделие будет качественным? Решение Обозначим: Н1 – это событие, состоящее в том, что наугад взятое комплектующее изготовлено на первом заводе; Н2 – это событие, состоящее в том, что наугад взятое комплектующее изготовлено на втором заводе; Н3 – это событие, состоящее в том, что наугад взятое комплектующее изготовлено на третьем заводе. Н1, Н2 и Н3 - гипотезы; образуют полную группу событий. По условию задачи априорные вероятности гипотез: P(H1) = 25/(25 + 35 + 40) = 0,25 P(H2) = 35/(25 + 35 + 40) = 0,35 P(H3) = 40/(25 + 35 + 40) = 0,40 Обозначим А - событие, состоящее в том, что взятое случайным образом изделие качественное. Условные вероятности: P(A|H1) = 0,9 P(A|H2) = 0,8 P(A|H3) = 0,7 Тогда, используя формулу полной вероятности, получаем P(A) = P(H1) · P(A|H1) + P(H2) · P(A|H2) + P(H3) · P(A|H3) = = 0,25·0,9 + 0,35·0,8 + 0,4·0,7 = 0,815 Ответ: 0,815 В классе 24 человека. Получены следующие результаты педагогического измерения.
Р 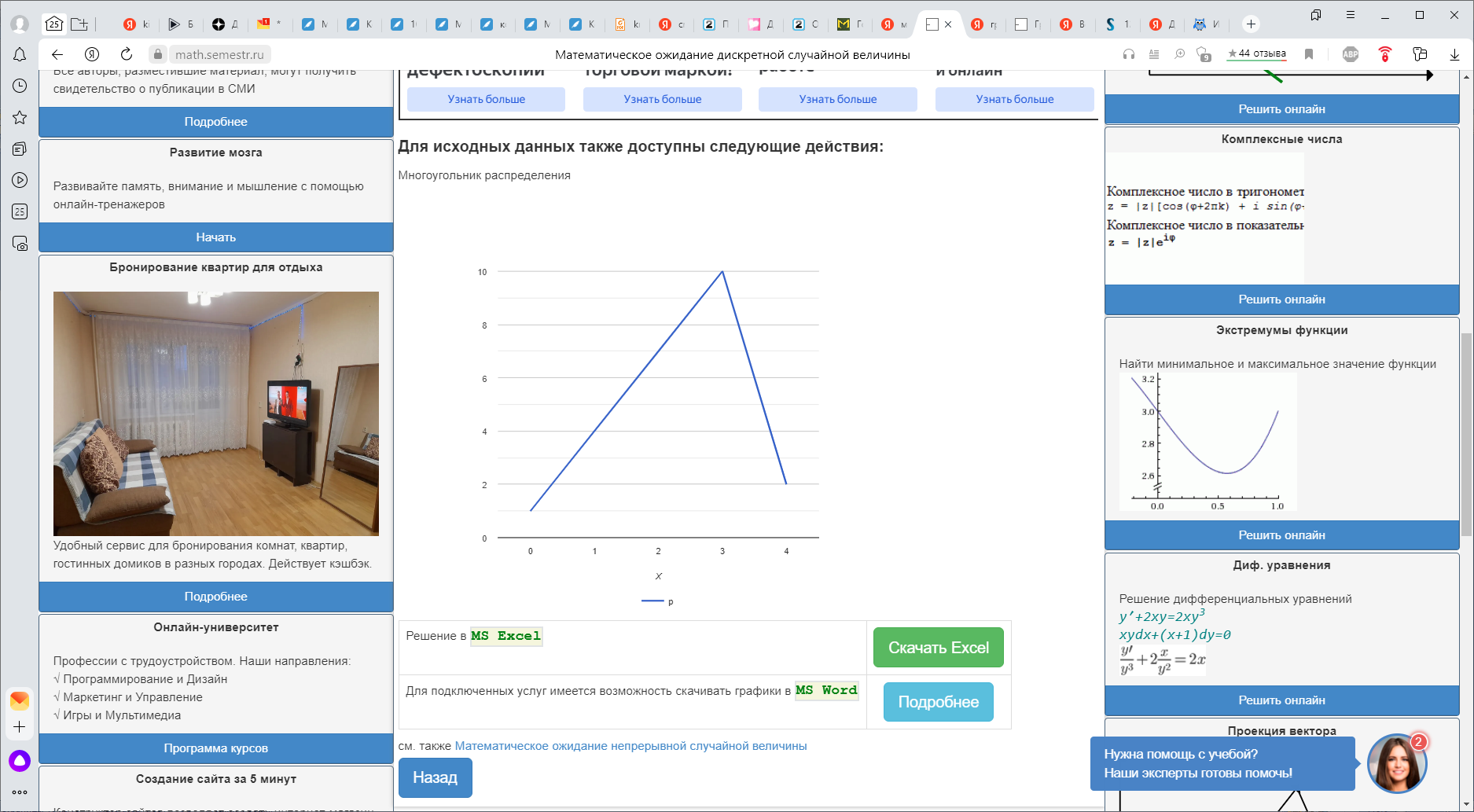 ассчитайте числовые характеристики данного распределения (математическое ожидание, выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, моду). Оформите результаты в виде полигона относительных частот. Решение. На основе исходных данных построим полигон частот Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. В классе из 24 человек наиболее часто встречаются с уровнем выше среднего - 10 учеников. На основе статистического распределения (ряда) получим выборочное распределение:
П 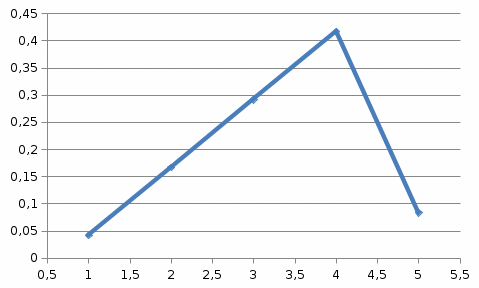 олигон относительных частот олигон относительных частотМатематическое ожидание находим по формуле m = ∑xipi. M[x] = 0∙0,0417 + 1∙0,167 + 2∙0,292 + 3∙0,417 + 4∙0,0833 = 2,333 Получили средний уровень подготовки класса. Дисперсию находим по формуле D = ∑x2ipi - M[x]2. D[X] = 02∙0,0417 + 12∙0,167 + 22∙0,292 + 32∙0,417 + 42∙0,0833 – 2,3332 = 0,972. Среднее квадратическое отклонение σ(x). 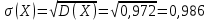 На фирме работает 40 человек. Проведено исследование числа рабочих дней, пропущенных каждым работником фирмы в течение месяца. Результаты этого исследования таковы: 0, 2, 5, 10, 5, 1, 9, 15, 10, 1, 0, 0, 2, 3, 5, 7, 3, 5, 2, 10, 7, 10, 7, 5, 2, 3, 5, 7, 10, 13, 0, 7, 6, 5, 3, 0, 3, 0,1, 3. Составить, вариационный ряд, найти моду, медиану и размах вариационного ряда. Составить интервальный вариационный ряд. Построить функцию распределения случайной величины числа пропущенных рабочих дней. Решение. Ранжируем числовой ряд: 0, 0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 6, 7, 7, 7, 7, 7, 9, 10, 10, 10, 10, 10, 13, 15. Построим дискретный вариационный ряд:
xi - число рабочих дней, пропущенных каждым работником фирмы в течение месяца. ni – количество работников. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
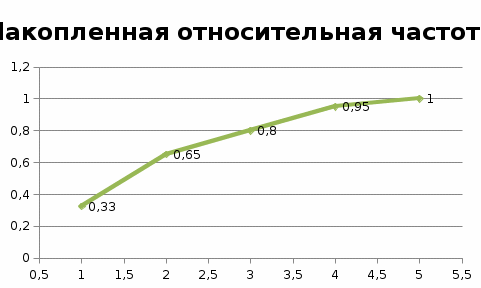
Наиболее часто встречаются работники с 5 пропущенными рабочими днями. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Имеем ранжированный исходный ряд: 0, 0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 6, 7, 7, 7, 7, 7, 9, 10, 10, 10, 10, 10, 13, 15. N = 40, середина ряда – 20 и 21 элементы. Для определения медианы вычисляем их среднее арифметическое: х20 = 5; х21 = 5. Таким образом, медиана равна 5. Половина рабочих имеет количество пропущенных рабочих дней менее 5, половина – более 5. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 15 - 0 = 15. Составим интервальный вариационный ряд Число групп приближенно определяется по формуле Стэрджесса n = 1 + 3,322log n = 1 + 3,322log(40) = 5 Ширина интервала составит: 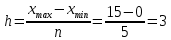 xmax - максимальное значение группировочного признака в совокупности. xmin - минимальное значение группировочного признака. Результаты группировки оформим в виде таблицы:
 1 2 |
