Главная страница
Навигация по странице:

  • Таблица 2 Описательные статистики

  • Таблица 3 Результаты полной объясненной дисперсии

    		•

    просветление. Статистический анализ безработицы в Российской Федерации


    Скачать 162.43 Kb.
    НазваниеСтатистический анализ безработицы в Российской Федерации
    Анкорпросветление
    Дата29.03.2022
    Размер162.43 Kb.
    Формат файлаdocx
    Имя файлапросветление.docx
    ТипДокументы
    #425666
    страница6 из 7
    1   2   3   4   5   6   7

    Глава 3. Статистический анализ безработицы в Российской Федерации



    3.1. Факторы, оказывающие влияние на уровень безработицы в России


    Перед тем как переходить непосредственно к анализу данных, необходимо предварительно выбрать факторы, которые на первый взгляд могут оказывать влияние на уровень безработицы. Для исследования были взяты данные Росстата за 2011 год с целью анализа текущих тенденций на рынке труда.

    Первоначально были отобраны следующие социально-экономические факторы, принимая во внимания результаты исследований, проведенных ранее:

    1. среднее время поиска работы безработными (месяцев);

    2. удельный вес убыточных организаций (в процентах от общего числа организаций);

    3. удельный вес городского населения в общей численности населения (оценка на конец года, в процентах);

    4. коэффициенты пенсионной нагрузки (оценка на конец года);

    5. общие коэффициенты рождаемости (число родившихся на 1000 человек населения);

    6. ожидаемая продолжительность жизни при рождении (число лет);

    7. общие коэффициенты брачности на 1000 человек населения;

    8. коэффициенты миграционного прироста на 10000 человек населения;

    9. индекс физического объема инвестиций в основной капитал (в постоянных ценах, в процентах к предыдущему году);

    10. ввод в действие жилых домов на 1000 человек населения (квадратных метров общей площади);

    11. удельный вес домохозяйств, имевших персональный компьютер с доступом к сети Интернет;

    12. индекс потребительских цен (декабрь к декабрю предыдущего года, в процентах)

    13. мощность амбулаторно-поликлинических учреждений на 10000 человек населения (на конец года, тысяч посещений в смену);

    14. среднемесячная номинальная начисленная заработная плата работников организаций (рублей).

    Можно предположить, что каждый из перечисленных показателей в той или иной мере влияет на значение уровня безработицы в Российской Федерации. Так, удельный вес убыточных организаций может влиять с той точки зрения, что обычно в связи с неблагоприятным экономическим положением на фирме часть работников вынуждены ее покинуть и начать искать себе новое место работы. Демографические факторы также могут повлиять на уровень безработицы, так как при увеличении численности людей или мигрантов увеличивается конкуренция на рынке труда. Такой показатель, как удельный вес домохозяйств, имевших персональный компьютер с доступом к сети Интернет должен коррелировать с зависимой переменной, так как в современном мире общение между работодателем и потенциальным работником осуществляется именно в Интернете. Более того, глобальная сеть помогает контактировать тем участникам на рынке труда, которые могут находиться друг от друга в тысячах километров.

    3.1.1. Корреляционно-регрессионный анализ


    Регрессионный анализ - есть метод исследования зависимости результативного признака у (случайной величины) от нескольких случайных величин х1,х2,…,хk, называемых факторами или регрессорами. Исследование причинно-следственной связи между показателями является одной из основных задач общей теории статистики.

    Одной из предпосылок регрессионного анализа является нормальность распределения изучаемых факторов и, главным образом, результирующей переменной. Также, изучаемые единицы должны быть качественно однородными. С целью приведения всех признаков к одинаковым единицам обычно используют принцип нормировки, то есть каждую центрированную величину признака делят на среднее квадратическое отклонение: 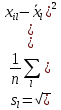, где – значение l-го признака у j-го объекта, - среднее арифметическое значение l-го признака, а – среднее квадратическое отклонение.

    После того как все признаки были нормированы, мы проверяем зависимую переменную «уровень безработицы» на нормальность её распределения по правилу 3-х сигм. Данное правило является частным случаем при рассмотрении закона о нормальном распределении и формулируется следующим образом: вероятность отклонения случайной величины от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение (сигма), стремится к нулю. Таким образом, после применения данного правила к результирующей переменной с целью приведения распределения к нормальному виду были удалены из рассмотрения республика Калмыкия, республика Ингушетия, республика Тыва и Чеченская республика, так как уровень безработицы там в несколько раз превосходит соответствующий уровень в оставшихся регионах. В результате, количество наблюдений у нас равно 80.

    Далее производится проверка всех факторов на нормальный закон распределения (приложение 1), используя одновыборочный критерий Колмогорова-Смирнова. Мы проверяем гипотезу о том, что каждая переменная является нормально распределённой на уровне значимости α=0,05, при конкурирующей гипотезе ( не принадлежит нормальному закону распределения).
    Таблица 1

    Одновыборочный критерий Колмогорова-Смирнова
    y
    x1
    x2
    x3
    x4
    x5
    x6
    x7
    x8
    x9
    x10
    x11
    x12
    x13
    x14

    N
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80
    80

    Сред.
    0,00
    0,00
    0,00
    0,00
    0,02
    0,00
    0,02
    0,02
    0,03
    0,03
    0,02
    0,02
    0,00
    0,00
    0,00

    Стд. Откл.
    1,01
    1,01
    1,01
    1,01
    0,99
    1,01
    0,99
    0,99
    0,99
    0,99
    0,99
    0,99
    1,01
    1,01
    1,01

    Статистика Z Колмогорова-Смирнова
    0,74
    1,34
    0,98
    0,80
    1,00
    0,85
    1,00
    0,73
    0,65
    0,91
    0,98
    0,48
    0,92
    1,15
    1,96

    Асимпт. знч. (двухсторонняя)
    0,64
    0,06
    0,30
    0,55
    0,27
    0,46
    0,27
    0,66
    0,80
    0,38
    0,29
    0,98
    0,36
    0,14
    0,00


    На основании получившихся значений, можно сделать вывод о том, что гипотеза о принадлежности каждой переменной нормальному закону распределения не отвергается на уровне значимости α=0,05, за исключением . Т.е. переменные – нормально распределённые величины. Таким образом, предпосылка регрессионного анализа о нормальности распределения показателей выполняется, и мы можем переходить к следующему этапу исследования ( мы также включим пока в анализ ввиду предположения о влиянии размера среднемесячной заработной платы в регионе на уровень безработицы).

    Перед тем как воспользоваться методом регрессионного анализа необходимо выяснить, какие факторы из вышеперечисленных было бы целесообразнее всего использовать для включения в модель. Зачастую, включение большего количества показателей в модель не улучшают её статистические свойства, а наоборот ухудшают, ввиду, к примеру, наличия мультиколлинеарности между переменными. Наиболее обоснованным методом для выбора факторов является.

    Корреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков. На данный момент, он определяется как метод, применяемый в случае, когда наблюдение считается случайным и выбранным из генеральной совокупности, распределённой по многомерному нормальному закону распределения. Основной задачей данного анализа является оценка корреляционной матрицы генеральной совокупности по выборке и определении частных и множественных коэффициентов корреляции и детерминации на её основе оценок. Другими словами, корреляционный анализ позволяет обработать статистические данные, с целью измерения тесноты связи между двумя или более переменными.

    Для определения необходимости включения в уравнение множественной регрессии тех или иных факторов, а также для оценки полученного уравнения на соответствие выявленным связям (используя коэффициент детерминации) мы построим матрицу парных коэффициентов корреляции :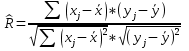

    , где , а .

    Согласно корреляционной матрице (приложение 2), на уровне 0,01 оказались значимыми корреляции между уровнем безработицы и средним временем поиска работы безработными (связь является положительной), удельным весом городского населения в общей численности населения (отрицательная зависимость), коэффициентом пенсионной нагрузки (отрицательная взаимосвязь), общими коэффициентами рождаемости (коэффициент имеет положительный знак), коэффициентами миграционного прироста (отрицательная взаимосвязь), удельным весом домохозяйств, имевших персональный компьютер с доступом к сети Интернет (коэффициент корреляции отрицателен), а также среднемесячная номинальная начисленная заработная плата работников организаций (корреляция является также отрицательной). В то же время, на уровне 0,05 значима связь между уровнем безработицы и такими показателями как индекс потребительских цен и мощность амбулаторно-поликлинических учреждений.

    Надо заметить, что коррелированных между собой показателей достаточно много, однако при этом мультиколлинеарность между факторами не наблюдается. Таким образом, в регрессионную модель могут войти все переменные, кроме показателей удельного веса убыточных организаций (х2), ожидаемой продолжительности жизни при рождении (х6), общих коэффициентов брачности (х7), индекса физического объема инвестиций в основной капитал (х9), ввода в действие жилых домов (х10).

    После проведения корреляционного анализа у нас остались 9 переменных, которые имеют значимую корреляцию на том или ином уровне значимости. Однако включение всех этих факторов в модель может оказаться бессмысленным и увеличение такой характеристики качества построенной модели как коэффициент детерминации может быть результатом добавления в модель большого количества регрессоров. Таким образом, проверим оставшиеся переменные на существенность их включения с помощью дисперсионного анализа.

    Дисперсионный анализ предназначен для проверки зависимостей нормально распределённой случайной величины, являющейся результативным признаком, от нескольких величин – факторных признаков, или факторов, среди которых могут быть как случайные, так и неслучайные величины, измеряемые в любой из шкал: интервальной, порядковой или номинальной4.

    В работе приведён анализ однофакторного комплекса. По очереди изучается влияние 9 факторов на уровень безработицы в Российской Федерации. Исследование существенности влияния каждого фактора на уровень безработицы в РФ заключается в проверке основной гипотезы дисперсионного анализа: уровни факторного признака не влияют на изменение результативной переменной. В данной работе все расчеты производятся на уровне значимости 0,05. Сведем результаты всех расчетов в одну таблицу (приложение 3) и проверим значимость влияния каждого признака в отдельности с помощью F-статистики.

    Таким образом, для переменных х1, х5, х8, х11 и х13 наблюдаемое значение F-статистики превосходит ее критическое значение, т.е. гипотеза о несущественности влияния фактора на изменение результативного признака отвергается с вероятностью ошибки, равной 0,05. Следовательно, можно считать, что следующие переменные существенно влияют на уровень безработицы РФ:

    • среднее время поиска работы безработными (месяцев);

    • общие коэффициенты рождаемости (число родившихся на 1000 человек населения);

    • коэффициенты миграционного прироста на 10000 человек населения;

    • удельный вес домохозяйств, имевших персональный компьютер с доступом к сети Интернет;

    • мощность амбулаторно-поликлинических учреждений на 10000 человек населения (на конец года, тысяч посещений в смену).

    В результате проведенных корреляционного и дисперсионного анализов мы определили, какие переменные далее будут включены в регрессионный анализ, для проверки их статистической значимости. Далее необходимо предоставить дескриптивные статистики для каждой переменной, описать математическую модель зависимости показателей, построить уравнение регрессии, описывающее изменение коррелируемых величин и определяющее среднее значение результативного признака при каком-либо значении факторного.

    Переобозначим все оставшиеся переменные, которые будут использованы в последующем анализе. Так, зависимым признаком будет являться уровень безработицы в РФ (Y), а независимыми – следующие, упомянутые выше показатели:

    1. среднее время поиска работы безработными (месяцев);

    2. общие коэффициенты рождаемости (число родившихся на 1000 человек населения);

    3. коэффициенты миграционного прироста на 10000 человек населения;

    4. удельный вес домохозяйств, имевших персональный компьютер с доступом к сети Интернет;

    5. мощность амбулаторно-поликлинических учреждений на 10000 человек населения (на конец года, тысяч посещений в смену).

    Рассчитаем основные дескриптивные статистики для отобранных переменных и представим результаты в виде следующей таблицы:
    Таблица 2

    Описательные статистики

     
    y
    x1
    x2
    x3
    x4
    x5

    N
    80
    80
    80
    80
    80
    80

    Среднее
    7,18
    8,04
    12,69
    0,64
    48,11
    265,07

    Медиана
    6,95
    7,85
    12,40
    -1,50
    48,15
    257,75

    Стд. отклонение
    2,22
    1,07
    2,28
    61,24
    11,68
    51,47

    Минимум
    1,40
    6,10
    8,60
    -121,00
    13,60
    113,90

    Максимум
    14,20
    12,10
    22,70
    160,00
    75,60
    495,60


    В среднем, уровень безработицы в России по 80 регионам составляет по данным 2011 года 7,18%. При этом, в 40 регионах уровень безработицы держится ниже уровня 6,95%, что является относительно низким показателям в сравнении с имеющимися в предшествующих годах. Самая низкая безработица наблюдается в г. Москве, что, возможно, связано с тем, что в столицу люди приезжают именно с целью поиска работы и готовы принять наименее выгодные предложения ввиду необходимости денежных средств.

    В России, среднее время поиска работы в 2011 году в среднем было чуть более 8 месяцев, при этом стандартное отклонение составляет всего 1 месяц. Таким образом, этот фактор является наиболее однородным, чего нельзя сказать о коэффициенте миграции. В данном случае отток населения из региона приблизительно равен притоку – среднее значение коэффициента составило всего 0,64. При этом, средний коэффициент рождаемости составил 12,69 родившихся на 1000 человек, что говорит об увеличении численности населения внутри самих регионов. Однако, чтобы оценить естественный прирост необходимо рассмотреть значения коэффициентов смертности.

    Среднее и медианное значения удельного веса домохозяйств, имеющих компьютер с выходом в Интернет составили в 2011 году 48%, что говорит о том, что половина населения имеет возможность искать и иметь удаленную работу, что вероятнее всего положительным образом сказывается на общем уровне безработицы. Лучше всего информационно оснащен г. Санкт-Петербург, а после него идет г. Москва, что является достаточно логичным, так как данные регионы считаются наиболее экономически развитыми. Всего 13,6% населения имеют выход в Интернет в республике Дагестан, что связано, скорее всего, с их текущим экономико-политическим положением в регионе.

    Описав все факторы можно переходить к непосредственному построению математической модели. Следует еще раз заметить, что для анализа мы используем нормированные величины каждой переменной, чтобы уменьшить вариацию каждого признака и сделать их более однородными (привести к одной размерности).

    Существует несколько видов уравнений регрессии. В рамках данной работы мы будем анализировать множественную модель линейной регрессии ввиду её простоты и ясности интерпретации. Данная модель выглядит следующим образом: , где t – это номер наблюдения в выборке, а j – номер фактора. - является коэффициентом регрессии, который определяет, на сколько изменится результирующий признак у при изменении факторного признака на единицу. Для определения параметров и чаще всего используют метод наименьших квадратов, который основан на том, что теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, что можно представить в виде формулы: .

    Таким образом, используя алгоритм шагового отбора5, мы построили следующую линейную модель регрессии:







    Проверка на значимость данного уравнения регрессии, используя F-статистику, а также проверка за значимость отдельных его коэффициентов с помощью t-статистики показала, что в обоих случаях гипотеза о незначимости отвергается на уровне . Кроме того, множественный коэффициент детерминации показывает, что данное уравнение регрессии описывает 55,8% вариации результирующего признака вошедшими в модель показателями, а остальная часть вариации обусловлена действием неутонченных факторов.

    Из полученного уравнения следует, что увеличение на одну нормированную единицу общего коэффициента рождаемости (при фиксированных значениях х3 и х4) приводит к увеличению уровня безработицы в среднем на 0,456 (в нормированных единицах). Аналогично, при увеличении на одну нормированную единицу коэффициента миграционного прироста и удельного веса домохозяйств, имеющих компьютер с выходом в Интернет, уровень безработицы снижается в среднем (в нормированных единицах) соответственно на 0,338 (при фиксированных значениях х2 и х4 ) и 0,315 (при фиксированных значениях х2 и х3). Стоит отметить, что также была построена модель с принудительным включением всех переменных, однако согласно статистическим тестам, она оказалась незначимой.

    Для того, чтобы быть уверенным в том, что модель адекватно отражает статистическую связь между показателями, остатки (приложение 5) оцененной регрессии необходимо проверить на нормальность, гомоскедастичность и отсутствие автокорреляции.

    Проверка на нормальность распределения остатков с помощью одновыборочного критерия Колмогорова-Смирнова показала, что с 95% уверенностью мы можем сказать, что остатки являются нормально распределенными (приложение 6).

    Тестирование остатков на гомоскедастичность, что дает нам право полагать об эффективности полученных МНК-оценок и несмещенности и состоятельности оценки ковариационной матрицы этих параметров, основано на предположении о том, что при условии выполнения гипотезы дисперсия ошибок не зависит от значений регрессоров. В данном случае, наблюдаемое значение в рамках теста Бреуша-Пагана-Годфри (приложение 7) не превысило критическое, т.е. гипотеза об отсутствии гетероскедастичности ошибок принимается на уровне значимости 0,05.

    В заключение, с помощью теста Дарбина-Уотсона, построенная модель была проверена на наличие автокорреляции остатков первого порядка, наличие чего может привести также к неэффективности МНК-оценок и к завышению тестовых статистик, по которым проверяется качество модели. Рассчитанная статистика данного теста показала, что нулевая гипотеза Н0 о незначимости коэффициента авторегрессии принимается на уровне значимости .

    В результате корреляционно-регрессионного анализа данных за 2011 год мы получили статистически значимую и адекватную модель. Согласно данной модели уровень безработицы положительно зависит от общего коэффициента рождаемости и отрицательно от коэффициента миграции и удельного веса домохозяйств, имеющих персональный компьютер с выходом в Интернет.

    Положительную зависимость уровня безработицы от числа родившихся на 1000 человек населения (что имеет наибольшее влияние на результирующую переменную при прочих равных) можно объяснить с нескольких точек зрения. Во-первых, растет число человек в регионе, а новые рабочие места не открываются. Более того, в течение последнего десятилетия стали закрываться большие промышленные организации, которые зачастую предоставляли вакантные места для целых городов или поселений. Однако это скорее оказывает влияние в долгосрочной перспективе. С другой стороны, увеличивается число рождений, а следовательно, женщин, оставивших в связи с родами и последующим уходом за грудным ребёнком свое прежнее место работы. По прошествии некоторого времени, эти женщины начинают обращаться в биржи труда с целью поиска работы, тем самым увеличивая уровень безработицы в регионе.

    Отрицательная зависимость между уровнем безработицы и коэффициентом миграционного прироста в регионе, то есть при положительном приросте миграции уровень безработицы сокращается, связана с тем, что миграция зачастую связана именно с работой. Другими словами, те люди, которые меняют свое место жительство, часто мигрируют туда, где либо они уже нашли место работы, либо туда, где они намерены устроиться на неё. Таким образом, в регионе уровень безработицы снижается за счет увеличения рабочей силы в общем и числа занятых в частности.

    Наличие значимой обратной зависимости между уровнем безработицы и долей домохозяйств, имеющих персональный компьютер с выходом в Интернет, подтверждает выдвинутое в начале анализа предположение о том, что данный фактор оказывает влияние на результирующий показатель. Во-первых, это связано с тем, что, как уже было описано выше, Интернет позволяет «стереть» километры между потенциальным работником и работодателем, например, имея возможность работать над проектами удаленно. Во-вторых, глобальная сеть помогает найти работу, минуя биржу труда, контактируя с работодателем напрямую, тем самым позволяя найти работу, на устраиваемых безработного условиях.

    3.1.2. Компонентный анализ


    Стремление описать экономическое явление всегда приводит к рассмотрению большого количества исходных переменных, что в итоге вытекает к ненаглядной модели, оценки которой являются неэффективными. В данном случае сначала были выдвинуты к рассмотрению четырнадцать переменных, которые на первый взгляд оказывают влияние на уровень безработицы. Однако, в ходе корреляционно-регрессионного анализа мы получили модель, в которую вошли три переменные из предположенных в начале анализа. Но, несмотря на то, что данная модель описывает около 56% вариации результирующего признака, исключение не вошедших в модель переменных могло повлечь за собой потерю информации.

    Для того чтобы построить наглядную модель, исключая незначимые факторы и максимально сохранив информацию и структуру исходных данных применяются такие способы снижения размерности как компонентный анализ. Отличительной особенностью такого анализа является то, что, во-первых, главные компоненты имеют нулевую корреляцию между собой, а во-вторых появляется возможность выявить неявные, непосредственно не измеряемые, но объективно существующие закономерности, которые обусловлены действием как внутренних, так и внешних причин.

    Модель компонентного анализа имеет вид: , где – «вес», факторная нагрузка, v-ой главной компоненты на j-ой переменной; - значение v-ой главной компоненты для i-го наблюдения (объекта), где v=1,2,…,k. Для анализа будут выбраны все 14 факторов, вероятно влияющих неким образом на уровень безработицы. Однако, количество главных компонент, включенных в окончательную модель, будут определены их вкладом в суммарную дисперсию.

    В ходе компонентного анализа получили следующие результаты полной объяснённой дисперсии:
    Таблица 3

    Результаты полной объясненной дисперсии

    Компонента
    Начальные собственные значения

    Итого
    % Дисперсии
    Кумулятивный %

    1
    3,456
    24,685
    24,685

    2
    2,826
    20,183
    44,868

    3
    1,648
    11,771
    56,638

    4
    1,163
    8,304
    64,942

    5
    1,039
    7,421
    72,363

    6
    0,865
    6,176
    78,539

    7
    0,768
    5,489
    84,028

    8
    0,608
    4,340
    88,369

    9
    0,447
    3,191
    91,560

    10
    0,363
    2,593
    94,153

    11
    0,300
    2,146
    96,299

    12
    0,258
    1,841
    98,140

    13
    0,149
    1,062
    99,201

    14
    0,112
    0,799
    100,000


    Считается, что можно ограничиться несколькими первыми главными компонентами, если их суммарная объясненная дисперсия превышает 70%. Как видно из таблицы 3, кумулятивный процент объясненной дисперсии первых пяти компонент составляет 72,4%, что является достаточным для использования их в дальнейшем анализе.

    Одним из недостатков компонентного анализа является достаточно сложная смысловая интерпретация главных компонент. Однако рассмотрим с какими переменными тесно связана каждая из них (приложение 8) и попробуем их проинтерпретировать.

    Первая главная компонента (z1), согласно соответствующей матрице, тесно связана со следующими переменными: среднее время поиска работы безработными, удельный вес городского населения в общей численности населения, ожидаемая продолжительность жизни при рождении, общие коэффициенты брачности на 1000 человек населения, удельный вес домохозяйств, имевших персональный компьютер с доступом к сети Интернет, мощность амбулаторно-поликлинических учреждений на 10000 человек населения и среднемесячная номинальная начисленная заработная плата работников организаций. Таким образом, данная компонента отражает социально-экономическую сторону жизни безработных.

    Вторая главная компонента (z2) имеет тесную связь с коэффициентами пенсионной нагрузки, рождаемости и миграционного прироста. Другими словами, она описывает демографические процессы в регионах.

    Третья (z3) и четвертая (z4) компоненты тесно связаны с вводом в действие жилых домов на 1000 человек населения и с индексом потребительских цен соответственно. Таким образом, их можно проинтерпретировать как обеспеченность жильем и инфляция.

    Последняя, пятая главная компонента (z5) имеет тесную связь с удельным весом убыточных организаций, а также с индексом физического объема инвестиций в основной капитал. Ввиду отношения обеих переменных к организациям данная компонента может быть проинтерпретирована как экономическое положение организаций.

    В продолжение анализа, построим линейное уравнение регрессии на главные компоненты, используя пошаговый метод исключения переменных. В результате оценки имеем следующую модель6:






    Если проверить данное уравнение на значимость с помощью F-cтатистики Фишера и его коэффициенты – с помощью t-критерия Стьюдента, то во всех случаях отвергается гипотеза о незначимости коэффициентов и уравнения в целом на 95%-ом уровне значимости. Незначимой является только константа, значение которой стремится к нулю.

    Остатки данной модели (приложение 10), согласно одновыборочному критерию Колмогорова-Смирнова, являются нормально распределенными. Кроме того, тест Бреуша-Пагана-Годфри на отсутствие гетероскедастичности остатков показал, что остатки гомоскедастичны. В заключение, остатки были проверены на независимость, используя статистику Дарбина-Уотсона, которая указала на отсутствие автокорреляции первого порядка. Таким образом, построенную линейную регрессию на первые две главные компоненты можно считать адекватной.

    Как было уже упомянуто выше, возникают затруднения при интерпретации модели, построенной на главные компоненты. Можно отметить, что при увеличении значения компоненты, характеризующей социально-экономическое положение безработных на 1, нормированное значение уровня безработицы уменьшится на 0,257 единиц. Большее влияние оказывает главная компонента, наиболее тесно связанная с демографическими процессами в регионе: при увеличении соответствующей главной компоненты на 1, нормированный уровень безработицы сокращается на 0,706 единиц.

    Если сравнивать регрессию, построенную на главные компоненты и на три определенных фактора, то вторая оказывается более удачной, с точки зрения простоты и ясности интерпретации. Кроме того, если сравнивать скорректированные коэффициенты детерминации, которые учитывают разное количество регрессоров в уравнениях, то в первом случае (регрессия на компоненты) он составляет 0,547 а во втором 0,540. Другими словами, построение модели, используя главные компоненты в качестве факторов, не улучшило полученных ранее результатов. Более того, этот анализ еще раз подтвердил результаты предыдущей модели, так как вторая компонента содержит факторы x2 и x3 (коэффициенты рождаемости и миграционного прироста), а x4 (удельный вес домохозяйств, имеющих персональный компьютер с доступом в Интернет) входит в состав первой главной компоненты.
    1   2   3   4   5   6   7

    написать администратору сайта