стат анализ. Статанализ и планирование эксперимента. Статистический анализ и планирование эксперимента

Название	Статистический анализ и планирование эксперимента
Анкор	стат анализ
Дата	08.01.2023
Размер	0.49 Mb.
Формат файла
Имя файла	Статанализ и планирование эксперимента.docx
Тип	Отчет #876006
страница	3 из 3

1 2 3

Заключение

________________________________________________________

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ

Реалистичное содержание целевой функции.

В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов X_i) Y принята _______________, е.и.:
Реалистичное содержание (сущность) факторов.

В качестве факторов функции отклика X_i принимаются:
X₁ - _______________________________ е.и;

X₂ - _______________________________ е.и;

Х₃ - _______________________________ е.и.
Уровни варьирования значений факторов.

Минимальные и максимальные значения факторов приняты следующие:

Х₁ min = ________;

X₁ max = ________;

Х₂ min= __________ ,

X₂ max= __________ ;

Х₃ min= _________;

X₃ max= _________.

Среднее значение фактора.

Среднее значение фактора определяется по формуле:

.

X₁₀ = ______________________;

X₂₀ = ______________________^;

X₃₀= ______________________.
Интервалы варьирования фактора.

Интервал варьирования определяется по формуле:
dx₁ = X₁₀ – X_1min = _________________________.

dx₂ = X₂₀ – X_2min = __________________________.

dx₃ = X₃₀ – X₃_min = __________________________.
Корректность определения значений факторов.

Фактор	X₁	X₂	Х3
Минимальное значение, Х_i_min
Максимальное значение, X_i_max
Среднее значение, X_i₀
Интервал варьирования dХ_i

Нормированные значения факторов.

Нормированные значения определяются формулой:

.

Х_н1= _____________________;

Х_н2= _____________________;

Х_н3= _____________________.
Матрица планирования полного факторного эксперимента.

Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.

Номер опыта	Нулевой фактор	Нормированные факторы			Взаимодействия нормированных факторов
	Х_0н	Х_1н	Х_2н	Х_3н	Х₁нХ2н	Х2нХ3н	Х1нХ3н	Х1нХ2нХ3н
1
2
3
4
5
6
7
8

Экспериментальные значения целевой функции.

Номер опыта	Y1	Y2	Y3	Y4	Y5
1
2
3
4
5
6
7
8

Расчет среднего арифметического результатов каждого опыта.

Номер опыта	Y1	Y2	Y3	Y4	Y5	Yср
1
2
3
4
5
6
7
8

Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта).

Дисперсия среднего арифметического определяется формулой: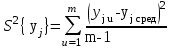

где ?????.

Номер опыта	Y1	Y2	Y3	Y4	Y5	Yср	S²_y
1
2
3
4
5
6
7
8

Оценка однородности построчных дисперсий.

Расчетное значение критерия Кохрена.

Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:

где ?????.
Максимальное значение дисперсии результатов опыта:
S²_ymax= __________ = __________.
Сумма всех построчных дисперсий: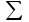

S²_y = ________________________________________________ = _____.
Расчетное значение критерия Кохрена:
Gp= _______.
В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования).

Табличное значение критерия Кохрена.

Уровень значимости.
 = ______.
Степень числителя (f₁):
f1= m –1= ________,
где m – количество параллельных опытов в строке матриц
Степень свободы знаменателя (f2):
f2 = N = ______,
где N – общее число опытов в матрице.
Табличное значение критерия Кохрена
Gт = _________.
Вывод ________________________________________________________
Вид уравнения регрессии, принятого для построения модели функции отклика.

Рекомендуется полиномиальная модель функции отклика
y = ______________________________________________________.
Коэффициенты регрессии.

Значения коэффициентов регрессии определяются по формулам:

;

и так далее для всех коэффициентов.
Таблица - Значения коэффициентов регрессии.

b₀	b₁	b₂	b₃	b₁₂	b₂₃	b₁₃	b₁₂₃

Статистическая значимость коэффициентов регрессии.

Расчетные значения критерия Стьюдента.

Оценка производится по t-критерию Стьюдента. Проверяется отклонение от нуля найденной оценки.

Для каждого коэффициента b_k вычисляется расчетное значение критерия Стьюдента: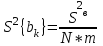

;

,

где b_k – коэффициент уравнения регрессии;

S{b_k} – оценку дисперсию коэффициентов, найденных по экспериментальным данным;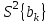

- дисперсия коэффициентов, найденных по экспериментальным данным;

- дисперсия воспроизводимости.
S²_b = _______________________________________ = _____________.
S²_{_bk_}= ___________________ = ______________.
S{bk} = ____________________.
Расчетные значения критерия Стьюдента

t₀	t₁	t₂	t₃	t₁₂	t₂₃	t₁₃	t₁₂₃

Табличные значения критерия Стьюдента.

Уровень статистической значимости.
 = ______________.
Степень свободы
f = _____________.
Функция отклика со статистически значимыми коэффициентами.

Функция отклика со статистически значимыми коэффициентами имеет вид:
y = __________________________
Значения функции отклика для каждого опыта по новой функции отклика со статистически значимыми коэффициентами.

Номер опыта	Y’
1
5
7
3
6
2
4
8

Проверка адекватности новой функции отклика со статистически значимыми коэффициентами.

Расчетное значение критерия Фишера (F- критерия).

Адекватность модели проверяют по критерию Фишера , расчетное значение которого определяется по формуле:

F_p= S²_ад/S²_в ;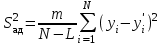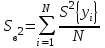

;

,

где ????
S²_ад = ______________ = _________;
S²_в= _______________ = _________;
F_p = _______________ = __________.
Уровень значимости  = ___________.
Степень свободы адекватности:
f_ад = ___________ = ______.
Степень свободы воспроизводимости:
f_в = ___________ = _______.
Табличное значение критерия Фишера.
F_т = ________.
Вывод ________________________________________________________
Функция отклика со статистически значимыми коэффициентами и натуральными факторами.

Функция отклика со статистически значимыми коэффициентами и натуральными факторами имеет вид:
y = ___________.
Заключение _________________________________________________________

Литература

Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399 с.

2.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476 с.
Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с. (электронный ресурс).
Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.
Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983.
Налимов В.В. Теория эксперимента. М.: Наука, 1971.
Планирование и организация измерительного эксперимента / Е.Т. Володаpский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987.

1 2 3