стат анализ. Статанализ и планирование эксперимента. Статистический анализ и планирование эксперимента
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВПО «Иркутский государственный технический университет» Институт недропользования Кафедра Нефтегазового дела СТАТИСТИЧЕСКИЙ АНАЛИЗ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА Макет отчета по контрольной работе для обучающихся по заочно форме обучения Иркутск 2019 г. ВВЕДЕНИЕ Настоящий макет предназначен для помощи обучающимся по программе дисциплины «Статистический анализ и планирование эксперимента» при выполнении контрольной работы. Данный мает применяется следующим образом. Текст макета принимается за основу. В свободные места текста, обозначенные различным образом, необходимо внести результаты выполнения контрольной работы в соответствии с индивидуальным заданием. 1 СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН 1.1. Статистический анализ одномерной последовательности случайных величин Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин. Задание: Подготовить исходные данные. Построить вариационный, статистический, группированный ряды. Построить гистограмму, полигон, кумуляту, огиву. Определить относительные частоты последовательности. Определить: среднее арифметическое (по вариационному ряду), средневзвешенное (по группированному ряду), моду, медиану, дисперсию (по группированному ряду); среднее квадратическое отклонение , коэффициент вариации. Рассчитать в программе Excel характеристики описательной статистики для заданной последовательности случайных величин. Исходные данные В качестве исходных данных принята (назначить самостоятельно числовые характеристики из нефтегазовой сферы или в соответствии с вариантом задания, которые приведены в файле с заданиями) (табл. 1.1). Таблица 1.1- Наименование случайной величины, е.и.
Средствами программы Excel рассчитаны характеристики описательной статистики заданной последовательности значений случайной величины (в качестве исходных данных необходимо применять данные таблицы 1.1), числовые значения которых приведены на рисунке 1.1. 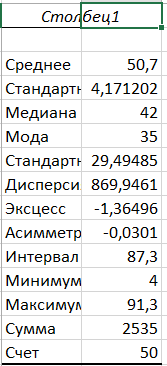 Рисунок 1.1 – Характеристики описательной статистики случайной величины Вариационный ряд Вариационный ряд – последовательность, записанная в возрастающем порядке. Для заданной последовательности случайных величин вариационный ряд показан в таблице 1.2. Таблица 1.2- Вариационный ряд
Характеристики вариационного ряда: максимальное значение ряда Хmax = 91,3; минимальное значение ряда Xmin = 4; размах ряда определяется по формуле: R = Xmax – Xmin = 87,3. Характеристики статистических рядов Статистический ряд - перечень вариант и соответствующих им частот или относительных частот. Могут быть: группированными – например, группируются значения с одинаковыми величинами; интервальными – группировка выполняется по количеству попаданий в интервал (дать определение и классификацию статистических рядов). Группированный статистический ряд Группированный статистический ряд - совокупность середин интервалов (дать определение). Группированный статистический ряд для заданных исходных данных приведен в табл. 1.3. Таблица 1.3 - Группированный статистический ряд
Графическое представление статистических характеристик группированного ряда Гистограмма для группированного ряда. Гистограмма - представляет собой столбиковую диаграмму частот. (дать определение). Гистограмма по заданным значениям группированного ряда показана на рисунке 1.2. 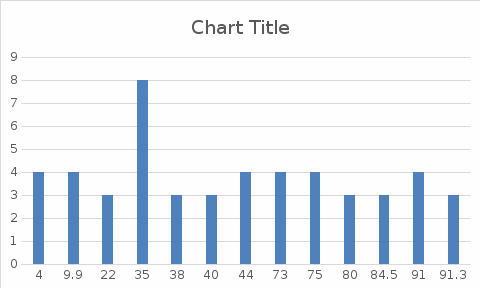 Рисунок 1.2 - Гистограмма для группированного ряда Полигон для группированного ряда Полигон – это ломаная, отрезки которой соединяют середины отрезков, образующих прямоугольники в гистограмме. (дать определение). Полигон для группированного ряда показан на рисунке 1.3. 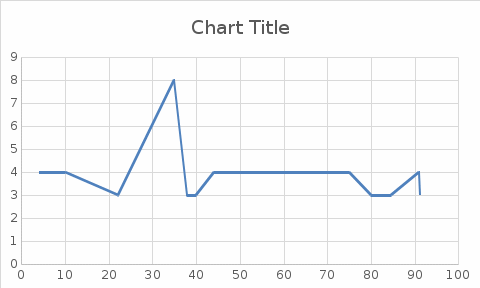 Рисунок 1.3 – Полигон для группированного ряда Кумулята для группированного ряда. Кумулята – служит для графического изображения кумулятивного вариационного ряда. (дать определение). Кумулята для группированного показан на рисунке 1.4. 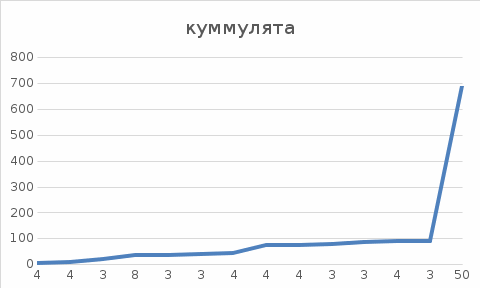 Рисунок 1.4 – Кумулята для группированного ряда Огива для группированного ряда. Огива – это обратная функция по отношению к кумуляте. (дать определение). Огива для группированного ряда показана на рисунке 1.5. 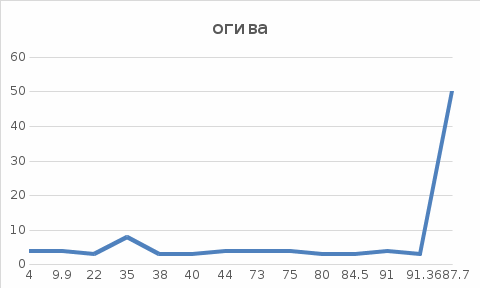 Рисунок 1.5 – Огива для группированного ряда Статистические характеристики группированного ряда Объем выборки группированного ряда. Объем выборки – число случаев, включённых в выборочную совокупность. (дать определение). Объём выборки определяется по формуле: N= (g2 * z2) / d2, где: N – искомый объем выборки; g – дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения; z – коэффициент уровня достоверности (2 – для 0,95, 3 – для 0,99); d – уровень точности. (дать расшифровку всех обозначений в формулах, далее во всех формулах выполнят подобную расшифровку, как это предусмотрено в СТО ИРНИТУ 005-2020 и ГОСТ). При заданных значениях ряда получим: N= ___________________________.= _________, Относительная частота. Относительна частота - (дать определение). Относительна частота определяется по формуле: W =  , ,где N – объе; ni (расшифровать). Для первого значения ряда получим: W = 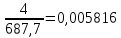 , ,Значения относительных частот приведены в таблице 1.4. Таблица 1.4- Относительные частоты для группированного ряда
Среднее арифметическое группированного ряда. Среднее арифметическое ряда - (дать определение). Среднее арифметическое ряда определяется по формуле: Xср= __________, где ??? Для заданных исходных данных получим: Xсв= ___________. Средневзвешенное группированного ряда. Средневзвешенное значение статистического ряда – (дать определение). Средневзвешенное значение статистического ряда определяется по формуле: X= ________, где ???? Для заданных исходных данных получим: X= ______________________ = _____, Мода группированного ряда Мода – (дать определение). Мода для группированного ряда и для заданного ряда случайных величин имеет значение: M = __________. Медиана группированного ряда. Медианой называется – (определение). Медиана для группированного ряда рассчитывается по формуле: Me = ______ , где ???????. При заданных значениях получим: Me = ______ , Дисперсия группированного ряда. Дисперсия – (дать определение). Дисперсия может быть рассчитана по формуле: D =_________________, где ?????. Данные для расчета дисперсии для других групп ряда приведены в таблице 1.5. Таблица 1.5 – Данные для расчета дисперсии ряда
Тогда дисперсия для группированного ряда определится так: D = ______________________________________________. Среднее квадратическое отклонение группированного ряда. Среднее квадратическое отклонение – (дать определение). Среднее квадратическое отклонение рассчитывается по формуле: σ = 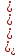 , ,где ????? Для заданных исходных данных получим: σ = ______ = _______. Коэффициент вариации группированного ряда Коэффициент вариации – (дать определение). Коэффициент вариации определяется по формуле: δ = 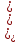 где ??????. Для заданных исходных данных получим: δ = ________= ______. Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда (в качестве исходных данных необходимо применять данные таблицы 1.3), числовые значения которых приведены на рисунке 1.6.  Рисунок 1.6 – Характеристики описательной статистики Вывод. (приводится сравнение расчетных значений, выполненных вручную и выполненной с помощью ПК) ________________________________________________________ Интервальный статистический ряд Интервальный ряд – (дать определение) . Для построения интервального ряда примем количество интервалов t = ______ Ширина интервалов определяется по формуле: rt =__________, где - ??????. При заданных исходных данных получим: rt = ___________. В таблице 1.6 показаны значения границ интервалов и средние значения величин кажого интервала . Таблица 1.6 – Значения границ интервалов
Интервальный ряд представлен в таблице 1.7. Таблица 1.7 - Интервальный ряд
Графическое представление статистических характеристик ряда Гистограмма интервального ряда. Гистограмма по средним значениям интервального ряда показана на рисунке 1.7. Полигон интервального ряда. Полигон для интервального ряда показан на рис. 1.8 Кумулята интервального ряда. Кумулята для интервального ряда показан на рисунке 1.9. Огива интервального ряда. Огива для интервального ряда показана на рисунке 1.10.  Рисунок 1.7 - Гистограмма для интервального ряда  Рисунок 1.8 – Полигон для интервального ряда  Рисунок 1.9 – Кумулята для группированного ряда  Рисунок 1.10 – Огива для интервального ряда Статистические характеристики интервального ряда. Объем выборки интервального ряда. При заданных значениях интервального ряда получим объём выборки: N= ___________________________.= _________, Относительная частота интервального ряда. Для первого значения интервального ряда получим: W = ___________________________.= _________, Значения относительных частот приведены в таблице 1.8. Таблица 1.8- Относительные частоты для группированного ряда
Среднее арифметическое интервального ряда. Для заданных исходных данных получим: Xср= __________________________ = ___________, Средневзвешенное интервального ряда. Для заданных исходных данных получим: Xсв = ______________________ = _____, Мода интервального ряда. Мода для интервального ряда и для заданного ряда случайных величин имеет значение: M = __________. Медиана интервального ряда. Медиана для интервального ряда имеет значение: Me = ______ = ______. Дисперсия интервального ряда. Расчетные значения дисперсии для группированного ряда приведены в таблице 1.9. Таблица 1.9 – Расчет дисперсии ряда
Тогда дисперсия для интервального ряда примет значение: D = ____________________________________. Среднее квадратическое отклонение интервального ряда Для заданных исходных данных получим: σ = ______ = _______. Коэффициент вариации интервального ряда Для заданных исходных данных получим: δ = ________= ______. Характеристики описательной статистики интервального ряда. Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда (для корректного расчета данных характеристик необходимо построить полный интервальный ряд для средних значений случайной величины в табл. 1.10). Таблица 1. 10- Полный интервальный ряд
Числовые значения, рассчитанные в программе Excel, приведены на рисунке 1.11.  Рисунок 1.11 – Характеристики описательной статистики Вывод. (аналогично разделу 3.1) ________________________________________________________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
