Реферат: Вариации интервального ряда числа падения кукурузной муки тонкого помола. Вариации интервального ряда числа падения кукурузной муки тонког. Показатели вариации интервального ряда числа падения кукурузной муки тонкого помола
 Скачать 46.05 Kb. Скачать 46.05 Kb.
|
|
ПОКАЗАТЕЛИ ВАРИАЦИИ ИНТЕРВАЛЬНОГО РЯДА ЧИСЛА ПАДЕНИЯ КУКУРУЗНОЙ МУКИ ТОНКОГО ПОМОЛА Мука кукурузная тонкого помола. Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя)  Мода. Мода ‒ наиболее часто встречающееся значение признака у единиц данной совокупности.  , ,где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота. Выбираем в качестве начала интервала 488, так как именно на этот интервал приходится наибольшее количество. 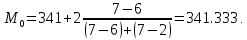 Наиболее часто встречающееся значение ряда – 341.333. Медиана. Медиана делит выборку на две части: половина вариант меньше медианы, половина ‒ больше. Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии «выбросов» данных, медиана более устойчива к воздействию отклоняющихся данных. В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 341-343, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот). 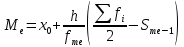 , , Таким образом, 50 % единиц совокупности будут меньше по величине 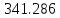 . .В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср = Me = Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср‒Me) ≈ xср‒Mo Квартили. Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25 % единиц совокупности будут меньше по величине Q1, 25 % будут заключены между Q1 и Q2, 25 % ‒ между Q2 и Q3. Остальные 25 % превосходят Q3. 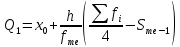 , , Таким образом, 25 % единиц совокупности будут меньше по величине 337.333 Q2 совпадает с медианой, Q2 = 341.286.  , , Остальные 25 % превосходят значение 342.714. Квартильный коэффициент дифференциации. k = Q1 / Q3. k = 337.333 / 342.714 = 0,98. Децили (децентили). Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10 % единиц совокупности будут меньше по величине D1; 80 % будут заключены между D1 и D9; остальные 10 % превосходят D9. 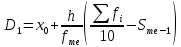 , , Таким образом, 10 % единиц совокупности будут меньше по величине 334.  , , Остальные 10 % превосходят 347. Среднее значение изучаемого признака по способу моментов.  где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой); h – шаг интервала. 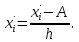 Находим А = 501, шаг интервала h = 26. Средний квадрат отклонений по способу моментов.  Таблица Расчет квадрата отклонений по способу моментов
  Среднее квадратическое отклонение. 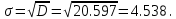 Показатели вариации. Абсолютные показатели вариации. Размах вариации ‒ разность между максимальным и минимальным значениями признака первичного ряда. R = xmax ‒ xmin = 351 ‒ 332 = 19. Среднее линейное отклонение вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.  Каждое значение ряда отличается от другого в среднем на 3.713. Дисперсия характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). 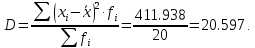 Несмещенная оценка дисперсии ‒ состоятельная оценка дисперсии (исправленная дисперсия).  Среднее квадратическое отклонение. 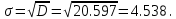 Каждое значение ряда отличается от среднего значения 340.625 в среднем на 4.538. Оценка среднеквадратического отклонения. 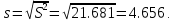 Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации ‒ мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.  Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Линейный коэффициент вариации или Относительное линейное отклонение характеризует долю усредненного значения признака абсолютных отклонений от средней величины. 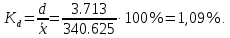 Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней. 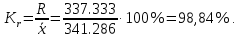 Показатели формы распределения. Относительный показатель квартильной вариации 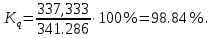 Степень асимметрии. Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии. As = M3/s3, где M3 ‒ центральный момент третьего порядка. s ‒ среднеквадратическое отклонение. M3 = 454.36/100 = 22.72.  Положительная величина указывает на наличие правосторонней асимметрии. Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии: 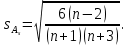 Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Расчет центральных моментов проводим в аналитической таблице. Расчет центральных моментов проводим в аналитической таблице:
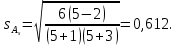 В анализируемом ряду распределения наблюдается несущественная асимметрия (0,243/0,612 = 0,4 < 3). Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона: 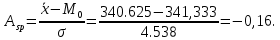 Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: 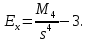 Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) ‒ отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3. M4 = 21579.01/20 = 1078.95. 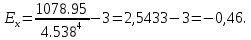 Число 3 вычитается из отношения μ4/σ4 потому, что для нормального закона распределения μ4/σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные ‒ отрицательным эксцессом. Ex < 0 ‒ плосковершинное распределение. Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx, где sEx ‒ средняя квадратическая ошибка коэффициента эксцесса.  Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным. 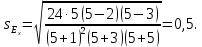 Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным. Интервальное оценивание центра генеральной совокупности. Доверительный интервал для генерального среднего.  Определяем значение tkp по таблице распределения Стьюдента. По таблице Стьюдента находим: Tтабл (n‒1; α/2) = Tтабл (19; 0,025) = 2,433. Стандартная ошибка выборки для среднего: 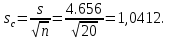 Стандартная ошибка среднего указывает, на сколько среднее выборки 340,625 отличается от среднего генеральной совокупности. Предельная ошибка выборки равна:  или ε = tkp sc = 2,433×1.041 = 2,533. Доверительный интервал: (340.625 - 2.533;340.625 + 2.533) = (338.092;343.158). С вероятностью 0,95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Доверительный интервал для дисперсии. Вероятность выхода за нижнюю границу равна P(X2n-1 < hH) = (1-γ)/2 = (1-0.954)/2 = 0.023. Для количества степеней свободы k = 19 по таблице распределения χ2 находим: X2(19;0.023) = 11.65091. Случайная ошибка дисперсии нижней границы: 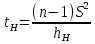  Вероятность выхода за верхнюю границу равна P(X2n-1 ≥ hB) = 1 - P(X2n-1 < hH) = 1 - 0.023 = 0.977. Для количества степеней свободы k = 19, по таблице распределения X2 находим: X2(19;0.977) = 11.65091. Случайная ошибка дисперсии верхней границы: 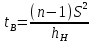 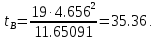 Таким образом, интервал (35.36;35.36) покрывает параметр S2 с надежностью γ = 0.954 Доверительный интервал для среднеквадратического отклонения. S(1-q) < σ < S(1+q) Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 20 По таблице q=q(γ ; n) определяем параметр q(0.954;20) =4.656(1-) < σ < 4.656(1+) 4.656 < σ < 4.656 Таким образом, интервал (4.656;4.656) покрывает параметр σ с надежностью γ = 0.954 Интервальное оценивание генеральной доли (вероятности события). Доверительный интервал для генеральной доли (p· ‒ ε; p· + ε) 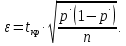 В этом случае 2Ф(tkp) = γ. Ф(tkp) = γ/2 = 0,954/2 = 0,477. По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0,477 tkp(γ) = (0,477) = 2. Таблица Интервальное оценивание генеральной доли
С вероятностью 0,954 при большем объеме выборке эти доли будут находиться в заданных интервалах. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью показателей As и Ex. В случае нормального распределения справедливо следующее условие: |As| < 3SAs; |A| < 3SAs; |E| < 3SEx . Проверим выполнение этого условия для нашего примера. SAs=0.6124, SEx=0.5 As=0.243, Ex=-0.46 |0.243| < 3  0.6124=1.8371 0.6124=1.8371|-0.46| < 3  0.5=1.5 0.5=1.5Условия выполняются. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью правила 3-х сигм. Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал: (x̅ 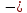 3 · σ; x̅ + 3 · σ) 3 · σ; x̅ + 3 · σ)В нашем случае этот интервал составит: (340.625-3·4.538;340.625-3·4.538) = (327.011;354.239) Все значения величин попадают в интервал, так как xmin=332; xmax=351 Выводы: Каждое значение ряда отличается от среднего значения 340.625 в среднем на 4.538. Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки. Поскольку коэффициент вариации меньше 30%, то совокупность однородна. Полученным результатам можно доверять. Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению. Функция распределения F(X). 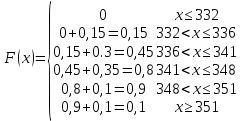 |