Математика. 16.03 7 вариант. По заданном варианту выборочной совокупности независимых и равноточных измерений случайной величины х (св х)

• Название: По заданном варианту выборочной совокупности независимых и равноточных измерений случайной величины х (св х)
• Анкор: Математика
• Дата: 24.03.2022
• Размер: 64.61 Kb.
• Имя файла: 16.03 7 вариант.docx
• Тип: Документы; #414372

По заданном варианту выборочной совокупности независимых и равноточных измерений случайной величины Х (СВ Х).

1. Вычислить точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициента асимметрии.

2. Составить интервальный статический ряд распределения относительных частот и построить гистограмму и полигон относительных частот.

3. Найти эмпирическую функцию распределения и построить ее график.

4. Исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, выдвинуть гипотезу о виде распределения СВ Х, записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками.

5. По критерию согласия 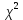Пирсона проверить соответствие выборочного распределения гипотетическому закону для уровня значимости q = 0,05.

6. Вычислить интервальные оценки для математического ожидания m и средеквадратического отклонения, соответствующие доверительным вероятностям γ = 0,95 и γ = 0,99.

Данные о промежутках времени между поступлением заявок в одно из подразделений службы быта в часа представлены в таблице.

4,2 5,3 17,2 15,6 5,9 2,2 4,8 2,2 3,5 0,6

16,1 7,8 13,4 11,2 3,1 7,5 3,8 9,1 0,9 5,1

9,0 8,5 1,2 3,0 0,2 3,5 1,8 1,4 3,5 1,8

13,0 0,5 1,8 7,2 4,2 5,7 1,4 3,2 4,4 3,2

11,3 2,0 8,7 11,8 2,4 8,3 1,7 2,0 1,2 3,2

8,2 0,1 1,4 2,5 3,4 1,8 4,0 1,9 2,5 12,0

5,3 1,2 7,5 5,2 13,0 7,8 20,0 19,0 5,2 6,5

18,0 1,7 9,0 2,3 0,1 3,4 7,5 6,0 3,6 1,6

1,7 3,0 3,2 7,6 10,1 5,5 11,6 3,1 3,8 1,8

7,5 6,4 5,8 3,4 4,2 1,4 7,5 5,2 6,4 7,4

Исключим резко отличающиеся значения:

4,2 5,3 17,2 15,6 5,9 2,2 4,8 2,2 3,5

16,1 7,8 13,4 11,2 3,1 7,5 3,8 9,1 5,1

9,0 8,5 1,2 3,0 3,5 1,8 1,4 3,5 1,8

13,0 1,8 7,2 4,2 5,7 1,4 3,2 4,4 3,2

11,3 2,0 8,7 11,8 2,4 8,3 1,7 2,0 1,2 3,2

8,2 1,4 2,5 3,4 1,8 4,0 1,9 2,5 12,0

5,3 1,2 7,5 5,2 13,0 7,8 5,2 6,5

18,0 1,7 9,0 2,3 3,4 7,5 6,0 3,6 1,6

1,7 3,0 3,2 7,6 10,1 5,5 11,6 3,1 3,8 1,8

7,5 6,4 5,8 3,4 4,2 1,4 7,5 5,2 6,4 7,4

1. Вычислим точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициента асимметрии.

Математическое ожидание:



Точечная оценка дисперсии:



Среднеквадратическое отклонение: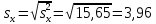



Момент распределения третьего порядка:

М₃ = =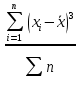

Коэффициент асимметрии: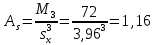



2. Составим интервальный статический ряд распределения относительных частот и построить гистограмму и полигон относительных частот.

Число интервалов:



Ширина интервала:



Интервальный статистический ряд:

Номер интервала	Границы интервала	Число значений	Относительная частота
1	(-∞; 3,3)	33	0,36
2	[3,3; 5,4)	21	0,23
3	[5,4; 7,5)	10	0,11
4	[7,5; 9,6)	15	0,16
5	[9,6; 11,7)	4	0,04
6	[11,7; 13,8)	5	0,05
7	[13,8; 15,9)	1	0,01
8	[15,9; +∞)	3	0,03

Построим гистограмму:



Построим полигон частот: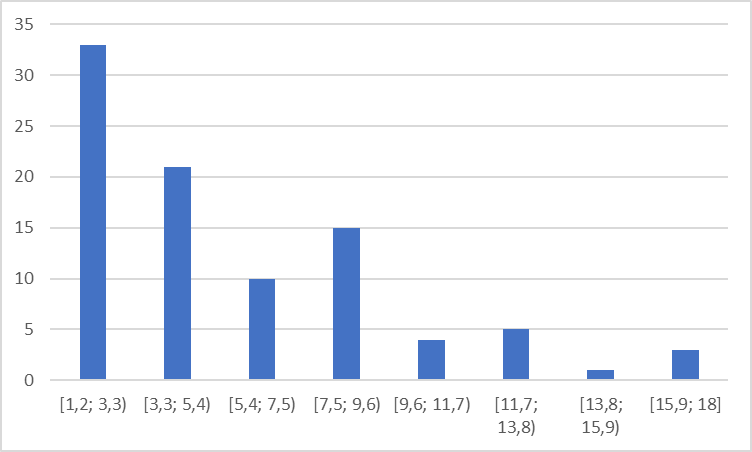



3. Найти эмпирическую функцию распределения и построить ее график.

Запишем значения эмпирической функции распределения в аналитическом виде:



График эмпирической функции распределения:



4. Исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, выдвинуть гипотезу о виде распределения СВ Х, записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками.

Предполагаем нормальный закон распределения.

Плотность распределения вероятностей:



Функция распределения вероятностей:



5. По критерию согласия 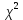Пирсона проверить соответствие выборочного распределения гипотетическому закону для уровня значимости q = 0,05.

По виду гистограммы предполагаем нормальное распределение.

Вычислим теоретические частоты:

Номер интервала	Интервалы	Число значений, ni	P’
1	(-∞; 3,3)	33	0,279	25,63	2,12
2	[3,3; 5,4)	21	0,199	18,29	0,40
3	[5,4; 7,5)	10	0,205	18,83	4,14
4	[7,5; 9,6)	15	0,160	14,74	0,00
5	[9,6; 11,7)	4	0,095	8,76	2,59
6	[11,7; 13,8)	5	0,043	3,96	0,27
7	[13,8; 15,9)	1	0,015	1,36	0,09
8	[15,9; +∞)	3	0,004	0,35	19,80
				Сумма:	29,43

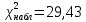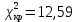Из таблицы получаем наблюдаемое значение критерия Пирсона: . Критическая точка для уровня значимости 5% при количестве степеней свободы k = 8-2= 6 . Так как наблюдаемое значение критерия больше критического значения, то гипотезу о нормальном законе распределения отвергаем.

6. Вычислим интервальные оценки для математического ожидания m и среднеквадратического отклонения, соответствующие доверительным вероятностям γ = 0,95 и γ = 0,99.

При доверительной вероятности γ = 0,95: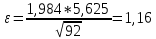



Искомый доверительный интервал для математического ожидания:

5,625 – 1,16 < a < 5,625 + 1,16

4,465 < a < 6,785

По таблице найдем: q (90;0,95) = 0,151

Искомый доверительный интервал для среднеквадратического отклонения: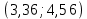





При доверительной вероятности γ = 0,99:



Искомый доверительный интервал для математического ожидания:

5,625 –1,51 < a < 5,625 + 1,51

4,115 < a < 7,135

По таблице найдем: q (90;0,99) = 0,211

Искомый доверительный интервал для среднеквадратического отклонения: