Статистическое исследование результатов ЕГЭ в Москве. Результаты ЕГЭ. Статистический анализ результатов егэ
 Скачать 30.15 Kb. Скачать 30.15 Kb.
|
|
| Год | Округ Москвы | От 160 до 220 | Больше 220 |
| 2017 | Восточный | 2193 | 1643 |
| Западный | 2139 | 1945 | |
| Зеленоградский | 540 | 416 | |
| Новомосковский | 273 | 126 | |
| Северный | 1861 | 1413 | |
| Северо-Восточный | 1857 | 1519 | |
| Северо-Западный | 1457 | 2024 | |
| Троицкий | 182 | 119 | |
| Центральный | 2163 | 3385 | |
| Юго-Восточный | 2021 | 1499 | |
| Юго-Западный | 2456 | 2222 | |
| Южный | 2286 | 1894 | |
| 2018 | Восточный | 2285 | 2093 |
| Западный | 2159 | 2677 | |
| Зеленоградский | 613 | 532 | |
| Новомосковский | 411 | 182 | |
| Северный | 1966 | 1822 | |
| Северо-Восточный | 2171 | 1863 | |
| Северо-Западный | 1514 | 1634 | |
| Троицкий | 224 | 207 | |
| Центральный | 2113 | 3858 | |
| Юго-Восточный | 2233 | 1879 | |
| Юго-Западный | 2582 | 2672 | |
| Южный | 2431 | 2361 | |
| 2019 | Восточный | 2330 | 2150 |
| Западный | 2261 | 2944 | |
| Зеленоградский | 586 | 516 | |
| Новомосковский | 495 | 242 | |
| Северный | 2095 | 1973 | |
| Северо-Восточный | 2062 | 1982 | |
| Северо-Западный | 1567 | 1716 | |
| Троицкий | 263 | 209 | |
| Центральный | 2127 | 4067 | |
| Юго-Восточный | 2252 | 2011 | |
| Юго-Западный | 2544 | 2928 | |
| Южный | 2487 | 2630 | |
| 2020 | Восточный | 2189 | 2195 |
| Западный | 2153 | 2808 | |
| Зеленоградский | 573 | 554 | |
| Новомосковский | 427 | 320 | |
| Северный | 2051 | 2093 | |
| Северо-Восточный | 1994 | 1945 | |
| Северо-Западный | 1562 | 1679 | |
| Троицкий | 222 | 198 | |
| Центральный | 2074 | 4062 | |
| Юго-Восточный | 2076 | 1892 | |
| Юго-Западный | 2406 | 2823 | |
| Южный | 2368 | 2601 | |
| 2021 | Восточный | 2210 | 2315 |
| Западный | 2118 | 2836 | |
| Зеленоградский | 577 | 541 | |
| Новомосковский | 628 | 491 | |
| Северный | 2195 | 2190 | |
| Северо-Восточный | 1981 | 2138 | |
| Северо-Западный | 1625 | 1898 | |
| Троицкий | 175 | 155 | |
| Центральный | 2257 | 4349 | |
| Юго-Восточный | 2080 | 2055 | |
| Юго-Западный | 2400 | 2997 | |
| Южный | 2405 | 2611 |
Таблица 1 – Исходные данные.
Обработанные результаты сведем в таблицу:
| Год | Округ Москвы | 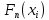 | 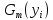 | 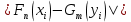 |
| 2017 | Восточный | 0,11287832 | 0,090249931 | 0,022628389 |
| Западный | 0,222977146 | 0,197088712 | 0,025888435 | |
| Зеленоградский | 0,250772082 | 0,219939577 | 0,030832505 | |
| Новомосковский | 0,264823965 | 0,226860753 | 0,037963213 | |
| Северный | 0,360613548 | 0,304476792 | 0,056136755 | |
| Северо-Восточный | 0,456197241 | 0,387915408 | 0,068281833 | |
| Северо-Западный | 0,531192094 | 0,499093656 | 0,032098438 | |
| Троицкий | 0,540560017 | 0,505630321 | 0,034929695 | |
| Центральный | 0,651894173 | 0,69156825 | 0,039674077 | |
| Юго-Восточный | 0,755919292 | 0,773908267 | 0,017988975 | |
| Юго-Западный | 0,882334775 | 0,895962648 | 0,013627873 | |
| Южный | 1 | 1 | 0 | |
| 2018 | Восточный | 0,110375809 | 0,096097337 | 0,014278472 |
| Западный | 0,21466525 | 0,219008264 | 0,004343015 | |
| Зеленоградский | 0,244275915 | 0,243434343 | 0,000841572 | |
| Новомосковский | 0,26412907 | 0,251790634 | 0,012338436 | |
| Северный | 0,35909574 | 0,335445363 | 0,023650377 | |
| Северо-Восточный | 0,463964834 | 0,420982553 | 0,042982282 | |
| Северо-Западный | 0,537097865 | 0,49600551 | 0,041092355 | |
| Троицкий | 0,547918076 | 0,505509642 | 0,042408434 | |
| Центральный | 0,649985509 | 0,682644628 | 0,032659119 | |
| Юго-Восточный | 0,757849483 | 0,768916437 | 0,011066954 | |
| Юго-Западный | 0,882571732 | 0,891597796 | 0,009026064 | |
| Южный | 1 | 1 | 0 | |
| 2019 | Восточный | 0,110589017 | 0,092006162 | 0,018582855 |
| Западный | 0,21790308 | 0,217990414 | 0,00008733 | |
| Зеленоградский | 0,245716455 | 0,240071893 | 0,005644562 | |
| Новомосковский | 0,269210689 | 0,250427936 | 0,018782753 | |
| Северный | 0,368645878 | 0,334859637 | 0,033786241 | |
| Северо-Восточный | 0,466514785 | 0,419676481 | 0,046838304 | |
| Северо-Западный | 0,540889458 | 0,493110236 | 0,047779222 | |
| Троицкий | 0,553372253 | 0,502054091 | 0,051318162 | |
| Центральный | 0,654326261 | 0,676095515 | 0,021769254 | |
| Юго-Восточный | 0,761213157 | 0,762153372 | 0,000940215 | |
| Юго-Западный | 0,881959277 | 0,887452927 | 0,00549365 | |
| Южный | 1 | 1 | 0 | |
| 2020 | Восточный | 0,10893257 | 0,094734571 | 0,014198 |
| Западный | 0,21607365 | 0,215925766 | 0,00008733 | |
| Зеленоградский | 0,244588206 | 0,239835995 | 0,004752211 | |
| Новомосковский | 0,265837273 | 0,253646957 | 0,012190316 | |
| Северный | 0,367902463 | 0,343979284 | 0,02392318 | |
| Северо-Восточный | 0,467131127 | 0,42792404 | 0,039207087 | |
| Северо-Западный | 0,544861906 | 0,500388433 | 0,044473473 | |
| Троицкий | 0,55590943 | 0,508933966 | 0,046975464 | |
| Центральный | 0,659119184 | 0,684246871 | 0,025127687 | |
| Юго-Восточный | 0,762428465 | 0,765904186 | 0,003475722 | |
| Юго-Западный | 0,882159741 | 0,887742771 | 0,00558303 | |
| Южный | 1 | 1 | 0 | |
| 2021 | Восточный | 0,107016609 | 0,094197591 | 0,012819018 |
| Западный | 0,209578229 | 0,209594727 | 0,00008733 | |
| Зеленоградский | 0,237518764 | 0,231608073 | 0,005910691 | |
| Новомосковский | 0,267928914 | 0,251586914 | 0,016342 | |
| Северный | 0,374219166 | 0,340698242 | 0,033520924 | |
| Северо-Восточный | 0,470146724 | 0,427693685 | 0,042453039 | |
| Северо-Западный | 0,548835407 | 0,504923503 | 0,043911905 | |
| Троицкий | 0,557309573 | 0,511230469 | 0,046079105 | |
| Центральный | 0,666602102 | 0,688191732 | 0,02158963 | |
| Юго-Восточный | 0,767323616 | 0,771809896 | 0,00448628 | |
| Юго-Западный | 0,883540749 | 0,893758138 | 0,010217389 | |
| Южный | 1 | 1 | 0 |
Таблица 2 – Обработанные данные
| Год | 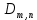 | 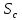 |
| 2017 | 0,068281833 | 6,61957 |
| 2018 | 0,042982282 | 4,42816 |
| 2019 | 0,051318162 | 5,40171 |
| 2020 | 0,046975464 | 4,87315 |
| 2021 | 0,046079105 | 4,88125 |
Таблица 3 – Полученные данные
Численное значение статистики критерия (2) попадет в интервал
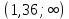 , то есть нулевая гипотеза
, то есть нулевая гипотеза 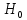 отвергается.
отвергается.Вывод: с помощью критерия однородности Смирнова выяснили, что распределение учеников, набравших выше среднего баллов, по округам не совпадает с распределением учеников, набравших ниже среднего баллов ни в один из годов в промежутке с 2017 по 2021 год.
Список источников:
https://davaiknam.ru/text/lekciya-9-kriterij-kolmogorova-smirnova-proverka-gipotezi-ob-o
https://ami.nstu.ru/headrd/seminar/publik_html/Izm_T_8.htm
http://www.apmath.spbu.ru/ru/staff/kumacheva/files/Tutotial7_Stat1.pdf
https://www.youtube.com/watch?v=cBJTY0JwXm8
https://www.chem21.info/tabs/136028/

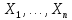 и
и 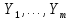 . Данный критерий основан на сравнении эмпирических функций распределения
. Данный критерий основан на сравнении эмпирических функций распределения 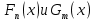 , построенных по первой и второй выборкам соответственно.
, построенных по первой и второй выборкам соответственно.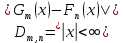 . (1)
. (1)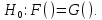 Сформулируем альтернативную гипотезу
Сформулируем альтернативную гипотезу 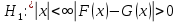 .
. 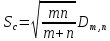 (2)
(2)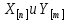 строим эмпирические функции распределения
строим эмпирические функции распределения 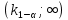 , где
, где 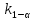 – квантиль уровня 1 – α распределения Колмогорова.
– квантиль уровня 1 – α распределения Колмогорова.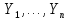 возьмем количество выпускников сдавших экзамен в одном
возьмем количество выпускников сдавших экзамен в одном 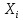 – количество выпускников, получивших общий балл ниже среднего в i-том округе Москвы за 2017 год,
– количество выпускников, получивших общий балл ниже среднего в i-том округе Москвы за 2017 год,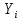 – количество выпускников, получивших общий балл выше среднего в i-том округе Москвы за 2017 год.
– количество выпускников, получивших общий балл выше среднего в i-том округе Москвы за 2017 год.