статистика зо. Статистика Предмет, метод и задачи статистики. Источники статистической информации
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
Статистика 1. Предмет, метод и задачи статистики. Источники статистической информации. Статистика (С) – это вид деятельности, направленной на получение, обработку и анализ информации, характеризующей количественные закономерности жизни общества во всем их многообразии (технико-экономические, социально-политические явления, культура) в неразрывной связи с ее качественным содержанием. Таким образом, под С понимается сбор цифровых данных, их обобщение и обработка. В более узком смысле С рассматривается как совокупность данных о каком-либо явлении или процессе (например, когда говорят о С выборов). Под предметом С понимается количественная сторона массовых общественных явления в постоянной связи с их содержанием или количественной стороной, а также количественное выражение закономерности общественного развития в конкретных условиях места и времени. С опирается на общие положения социально-экономической теории. Вместе с тем у нее свои специфические методы цифрового освещения явления, то есть совокупность приемов, применяемых в процессе статистического исследования. Это наглядно проявляется в том, через какие 3 характерных этапа проходит статистическое исследование: 1) осуществление массового научного организованного наблюдения для получения первичной информации об отдельных единицах явления; 2) группировка и сводка материалов, как распределение всей массы случаев на однородные группы, подсчет характеризующих эти группы количественных показателей и оформление их в виде таблицы; 3) обработка статистических показателей и анализ результатов для получения общих выводов о состоянии явления. В составе С как науки выделяют отделено общую теорию С и производные от нее экономическую С и социальную С. Общая теория С разрабатывает основополагающие принципы и методы статистического исследования общественных явлений, занимается самыми общими категориями С. Экономическая С обеспечивает систематическое количественное описание всех основных сторон экономического процесса и экономики в целом. К ее основным задачам относят: 1) предоставление информации общеэкономического характера органам гос. управления для принятия стратегических решений; 2) предоставление сведений коммерчески значимого характера предпринимателям для правильной организации своей деятельности; 3) информирование общественности страны об актуальных социально-экономических явления. Экономическая С пользуется в России различными источниками данных, все их можно отнести либо к внутренним, которые организует и собирает Федеральная служба государственной статистики (отчетность предприятий, регистр предприятий, переписи и обследования), либо к внешним, организуемые другими ведомствами (административные источники, денежная и банковская статистика, таможенная С и т.д.) 3. Статистическое наблюдение (СН), сводка и группировка. На первом этапе статистического исследования, т.е. на стадии массового научно-организационного наблюдения, решается ключевая задача создания необходимой информационной базы. СН – это систематический научно обоснованный сбор информации о социально-экономических явлениях и процессах. Цель наблюдения определяет объект статистического наблюдения. Под ним понимается определенное явление, которое подлежит наблюдению. Объект статистического наблюдения также есть статистическая совокупность. Под ней понимается множество единиц обладающих некоторыми общими свойствами, существенными для их характеристики СН классифицируется по различным признакам: 1) по охвату единиц совокупности: 1. сплошное (по всем без исключения единицам совокупности); 2. несплошное (например, выборочным); 2) по времени проведения СН бывает: 1) непрерывным (текущим), с систематической регистрацией фактов 2) единовременным (разовое сплошное обследование по мере необходимости) 3) периодическим (например, инвентаризация). На втором этапе статистического исследования прибегают к группировке и сводке. Под группировкой понимается расчленение единиц статистической совокупности на группы, однородные в каком-либо существенном отношении. Признак, по которому единицы совокупности подразделяются на группы именуется группировочным признаком или основанием группировки. Группировка, выполняемая по 1 признаку, называется простой, а по нескольким – комбинированной. Группировочные признаки бывают атрибутивными (в виде текстовой записи) и количественными (имеющими цифровое выражение). После проведения группировки осуществляется обобщение данных наблюдения по выделенным частям и целому по средствам статистической сводки – подсчета числа единиц в подгруппах и группах выделенных при группировке, и подведения количественных итогов. Результаты группировки и сводки оформляются в виде статистических таблиц. В таблице 2 основных элемента: 1. Подлежащее (обычно в первой вертикальной или горизонтальной графе), перечень единиц или групп; 2) сказуемое (цифры, характеризующие эти единицы и группы). Таблицы бывают простыми (части подлежащего не являются группами одинакового качества; групповыми (подлежащее образовано в результате группировки единиц по одному какому-то признаку); комбинационными (подлежащее образовано по двум и более признакам). 7. Абсолютные величины (АВ). Их виды. АВ характеризуют численность совокупности и объем (размер) изучаемого социально-экономического явления в определенных границах времени и места. Они являются всегда именованными числами, т.е. имеют какую-либо единицу измерения. Единицы измерения могут быть натуральные, условно-натуральные, стоимостные (денежные) и трудовые. Выбор единицы измерения зависит от сущности изучаемого явления и конкретных задач исследования. АВ подразделяются на две группы 1. АВ, характеризующие объем явления на определенную дату (например, стоимость основного капитала предприятия на 1 января). Эти величины имеют особенности: если они характеризуют объем явления на определенную дату по нескольким единицам (например, стоимость основного капитала по предприятиям фирмы). То их можно суммировать и получить общий объем явления. Если данные характеризуют объем явления по одной единице на несколько моментов (например, стоимость основного капитала на начало каждого квартала), то эти АВ суммировать нельзя. 2. АВ, характеризующие объем явления за определенный период времени – результат процесса (например, выпуск продукции предприятием за месяц или за год). В это случает позволительно суммировать данные, как за один и тот же период по нескольким единицами, получая общий для них итог, так и за несколько периодов по одной единице, получая итог за боле длительный период. АВ могут быть получены путем суммирования данных статистического наблюдения или расчетным путем. Например, численность населения страны определяется по результатам сводки данных единовременного наблюдения. При определении стоимостных показателей объема продукции АВ получают расчетным путем. 8. Относительные величины (ОВ). Их классификация; основные виды. ОВ получаются в результате сопоставления двух статистических показателей и дают цифровую меру их соотношения. Она получается путем деления сравниваемого показателя на другой показатель, принимаемый за базу сравнения. ОВ подразделяются две группы: 1. ОВ, полученные в результате соотношения одноименных статистических показателей (ОВ динамики, планового задания, выполнения плана, структуры, координации, наглядности) и выражаются или коэффициентом, т.е. показателем того, во сколько раз сравниваемая величина больше или меньше базисной или в процентах; 2) дргие получаются в результате разноименных статистических показателей (так называемые ОВ интенсивности, например, показатель производства продукции на душу населения) и выражаются именованными числами, показывая итог числителя в расчете на 1,10,100 и т.д. единиц знаменателя. ОВ динамики характеризуют изменение явления во времени. Они показывают, во сколько раз увеличился (или уменьшился) объем явления за определенный период времени. ОВ планового задания, выражаются отношением величины показателя по плану к фактической величине показателя в предшествующем периоде. ОВ выполнения плана характеризуется отношением фактической величины показателя в определенном периоде к плановому заданию на тот же период. ОВы структуры (так называемый удельный вес) показывают долю отдельных частей в общем объеме совокупности. ОВы координации выражаются соотношением численности двух частей единого целого, показывая сколько единицы одной группы приходится в среднем на 1, 10, 100 и т.д. единиц другой группы совокупности. ОВы наглядности характеризуются сопоставлением одноименных показателей по одному и тому же моменту или периоду времени, но по разным объекта. Показатель производства продукции на душу населения характеризуется отношением выпуска определенного вида продукции в натуральном выражении за года к среднегодовой численности селения. 9-10. Средние величины (СВ). Средние арифметические. Мода и медиана. Под СВ понимается обобщающий показатель типичного уровня варьирующего количественного признака на единицу совокупности в определенном месте и в определенное время. СВ обязательно является именованной. СВ бывают двух видов: 1) степенные – представляют собой абстрактные характеристики совокупности (средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая); 2) структурные выражаются конкретными величинами, совпадающими в какими-то определенными вариантами совокупности (мода, медиана). Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получивших широкое применение в плановых расчетах, при расчете общей средне из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармоничской определяется характером имеющей в распоряжении исследователя информации. Средняя квадратическая применяется для расчета среднего квадратического отклонения, являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов). Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной.  Структурные средние – мода и медиана – в отличие от степенных выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решения ряда практических задач. Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду). Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака. Для определения медианы сначала определяют ее место в ряду, используя формулу n+1 NMe = -------, где n – число членов ряда. 2 Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую из двух срединных значений. 12. Вариационный ряд (ВР) и его изучение. Построение ряда. Виды рядов. Различия индивидуальных значений признака у единиц совокупности называют вариацией признака. Изучение вариации в переделах однородной группы предполагает использование следующих приемов: построение ВР (ряда распределения); его графическое изображение, исчисление основных характеристик распределения. Построение ВР сводится к созданию групповой таблицы, построенной по количественному признаку, в сказуемом которой показывается число единиц в каждой группе. Тем самым такая таблица фактически представляет собой совокупность сочетания вариантов и соответствующим им частот. Различие индивидуальных значений признака у единицы совокупности называются вариацией признака. По характеру вариации значений признака различают: 1) Признаки с прерывным изменением (дискретные); 2) признаки с непрерывным изменением (непрерывные) Признаки с прерывным изменением могут принимать лишь конечное число определенных значений. Для них применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе – численность единиц с определенным значением признака. Для признака, имеющего непрерывное изменение, строится интервальный ВР, состоящий также как дискретный ряд, из двух граф (варианты и частоты). При его построении в первой графе отдельные значения признака указываются в интервале «от – до», во второй графе – число единицы, входящих в интервал. Интервалы образуются, как правило, равные и закрытые. 16. Выборочное наблюдение (ВН). Основные виды выборки. Наиболее современным и научно обоснованным способом несплошного наблюдения является выборочное наблюдение, получившее в настоящее время широкое применение в работе органов государственной статистики, научно-исследовательских лабораторий, институтов, предприятий. Его использование позволяет лучше организовать наблюдение, обеспечивает быстроту проведения, экономию труда и средств на получение и обработку информации. При ВН обследуется только часть единиц совокупности (ЕС), но таким образом, что эта часть в уменьшенном масштабе представляет всю совокупность. Организация ВН предполагает, прежде всего, правильный отбор исследуемых единиц. По способу организации различают ВН: 1. собственно случайный отбор – производится из всей массы единиц генеральной совокупности, т.е. всей совокупности в целом без предварительного расчленения на какие-либо группы. Принцип случайности обеспечивается жеребьевкой или использованием таблиц случайных чисел. Бывает повторным, когда каждая отобранная единица из генеральной совокупности вновь возвращается в выборку после обследования и может опять попасть в обработку. И бесповторным, когда отобранная единица в выборку не возвращается. 2. механический отбор - наблюдению подвергаются единица, расположенные на равном расстоянии в определенной последовательности среди единиц генеральной совокупности. 3. серийный отбор - в случайном порядке отбираются группы или серии единиц, которые подвергаются сплошному обследованию 4. Комбинированная выборка предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в серии. 5. Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. По степени охвата ЕС различают большие и малые выборки. К безусловно малым относят выборки, объемом мене 30 единиц, и они подлежат исследованию с применением несколько видоизмененных форму. 17. Ошибки выборочного наблюдения. Средняя и предельная ошибки выборки. Все ошибки подразделяются, во-первых, на ошибки регистрации, которые свойственны любому наблюдению (не только выборочному, но и сплошному) и возникают по вине наблюдателя и по вине отвечающего. Во-вторых, на ошибки репрезентативности свойственные только выборочному наблюдению и представляющие собой величину возможных расхождений между показателями выборочной и генеральной совокупностями. Ошибки репрезентативности могут быть систематическими - из-за неправильного, с нарушением научного принципа случайности, отбора единиц. И случайными – зависят от степени однородности совокупности и от объема выборки; возникают даже в том случае, если систематические ошибки репрезентативности устранены. Предельная ошибка рассчитывается по формуле: для средней ∆x=tμx; для доли ∆p=tμp, где t – коэффициент кратности (доверия), а μ – средняя ошибка. Коэффициент кратности по размеру (величине) зависит от заданной вероятности, с которой гарантируется результат и в этой связи берется по специальным таблицам. В экономических расчетах чаще всего используются сочетания: доверительная вероятность р=0,95 t=1,96, р=0,954 t=2,0, р=0,997 t=3,0. Средняя ошибка для:  S2 – выборочная дисперсия (дисперсия признака выборочной совокупности) n – объем выборочной совокупности (число единиц, попавших в выборку) N – объем генеральной совокупности (число единиц, входящих в генеральную совокупность. Кроме того, в рамках выборочного наблюдения можно определять необходимый объем выборки, который с практической вероятностью обеспечивает заданную точность выборки:  . Доверительный интервал и его исчисление. Прежде всего выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней, которая показывает (с определенной вероятностью) на сколько выборочная средняя может отличаться от генеральной средней в большую и меньшую стороны. Тогда величина искомой генеральной средней находится в доверительном интервале: 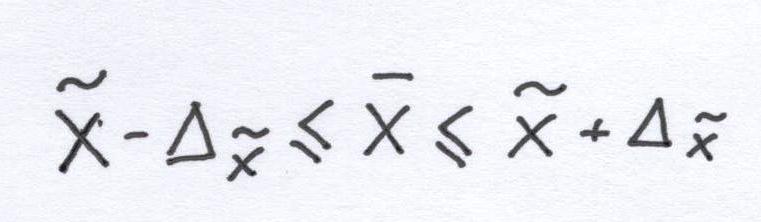 , где , гдех – среднее значение признака выборочной совокупности, ∆x– предельная ошибка средней х – генеральная средняя (среднее значение признака в генеральной совокупности) Аналогичным образом для доли величина генеральной доли находится в доверительном интервале: w-∆р ≤ р ≤ w+∆р w – выборочна доля (доля единиц) ∆р – предельная ошибка доли р - генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности). |
