|
|
Реферат структура данных граф. Структура данных граф
МИНИСТЕРСТВО НАУКИ и высшего образования рф
ФГБОУ ВО «БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Информатика и программное обеспечение»
по дисциплине «Информатика»
Тема «Структура данных граф»
Всего листов_____
Студент гр.О19-ИВТ1-по-Б
зач. кн.№__
______________Ленкевич М.Ю.
\«24\» December 2020 г.
Преподаватель
_________________Зимин С.Н.
\«24\» December 2020 г.
Брянск 2020 г.
Содержание
Содержание 2
Введение 3
Структура данных Граф 4
Определение графа 4
Ориентированный и неориентированный 5
Графы и бинарные отношения 7
Откуда берутся графы 8
Графы и матрицы 9
Взвешенные графы 11
Как реализовать граф 12
Методы обхода графов 14
Поиск в ширину 14
Поиск в глубину 15
Операции над графами 17
Локальные операции 17
Подграфы 18
Алгебраические операции 19
Заключение 22
Список литературы 24
Введение
Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например, задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Структура данных Граф Определение графа
Для описания строения различных систем, состоящих из связанных между собой элементов, часто используют графические схемы, изображая элементы точками (кружками, прямоугольниками и т.д.), а связи между ними – линиями или стрелками, соединяющими элементы. При этом получаются диаграммы вроде тех, что показаны на рис. 1.
На таких диаграммах часто ни способ изображения элементов, ни форма или длина линий не имеют значения – важно лишь, какие именно пары элементов соединены линиями. Если посмотреть внимательно, то можно заметить, что рис. 1.а и 1.б изображают одну и ту же структуру связей между элементами A, B, C, D, E, F. Эту же структуру можно описать, не прибегая к графическому изображению, а просто перечислив пары связанных между собой элементов: (A, B), (A, D), (B, C), (B, E), (B, F), 5 (C, F), (D, E). Таким образом, когда мы отвлекаемся от всех несущественных подробностей, у нас остаются два списка: список элементов и список пар элементов. Вместе они составляют то, что математики называют «графом». Из этого примера видно, что понятие графа само по себе не связано прямо с геометрией или графикой. Тем не менее, возможность нарисовать граф – одна из привлекательных черт этого математического объекта.
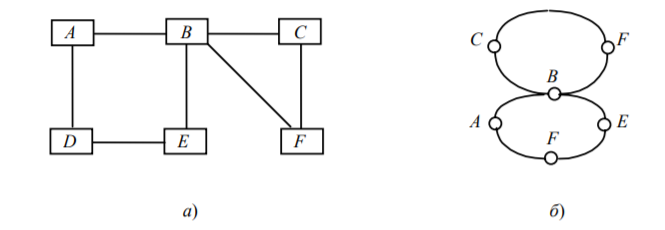
Рис.1
Термин «граф» неоднозначен, это легко обнаружить, сравнивая приводимые в разных книгах определения графа. Однако во всех этих определениях есть и общее. В любом случае граф состоит из двух множеств – множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет. Вершины и ребра называются элементами графа. Здесь будут рассматриваться только конечные графы, то есть такие, у которых оба множества конечны. Чтобы получить законченное определение графа того или иного типа, необходимо уточнить еще следующие три момента.
Ориентированный и неориентированный
Прежде всего, нужно договориться, считаем ли мы пары (a, b) и (b, a) различными. Если да, то говорят, что рассматриваются упорядоченные пары (порядок элементов в паре важен), если нет – неупорядоченные. Если ребро e соединяет вершину a с вершиной b и пара (a, b) считается упорядоченной, то это ребро называется ориентированным, вершина a – его началом, вершина b – концом. Если же эта пара считается неупорядоченной, то ребро называется неориентированным, а обе вершины – его концами. Чаще всего рассматривают графы, в которых все ребра имеют один тип – либо ориентированные, либо неориентированные. В соответствии с этим и весь граф называют ориентированным или неориентированным. На рисунках ориентацию ребра (направление от начала к концу) указывают стрелкой. На рис.1 показаны неориентированные графы, а на рис. 2 – ориентированный.
Кратные ребра
Следующий пункт, требующий уточнения – могут ли разные ребра иметь одинаковые начала и концы? Если да, то говорят, что в графе допускаются кратные ребра. Граф с кратными ребрами называют также мультиграфом. На рис. 2 изображены два графа, левый является ориентированным мультиграфом, а правый – ориентированным графом без кратных ребер.
Петли
Ребро, которому поставлена в соответствие пара вида (a, a), то есть ребро, соединяющее вершину a с нею же самой, называется петлей. Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
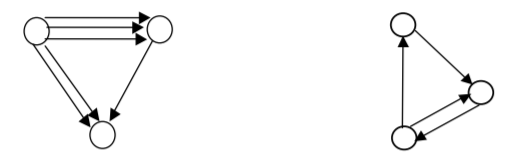
Рис.2
Комбинируя эти три признака, можно получить разные варианты определения понятия графа. Особенно часто встречаются неориентированные графы без петель и кратных ребер. Такие графы называют обыкновенными. Если в графе нет кратных ребер, то можно просто отождествить ребра с соответствующими парами вершин – считать, что ребро это и есть пара вершин. Чтобы исключить петли, достаточно оговорить, что вершины, образующие ребро, должны быть различны. Это приводит к следующему определению обыкновенного графа.
Обыкновенный граф
Обыкновенным графом называется пара G = (V, E), где V – конечное множество, E – множество неупорядоченных пар различных элементов из V. Элементы множества V называются вершинами графа, элементы множества E – его ребрами.
Слегка модифицируя это определение, можно получить определения других типов графов без кратных ребер: если заменить слово «неупорядоченных» словом «упорядоченных», получится определение ориентированного графа без петель, если убрать слово «различных», получится определение графа с петлями. Ориентированный граф часто называют орграфом.
В дальнейшем термин «граф» будем употреблять в смысле «обыкновенный граф», а рассматривая другие типы графов, будем специально это оговаривать.
Множество вершин графа G будем обозначать через VG, множество ребер – EG, число вершин – n(G), число ребер – m(G). Из определения видно, что для задания обыкновенного графа достаточно перечислить его вершины и ребра, причем каждое ребро должно быть парой вершин. Положим, например, VG = {a, b, c, d, e, f }, G = {(a,c), (a,f), (b,c), (c,d), (d,f)}. Тем самым задан граф G с n(G) = 6, m(G) = 5. Если граф не слишком велик, то более наглядным способом представить его является рисунок, на котором вершины изображаются кружками или иными значками, а ребра – линиями, соединяющими вершины. Заданный выше граф G показан на рис. 3. Мы будем часто пользоваться именно этим способом представления графа, при этом обозначения вершин иногда будут помещаться внутри кружков, изображающих вершины, иногда рядом с ними, а иногда, когда имена вершин не существенны, и вовсе опускаться.
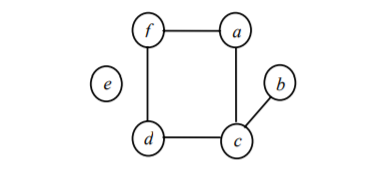
Рис.3
Графы и бинарные отношения
Напомним, что бинарным отношением на множестве A называется любое подмножество R множества A2 , состоящего из всевозможных упорядоченных пар элементов множества A. Каждому такому отношению можно поставить в соответствие граф отношения G = (A, R). Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется рефлексивным, если для любого x ∈ A пара (x, x) принадлежит R, и антирефлексивным, если ни одна такая пара не принадлежит R. Отношение называется симметричным, если из (x, y) ∈ A следует, что (y, x) ∈ R. В графе антирефлексивного и симметричного отношения нет петель и для каждой пары вершин либо нет ни одного, либо есть два ребра, соединяющих эти вершины. Если в таком графе каждую пару ориентированных ребер, соединяющих одни и те же две вершины, заменить одним неориентированным ребром, то получится обыкновенный граф.
Откуда берутся графы
Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы – в этих случаях графы возникают очень естественно и видны «невооруженным глазом». При желании графы можно обнаружить практически где угодно. Яркая демонстрация этого содержится в книге Д. Кнута [D.E.Knuth, The Stanford GraphBase] – графы извлекаются из романа «Анна Каренина», из картины Леонардо да Винчи, из материалов Бюро Экономического Анализа США и из других источников.
Немало поводов для появления графов и в самой математике. Наиболее очевидный пример – любой многогранник в трехмерном пространстве. Вершины и ребра многогранника можно рассматривать как вершины и ребра графа. При этом мы отвлекаемся от того, как расположены элементы многогранника в пространстве, оставляя лишь информацию о том, какие вершины соединены ребрами. На рис. 4 показаны три способа изобразить один и тот же граф трехмерного куба.
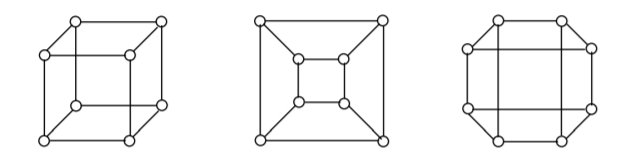
Рис.4
Еще один способ образования графов из геометрических объектов иллюстрирует рис. 5.
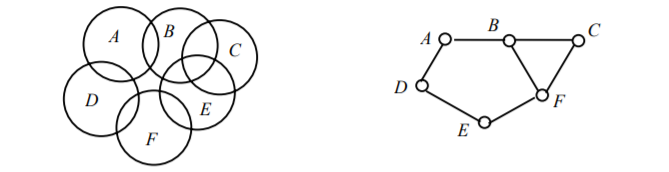
Рис.5
Слева показаны шесть кругов на плоскости, а справа – граф, в котором каждая вершина соответствует одному из этих кругов и две вершины соединены ребром в том и только том случае, когда соответствующие круги пересекаются. Такие графы называют графами пересечений. Можно построить граф пересечений семейства интервалов на прямой, или дуг окружности, или параллелепипедов. Вообще, для любого семейства множеств {S1, …, Sn} можно построить граф пересечений с множеством вершин {1, …, n}, в котором ребро (i, j) имеется тогда и только тогда, когда i ≠ j и Si ∩ Sj ≠ ∅. Известно, что любой граф можно представить как граф пересечений некоторого семейства множеств.
Графы и матрицы
Пусть G – граф с n вершинами, причем VG = {1, 2, …, n}. Построим квадратную матрицу A порядка n, в которой элемент Aij, стоящий на пере11 сечении строки с номером i и столбца с номером j, определяется следующим образом(рис.6)
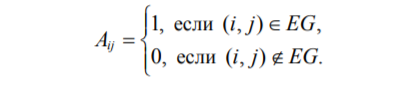
Рис.6
Она называется матрицей смежности графа. Матрицу смежности можно построить и для ориентированного графа, и для неориентированного, и для графа с петлями. Для обыкновенного графа она обладает двумя особенностями: из-за отсутствия петель на главной диагонали стоят нули, а так как граф неориентированный, то матрица симметрична относительно главной диагонали. Обратно, каждой квадратной матрице порядка n, составленной из нулей и единиц и обладающей двумя указанными свойствами, соответствует обыкновенный граф с множеством вершин {1, 2, …, n}.
Другая матрица, ассоциированная с графом – это матрица инцидентности. Для ее построения занумеруем вершины графа числами от 1 до n, а ребра – числами от 1 до m. Матрица инцидентности I имеет n строк и m столбцов, а ее элемент Iij равен 1, если вершина с номером i инцидентна ребру с номером j, в противном случае он равен нулю. На рис. 7 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.
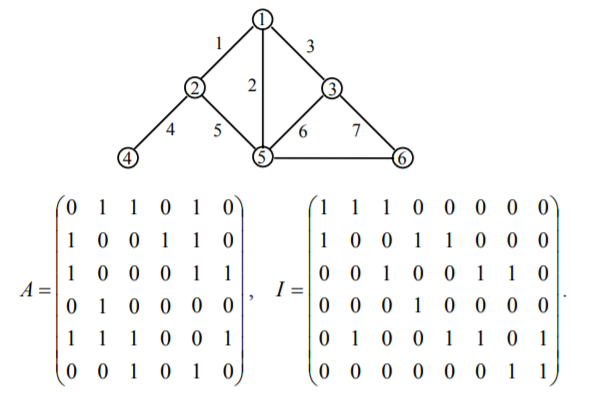
Рис.7
Для ориентированного графа матрица инцидентности определяется несколько иначе: ее элемент Iij равен 1, если вершина i является началом ребра j, он равен –1, если она является концом этого ребра, и он равен 0, если эта вершина и это ребро не инцидентны друг другу.
Взвешенные графы
Часто, особенно когда графы используются для моделирования реальных систем, их вершинам, или ребрам, или и тем и другим приписываются некоторые числа. Природа этих чисел может быть самая разнообразная. Например, если граф представляет собой модель железнодорожной сети, то число, приписанное ребру, может указывать длину перегона между двумя станциями, или наибольший вес состава, который допустим для этого участка пути, или среднее число поездов, проходящих через этот участок в течение суток и т.п. Что бы ни означали эти числа, сложилась традиция называть их весами, а граф с заданными весами вершин и/или ребер – взвешенным графом.
Как реализовать граф
Обыкновенный граф с n вершинами часто представляют матрицей смежности, то есть матрицей размера n × n, в которой элемент, расположенный в i-й строке и j-м столбце, равен 1, если вершины графа с номерами i, j соединены ребром, и равен 0, если такого ребра нет. Если ориентирован, то его матрица смежности симметрична, и можно ограничиться хранением ее треугольной части.
Матричный способ представления может оказаться неэкономным с точки зрения использования памяти, если граф разрежен. Так, например, известно, что число ребер связного планарного графа с n вершинами не превосходит величины (3n − 6) при n ≥ 3, то есть, оценивается величиной O(n), а не как в общем случае O(n2). Представлять такие графы матрицей смежности, как правило, нецелесообразно.
Другой способ представления графа – это список или массив пар вершин, представляющих ребра. При таком способе, если граф не ориентирован, то из двух возможных пар (i, j) и (j, i) целесообразно хранить толь ко одну, например, ту, у которой первая компонента меньше второй.
Еще один способ, часто имеющий преимущества перед указанными выше – это представление графа массивом или списком списков (см. рис. 8). А именно, для каждой вершины организуется список смежных с ней вершин. В этом случае легко осуществляется доступ к окрестностям н. Примерно такого же эффекта можно достичь, представляя граф с помощью двух массивов: inf [1..m] и adr [1..(n + 1)], где m – число ребер графа. Массив adr назовем адресным, а inf – информационным. В информационном массиве вначале перечисляются номера вершин, смежных с первой вершиной, затем со второй и так далее. В адресном массиве указываются номера позиций информационного массива так, чтобы для каждой вершины i по ним можно было находить фрагменты массива inf, в которых записаны номера вершин смежных с этой вершиной. Например, adr[i] может хранить позицию, с которой начинаются в массиве inf вершины, смежные с i-й, при этом adr[n + 1] – первая позиция за пределами массива inf. В таком случае, если нам требуется с каждой вершиной j из окрестности вершины i выполнить оператор S(j), то можно сделать это с помощью оператора цикла(рис.8)
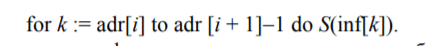
Рис.8
Заметим, что если граф не ориентирован, то каждое ребро (i, j) будет представлено дважды: один раз в последовательности вершин, смежных с вершиной i, а второй раз в последовательности вершин, смежных с вершиной j. Но эта избыточность бывает часто полезна с точки зрения времени выполнения операций над окрестностями вершин графа. Как недостаток такого представления графа можно отметить неудобство при динамической модификации графа, например, добавление к графу ребра может потребовать большого количества пересылок в массиве inf. Этого недостатка лишен способ представления графа, показанный на рис. 9.
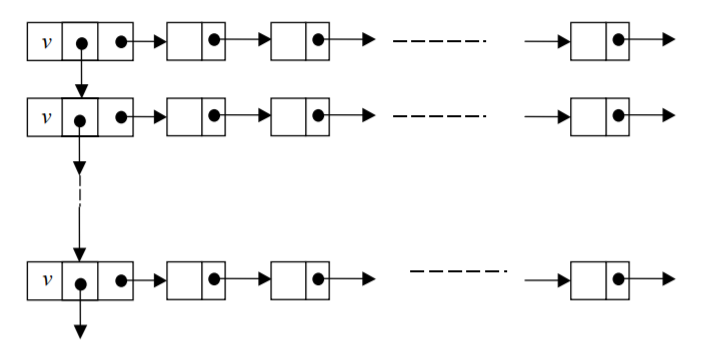
Рис.9
Методы обхода графов
Многие задачи анализа графов могут быть решены путем обхода графа с посещением всех его вершин и исследованием всех его ребер. Такой обход можно выполнить многими способами, в действительности же широкое распространение благодаря своей простоте, а в большей степени благодаря своей полезности, получили две стратегии – поиск в глубину и поиск в ширину. Рассмотрение этих алгоритмов и их применений составляет содержание первых трех разделов настоящей главы. В остальных трех разделах рассматриваются задачи анализа циклов в графах.
Поиск в ширину
Работа всякого алгоритма обхода состоит в последовательном посещении вершин и исследовании ребер. Какие именно действия выполняются при посещении вершины и исследовании ребра – это зависит от конкретной задачи, для решения которой производится обход. В любом случае, однако, факт посещения вершины запоминается, так что с момента посещения и до конца работы алгоритма она считается посещенной. Вершину, которая еще не посещена, будем называть новой. В результате посещения вершина становится открытой и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она превращается в закрытую.
Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их удаленности от некоторой заранее выбранной или указанной стартовой вершины a. Иначе говоря, сначала посещается сама вершина a, затем все вершины, смежные с a, то есть находящиеся от нее на расстоянии 1, затем вершины, находящиеся от a на расстоянии 2, и т.д.
Рассмотрим алгоритм поиска в ширину с заданной стартовой вершиной a. Вначале все вершины помечаются как новые. Первой посещается вершина a, она становится единственной открытой вершиной. В даль42 нейшем каждый очередной шаг начинается с выбора некоторой открытой вершины x. Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине. Если такое ребро соединяет вершину x с новой вершиной y, то вершина y посещается и превращается в открытую. Когда все ребра, инцидентные активной вершине, исследованы, она перестает быть активной и становится закрытой. После этого выбирается новая активная вершина, и описанные действия повторяются. Процесс заканчивается, когда множество открытых вершин становится пустым. Основная особенность поиска в ширину, отличающая его от других способов обхода графов, состоит в том, что в качестве активной вершины выбирается та из открытых, которая была посещена раньше других. Именно этим обеспечивается главное свойство поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена. Для реализации такого правила выбора активной вершины удобно использовать для хранения множества открытых вершин очередь – когда новая вершина становится открытой, она добавляется в конец очереди, а активная выбирается в ее начале. Схематически процесс изменения статуса вершин изображен на рис. 10. Черным кружком показана активная вершина.
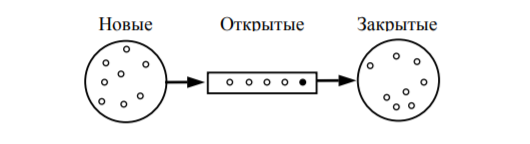
Рис.10
Поиск в глубину
Поиск в глубину – вероятно, наиболее важная ввиду многочисленности приложений стратегия обхода графа. Идея этого метода – идти вперед в неисследованную область, пока это возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые возможности для продвижения вперед. Метод поиска в глубину известен под разными названиями, например, «бэктрекинг», «поиск с возвращением».
Понятия новой, открытой, закрытой и активной вершин для поиска в глубину имеют такой же смысл, как и для поиска в ширину. Отметим, что всегда имеется не более чем одна активная вершина.
Обход начинается с посещения заданной стартовой вершины a, которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине a ребро и посещается вершина y. Она становится открытой и активной. Заметим, что при поиске в ширину вершина a оставалась активной до тех пор, пока не были исследованы все инцидентные ей ребра. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин. Если все ребра, инцидентные активной вершине x, уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер (x, y), это ребро исследуется. Если вершина y новая, то она посещается и превращается в открытую.
Главное отличие от поиска в ширину состоит в том, что при поиске в глубину в качестве активной выбирается та из открытых вершин, которая была посещена последней. Для реализации такого правила выбора наиболее удобной структурой хранения множества открытых вершин является стек: открываемые вершины складываются в стек в том порядке, в каком они открываются, а в качестве активной выбирается последняя вершина. Схематически это показано на рис. 11.
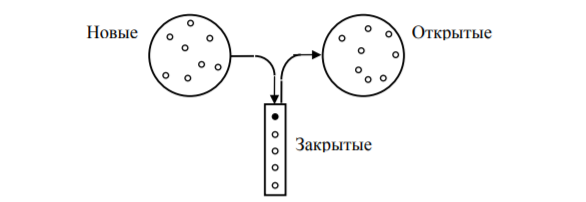
Рис.11
Операции над графами
Для получения новых графов можно использовать разнообразные операции над графами. Здесь мы рассмотрим два вида операций – локальные, при которых заменяются, удаляются или добавляются отдельные элементы графа, и алгебраические, когда новый граф строится по определенным правилам из нескольких имеющихся.
Локальные операции
Простейшая операция – удаление ребра. При удалении ребра сохраняются все вершины графа и все его ребра, кроме удаляемого. Обратная операция – добавление ребра.
При удалении вершины вместе с вершиной удаляются и все инцидентные ей ребра. Граф, получаемый из графа G удалением вершины a, обозначают G – a. При добавлении вершины к графу добавляется новая изолированная вершина. С помощью операций добавления вершин и ребер можно «из ничего», то есть из графа K0, построить любой граф.
Операция стягивания ребра (a, b) определяется следующим образом. Вершины a и b удаляются из графа, к нему добавляется новая вершина c и она соединяется ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин a, b.
Операция подразбиения ребра (a, b) действует следующим образом. Из графа удаляется это ребро, к нему добавляется новая вершина c и два новых ребра (a, c) и (b, c). На рис. 12 изображены исходный граф G, граф G′, полученный из него стягиванием ребра (3, 4) и G″, полученный подразбиением того же ребра. В обоих случаях вновь добавленная вершина обозначена цифрой 7.
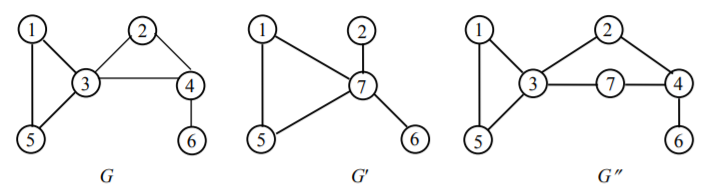
Рис.12
Подграфы
Граф G′ называется подграфом графа G, если VG′ ⊆ VG, EG′ ⊆ EG. Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рис. 13 изображены граф G и его подграфы G1, G2, G3, G4.
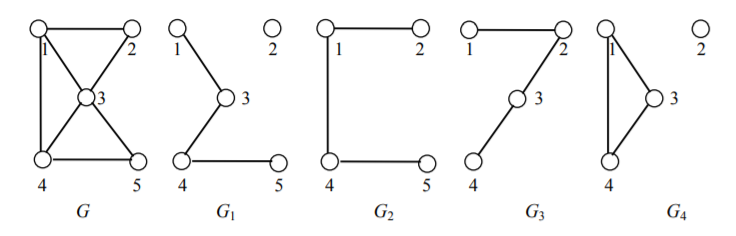
Рис.13
Подграф G′ графа G называется остовным, если VG′ = VG. Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рис. 13 G1 – остовный подграф графа G, а G2, G3 и G4 не являются остовными подграфами.
Другая важная разновидность подграфов – порожденные подграфы. Пусть задан граф G = (V, E) и в нем выбрано множество вершин U ⊆ V. Рассмотрим подграф G′ = (U, E′), где E′ состоит из всех тех ребер графа G, у которых оба конца принадлежат U. Говорят, что этот подграф порожден множеством вершин U. Он обозначается через G〈U 〉. Порожденный подграф может быть получен из графа удалением «лишних» вершин, то есть вершин, не принадлежащих U.
Можно определить также подграф, порожденный множеством ребер F ⊆ E.. Это подграф G′ = (V ′, F), где V ′состоит из всех вершин, инцидентных ребрам из F.
На рис. 13 G2 – подграф графа G, порожденный множеством вершин {1, 2, 4, 5}, то есть G2 = G〈{1, 2, 4, 5}〉, он же порождается множеством ребер {(1,2), (1,4), (4,5)}; подграф G3 не порождается множеством вершин, но порождается множеством ребер {(1,2), (2,3), (3,4)}; подграф G4 не является ни остовным, ни порожденным в каком-либо смысле.
Алгебраические операции
Поскольку граф состоит из двух множеств (вершины и ребра), то различные операции над множествами естественным образом порождают соответствующие операции над графами. Например, объединение двух графов G1 и G2 определяется как граф G = = G1 ∪ G2, у которого VG = VG1 ∪ VG2, EG = EG1 ∪ EG2, а пересечение – как граф G = G1 ∩ G2, у которого VG = VG1 ∩ VG2, EG = EG1 ∩ EG2. Обе операции иллюстрирует рис. 14.
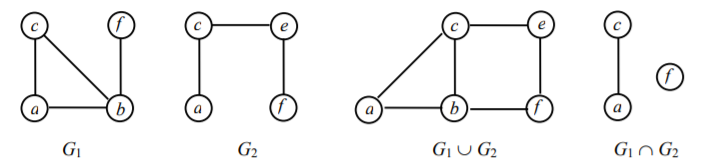
Рис.14
Дополнением (дополнительным графом) к графу G = (V, E) называется граф G, у которого множество вершин то же, что у G, а множество ребер является дополнением множества E до множества всех неупорядоченных пар вершин. Иначе говоря, две различные вершины смежны в графе G тогда и только тогда, когда они не смежны в графе G. Например, On = Kn .
Другой пример показан на рис. 15. Очевидно, всегда G = G.

Рис.15
Под суммой G1 + G2 двух абстрактных графов понимают объединение графов с непересекающимися множествами вершин. Точнее говоря, имеется в виду следующее. Сначала вершинам графов-слагаемых присваиваются имена (пометки, номера) так, чтобы множества вершин не пересекались, затем полученные графы объединяются. Операция сложения ассоциативна, то есть (G1 + G2) + G3 = G1 + (G2 + G3) для любых трех графов. Поэтому можно образовывать сумму любого числа графов, не указывая порядок действий с помощью скобок. Если складываются k экземпляров одного и того же графа G, то полученный граф обозначается через kG. Например, On ≅ nK1. На рис. 1.14 изображен граф C4 + 2K2 + 4K1.
Соединением двух графов G1 и G2 называется граф, получаемый из их суммы добавлением всех ребер, соединяющих вершины первого слагаемого с вершинами второго. Будем записывать эту операцию как G1
ºG2.
Произведение G = G1 × G2 графов G1 и G2 определяется следующим образом. Множеством вершин графа G является декартово произведение множеств VG1 и VG2, то есть вершины этого графа – упорядоченные пары (x, y), где x – вершина первого сомножителя, y – вершина второго. Вершины (x1, y1) и (x2, y2) в G смежны тогда и только тогда, когда x1 = y1 и y1 смежна с y2 в графе G2, или y1 = y2 и x1 смежна с x2 в графе G1. С помощью операции произведения можно выразить некоторые важные графы через простейшие. Например, произведение двух цепей дает прямоугольную решетку – см. рис. 16. Если один из сомножителей превратить в цикл, добавив одно ребро, то прямоугольная решетка превратится в цилиндрическую, а если и второй сомножитель превратить в цикл, то получится тороидальная решетка.
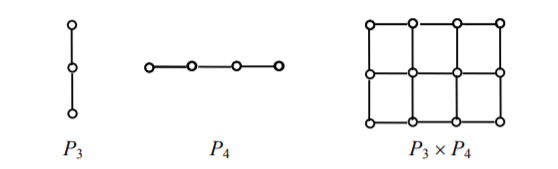
Рис.16
Заключение
Графы имеют очень широкое применение: с их помощью выбирают наиболее выгодное расположение зданий, графами представлены схемы метро. Далее представлены некоторые примеры применения графов.
-Можно составить граф любой позиционной игры: шахмат, шашек, «крестиков – ноликов». Здесь позиции станут вершинами, а направленные отрезки между ними будут означать, что одним ходом можно перейти от одной позиции к другой, по направлению стрелки.
—Лабиринт. Исследовать лабиринт - это найти путь в этом графе. Вершинами здесь обозначены тупики, а отрезками – проходы лабиринта.
—Генеалогическое древо. Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.
Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка – обозначенный ею объект входит в один класс верхнего уровня.
Любая вершина дерева может порождать несколько потомков – вершин, соответствующих классам нижнего уровня.
Для каждой пары вершин дерева существует единственный путь, их соединяющий. Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов.
—Блок схема программы. Графами являются блок – схемы программ для ЭВМ, а так же любые электрические цепи или электрическая сеть.
—Схема цепей дежурного освещения.
Список литературы
1.В.Е. Алексеев, В.А. Таланов. Графы. Модели вычислений. Структуры данных. 2004 г.
2.https://obuchonok.ru/node/1321 |
|
|
 Скачать 391.4 Kb.
Скачать 391.4 Kb.