Практика 5 парам. Практика 5 Парам.сп.. Уравнивание нивелирной сети параметрическим способом Задание
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
|
Уравнивание нивелирной сети параметрическим способом Задание: Уравнять параметрическим способом сеть нивелирования IV класса (рисунок 1). Вычислить уравненные высотные отметки, произвести оценку точности полученных результатов. 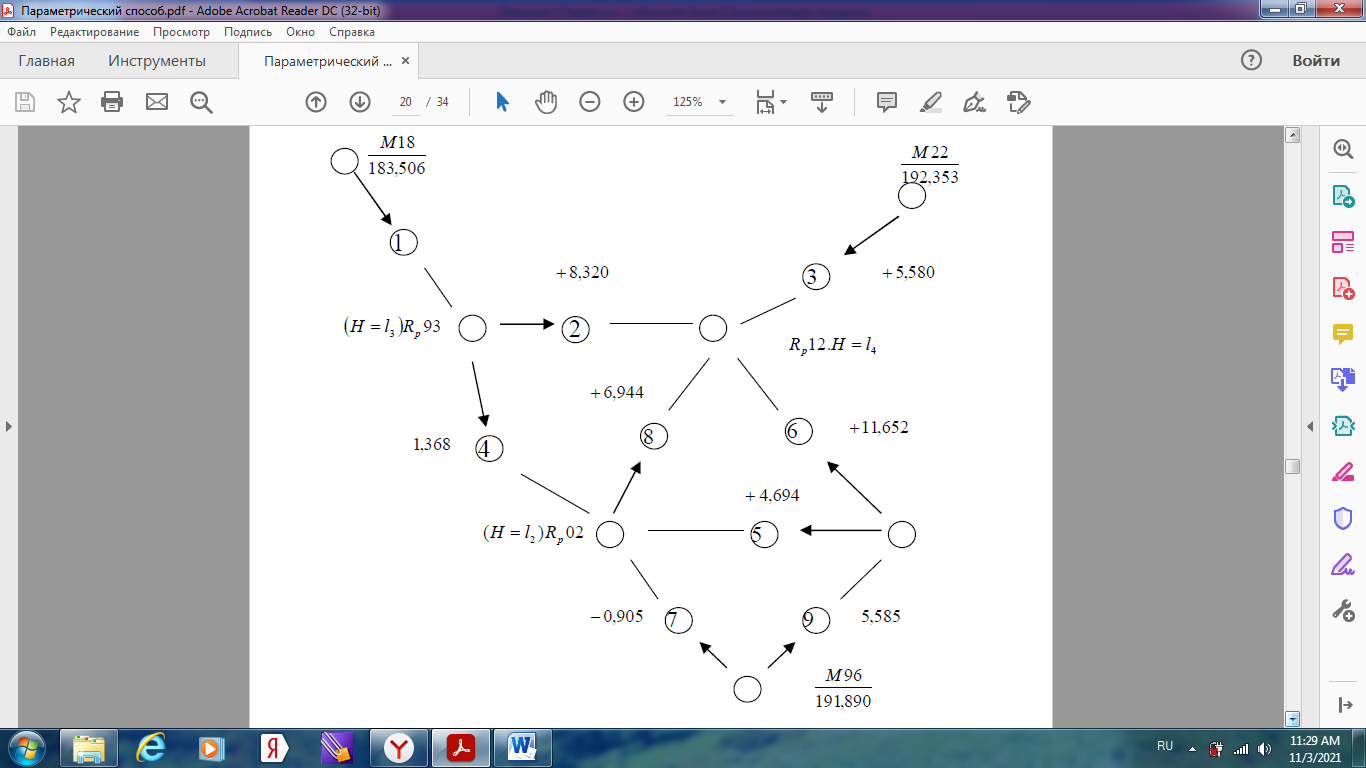 Высоты марок 18, 22 и 96 являются исходными. Высоты реперов 86, 02, 93, 12 –неизвестные. Кружками на рисунке показаны номера звеньев 1, 2 … 9. В качестве измеренных величин примем суммы превышений в звеньях. Их веса можно принимать обратно пропорциональными длинам ходов. Чтобы получить веса, близкие к единице, их вычисляют по формуле Р=15/S Задание: 1) провести уравнения параметрическим способом и получить высоты реперов 86, 02, 93 и 12; 2) получить средние квадратические ошибки: высоты реперов; разностей высот (Н93 – Н86) и (Н12 – Н02); одного километра нивелирного хода. В качестве параметоров выберем необходимые неизвестные в сети, то есть, определяемые высоты: H86 = t1; H02 = t2; H93 = t3; H12 = t4. 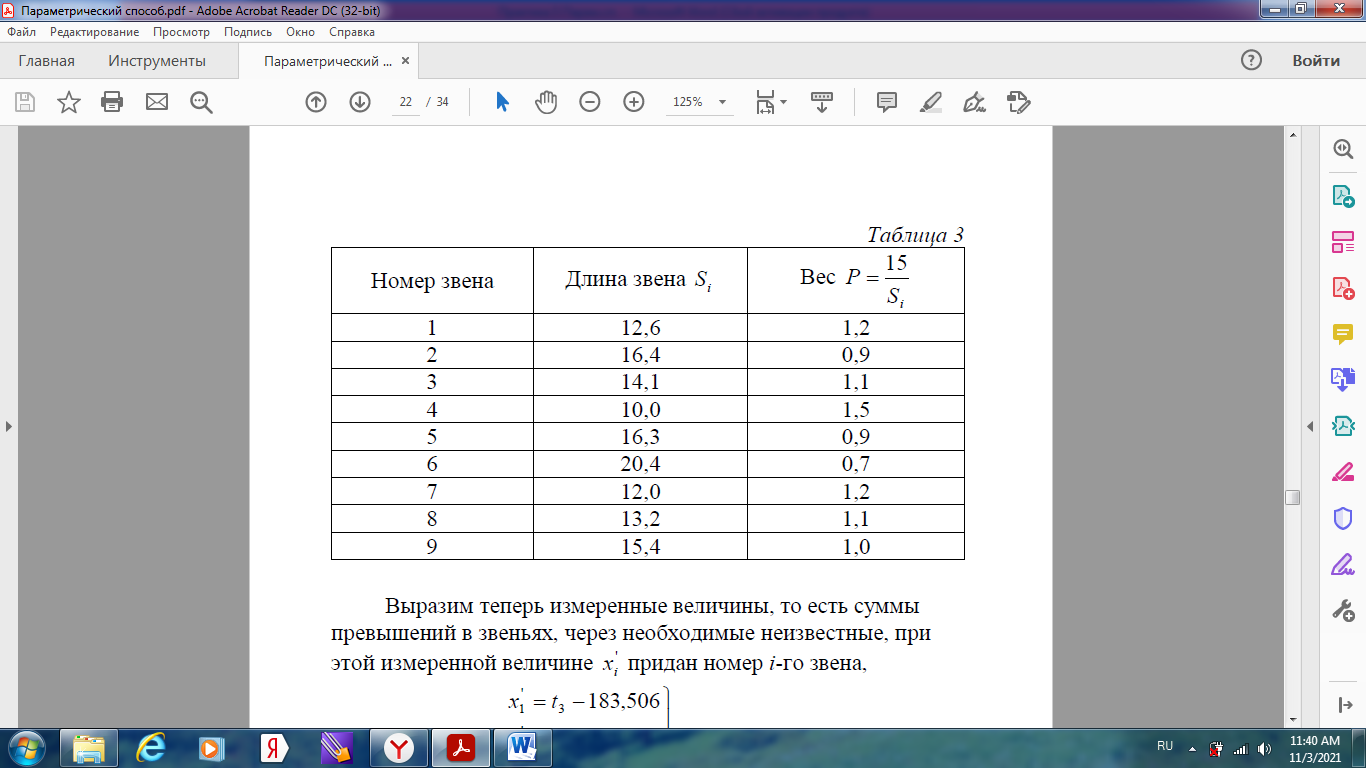 Выразим теперь измеренные величины, то есть суммы превышений в звеньях, через необходимые неизвестные, при этой измеренной величине x i придан номер i-го звена, 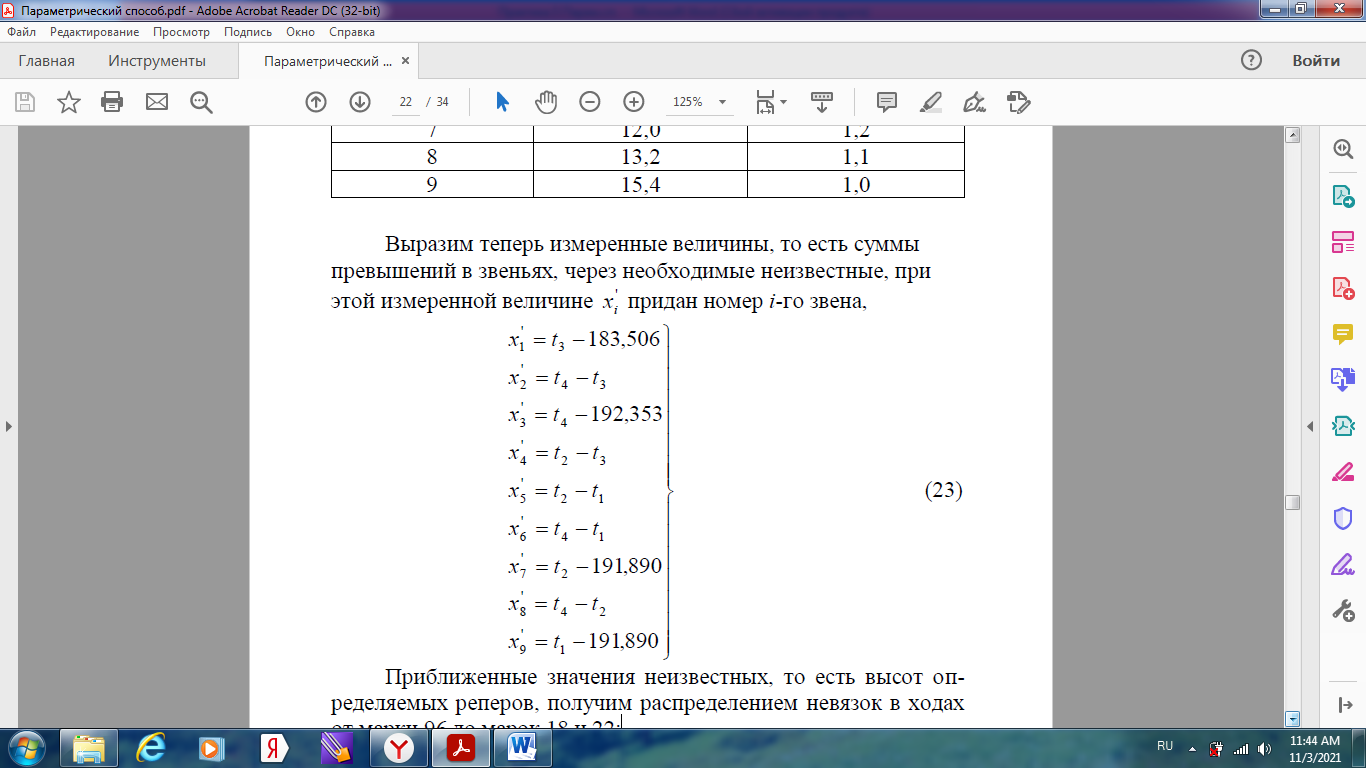 Приближенные значения неизвестных, то есть высот определяемых реперов, получим распределением невязок в ходах от марки 96 до марок 18 и 22: 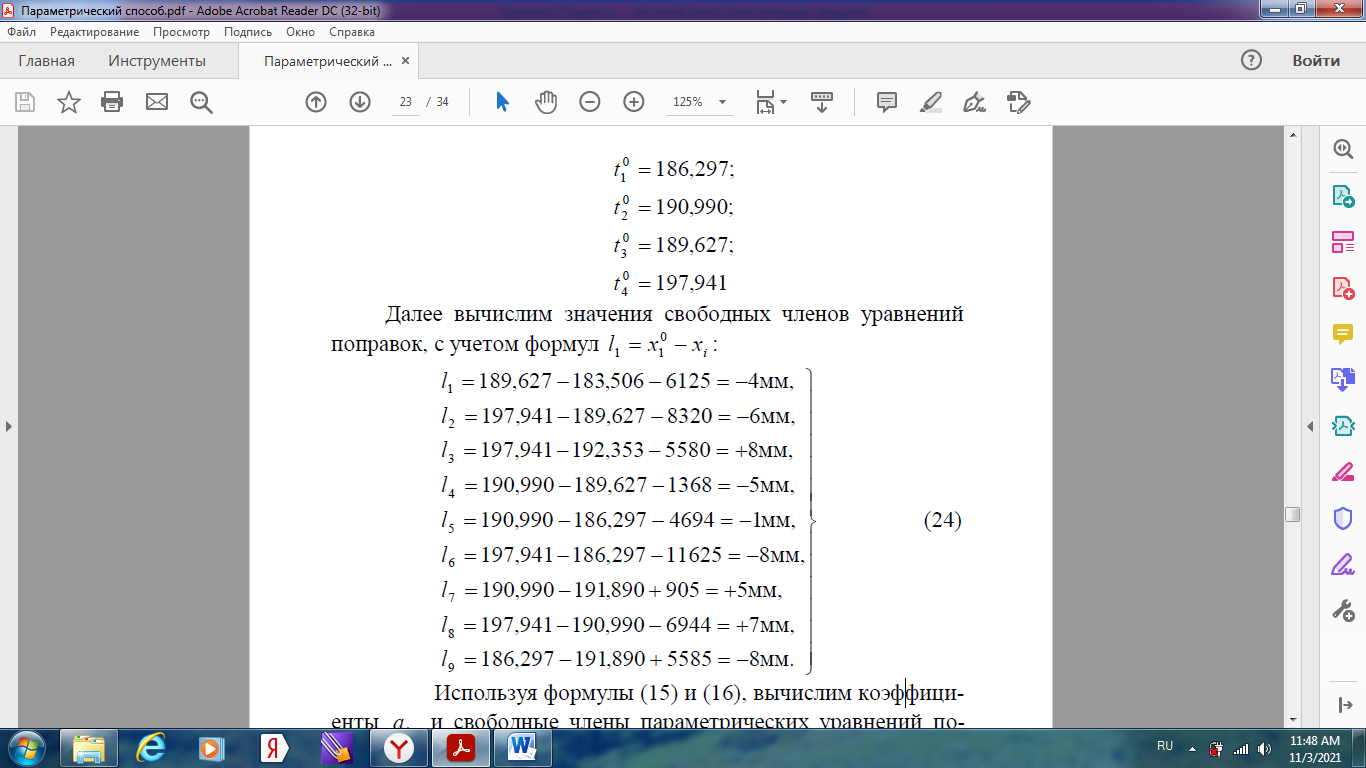 Далее вычислим значения свободных членов уравнений поправок Вычислим коэффициенты aij уравнений поправок: 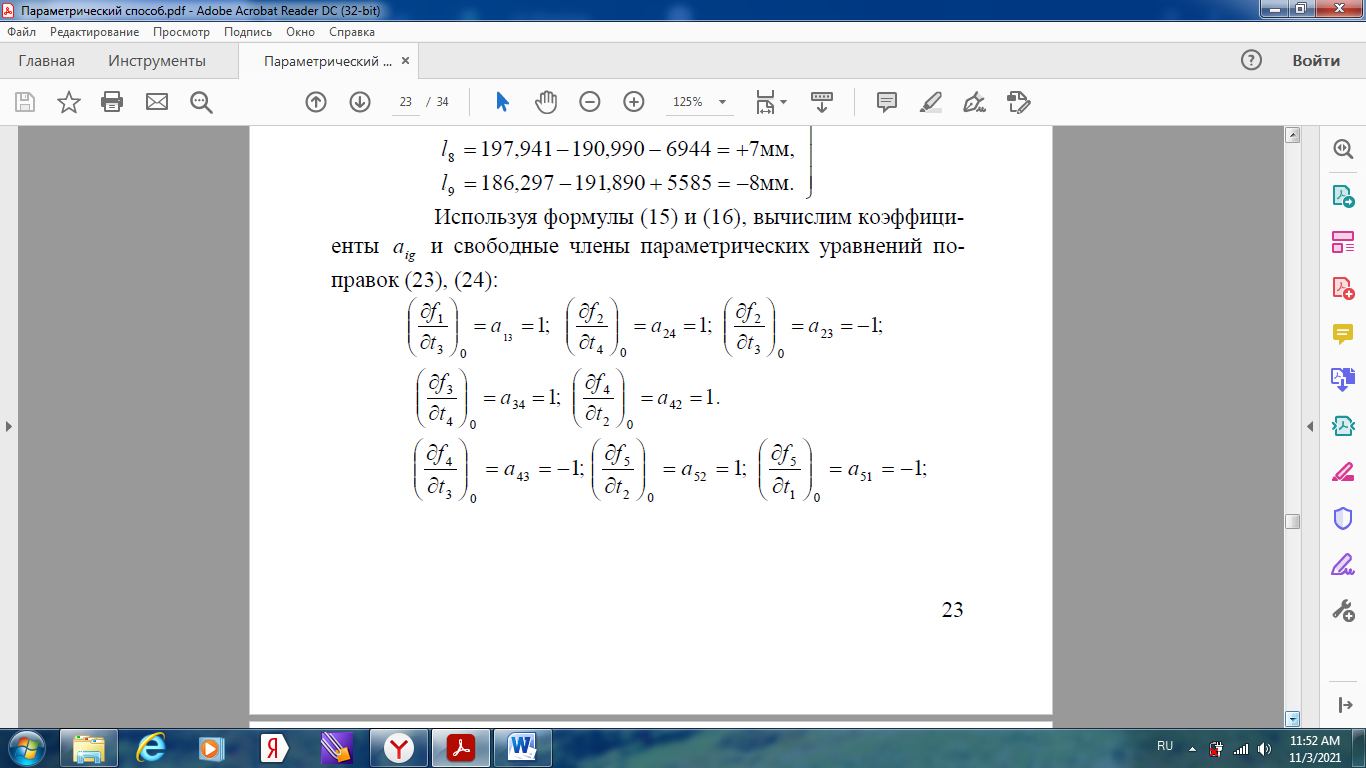 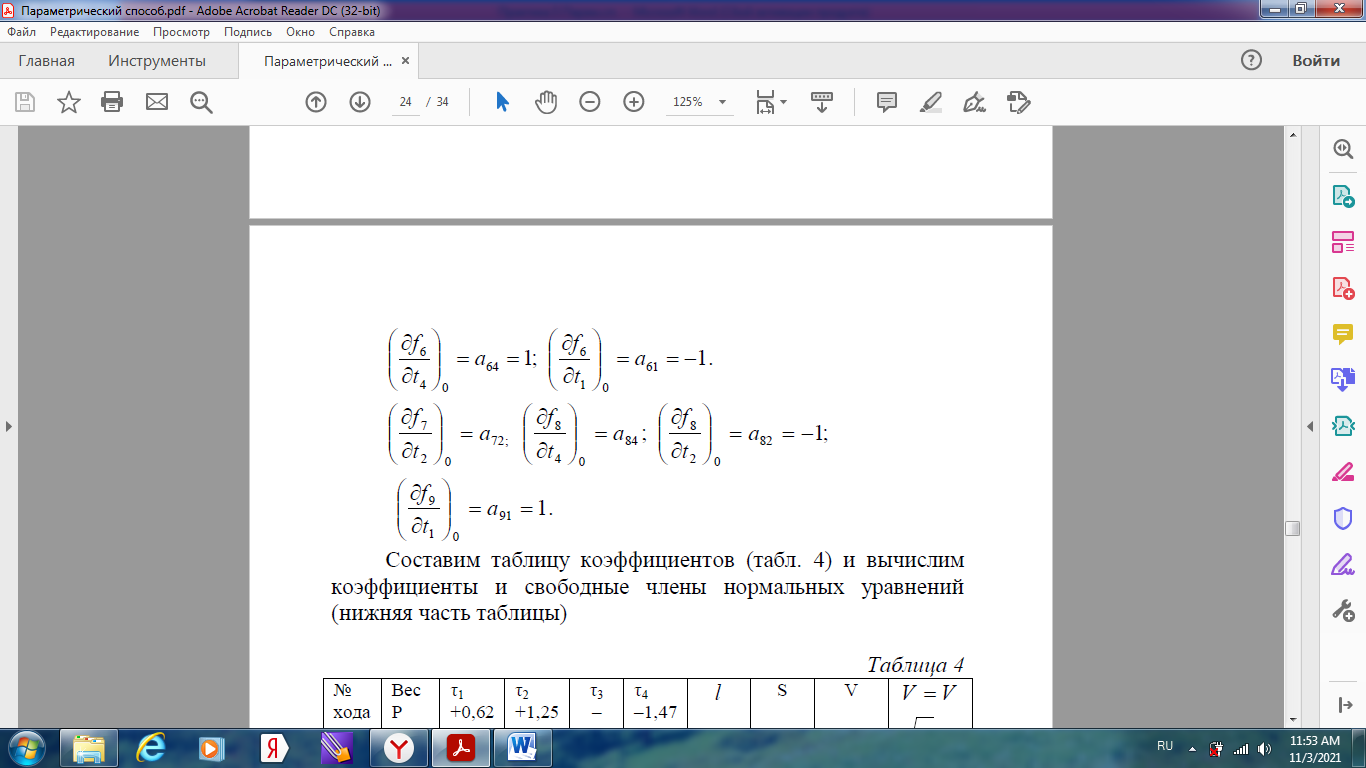 Составим таблицу коэффициентов (табл. 4) нормальных уравнений 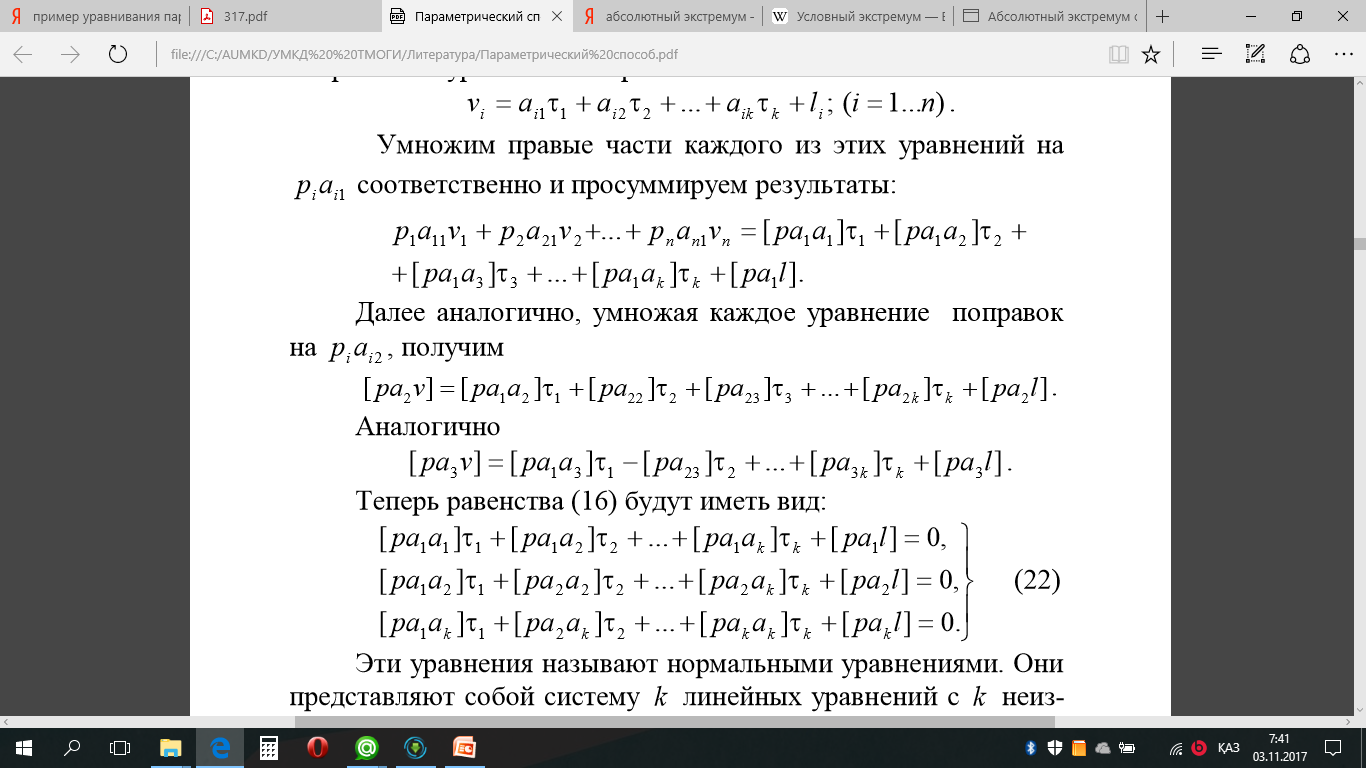 и вычислим коэффициенты и свободные члены нормальных уравнений (нижняя часть таблицы). 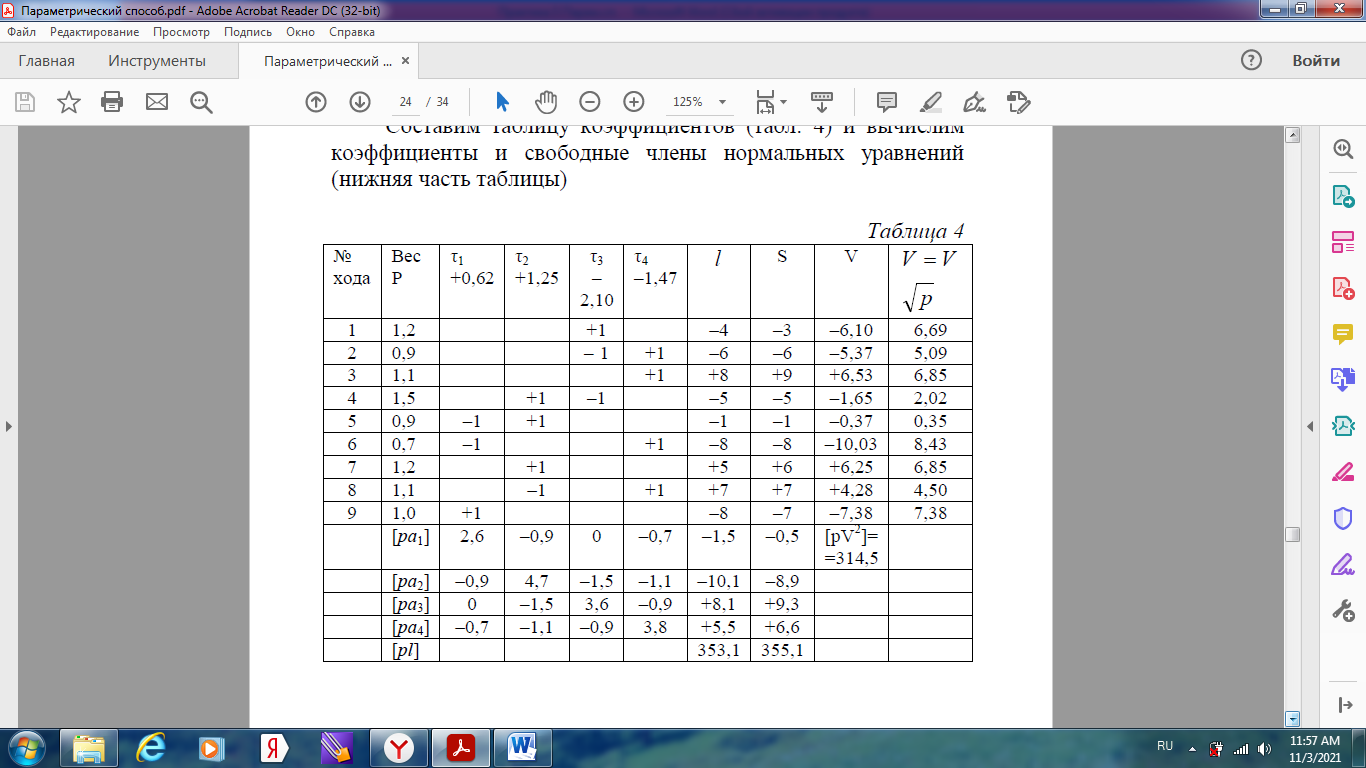 Решение нормальных уравнений выполняется через онлайн калькулятор по схеме Гаусса https://matworld.ru/calculator/gauss-method-online.php  Из решения нормальных уравнений находим поправки τ в приближенные значения параметров и вычисляем уравненные значения параметров. Затем вычисляем поправки в измеренные превышения. 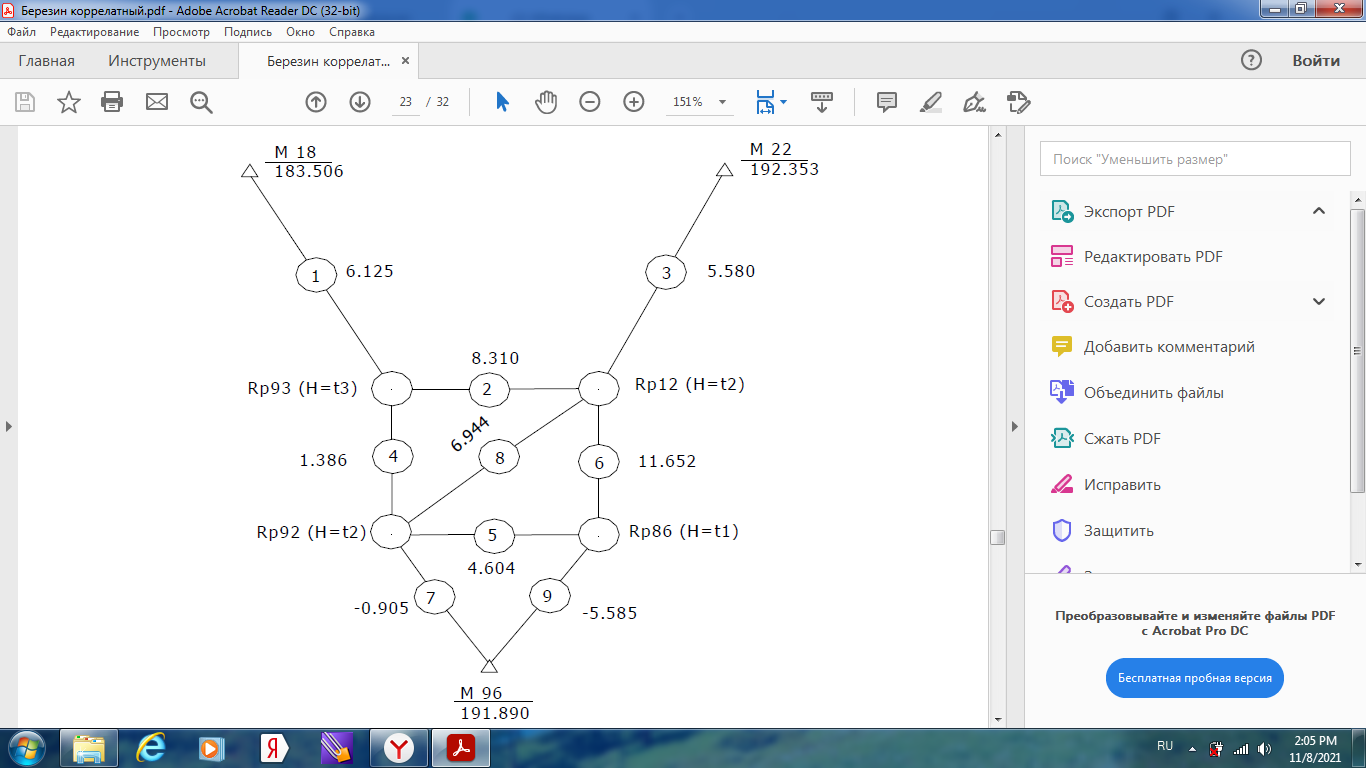 |
