Введение. Введение понятие определителя

Название	Введение понятие определителя
Дата	19.04.2021
Размер	465 Kb.
Формат файла
Имя файла	Введение.doc
Тип	Реферат #196215

Содержание:
Введение ……………………………………………….……..…………...………2

1. Понятие определителя……………………….…..………………..…………...3

1.1 Определители второго порядка….…………..…………………….3 – 5

1.2 Определители третьего порядка……………..………………………..5

1.3 Определители n –го порядка……………………..……………………6

2. Значение определителя………………………………………………………...7

2.1 Основные свойства определителей……………………...………7 – 11

3. Применение………………………………………………………………11 – 12

4. Определители в аналитической геометрии…………….………………...….13

5. Связь определителей с матрицами…………………………………………..13

6. Якобиан………………………………………………………………………..14

Заключение………………………………………………………………………15

Список используемой литературы……………………………………………..16

Введение

Определители впервые были введены для решения системы уравнений первой степени. В 1750 году швейцарский математик Г. Крамер дал общие формулы, выражающие неизвестные через Определители, составленные из коэффициентов системы. Примерно через сто лет теория определителей, выйдя далеко за пределы алгебры, стала применяться во всех математических науках.

В настоящем реферате рассмотрены определители второго и третьего порядка, приведены примеры решения систем уравнений методом определителей.

1. Понятие определителя

Определитель (детерминант), – в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число («значение» определителя). Очень часто под понятием «определитель» имеют в виду, как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе.

1.1 Определители второго порядка

Рассмотрим систему уравнений:

a1x + b1y = с1

a2x + b2y = с2

Данную систему можно решить традиционными методами - подстановки и сложения уравнений. Однако в ряде случаев оказывается легче применить определители.

Представим систему в виде квадратной матрицы:

| a1 b1 |

А = | |

| a2b2 | .

число а1b1– а2b2 называют определителем системы и обозначают detA или D

| a1 b1 | | a1 b1 |

Dx = | | , Dy = | |

| a2 b2 | | a2 b2 |

Определитель Dx получается из D заменой элементов первого столбца свободными членами системы; аналогично Dy.

Возможны три случая:

Случай 1: определитель системы не равен нулю: D ¹ 0. Тогда система имеет единственное решение: x = Dx/D , y= Dy/D.

Случай 2: определитель системы равен нулю: D = 0 (т.е. коэффициенты при неизвестных пропорциональны). Пусть при этом один из определителей Dx, Dy не равен нулю (т.е. свободные члены не пропорциональны коэффициентам при неизвестных). В этом случае системы не имеет решений.

Случай 3: D = 0, D x = 0, D y = 0 (т.е. коэффициенты и свободные члены пропорциональны). Тогда одно из уравнений есть следствие другого: система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.

Рассмотрим несколько примеров решения систем двух уравнений с двумя неизвестными методом определителей.

Пример 1. Решить систему уравнений:

2x + 3y = 8

7x - 5y = -3

| 2 3 | | 8 3| | 2 8 |

D= | | = -31 Dx = | | = -31 Dy = | | = - 62

| 7 -5 | | -3 -5| | 7 -3 |

Система имеет единственное решение.

х = Dx/D =1 y = Dy/D = 2

Пример 2. Решить систему уравнений:

2x + 3y = 8

4x + 6y = 10

| 2 3 | | 8 3|

D = | | = 0, при этом Dx = | |= 18 ¹ 0. | |

| 4 6 | | 10 6 |

Коэффициенты пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.

Пример 3. Решить систему уравнений:

2x + 3y = 8

4x +6y = 10

| 2 3 | | 8 3 | | 2 8 |

D = | |= 0 Dx = | | =0 Dy = | | =0

| 4 6 | | 16 6 | | 4 16 |

Одно из уравнений есть следствие другого (например, второе получается из первого, умножая на два). Система сводится к одному уравнению и имеет бесчисленное множество решений.

1.2 Определители третьего порядка

Решение систем из трех линейных уравнений с тремя неизвестными также можно решить методом определителей. Определителем квадратной матрицы третьего порядка | a1b1c1 | называется выражение D = а1b2c3 – a1b3c2 + b1c2a3 – А= | a2 b2 c2 | b1c3a2 + c1a2b3 – c1a3b2| a3 b3 c3 | или, если выразить его через определители 2-го порядка:

| b2 c2| | a2 c2 | | a2 b2 |

a1 | | - b1 | | + c1 | |

| b3 c3| | a3 c3 | | a3 b3|

1.3 Определители n –го порядка

Определителем квадратной матрицы n-го порядка А, где

| a11 a12 …a1n | | a22 a23…a2n |

| a21 a22 … a2n | называют число D = a11 | …………… | -

A = | ………………… | | an2 an3…annn|

| an1 an2 … ann |

| a21 a23…a2n | | a21 a22…a2(n-1)|

- a12 | ………….. | +…+ (-1)n+1a1n | ……………. |

| an1 an3…ann | | an1 an2…an(n-1) |

То есть мы имеем знакочередующуюся сумму произведений, в которых один из из множителей – элемент первой строки, а другой – определитель матрицы (n-1)-го порядка, полученной вычеркиванием той строки и того столбца которым принадлежит первый множитель.

Например:

| 4 1 3 5 |

| 2 3 2 1 | | 3 2 1 | | 2 2 1 | | 2 3 1 | | 2 3 2 |

| 5 2 1 4 | = 4 | 2 1 4 | - 1 | 5 1 4 | + 3 | 5 2 4 | - 5 | 5 2 1 |

| 11 6 5 10| | 6 5 10| | 11 5 10 | |11 6 10 | | 11 6 5 |

= 4( 3(10-20) – 2(20-24) + 1(10-6)) – 1( 2(10-20) –2(50-44) + 1(25-11)) +

+ 3( 2(20-24) – 3(50-44) + 1(30-22)) –5( 2(10-6) – 3(25-11) +2(30-22)) = -28

2. Значение определителя

Под значением определителя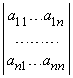

принято понимать сумму всех произведений из n элементов, т.е.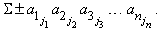

В этой формуле суммирование ведется по всем перестановкам j₁, ј, j_n чисел 1, 2, ј, n и перед членом ставится знак плюс, если перестановка четна, и минус, если эта перестановка нечетна. Такая сумма насчитывает ровно n! членов, половина которых берется со знаком плюс, половина – со знаком минус.

Каждый член суммы содержит по одному члену из каждого столбца и каждой строки определителя. Можно доказать, что эта сумма совпадает с выражением, получаемым при разложении определителя по минорам.

2.1 Основные свойства определителей

Все свойства определителя следуют из определения определителя и свойств конечных сумм, приводятся без общих доказательств с демонстрацией на примере определителей 2-го и 3-го порядков.

Свойство 1. Равноправность строк и столбцов. Определитель не меняет своего значения при замене всех его строк соответствующими столбцами

Т.е.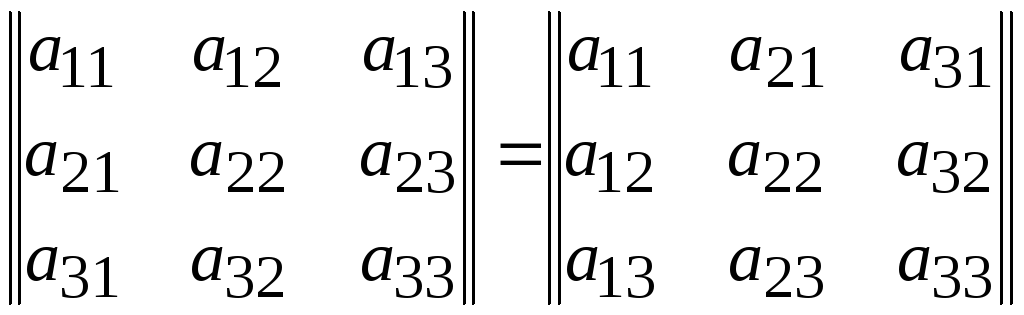

.

Для доказательства этого свойства достаточно вычислить определители в левой и правой частях равенства и убедиться в равенстве полученных при этом членов. В связи с этим свойством в дальнейшем вместо слов «строка» или «столбец» будем говорить просто «ряд», подразумевая их равноправность.

Свойство 2. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на противоположный

Пример: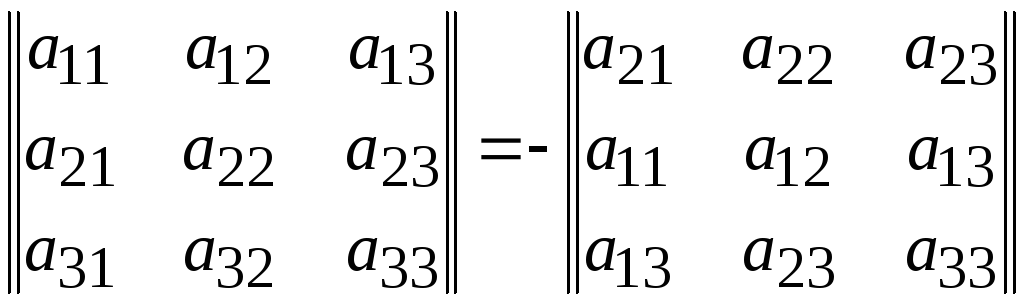

.

Для доказательства этого свойства достаточно вычислить по правилу треугольника определители, стоящие в правой и левой частях равенства.

Следствие 1: Определитель с двумя одинаковыми рядами равен нулю.

Действительно, при перестановке двух одинаковых рядов абсолютное значение определителя не изменится, а, с другой стороны, в силу свойства 2 изменит знак на противоположный, т.е.

, значит

, следовательно,

.

Следствие 2. Сумма произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.

Действительно, все такие разложения представляют из себя определители, содержащие два одинаковых ряда:

Свойство 3. Общий множитель элементов какого-либо ряда можно выносить за знак определителя.

Действительно, поскольку определитель можно вычислить, раскладывая его по элементам строки (столбца), вычислим определитель, раскладывая его по элементам строки, умноженной на число

, тогда каждое слагаемое будет содержать множитель

, который может быть вынесен за скобку.

Следствие 1. Если все элементы какого-либо ряда равны нулю, то определитель равен нулю.

Следствие 2. Если все элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда, то определитель равен нулю.

Действительно,

Свойство 4. Линейное свойство определителя. Если в определителе

-го порядка некоторая

-ая строка представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей. Первый определитель будет иметь в

-ой строке первые из упомянутых слагаемых , элементы в остальных строках будут такими же, как и в исходном определителе, а второй определитель в

-ой строке будет иметь вторые из упомянутых слагаемых, а остальные строки будут совпадать с исходным определителем, т.е.

.

Это свойство следует из определения определителя, если разложить его по элементам

-ой строки, а затем воспользоваться распределительным законом суммы.

Определение. Элементарными преобразованиями матрицы называются следующие преобразования:

1) умножение строки (столбца) на число отличное от нуля;

2) прибавление к одной строке (столбцу) другой строки (столбца);

3) перестановка строк (столбцов).

Свойство 5. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель

, то величина определителя не изменится.

Свойство 6. Определитель треугольной матрицы равен произведению диагональных элементов.

.

нижний треугольный верхний треугольный

определитель определитель

Определение. Минором -ого порядка матрицы

называется детерминант матрицы порядка

, образованный элементами, стоящими на пересечении выбранных

строк и столбцов. Каждая матрица имеет столько миноров данного порядка, сколькими способами можно выбрать номера строк и столбцов. Если матрица

квадратная, то каждому минору –огопорядка сопоставляется дополнительный минор, который по определению есть определитель матрицы порядка ( ), составленный из элементов, оставшихся после вычеркивания строк и столбцов.

3. Применения

Решение системы уравнений

можно получить, если первое уравнение умножить на b₂, второе – на b₁, а затем вычесть одно уравнение из другого. Проделав эти операции, мы получим

или, если

то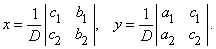

Такая запись решения с помощью определителей допускает обобщение на случай решения системы n линейных уравнений с n неизвестными; каждый определитель будет n-го порядка. Определителем системы линейных уравнений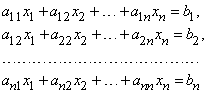

будет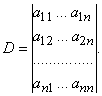

Заметим, что если D = 0, то уравнения либо несовместны, либо не являются независимыми. Поэтому предварительное вычисление определителя D позволяет проверить, разрешима ли система линейных уравнений.

4. Определители в аналитической геометрии

Общее уравнение конического сечения представимо в виде

Определитель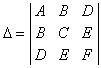

называется дискриминантом. Если D = 0, то кривая вырождается в пару параллельных или пересекающихся прямых либо в точку.

Другой пример: площадь треугольника A с вершинами в точках (обход – против часовой стрелки) (x₁, y₁), (x₂, y₂) и (x₃, y₃) определяется выражением

5. Связь определителей с матрицами

Матрицей называется запись массива чисел в виде прямоугольной таблицы. Определители связаны с квадратными матрицами; например, определитель матрицы

Если A, B и С – квадратные матрицы и

, то |A|Ч|B| = |C|.

6. Якобиан

Если x = f (u, v), y = g (u, v) – преобразование координат, то определитель

называется якобианом или определителем Якоби этого преобразования. Если J № 0 в некоторой точке, то в ее окрестности уравнения преобразования можно однозначно разрешить относительно u и v, представив их как функции от x и y.

Заключение

В процессе работы над рефератом я пользовалась научной литературой, сопоставляла и сравнивала различные точки зрения, выделяла главное. В работе рассмотрены понятие определителя, его значение, а также подробно рассмотрены определители второго и третьего порядков, часто встречающиеся на практике. Для определителя третьего порядка приводятся два способа вычисления.

Определитель (детерминант), – в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число («значение» определителя). Очень часто под понятием «определитель» имеют в виду, как значение определителя, так и форму его записи. Определители позволяют удобно записывать сложные выражения, возникающие, например, при решении линейных уравнений в аналитической геометрии и в математическом анализе

Список используемой литературы

Кузнецов, Б.Т. Математика : учебник / Б.Т. Кузнецов. - 2-е изд., перераб. и доп. - Москва : Юнити-Дана, 2015. - 719 с. : ил., табл., граф. - (Высшее профессиональное образование: Экономика и управление). - Библиогр. в кн. - ISBN 5-238-00754-Х ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=114717 (17.06.2019).
Балдин, К.В. Высшая математика : учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рокосуев ; под общ. ред. К.В. Балдина. - 2-е изд., стер. - Москва : Издательство «Флинта», 2016. - 361 с. : табл., граф., схем. - Библиогр. в кн. - ISBN 978-5-9765-0299-4 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=79497 (17.06.2019).
Краткий курс высшей математики : учебник / К.В. Балдин, Ф.К. Балдин, В.И. Джеффаль и др. ; под общ. ред. К.В. Балдина. - 2-е изд. - Москва : Издательско-торговая корпорация «Дашков и К°», 2017. - 512 с. : табл., граф., схем., ил. - Библиогр. в кн. - ISBN 978-5-394-02103-9 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=450751 (17.06.2019).
Тыртышников, Е.Е. Основы алгебры : учебник / Е.Е. Тыртышников. - Москва : Физматлит, 2017. - 464 с. - Библиогр.: с. 449-450. - ISBN 978-5-9221-1728-9 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=485535 (17.06.2019).
Высшая математика для экономистов : учебник / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман ; ред. Н.Ш. Кремер. - 3-е изд. - Москва : Юнити-Дана, 2015. - 482 с. : граф. - («Золотой фонд российских учебников»). - ISBN 978-5-238-00991-9 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=114541 (17.06.2019).